随机过程基本概念
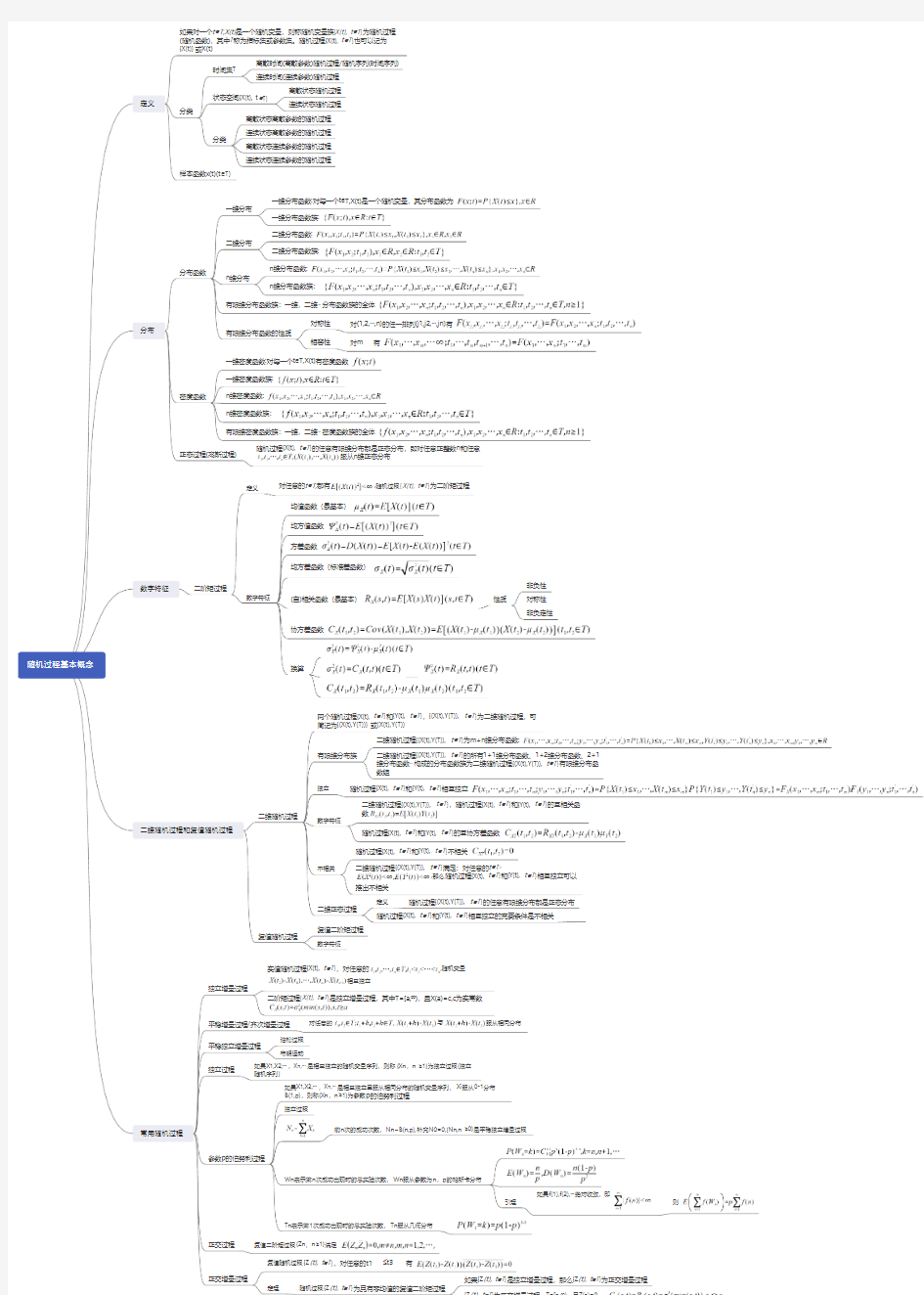
如果对一个t?T,X(t)是一个随机变量,则称随机变量族{X(t), t?T}为随机过程(随机函数),其中T称为指标集或参数集。随机过程{X(t), t?T}也可以记为
都有
,对任意的
相互独立
随机过程-答案
2012-2013学年第一学期统计10本 《随机过程》期中考试 一. 填空题 1.设马氏链的一步转移概率矩阵()ij P p =,n 步转移矩阵() ()n ij P p =,二者之间的关系为 (n) n P P = 2.状态i 常返的充要条件为( ) n i i n p ∞ ==∑∞。 3.在马氏链{},0n X n ≥中,记() n i j p ={}0,11,n P Xm j m n X j X i ≠≤≤-==,n ≥1. i j p =( ) 1n i j n p ∞ =∑,若i j p <1,称状态i 为 。 二. 判断题 1. S 是一个可数集,{:0n n X ≥}是取值于S 的一列随机变量,若 ( ) 1 01110011111 1,,...,(,...,)n n n n n n n n n n n n i i S P i X i X i X i P i i -+++--++-?≥?∈X =|====X =|X =并且满足,则{:0n n X ≥}是一个马氏链。 × 2. 任意状态都与它最终到达的状态是互通的,但不与它自己是互通的。 × 3. 一维与二维简单随机游动时常返的,则三维或更高维的简单随机游动也是常返的。× 4. 若状态i ?状态j ,则i 与j 具有相同的周期。 √ 5. 一个有限马尔科夫链中不可能所有的状态都是暂态。 √ 三. 简答题 1.什么是随机过程,随机序列? 答:设T 为[0,+∞)或(-∞,+∞),依赖于t(t ∈T)的一族随机变量(或随机向量){t ξ}通称为随机过程,t 称为时间。当T 为整数集或正整数集时,则一般称为随机序列。 2 .什么是时齐的独立增量过程?
随机过程试题带答案
1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为 。 2.设随机过程X(t)=Acos( t+),- 北京邮电大学2012——2013学年第1学期 《概率论与随机过程》期末考试试题答案 考试注意事项:学生必须将答题内容(包括填空题)做在试题答题纸上,做在试卷纸上一律无效。在答题纸上写上你的班号和选课单上的学号,班内序号! 一. 单项选择题和填空题:(每空3分,共30分) 1.设A 是定义在非空集合Ω上的集代数,则下面正确的是 .A (A )若A B ∈∈A,A ,则A B -∈A ; (B )若A A B ∈?A,,则B ∈A ; (C )若12n A n =∈?A,,,,则 1 n n A ∞=∈A ; (D )若12n A n =∈?A,,,,且123A A A ??? ,则 1 n n A ∞ =∈A . 2. 设(),ΩF 为一可测空间,P 为定义在其上的有限可加测度,则下面正确的是 .c (A )若A B ∈∈F,F ,则()()()P A B P A P B -=-; (B )若12n A n =∈?F,,,,,且123A A A ??? ,则1 li ( )()m n n n n P A A P ∞→∞ ==; (C )若A B C ∈∈∈F,F,F,,则()()()()P A B C P A P AB P A BC =++; (D )若12n A n =∈?F,,,,,且,i j A i j A =??=/,1 1 ( )()n n n n P P A A ∞ ∞===∑. 3.设f 为从概率空间(),P ΩF,到Borel 可测空间(),R B 上的实可测函数,表达式为100 0()k A k f kI ω==∑,其中1000 ,, i j n n i j A A A ==??=Ω/=,则fdP Ω=? ; 第十二章 平稳随机过程 §1 基本概念 定义1:已给s.p t X t X {=,}T t ∈,若1≥?n ,即T 中任意的,,,21n t t t Λ与 h t h t h t n +++,,,21Λ,n 维r.v ),,(21n t t t X X X Λ与),,(21h t h t h t n X X X +++Λ有相同 的n 维d.f 。即 ) ,,,;,,(),,() ,,(),,,;,,,(2121212121212121n n n h t h t h t n t t t n n x x x h t h t h t F x X x X x X P x X x X x X P x x x t t t F n n ΛΛΛΛΛΛ+++=≤≤≤=≤≤≤=+++ 则称s.p t X 是一个严(强,狭义)平稳过程。 当t X ?n 维d.l 时,则有 ),,;,,,(),,;,,,(21212121n n n n x x x h t h t h t f x x x t t t f ΛΛΛΛ+++= 若取n =1,则有),(),(1111x h t f x t f +=,特别,当T ∈0,可取,1t h -=则有),0(),(111x f x t f =。此时平稳过程t X 的一维d.l 与1t (时间)无关。于是 X X m dx x xf t X E μ=== ?+∞ ∞ -),0()(1 即t X 的均值是一个与时间无关的常数。 其方差 ?∞ ∞ -=-=-=.),0()(][2 22 X X X t t dx x f m x m X E X D σ也与时间t 无关的 常数。 而且T X 的二维d.l 也只依赖于.21t t -=τ即当2t h -=时,有 ).,;(),;0,(),;,(2121212121x x f x x t t f x x t t f τ∧ =-= 所以t X 与τ+t X 之间自相关为 ??∞∞-∞ ∞ -+== =+).(),;(),(21212 1ττττX t t X R dx dx x x f x x X X E t t R 它只依赖于.τ类似地τ+t t X X ,之间协方差为 第二章随机过程的基本概念 §1随机过程及其概率分布 、随机过程概念: 一、随机过程概念: 初等概率论所研究的随机现象,基本上可以用随机变量或随机向量来描述.但在实际中有些随机现象要涉及(可列或非可列)无穷多个随机变量. 例1.某人扔一枚硬币,无限制的重复地扔下去,要表示无限多次扔的结果,我们不妨记正面为1,反面为0.第次扔的结果是一个,其分布,无限多次扔n n r vX ?{}{}1012n n P X P X ====,无限制的重复地扔,要表示无限多次扔的结果,我们不妨反面为其分布无限多次扔的结果是一个随机过程,可用一族相互独 立,,或表示.r v ?1X ,2X {},1n X n ≥ n n X 0n n 0 1 2 3 4 5 6 7 8 910 …… 例2.当固定时,电话交换站在时间内来到的呼叫次数是,记, ,其中是单位时间内平均来到的呼叫次数,而,若从变到,时刻来到的呼叫次数需用一族随机变量表 它为非降的阶,在有呼唤来到的时刻阶跃地增加,假定在任一呼唤来到的时刻不可能来到多)(0)t t ≥[0,] t r v ?()X t ()()X t P t λ λ0λ>t 0∞t {}(),[0,)X t t ∈∞()X t ,电话交换站在记,若时刻示, 是一个随机过程. 对电话交换站作一次观察可得到一条表示以前来到的呼唤曲线,它为非降的阶梯曲线,在有呼唤来到的时刻阶跃地增加,(假定在任一呼唤来到的时刻不可能来到多于一次呼唤). E t 1()x t 同理,第二次观察,得到另一条阶梯形曲线; 同理,第n 次观察,得到另一条阶梯形曲线. 2()x t ()n x t ,第二次观察,得到另一条阶梯形曲,第,得到另一条阶梯形曲 总之,一次试验得到阶梯形曲线形状具有随机性 第二章 随机过程分析 学习指导 1.1.1 要点 随机过程分析的要点主要包括随机过程的概念、分布函数、概率密度函数、数字特征、通信系统中常见的几种重要随机过程的统计特性。 1. 随机过程的概念 随机过程是一类随时间作随机变化的过程,它不能用确切的时间函数描述。可从两种不同角度理解:对应不同随机试验结果的时间过程的集合,随机过程是随机变量概念的延伸。 2. 随机过程的分布函数和概率密度函数 如果ξ(t )是一个随机过程,则其在时刻t 1取值ξ(t 1)是一个随机变量。ξ(t 1)小于或等于某一数值x 1的概率为P [ ξ(t 1) ≤ x 1 ],随机过程ξ(t )的一维分布函数为 F 1(x 1, t 1) = P [ξ(t 1) ≤ x 1] (2-1) 如果F 1(x 1, t 1)的偏导数存在,则ξ(t )的一维概率密度函数为 1111111 (,) (, ) (2 - 2)?=?F x t f x t x 对于任意时刻t 1和t 2,把ξ(t 1) ≤ x 1和ξ(t 2) ≤ x 2同时成立的概率 {}212121122(, ; , )(), () (2 - 3)F x x t t P t x t x ξξ=≤≤ 称为随机过程 (t )的二维分布函数。如果 2212122121212 (,;,) (,;,) (2 - 4)F x x t t f x x t t x x ?=??? 存在,则称f 2(x 1, x 2; t 1, t 2)为随机过程 (t )的二维概率密度函数。 对于任意时刻t 1,t 2,…,t n ,把 {}n 12n 12n 1122n n ()(),(),,() (2 - 5) =≤≤≤L L L F x x x t t t P t x t x t x ξξξ,,,;,,,称为随机过程 (t )的n 维分布函数。如果 n n 12n 12n n 12n 12n 12n (x )() (2 - 6)?=???L L L L L F x x t t t f x x x t t t x x x ,,,;,,,,,,;,,, 存在,则称f n (x 1, x 2, …, x n ; t 1, t 2, …, t n )为随机过程 (t )的n 维概率密度函数。 3. 随机过程的数字特征 随机过程的数字特征主要包括均值、方差、自相关函数、协方差函数和互相关函数。 随机过程 (t )在任意给定时刻t 的取值 (t )是一个随机变量,其均值为 []1()(, )d (2 - 7)E t xf x t x ξ∞ -∞ =? 《随机过程期末考试卷》 1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为 。 2.设随机过程X(t)=Acos( t+),- 平稳随机过程 ?严格平稳随机过程 ?广义平稳随机过程 ?平稳随机过程自相关函数性质?各态历经过程 1. 严格平稳(Strict Sense Stationary, SSS)随机过程定义: 随机过程X (t )的任意N 维统计特性与时间起点无关。 1111(,,,,,)(,,,,,) X N N X N N p x x t t t t p x x t t +?+?=如果X (t ) 是严格平稳的,则与t 无关。 (,)()X X p x t p x =即X(t)与X(t+?t)具有相同的统计特性。 二维概率密度 只依赖于τ,与t 1和t 2的具体取值无关。 12121212121221212 (,,,)(,,,) (,,,0)(,,) X X X X p x x t t p x x t t t t p x x t t t t p x x t t =+?+?=-?=-=ττ=- 如果X (t )是严格平稳随机过程, 则 121212121212 (,)(,,,)() X X X R t t x x p x x t t dx dx R t t ∞ -∞ ==ττ=-?()()X X X m t xp x dx m ∞ -∞==?22 2()()()X X X X t x m p x dx ∞ -∞σ=-=σ ? 100200300400500 -4-3-2-101234Stationay Gaussian Noise 0100200300400500 -4 -3 -2-101234Non-stationay Gaussian Noise 第一章 随机过程的基本概念 1.设随机过程 +∞<<-∞=t t X t X ,cos )(0ω,其中0ω是正常数,而X 是标准正态变量。试求X (t )的一维概率分布 解:∵ 当0cos 0=t ω 即 πω)21(0+ =k t 即 πω)2 1 (10+=k t 时 {}10)(==t x p 若 0c o s 0≠t ω 即 πω)2 1 (1 0+≠ k t 时 当 0c o s 0>t ω时 ξπ ωωξd e t x X P t x F t x ? - = ??? ? ??≤=02cos 0 2 021cos ),( 此时 ()t e x t x F t x f t x 0c o s 2c o s 1 21,),(022ωπ ω? =??=- 若 0c o s 0 ?? ?= ,2 ,cos )(出现反面出现正面t t t X π 假定“出现正面”和“出现反面”的概率各为21。试确定)(t X 的一维分布函数)2 1 ,(x F 和)1,(x F ,以及二维分布函数)1,2 1;,(21x x F 解:(1)先求)21,(x F 显然?? ?=?????=??? ??出现反面出现正面 出现反面出现正面10,2 1*2,2cos 21π X 随机变量?? ? ??21X 的可能取值只有0,1两种可能,于是 21 021= ??????=?? ? ??X P 2 1121=??????=??? ??X P 所以 再求F (x ,1) 显然?? ?-=?? ?=出现反面出现正面出现反面出现正面 2 1 2 cos (1)πX {}{}2 1 2)1(-1(1)====X p X p 所以 ???? ???≥<≤<=2 121- 2 1-1 0,1)(x x x x F (2) 计算)1,2 1 ;,(21x x F ?? ?-=?? ?=出现反面出现正面 出现反面出现正面 2 1)1(, 1 0)2 1( X X ?????≥<≤<=??? ?? 11 102 1 00 21,x x x x F 北京工业大学2009-20010学年第一学期期末 数理统计与随机过程(研) 课程试卷 学号 姓名 成绩 注意:试卷共七道大题,请写明详细解题过程。 考试方式:半开卷,考试时只允许看教材《概率论与数理统计》 浙江大学 盛 骤等编第三版(或第二版)高等教育出版社。可以看笔记、作业,但不允许看其它任何打印或复印的资料。考试时允许使用计算器。考试时间120分钟。考试日期:2009年12月31日 一、随机抽取某班28名学生的英语考试成绩,算得平均分数为80=x 分,样本标准差8=s 分,若全年级的英语成绩服从正态分布,且平均成绩为85分,问:能否认为该班的英语成绩与全年级学生的英语平均成绩有显著差异(取显著性水平050.=α)? 解:这是单个正态总体 ),(~2σμN X ,方差2σ未知时关于均值μ的假设检验问题,用T 检验法. 解 85:0=μH ,85:1≠μH 选统计量 n s x T /0 μ-= 已知80=x ,8=s ,n =28,850=μ, 计算得n s x T /0μ-= 31 .328/885 80=-= 查t 分布表,05.0=α,自由度27,临界值052.2)27(025.0=t . 由于052.2>T 2622.2>,故拒绝 0H ,即在显著水平05.0=α下不能认为 该班的英语成绩为85分. 050.= 解:由极大似然估计得.2?==x λ 在X 服从泊松分布的假设下,X 的所有可能的取值对应分成两两不相交的子集A 0, A 1,…, A 8。 则}{k X P =有估计 =i p ?ΛΛ,7,0, !2}{?2 ===-k k e k X P k =0?p 2016随机过程(A )解答 1、(15分)设随机过程V t U t X +?=)(,),0(∞∈t ,U ,V 是相互独立服从正态分布(2,9)N 的随机变量。 1) 求)(t X 的一维概率密度函数; 2) 求)(t X 的均值函数、相关函数和协方差函数。 3) 求)(t X 的二维概率密度函数; 解: 由于U ,V 是相互独立服从正态分布(2,9)N 的随机变量,所以V t U t X +?=)(也服从正态分布, 且: {}{}{}{}()()22m t E X t E U t V t E U E V t ==?+=?+=+ {}{}{}{}22()()99D t D X t D U t V t D U D V t ==?+=+=+ 故: (1) )(t X 的一维概率密度函数为:()2 22218(1) (),x t t t f x e x --- += -∞≤≤∞ (2) )(t X 的均值函数为:()22m t t =+;相关函数为: {}{} (,)()()()()R s t E X s X t E U s V U t V =?=?+??+ {}{}{} 22()13()413 st E U s t E U V E V st s t =?++??+=?++?+ 协方差函数为:(,)(,)()()99B s t R s t m s m t st =-?=+ (3)相关系数: (,)s t ρρ== == )(t X 的二维概率密度函数为: 2212222(22)(22)12(1)9(1)4(1),12(,)x s x t s t s t f x x e ρ????-----?? +????-++???????? = 2、(12分)某商店8时开始营业,在8时顾客平均到达率为每小时4人,在12时顾客的 平均到达率线性增长到最高峰每小时80人,从12时到15时顾客平均到达率维持不变为每小时80人。问在10:00—14:00之间无顾客到达商店的概率是多少?在10:00—14:00之间到达商店顾客数的数学期望和方差是多少? 解: 到达商店顾客数服从非齐次泊松过程。 将8时至15时平移到0—7时,则顾客的到达速率函数为: 419,04 ()80,47t t t t λ+≤≤?=? <≤? 在10:00—14:00之间到达商店顾客数(6)(2)X X -服从泊松分布,其均值: 6 4 6 2 2 4 (6)(2)()(419)80282m m t dt t dt dt λ-==++=??? 平稳随机过程及其数字特征 平稳随机过程 粗略的说——随机过程的统计特征不随时间的推移而变化。一.严平稳随机过程 1. 定义设有随机过程{ X(t) , t ∈T},若对于任意n 和任意t1 因此:严平稳过程的二维数字特征仅是(时间差τ)的函数 综上所述:要按上述严平稳过程的定义来判断一个过程是否平稳?是很困难的。 a):一般在实用中,只要产生随机过程的主要物理条件,在时间 进程中不变化。则此过程就可以认为是平稳的。 例如:在电子管中由器件的颗粒效应引起的“散弹噪声”,由于产生此噪声的主要物理条件与时间无关,所以此噪声可以认为是平稳过程。 12121212 12 1 21212 2 2 2 (,)(,;)() (,)()()(,;)()()(0)(0)[()] X X X X X X X X X X X X X X R t t x x f x x dx dx R C t t x m x m f x x dx dx C R m C R m D X t τττττσ=?==??==?=?==∫∫∫∫ ∞<)]([2 t X E b):另一方面,对有些非平稳过程,可以根据需要,如果它在所观测的时间段内是平稳的,就可以视作这一时间段上的平稳过程来处理。即在观测的有限时间段内,认为是平稳过程。 因此,工程中平稳过程的定义如下: 二、宽平稳过程1、定义 若二阶矩过程( )X(t) 满足: E[X(t)]=m x ←常数 R x (t 1,t 2)=R x (τ) ←只与时间间隔(τ=t 2-t 1)有关 则称过程X(t)为“宽平稳随机过程”(广义平稳过程)。 可见:一个均方值有限的严平稳过程,一定是宽平稳过程。反之:一个宽平稳过程,则不一定是严平稳过程。 c):一般在工程中,通常只在相关理论的范围内讨论过程的平稳问题。即:讨论与过程的一、二阶矩有关的问题。 ! 第一章 随机过程基本概念 P39 1. 设随机过程()0cos X t X t ω=,t -∞<<+∞,其中0ω是正常数,而X 是标准正态变量。试求()X t 的一维概率分布。 解: 1 当0cos 0t ω=,02 t k π ωπ=+ ,即0112t k πω??= + ??? (k z ∈)时, ()0X t ≡,则(){}01P X t ==. 2 当0cos 0t ω≠,02 t k π ωπ≠+ ,即0112t k πω?? ≠ + ??? (k z ∈)时, ()~01X N ,,()0E X ∴=,()1D X =. ¥ ()[]()00cos cos 0E X t E X t E X t ωω===????. ()[]()22 000cos cos cos D X t D X t D X t t ωωω===????. ()()20~0cos X t N t ω∴,. 则( )2202cos x t f x t ω- = ;. 2. 利用投掷一枚硬币的试验,定义随机过程为 ()cos 2t X t t π?=??,出现正面,出现反面 假定“出现正面”和“出现反面”的概率各为 12。试确定()X t 的一维分布函数12F x ?? ???;和()1F x ;,以及二维分布函数12112 F x x ? ? ?? ? ,;, 。 】 解: 00 11101222 11 【第一章】 1.1 证明: ∵1111,,,,,A F F F F ∈ΩΦ∈ΩΩ∈Φ∈Ω-Φ∈ΩΦ∈U 且∴1F 是事件域。 ∵222,,,,c A A F F A F A A ∈Ω∈Ω∈-Φ∈=Ω- ∴22222,,,,c c A F A F A F A F A F ∈-Φ∈-Φ∈Ω-∈Ω-∈ 且2,c c A A A A F ΦΩ=ΩΦΩ∈U U U U U U ∴2F 是事件域。且12F F ∈。∵2ΩΩ∈∴3F Ω∈ ∴3F 是事件域。且23F F ∈∴123,,F F F 皆为事件域且123F F F ∈∈。 1.2 一次投掷三颗均匀骰子可能出现的点数ω为 (),,,,,,,,16,6,6i j k i R j R k R j i k j i j k ∈∈∈≥≥≤≤≤≤ ∴样本空间()6 1= ,,n i j i k j i j k ==≥≥ΩU 事件(){} ,,|,,i j k A i j k ωω==,,,,,,6,16,6i R j R k R j i k j i j k ∈∈∈≥≥≤≤≤≤ 事件域2F Ω= 概率测度 ()()() ,,1P 677i j k A i j = --,,,,,,16,6,6i R j R k R j i k j i j k ∈∈∈≥≥≤≤≤≤ 则(),,F P Ω为所求的概率空间。 1.3 证明: (1)由公理可知()0P Φ= (2)有概率测度的可列可加性可得 ()11 n n k k k k P A P A ==??= ???∑∑ (3)∵,,A B F A B ∈? ∴B A F -∈,()A B A -=Φ 由概率测度的可列可加性可得:()()()()P B P A B A P A P B A =+-=+- 即()()()P B A P B P A -=- 有概率测度的非负性可得()()()0P B P A P B A -=-≥,即()()P B P A ≥ (4)若B =Ω,由(3)则有() ()1P A P A =- (5) ∵()()()()121212P A A P A P A P A A +=+- 假设 ()()()()()1 121 1111m m m k k i j i j k m k i j m i j k m k P A P A P A A P A A A P A A A +=≤<≤≤<<≤=??=-+-+- ???∑∑∑K K U 成 立,则 《概率论与随机过程》第一章习题答案 1. 写出下列随机试验的样本空间。 (1) 记录一个小班一次数学考试的平均分数(设以百分制记分)。 解: ? ??????=n n n n S 100 , ,1,0 ,其中n 为小班人数。 (2) 同时掷三颗骰子,记录三颗骰子点数之和。 解:{}18,,4,3 =S 。 (3) 10只产品中有3只是次品,每次从其中取一只(取出后不放回),直到将3只次品都取出,记录 抽取的次数。 解: {}10,,4,3 =S 。 (4) 生产产品直到得到10件正品,记录生产产品的总件数。 解: { } ,11,10=S 。 (5) 一个小组有A ,B ,C ,D ,E5个人,要选正副小组长各一人(一个人不能兼二个职务),观察选 举的结果。 解: {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中,AB 表示A 为正组长,B 为副组长,余类推。 (6) 甲乙二人下棋一局,观察棋赛的结果。 解: {}210,,e e e S =其中,0e 为和棋,1e 为甲胜,2e 为乙胜。 (7) 一口袋中有许多红色、白色、蓝色乒乓球,在其中任意取4只,观察它们具有哪几种颜色。 解: {}rwb wb rb rw b w r S ,,,,,,=其中,,,,b w r 分别表示红色、白色、蓝色。 (8) 对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次 品就停止检查,或检查4个产品就停止检查,记录检查的结果。 解: {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中,0为次品,1为正品。 (9) 有A ,B ,C 三只盒子,a ,b ,c 三只球,将三只球装入三只盒子中,使每只盒子装一只球,观察 装球的情况。 解: {}Ca Bb Ac Cc Ba Ab Cb Bc Aa Cb Ba Ac Ca Bc Ab Cc Bb Aa S ,,;,,;,,;,,;,,;,,=其中,Aa 表示球a 放 在盒子A 中,余者类推。 (10) 测量一汽车通过给定点的速度。 解:{}0>=v v S (11) 将一尺之棰折成三段,观察各段的长度。 解: (){}1,0,0,0,,=++>>>=z y x z y x z y x S 其中,z y x ,,分别表示第一段,第二段,第三段的 长度。# 2. 设A ,B ,C 为三事件,用A ,B ,C 的运算关系表示下列事件。 (1) A 发生,B 与C 不发生。 解:C A (2) A 与B 都发生,而C 不发生。 解: C AB (3) A ,B ,C 都发生。 解: ABC (4) A ,B ,C 中至少有一个发生。 解: C B A ?? (5) A ,B ,C 都不发生。 解: C B A (6) A ,B ,C 中至多于一个发生。 解: A C C A ?? (7) A ,B ,C 中至多于二个发生。 解: C B A ?? (8) A ,B ,C 中至少有二个发生。 解: CA BC AB ??. # 3. 设{ }10,2,1, =S ,{}4,3,2=A ,{}5,4,3=B ,{}7,6,5=C ,具体写出下列各等式 (1)B A 。 解: {}5=B A ; (2)B A ?。 解: { }10,9,8,7,6,5,4,3,1=?B A ; (3)B A 。 解:{}5,4,3,2=B A ; 2 0 — 1分布 P(X 1) P,P(X 0) q EX DX pq 二项分布 P(X k) C : EX np DX npq 泊松分布 P(X k) k! EX DX 均匀分布略 正态分布 N(a, 2) f(x) (X a)2 2 2 EX DX 第一章随机过程的基本概念与基本类型 一.随机变量及其分布 1 .随机变量X ,分布函数F(x) P(X X) 离散型随机变量 X 的概率分布用分布列 P k P(X x k )分布函数 F(x) P k 连续型随机变量 X 的概率分布用概率密度 f(x) 分布函数F(x) X f(t)dt 2. n 维随机变量 X (X 1,X 2, ,X n ) 其联合分布函数 F (X ) F (X 1,X 2, , X n ) P(X 1 X [ , X 2 X 2 , , X n X n ,) 离散型 联合分布列 连续型联合概率密度 3 .随机变量的数字特征 数学期望:离散型随机变量 X EX X k P k 连续型随机变量 X EX xf (x)dx 2 2 2 方差:DX E(X EX) EX (EX) 反映随机变量取值的离散程度 协方差(两个随机变量 X,Y ): B XY E[(X EX )(Y 相关系数(两个随机变量 X, Y ) : XY t _ ____________________________________ VDX v'DY 独立 不相关 5 ?常见随机变量的分布列或概率密度、期望、方差 B XY EY)] E(XY) EX EY 则称X,Y 不相关。 4 ?特征函数 g(t) E(e ItX ) 离散 g(t) e ItX k p k 连续 g(t) e ltx f (x)dx 重要性质:g(0) 1 , g(t) 1 , g( t) g(t) , g (0) EX k 河北科技大学2012——2013 学年第一学期 《应用随机过程》试卷(A ′) 学院 理学院 班级 姓名 学号 一.概念简答题(每题5分,共40分) 1. 什么是随机过程,随机序列? 2. 随机过程2{()(),,(,)}X t A t t T A N ?μσ=∈ 是否为正态过程,试求其有限维分布的协方差阵。 3. 设()X t 为二阶矩过程,2 12()12(,)t t X R t t e -- =,若()()()d Y t X t X t dt =+ ,试求12(,)Y R t t 。 4.设某设备的使用期限为10年,在前5年平均2.5年需要维修一次,后5年平均2年维修一次,试求在使用期限内只维修过一次的概率。 5. 已知平稳过程() X t的功率谱密度为 2 42 4 () 109 X w S w w w + = ++ ,试求其自相关函数 () X Rτ。 6.一书亭用邮寄订阅销售杂志,订阅的顾客数是强度为6的一个泊松过程,每 位顾客订阅1年,2年,3年的概率分别为111 ,, 236 ,彼此如何订阅是相互独立的, 每订阅一年,店主即获利5元,设() Y t是[0,)t时段内,店主从订阅中所获得总收入。试求: (1)[()] E Y t(即[0,)t时段内总收入的平均收入); (2)[()] D Y t。 7. 写出卡尔曼滤波的算法公式 8.写出ARMA(p,q)模型的定义 二.综合题(每题10分,共60分) 1.设二维随机变量(,) X Y的概率密度为(,) f x y= 2,01,01 0, x y x y --<<< 2随机过程的基本概念 §2.1 基本概念 随机过程是指一族随机变量 . 对随机过程的统计分析称为随机过程论 , 它是随机数学中的一个重要分支,产生于本世纪的初期 . 其研究对象是随机现象 ,而它特别研究的是随“ 时间” 变化的“ 动态” 的随机现象 . 一随机过程的定义 1 定义设 E 为随机试验, S 为其样本空间,如果 (1对于每个参数 t ∈ T , X(e,t为建立在 S 上的随机变量, (2对每一个 e ∈ S , X(e,t为 t 的函数,那么称随机变量族 {X(e,t, t∈ T, e∈ S}为一个随机过程,简记为 {X(e,t, t∈ T}或 X(t。 ((((({} {} [](为随机序列。时,通常称 , 取可列集合当可以为无穷。 通常有三种形式: 参数一般表示时间或空间, 或有时也简写为一个轨道。 随机过程的一个实现或过程的样本函数,或称随机的一般函数,通常称为为对于 :上的二元单值函数。 为即若用映射来表示注意: t X T T T b a b a T T T T t X t X t e X T t e X S e S T t e X R S T t e X t 21321, , , , 3, 2, 1, 0, 1, 2, 3, , 3, 2, 1, 0T , . 4, . 3, , 2, :, . 1=---==??×?′?′L L L 为一个随机过程。则令 掷一均匀硬币, 例 , ( (cos (}, {1 t e X t X R t T e t H e t t X T H S =??íì====p2 随机过程举例 例 2:用 X(t表示电话交换台在 (0, t 时间内接到的呼唤的次数 , 则 (1对于固定的时刻 t, X(t为随机变量 , 其样本空间为{0, 1, 2, …..}, 且对于不同的 t, 是不同的随机变量 . (2对于固定的样本点 n, X(t=n是一个 t 的函数 . (即:在多长时间内来 n 个人 ? 所以 {X(t,t>0}为一个随机过程 . 相位正弦波。为随机过程,称为随机则令例 ( 一.填空题(每空2分,共20分) 1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为it (e -1) e λ。 2.设随机过程X(t)=Acos( t+),- 随机过程测试题二答案 1.以1T 表示泊松过程}0),({≥t t N 中事件首次发生的时刻,则对于t s ≤,求条件概率}1)(|{1=≤t N s T P 解: ==≤}1)(|{1t N s T P t s .(细节请查书) (5分) 2.设{N (t ), t ≥0}是强度为λ的泊松过程,N (t )表示到时刻t 为止事件A 发生的次数,则对任意t s <≤0,求),(),(t DN t EN )).(),(cov(s N t N 解:t t DN t EN λ==)()(; (5分) .))(),(cov())(),(-)(cov())(),(cov(s s N s N s N s N t N s N t N λ=+= (5分) 3.设某公交车站从早晨5时至晚上21时有车发出.从5时至8时乘客的平均到达率呈现性增加,5时乘客的平均到达率为200人/小时,8时乘客的平均到达率为1400人/小时;8时至18时乘客的平均到达率不变;18时至21时乘客的平均到达率线性减少,到21时为200人/小时.假定在不相重叠的时间间隔内到达车站的乘客数相互独立. 求(1)12时至14时恰有2000名乘客到车站的概率; (2)这两小时内到车站的乘客平均数. 解:以N (t )表示0时到t 时到达的乘客数,则 211818885),18(4001400,1400),5(400200)(≤≤<<≤≤?? ???---+=t t t t t t λ, (1)).21400(~)12()14(?-P N N ==-}2000)12()14({N N P ! 200028002000 2800?-e ; (5分) (2)2800)]12()14([=-N N E . (5分) 4.假定某天文台观测到的流星流是一个泊松过程,据以往资料统计为每小时平均观察到3颗流星. 试求 (1)在上午8点到12点期间,该天文台没有观察到流星的概率. (2)下午(12点以后)该天文台观察到第一颗流星的时间的分布函数. 解:(1)设早晨8时为0时刻,以N (t )表示0时到t 时观测到的流星数,则N (t )是强度为3(颗/小时)的泊松过程.).43(~)0()4(?-P N N ==-}0)0()4({N N P 12-e ; (5分)(完整版)北邮研究生概率论与随机过程2012-2013试题及答案
第十二章 平稳随机过程
第二章随机过程的基本概念
随机过程习题及答案
期末随机过程试题及标准答案
平稳随机过程
第1章 随机过程的基本概念
学期数理统计与随机过程(研)试题(答案)
随机过程试题及解答
平稳随机过程及其数字特征
随机过程作业题及参考答案(第一章)
随机过程答案-西交大
《概率论与随机过程》第1章习题答案
随机过程知识点汇总
随机过程2012A'卷及答案
第二章随机过程基本概念.
随机过程试题及答案
随机过程第三、五章测验题答案(2010)
