立体几何平行问题专题(学生版)

高三复习——立体几何平行问题专题(学生版)
——李洪波一、基础过关
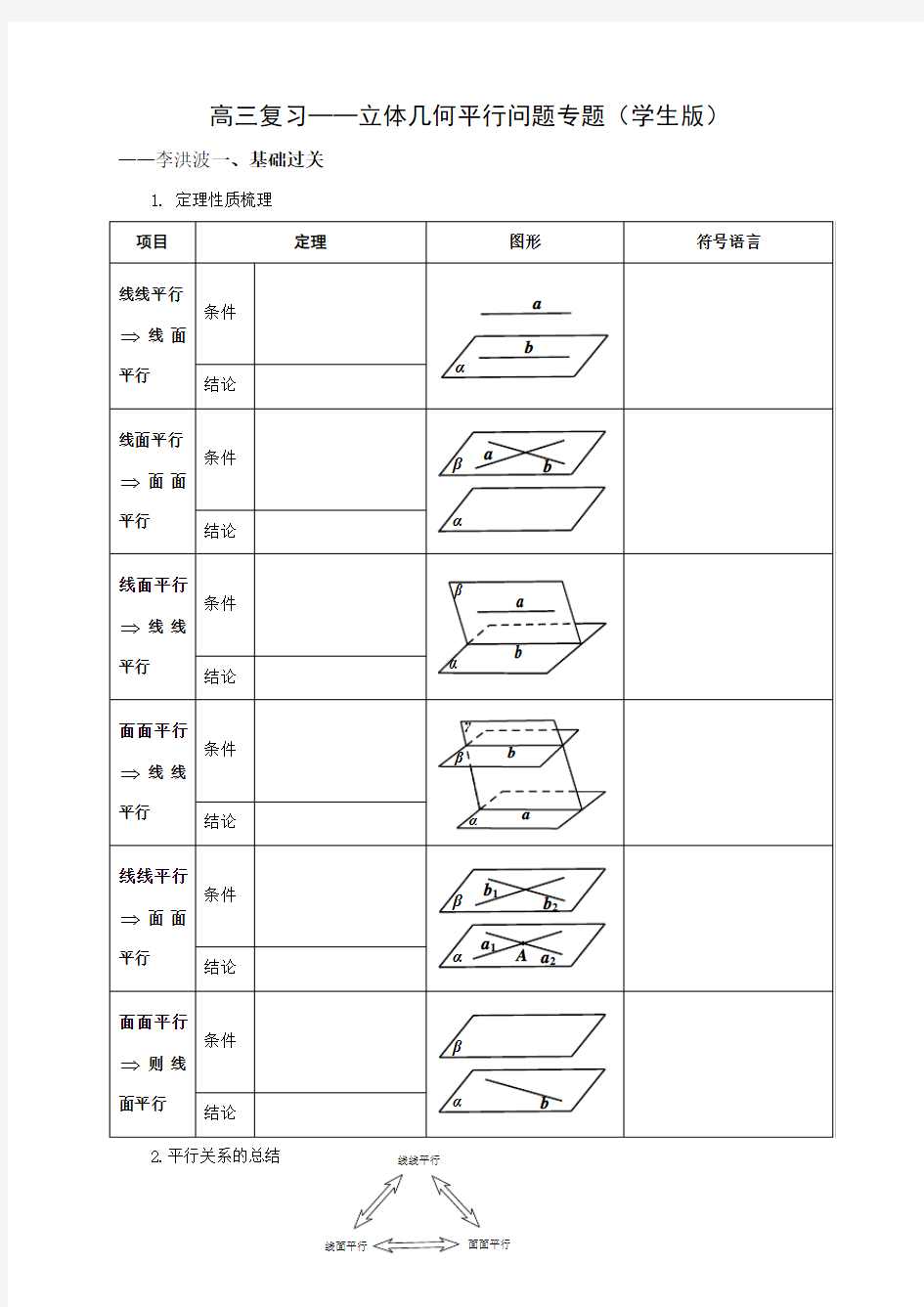
1. 定理性质梳理
2.平行关系的总结
面面平行
线面平行线线平行
二、概念理解——判断下列命题真假
(1)若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;( ) (2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;( ) (3)若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点;( ) (4)平行于同一平面的两条直线互相平行;( )
(5)αα//,//a b b a ??; ( ) (6)b a b a ////,//?αα; ( ) (7)αα////,//a b b a ?; ( ) (8)b a b a //,//??αα; ( ) (9)已知平面
α,β
和直线
m ,若,//,m m αβ?,则
α
练习:如图13,正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一 .求证:PQ∥平面BCE.
点P、Q,且AP DQ
解法二:(简要过程)
A
B
C
D
F
E
P
Q
解法三:(简要过程)
A
B
C
D
F
E
P
Q
四、举一反三
1.(17文科1)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是( )
2.(17文科2)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =
1
2
AD ,
∠BAD =∠ABC =90°.证明:直线BC∥平面PAD ;
3.(16文科3)如图,四棱锥中,平面,AD BC ,AB ,
4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.证明MN
平面PAB .
五、课堂小结:找线线平行的方法:(1)中位线;(2)平行四边形;(3)对应线段成比例
高中立体几何证明平行的专题
D B A 1 A F 立体几何——平行的证明 【例1】如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四边形 【例2】如图,已知直角梯形ABCD 中,AB∥CD,AB⊥BC,AB =1,BC =2,CD =1+3,过A 作AE⊥CD,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE⊥EC。 (Ⅰ)求证:BC⊥面CDE ; (Ⅱ)求证:FG∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 【例3】已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC⊥BE . 求证: (Ⅰ)C 1D⊥BC; (Ⅱ)C 1D∥平面B 1FM. 分 析 : 连 EA , 易 证 C 1EAD 是 平 行 四 是 (第1题图)
P E D C B A MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F G M AD CD BD BC AM EFG 求证: AB 1 ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC ∠=∠=//= 1 2 AD BE //= 12 AF ,G H ,FA FD BCHG ,,,C D F E ) 利用平行 四边形的性质 【例9】正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心,M 为BB 1的中点, 求证: D 1O 2 1 中点为PD E 求证:AE ∥平面PBC ; 分析:取PC 的中点F ,连EF 则易证ABFE 是平行四边形 【例11】在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB=90?,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF。若M是线段AD的中点,求证:GM∥平面ABFE; (I )证法一: 因为 EF 90ACB ∠=? 90,EGF ABC ∠=??. EFG ?BC FG 2 1= ABCD BC AM 2 1=FA ?GM ? A B C D E F G M
立体几何平行垂直问题专题复习
立体几何平行、垂直问题 【基础知识点】 一、平行问题 1.直线与平面平行的判定与性质 2.面面平行的判定与性质 平行问题的转化关系: 二、垂直问题 一、直线与平面垂直 1.直线和平面垂直的定义:直线l与平面a内的 ____________ 都垂直,就说直线丨与平面a互相垂直. 2.直线与平面垂直的判定定理及推论
该直线与此平面 垂直 推论 如果在两条平行直线中,有一条垂直于平面,那么另 一条直线也垂直这个平面 3.直线与平面垂直的性质定理 文字语言图形语言付号语言 性质定理垂直于同一个平面的两条直线平行 4.直线和平面垂直的常用性质 ①直线垂直于平面,则垂直于平面内任意直 线. ②垂直于同一个平面的两条直线平行. ③垂直于同一条直线的两平面平行. 二、平面与平面垂直 1.平面与平面垂直的判定定理 文字语言图形语言付号语言 判定定理一个平面过另一个平面的垂线,则这两个平面垂直 2.平面与平面垂直的性质定理 文字语言图形语言付号语言性质定理 两个平面垂直,则 一个平面内垂直于
交线的直线垂直于 另一个平面 【典例探究】 类型一、平行与垂直 例1、如图,已知三棱锥A BPC 中,AP PC, AC BC, M 为AB 中点,D 为PB 中点,且△ PMB 为正三角形。(I)求证: DM //平面 APC ; (U)求证:平面 ABC 平面APC ; (川)若BC 4,AB 20,求三棱锥 D BCM 的体积。 例2.如图,已知三棱柱 ABC A ,BQ 中,AA ,底面ABC , AC BC 2,AA , 4, AB 22,M 占 八、、? (I)求证:CN 平面ABB iA ; (U)求证:CN // 平面 AMB ,; (川)求三棱锥的体积. 【变式1】?如图,三棱柱ABC A 1B 1C 1中,侧棱AA i 平面ABC , ABC 为等 腰直角三角形, BAC 90,且 AB AA 1, D,E,F 分别是 B 1A,CC 1,BC 的中点。 (1)求证:DE//平面ABC ; 2)求证:B 1F 平面AEF ; (3)设AB a ,求三棱锥D AEF 的体积。 二、线面平行与垂直的性质 例3、如图4,在四棱锥P ABCD 中,平面PAD 平面ABCD , AB // DC , △ PAD 是等边三角形,已知BD 2AD 4, AB 2DC 2 5 . (1)求证:BD 平面PAD ; (2)求三棱锥A PCD 的体 B1 积. M N 分别是棱CC i ,AB 中 A i B A
2021高考数学立体几何专题
专题09立体几何与空间向量选择填空题历年考题细目表 题型年份考点试题位置 单选题2019 表面积与体积2019年新课标1理科12 单选题2018 几何体的结构特征2018年新课标1理科07 单选题2018 表面积与体积2018年新课标1理科12 单选题2017 三视图与直观图2017年新课标1理科07 单选题2016 三视图与直观图2016年新课标1理科06 单选题2016 空间向量在立体几何中的应 用2016年新课标1理科11 单选题2015 表面积与体积2015年新课标1理科06 单选题2015 三视图与直观图2015年新课标1理科11 单选题2014 三视图与直观图2014年新课标1理科12 单选题2013 表面积与体积2013年新课标1理科06 单选题2013 三视图与直观图2013年新课标1理科08 单选题2012 三视图与直观图2012年新课标1理科07 单选题2012 表面积与体积2012年新课标1理科11 单选题2011 三视图与直观图2011年新课标1理科06 单选题2010 表面积与体积2010年新课标1理科10 填空题2017 表面积与体积2017年新课标1理科16 填空题2011 表面积与体积2011年新课标1理科15 填空题2010 三视图与直观图2010年新课标1理科14 历年高考真题汇编 1.【2019年新课标1理科12】已知三棱锥P﹣ABC的四个顶点在球O的球面上,P A=PB=PC,△ABC是边长为2的正三角形,E,F分别是P A,AB的中点,∠CEF=90°,则球O的体积为() A.8πB.4πC.2πD.π 2.【2018年新课标1理科07】某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()
立体几何证明平行专题
A B C D B A 1 A F 立体几何证明平行专题训练 命题:*** 1. 如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分别为棱AB 、PD 的中点. 求证:AF ∥平面PCE ; 2、如图,已知直角梯形ABCD 中,AB∥CD,AB⊥BC,AB =1,BC =2,CD =1+3, 过A 作AE⊥CD,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE⊥EC. (Ⅰ)求证:FG∥面BCD ; (Ⅱ)求证:BC⊥面CDE ; 3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC⊥BE . 求证: (Ⅰ) C 1D∥平面B 1FM. (Ⅱ)C 1D⊥BC; (第1题图)
4、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 求证: //EB PAD 平面; 5、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 6、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE A B C D E F G M
P E D C B A 7.如图,三棱柱ABC —A 1B 1C 1中, D 为AC 的中点. 求 证 : AB 1ABEF ⊥ABCD ABEF ABCD 0 90,BAD FAB BC ∠=∠=//=12AD BE //=12AF ,G H ,FA FD //BC DHG 平面,,,C D F E 1C 2 1 中点为PD E 求证:AE ∥平面PBC ; 11、如图:S 是平行四边形ABCD 平面外一点,M 、N 分别是SA 、BD 上的点,且SM AM =ND BN , 求证:MN ∥平面SDC 12、如图,三棱锥ABC P -中,PB ⊥底面ABC ,90BCA ∠=,PB=BC=CA ,E 为PC 的中点,M 为AB 的中点,点F 在PA 上,且2AF FP =. (1)求证:BE ⊥平面PAC ; (2)求证://CM 平面BEF ;
高三文科数学立体几何平行垂直问题专题复习(含答案)
高三文科数学专题复习:立体几何平行、垂直问题 【基础知识点】 一、平行问题 1.直线与平面平行的判定与性质 定义判定定理性质性质定理 图形 条件a∥α 结论a∥αb∥αa∩α=a∥b 2. 面面平行的判定与性质 判定 性质 定义定理 图形 条件α∥β,a?β 结论α∥βα∥βa∥b a∥α 平行问题的转化关系: 二、垂直问题 一、直线与平面垂直 1.直线和平面垂直的定义:直线l与平面α内的都垂直,就说直线l与平面α互相垂直.2.直线与平面垂直的判定定理及推论 文字语言图形语言符号语言 判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平 面垂直 推论 如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直这个平面
文字语言 图形语言 符号语言 性质定理 垂直于同一个平面的 两条直线平行 4.直线和平面垂直的常用性质 ①直线垂直于平面,则垂直于平面内任意直线. ②垂直于同一个平面的两条直线平行. ③垂直于同一条直线的两平面平行. 二、平面与平面垂直 1.平面与平面垂直的判定定理 文字语言 图形语言 符号语言 判定定理 一个平面过另一个平 面的垂线,则这两个平 面垂直 2.平面与平面垂直的性质定理 文字语言 图形语言 符号语言 性质定理 两个平面垂直,则一个 平面内垂直于交线的直线垂直于另一个平 面 类型一、平行与垂直 例1、如图,已知三棱锥A BPC -中,,,AP PC AC BC ⊥⊥M 为AB 中点,D 为PB 中点, 且△PMB 为正三角形。(Ⅰ)求证:DM ∥平面APC ; (Ⅱ)求证:平面ABC ⊥平面APC ; (Ⅲ)若BC 4=,20AB =,求三棱锥D BCM -的体积。 M D A P B C
立体几何(小题)专题 历年高考真题模拟题汇总(解析版)
立体几何 一、年考试大纲 二、新课标全国卷命题分析 三、典型高考试题讲评 2011—年新课标全国(1卷、2卷、3卷)理科数学分类汇编——11.立体几何 一、考试大纲 1.空间几何体 (1)认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构. (2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图. (3)会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式. (4)会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求). (5)了解球、棱柱、棱锥、台的表面积和体积的计算公式. 2.点、直线、平面之间的位置关系 (1)理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理. 公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内. 公理2:过不在同一条直线上的三点,有且只有一个平面. 公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 公理4:平行于同一条直线的两条直线互相平行. 定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. (2)以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理. 理解以下判定定理. 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行. 如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行. 如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直. 如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直. 理解以下性质定理,并能够证明. 如果一条直线与一个平面平行,那么经过该直线的任一个平面与此平面的交线和该直线平行. 如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行. 垂直于同一个平面的两条直线平行. 如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直. 3.能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题. 4.空间直角坐标系 (1)了解空间直角坐标系,会用空间直角坐标表示点的位置. (2)会推导空间两点间的距离公式. 二、新课标全国卷命题分析 立体几何小题常考的题型包括:(1)球体;(2)多面体的三视图、体积、表面积或角度,包括线线角、
高考中常见的立体几何题型和解题方法
高考中常见的立体几何题型和解题方法 黔江中学高三数学教师:付 超 高考立体几何试题一般共有2——3道(选择、填空题1——2道, 解答题1道), 共计总分18——23分左右,考查的知识点在20个以内. 选择填空题考核立几中的 逻辑推理型问题, 而解答题着重考查立几中的计算型问题, 当然, 二者均应以正 确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多 一点思考,少一点计算”的方向发展.从历年的考题变化看, 以简单几何体为载体 的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合 1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过 程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与 距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行 与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能, 通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平 行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能 力和空间想象能力. 2. 判定两个平面平行的方法: (1)根据定义——证明两平面没有公共点; (2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面; (3)证明两平面同垂直于一条直线。 3.两个平面平行的主要性质: ⑴由定义知:“两平行平面没有公共点”。 ⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平 面。 ⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交, 那 么它们的交线平行”。 ⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。 ⑸夹在两个平行平面间的平行线段相等。 ⑹经过平面外一点只有一个平面和已知平面平行。 以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过 程中均可直接作为性质定理引用。 4.空间角和距离是空间图形中最基本的数量关系,空间角主要研究射影以 及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角 和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解 决. 空间角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系 进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线 所成的角θ∈(0,2π],直线与平面所成的角θ∈0,2π?????? ,二面角的大小,可用它们的平面角来度量,其平面角θ∈[0,π].对于空间角的计算,总是通过一定 的手段将其转化为一个平面内的角,并把 它置于一个平面图形,而且是一个三
立体几何平行垂直问题专题复习
立体几何平行、垂直问题【基础知识点】 一、平行问题 1.直线与平面平行的判定与性质 定义判定定理性质性质定理图形 条件a∥α 结论a∥αb∥αa∩α=a∥b 2. 面面平行的判定与性质 判定 性质 定义定理 图形 条件α∥β,a?β 结论α∥βα∥βa∥b a∥α 平行问题的转化关系: 二、垂直问题
一、直线与平面垂直 1.直线和平面垂直的定义:直线l与平面α内的都垂直,就说直线l 与平面α互相垂直. 2.直线与平面垂直的判定定理及推论 文字语言图形语言符号语言 判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直 推论 如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直这个平面 3.直线与平面垂直的性质定理 文字语言图形语言符号语言性质定理 垂直于同一个平面 的两条直线平行 ①直线垂直于平面,则垂直于平面内任意直
线. ②垂直于同一个平面的两条直线平行. ③垂直于同一条直线的两平面平行. 二、平面与平面垂直 【典例探究】 类型一、平行与垂直 例1、如图,已知三棱锥A BPC -中, ,,AP PC AC BC ⊥⊥M 为AB
F D E C1 A1 C A 中点,D 为PB 中点,且△PMB 为正三角形。(Ⅰ)求证:DM ∥平面APC ; (Ⅱ)求证:平面ABC ⊥平面APC ; (Ⅲ)若BC 4=,20AB =,求三棱锥D BCM -的体积。 例 2. 如图,已知三棱柱111ABC A B C -中,1AA ⊥底面ABC ,2AC BC ==,14AA =, 22AB =,M ,N 分别是棱1CC ,AB 中点. (Ⅰ)求证:CN ⊥平面11ABB A ; (Ⅱ)求证://CN 平面1AMB ; (Ⅲ)求三棱锥1B AMN -的体积. 【变式1】. 如图,三棱柱111C B A ABC -中,侧棱1AA ⊥平面ABC ,ABC ?为等腰直角 三角形, 90=∠BAC ,且1AA AB =,F E D ,,分别是BC CC A B ,,11的中点。 (1)求证://DE 平面ABC ; (2)求证:⊥F B 1平面AEF ; (3)设AB a =,求三棱锥D AEF -的体积。 二、线面平行与垂直的性质 例3、如图4,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,AB DC ∥,PAD △是等边三角形,已知24BD AD ==,225AB DC == A B C A 1 B 1 C 1 M N
高三立体几何专题复习
高三立体几何专题复习 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
高考立体几何专题复习 一.考试要求: (1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图,能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。 (2)了解空两条直线的位置关系,掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念(对于异面直线的距离,只要求会计算已给出公垂线时的距离)。 (3)了解空间直线和平面的位置关系,掌握直线和平面平行的判定定理和性质定理,理解直线和平面垂直的判定定理和性质定理,掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念,了解三垂线定理及其逆定理。 (4)了解平面与平面的位置关系,掌握两个平面平行的判定定理和性质定理。掌握二面角、二面角的平面角、两个平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理。 (5)会用反证法证明简单的问题。 (6)了解多面体的概念,了解凸多面体的概念。 (7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。 (8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。 (9)了解正多面体的概念,了解多面体的欧拉公式。 (10)了解球的概念,掌握球的性质,掌握球的表面积、体积公式。 二.复习目标: 1.在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上,研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用;在有关问题的解决过程中,进一步了解和掌握相关公理、定理的内容和功能,并探索立体几何中论证问题的规律;在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用. 2.在掌握空间角(两条异面直线所成的角,平面的斜线与平面所成的角及二面角)概念的基础上,掌握它们的求法(其基本方法是分别作出这些角,并将它们置于某个三角形内通过计算求出它们的大小);在解决有关空间角的问题的过程中,进一步巩固关于直线和平面的平行垂直的性质与判定的应用,掌握作平行线(面)和垂直线(面)的技能;通过有关空间角的问题的解决,进一步提高学生的空间想象能力、逻辑推理能力及运算能力. 3.通过复习,使学生更好地掌握多面体与旋转体的有关概念、性质,并能够灵活运用到解题过程中.通过教学使学生掌握基本的立体几何解题方法和常用解题技巧,发掘不同问题之间的内在联系,提高解题能力. 4.在学生解答问题的过程中,注意培养他们的语言表述能力和“说话要有根据”的逻辑思维的习惯、提高思维品质.使学生掌握化归思想,特别是将立体几何问题转化为平面几何问题的思想意识和方法,并提高空间想象能力、推理能力和计算能力. 5.使学生更好地理解多面体与旋转体的体积及其计算方法,能够熟练地使用分割与补形求体积,提高空间想象能力、推理能力和计算能力. 三.教学过程: (Ⅰ)基础知识详析 重庆高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立
立体几何平行问题专题(学生版)
高三复习——立体几何平行问题专题(学生版) ——李洪波一、基础过关 1. 定理性质梳理 2.平行关系的总结 面面平行 线面平行线线平行
二、概念理解——判断下列命题真假 (1)若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;( ) (2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;( ) (3)若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点;( ) (4)平行于同一平面的两条直线互相平行;( ) (5)αα//,//a b b a ??; ( ) (6)b a b a ////,//?αα; ( ) (7)αα////,//a b b a ?; ( ) (8)b a b a //,//??αα; ( ) (9)已知平面 α,β 和直线 m ,若,//,m m αβ?,则 α
练习:如图13,正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一 .求证:PQ∥平面BCE. 点P、Q,且AP DQ
解法二:(简要过程) A B C D F E P Q 解法三:(简要过程) A B C D F E P Q 四、举一反三 1.(17文科1)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是( ) 2.(17文科2)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC = 1 2 AD ,
∠BAD =∠ABC =90°.证明:直线BC∥平面PAD ; 3.(16文科3)如图,四棱锥中,平面,AD BC ,AB , 4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.证明MN 平面PAB .
2010年高考立体几何专题复习-6
2010年高考立体几何专题复习 岱山中学 孙珊瑚 鲁纪伟 高考立体几何试题一般有选择、填空题, 解答题,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合 1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力. 2.判定两个平面平行的方法: (1)根据定义——证明两平面没有公共点; (2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面; (3)证明两平面同垂直于一条直线。 3.两个平面平行的主要性质: ⑴由定义知:“两平行平面没有公共点”。 ⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。 ⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那 么它们的交线平行”。 ⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。 ⑸夹在两个平行平面间的平行线段相等。 ⑹经过平面外一点只有一个平面和已知平面平行。 以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过程中均可直接作为性质定理引用。 4.空间的角和距离是空间图形中最基本的数量关系,空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决. 空间的角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概 念,由它们的定义,可得其取值范围,如两异面直线所成的角θ∈(0,2π],直线与平面所成的角θ∈0,2π?? ???? , 二面角的大小,可用它们的平面角来度量,其平面角θ∈[0,π]. 对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力. 如求异面直线所成的角常用平移法(转化为相交直线)与向量法;求直线与平面所成的角常利用射影转化为相交直线所成的角;而求二面角-l -的平面角(记作)通常有以下几种方法: (1) 根据定义; (2) 过棱l 上任一点O 作棱l 的垂面,设∩=OA ,∩=OB ,则∠AOB = ; (3) 利用三垂线定理或逆定理,过一个半平面内一点A ,分别作另一个平面的垂线AB (垂足为B ),或棱l 的垂线AC (垂足为C ),连结AC ,则∠ACB = 或∠ACB =-; (4) 设A 为平面外任一点,AB ⊥,垂足为B ,AC ⊥,垂足为C ,则∠BAC =或∠BAC =-; (5) 利用面积射影定理,设平面内的平面图形F 的面积为S ,F 在平面内的射影图形的面积为S ,则cos =S S ' . 5.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线
高中立体几何证明平行的专题训练1
高中立体几何证明平行的专题训练 立体几何中证明线面平行或面面平行都可转化为线线平行,而证明线线平行一般有以下的一些方法: (1)通过“平移”。(2)利用三角形中位线的性质。(3)利用平行四边形的性质 (3)利用对应线段成比例。(4)利用面面平行,等等。 第一类 通过“平移”再利用平行四边形的性质 1. 如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点. 求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG .,FG ,则易证AEGF 是平行四边形 2、如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1, BC =2,CD =1+ 3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC. (Ⅰ)求证:BC ⊥面CDE ; (Ⅱ)求证:FG ∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, (第1题图)
D E B 1 A 1 C 1 C A B F M M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EA 4、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证 明: //EB PAD 平面; 分析::取PD 的中点F ,连EF,AF 则易证ABEF 是平行四边形 第二类 利用三角形中位线的性质 5、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥ 平面EFG 。 分析:连MD 交GF 于H ,易证EH 是△AMD 的中位线 6、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 A B C D E F G M
高中立体几何证明线面平行的常见方法
D E B 1 A 1 C 1 C A B M 高中立体几何证明线面平行问题(数学作业十七) (1) 通过“平移”再利用平行四边形的性质 1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分别为棱AB 、 PD 的中点.求证: AF ∥平面PCE ; 2、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 3、如图所示, 四棱锥P ABCD 底面是直角梯形, E F B A C D P (第
,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; (2) 利用三角形中位线的性质 4、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 5、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE 6.如图,三棱柱ABC —A 1B 1C 1中, D 为AC A B C D E F G M
P E D C B A 的中点. 求证:AB 12 1中点为PD E 求证:AE ∥平面PBC ; (4)利用对应线段成比例 9、如图:S 是平行四边形ABCD 平面外一点,M 、N 分别是SA 、 BD 上的点,且SM AM =ND BN , 求证:MN ∥平面SDC (5)利用面面平行 10、如图,三棱锥ABC P -中,PB ⊥底面,90BCA ∠=o ,PB=BC=CA , 为的中点,为的中点,点在上,且2AF FP =. (1)求证:BE ⊥平面; (2)求证://CM 平面;
(完整版)立体几何中平行与垂直证明方法归纳
c c ∥∥b a b a ∥?本文档系统总结归纳了立体几何中平行与垂直证明方法,特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。是一份不可多得的好资料。 一、“平行关系”常见证明方法 (一)直线与直线平行的证明 1) 利用某些平面图形的特性:如平行四边形的对边互相平行 2) 利用三角形中位线性质 3) 利用空间平行线的传递性(即公理4): 平行于同一条直线的两条直线互相平行。 4) 利用直线与平面平行的性质定理: 如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。 5) 利用平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 6) 利用直线与平面垂直的性质定理: 垂直于同一个平面的两条直线互相平行。 a b α β b a a =??βαβ α∥b a ∥? b a b a ////??? ? ?? ==γβγαβαI I β α ⊥⊥b a b a ∥?α a b
7) 利用平面内直线与直线垂直的性质: 在同一个平面内,垂直于同一条直线的两条直线互相平行。 8) 利用定义:在同一个平面内且两条直线没有公共点 (二)直线与平面平行的证明 1) 利用直线与平面平行的判定定理: 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。 2) 利用平面与平面平行的性质推论: 两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。 3) 利用定义:直线在平面外,且直线与平面没有公共点 (三)平面与平面平行的证明 常见证明方法: 1) 利用平面与平面平行的判定定理: 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。 α b a β α a β αα∥?a β ∥a ?α αββ////∩??b a P b a b a =α β//?α β b a P b ∥a b a αα??α ∥a ?
立体几何证明平行的方法及专题训练
D B A 1 立体几何证明平行的方法及专题训练 罗虎胜https://www.360docs.net/doc/2f4664373.html, 立体几何中证明线面平行或面面平行都可转化为 线线平行,而证明线线平行一般有以下的一些方法: (1) 通过“平移”。 (2) 利用三角形中位线的性质。 (3) 利用平行四边形的性质。 (4) 利用对应线段成比例。 (5) 利用面面平行的性质,等等。 (1) 通过“平移”再利用平行四边形的性质 1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四边形 2、如图,已知直角梯形ABCD 中,AB∥CD,AB⊥BC,AB =1,BC =2,CD =1+3, 过A 作AE⊥CD,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE⊥EC. (Ⅰ)求证:BC⊥面CDE ; (Ⅱ)求证:FG∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB (第1题图)
M 为BE 的中点, AC⊥BE . 求证: (Ⅰ)C 1D⊥BC; (Ⅱ)C 1D∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EA 4、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; 分析::取PD 的中点F ,连EF,AF 则易证ABEF 是 平行四边形 (2) 利用三角形中位线的性质 5、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证: AM ∥平面EFG 。 分析:法一:连MD 交GF 于H ,易证EH 是△AMD 的中位线 法二:证平面EGF ∥平面ABC ,从而AM ∥平面EFG 6、如图,直三棱柱///ABC A B C -,90BAC ∠=, 2,AB AC ==AA ′=1,点M ,N 分别为/A B 和//B C 的中点。 A B C D E F G M
高中立体几何证明平行的专题训练
高中立体几何证明平行的专题训练 深圳市龙岗区东升学校一一罗虎胜 立体几何中证明线面平行或面面平行都可转化为 线线平行,而证明线线平行一般有以下的一些方法: (1)通过“平移”。 (2)利用三角形中位线的性质。 (3)利用平行四边形的性质。 (4)利用对应线段成比例。 (5)利用面面平行,等等。 ⑴通过“平移”再利用平行四边形的性质 1. 如图,四棱锥P—ABCD的底面是平行四边形,点E、F 分另为棱AB、PD的中点.求证:AF //平面PCE; P 分析:取PC的中点G,连EG.,FG,则易证AEGF是平行四边形 F E A (第1题 图) 2、如图,已知直角梯形ABCD 中,AB // CD,AB 丄BC,AB = 1,BC = 2,CD = 1 + -?. 3,过A作AE丄CD,垂足为E,G、F分别为AD、CE的中点,现将△ ADE沿AE折叠,使得DE 丄EC. (I)求证:BC 丄面CDE ; (H)求证:FG //面BCD ; 分析:取DB的中点H,连GH,HC贝惕证FGHC是平行四边形
的中点,证明:EB//平面PAD ; 分析::取PD 的中点F ,连EF,AF 则易证 ABEF 是 平行四边形 (2)利用三角形中位线的性质 5、如图,已知E 、F 、G 、M 分别是四面体的棱 AD AM //平面 EFG 。 3、已知直三棱柱 ABC — A 1B 1C 1中,D, E, F 分别为 AA 1, CC 1, AB 的中点, M 为BE 的中点,AC 丄BE.求证: (i) C 1D 丄BC ; (n) C 1D //平面 B i FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是 MF//EA D A A 1 4、如图所示,四棱锥P ABCD 底面是直角梯形, BA AD, CD AD ,CD=2AB, E 为 PC 分析:连 MD 交GF 于H ,易证EH 是厶AMD 的中位线 6、如图,ABCD 是正方形,0是正方形的中心, E 是PC C
高中数学-立体几何位置关系-平行与垂直证明方法汇总
高中数学-立体几何位置关系-平行与垂直证明方法汇总 (一)立体几何中平行问题 证明直线和平面平行的方法有: ①利用定义采用反证法; ②平行判定定理; ③利用面面平行,证线面平行。 主要方法是②、③两法 在使用判定定理时关键是确定出面内的 与面外直线平行的直线. 常用具体方法:中位线和相似 例1、P是平行四边形ABCD所在平面外一点,Q是PA的中点. 求证:PC∥面BDQ. 证明:如图,连结AC交BD于点O. ∵ABCD是平行四边形, ∴A O=O C.连结O Q,则O Q在平面BDQ内, 且O Q是△APC的中位线, ∴PC∥O Q. ∵PC在平面BDQ外, ∴PC∥平面BDQ. 例2、在棱长为a的正方体ABCD-A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.求证: (1)E、F、B、D四点共面; (2)面AMN∥面EFBD.
证明:(1)分别连结B 1D 1、ED 、FB ,如图, 则由正方体性质得 B 1D 1∥BD. ∵E 、F 分别是D 1C 1和B 1C 1的中点, ∴EF ∥ 21B 1D 1.∴EF ∥2 1 BD. ∴E 、F 、B 、D 对共面. (2)连结A 1C 1交MN 于P 点,交EF 于点Q ,连结AC 交BD 于点O ,分别连结PA 、Q O . ∵M 、N 为A 1B 1、A 1D 1的中点, ∴MN ∥EF ,EF ?面EFBD. ∴MN ∥面EFBD. ∵PQ ∥A O , ∴四边形PA O Q 为平行四边形. ∴PA ∥O Q. 而O Q ?平面EFBD , ∴PA ∥面EFBD.且PA ∩MN=P ,PA 、MN ?面AMN , ∴平面AMN ∥平面EFBD. 例3如图(1),在直角梯形P 1DCB 中,P 1D//BC ,CD ⊥P 1D ,且P 1D=8,BC=4,DC=4 6, A 是P 1D 的中点,沿A B 把平面P 1AB 折起到平面PAB 的位置(如图(2)),使二面角P —CD —B 成45°,设E 、F 分别是线段AB 、PD 的中点. 求证:AF//平面PE C ; 证明:如图,设PC 中点为G ,连结FG ,
立体几何中的平行问题
1 思维拓展: 如图,ABCD 是平行四边形,M,N 分别是AB,PC 的中点. 求证MN//面PAD (你能思考出几种方法?) 【例3】如图,已知正方体 中,面对角线,上分别有两点E 、F ,且.求证:EF ∥平面ABCD . 例2、已知 正方体ABCD-A 1B 1C 1D 1求证:平面AB 1D 1//平面BC 1D 【例2】如图,设平面∥平面,AB 、CD 是两异面直线,M 、N 分别是AB 、CD 的中点,且A 、C∈,B 、D∈. 求证:. 1111 A B C D A B C D -1A B 1 B C 11B E C F =αβαβ//M N αA B C D F E C 1 B 1A 1 D 1 D 1 B 1 A 1 D C B A C 1α β A B C D M N P C
2 变式1、如图,直线相交于点O ,,, 求证:平面ABC //平面 6、设是单位正方体的面、面的中心,如图 8-4,证明:⑴∥平面;⑵面 ∥面. 变式2、如图:空间四边形ABCD 中,E 、F 、 G 、H 分别为AB 、BC 、CD 、DA 上的点,若AC//平面EFGH ,BD//平面EFGH, 求证: EFGH 为平行四 边形 3.判断正误 (1)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( ) (2)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( ) (3)设l 为直线,α,β是两个不同的平面,若l∥α,l∥β,则α∥β.( ) ' '' ,,CC BB AA ,'O A AO =O B BO ' =O C CO ' =' ' ' C B A ,P Q 1A C 11A A D D 1111A B C D P Q 11A A B B 1D P Q 1C D B
重点高中立体几何证明平行的专题
重点高中立体几何证明平行的专题
————————————————————————————————作者:————————————————————————————————日期: 2
3 F G G A B C D E C A B D E F D E B 1 A 1 C 1C A B F M 立体几何——平行的证明 【例1】如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG .,FG ,则易证AEGF 是平行四边形 【例2】如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1,BC =2,CD =1 +3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC 。 (Ⅰ)求证:BC ⊥面CDE ; (Ⅱ)求证:FG ∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 【例3】已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EA E F B A C D P (第1
4 【例4】如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; 分析::取PD 的中点F ,连EF,AF 则易证ABEF 是平行四边形 (2) 利用三角形中位线的性质 【例5】如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 分析:连MD 交GF 于H ,易证EH 是△AMD 的中位线 【例6】如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE 【例7】如图,三棱柱ABC —A 1B 1C 1中, D 为AC 的中点. 求证:AB 1//面BDC 1; 分析:连B 1C 交BC 1于点E ,易证ED 是 △B 1AC 的中位线 A B C D E F G M
