博弈论第四章

4 非完全信息动态博弈

4.1 精炼贝叶斯均衡概述

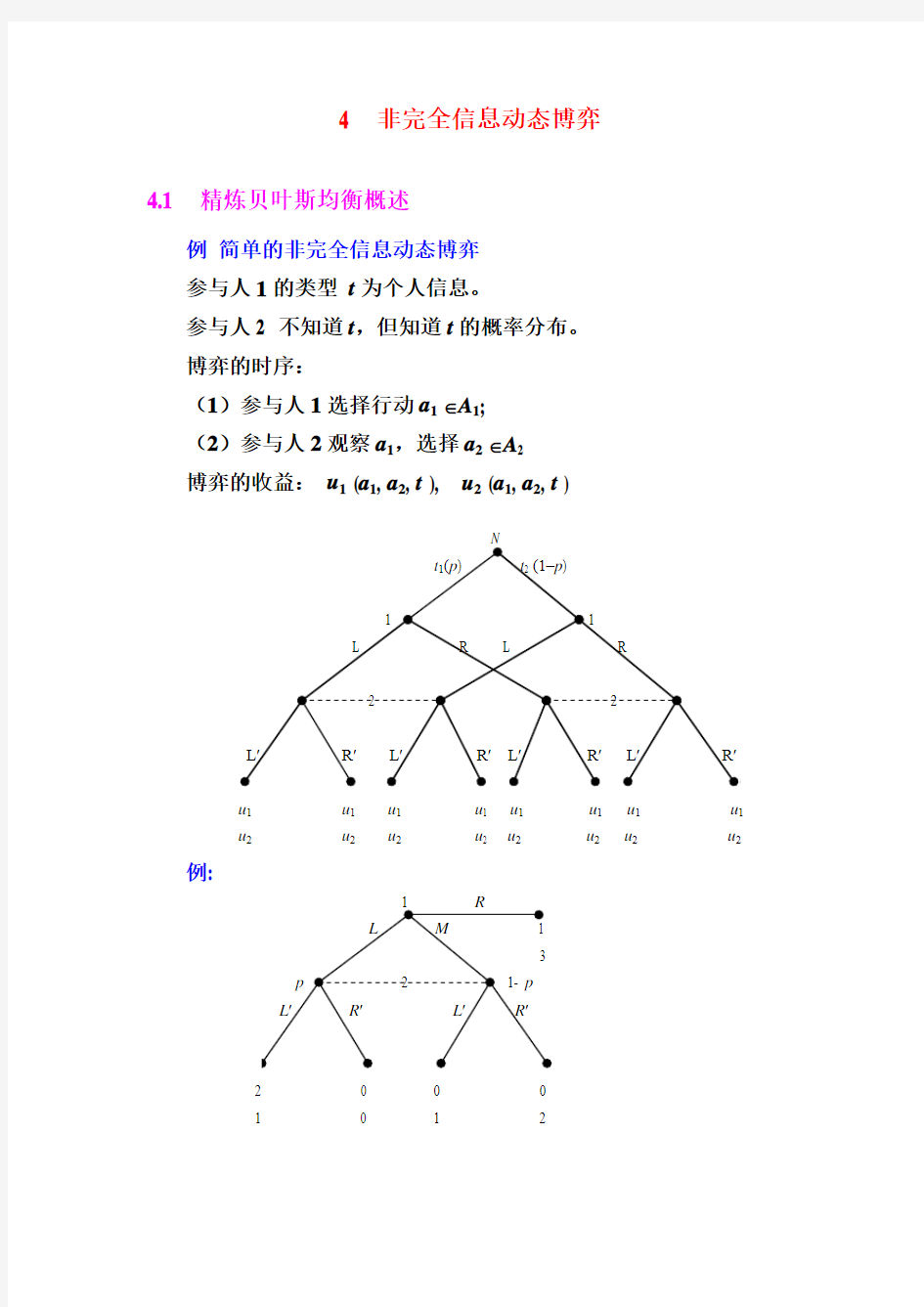
例简单的非完全信息动态博弈

参与人1的类型t为个人信息。

参与人2 不知道t，但知道t的概率分布。

博弈的时序：

（1）参与人1选择行动a1∈A1;

（2）参与人2观察a1，选择a2∈A2

博弈的收益：u1 (a1, a2, t ), u2 (a1, a2, t )

u1u1u1u1 u1u1u1u1

u2u2u2u2 u2u2u2u2例:

1 R

L M 1

3

p 2 1- p

L'R'L'R'

2 0 0 0

1 0 1 2

标准式表示

参与人2

L'R'

L2，10，0

参与人1 M0, 20， 1

R1, 31, 3

纯战略纳什均衡: (L，L'), (R，R')

均为子博弈精炼纳什均衡(无子博弈)。

但是(R, R')不可信。

排除不可信的纳什均衡：

要求1 参与人必须有一个推断(belief).

要求2 参与者的战略必须满足序贯理性(sequentially rational).

定义

处于均衡路径上(on the equilibrium path)的信息集: 在均衡战略下，博弈以正的概率到达该集.

处于均衡路径之外(off the equilibrium path)的信息集: 在均衡战略下，博弈不会到达此集.

要求 3 在处于均衡路径上的信息集上, 推断由贝叶斯法则和参与人的均衡战略决定。

例要求3的说明

参与人1的类型空间：{ t1，t2，t3，t4 }

行动空间：A= { L，R}

推断p i : 观察到L 后，参与人1的类型是t i 的概率。 推断q i : 观察到R 后，参与人1的类型是t i 的概率。 p 1 + p 2 + p 3 + p 4 = 1 q 1 + q 2 + q 3 + q 4= 1

如果参与人1的战略： t 1选 L ，t 2选 L ， t 3选R ，t 4 选R 。 参与人2对p i 与 q i 的推断： p 1 =

3.02.02.0+= 0.4, p 2 = 3

.02.03

.0+= 0.6, p 3 = 0, p 4 =0;

q 1 = 0, q 2= 0, q 3 =3.02.02.0+= 0.4, q 4= 3

.02.03

.0+= 0.6,

要求 4 在处于均衡路径之外的信息集上, 可能情况下，推断由贝叶斯法则和参与人的均衡战略决定。

原文：At information sets off the equilibrium path, beliefs are determined by Bayes ’ rule and the players ’ equilibrium strategies

where possible.

精炼贝叶斯均衡(perfect Bayesian equilibrium)：在一个非完全信息的动态博弈中，满足要求1 – 4 的战略与推断构成的均衡。

例不满足要求4的情形。

3个参与人的博弈。

1 A 2

D 0

2

L R

[p] [1 –p]

3

L'R'L'R'

1 3 0 0

2 3 1 1

1 3

2 1

子博弈精炼纳什均衡: (D, L, R')

另有战略(A, L, L')和推断p = 0:

----纳什均衡

----满足要求1-3.

----不是精炼贝叶斯均衡: 不满足要求4: p= 0 与2的战略不相容.

例要求4中“不可能”的情形。

1 A

D

2 A'

L R1-q1-q2

[q1] [q2]

3

L'R'L'R'

如果(A, A', L') 是均衡，则参与人3的战略要针对参与人2的L 或R。

参与人3的推断必须是p = q1/(q1 + q2)

但是参与人2选A'，q1 + q2 =0, 因此无法计算p。

4.2 信号博弈

4.2.A 信号博弈中的精炼贝叶斯均衡

信号博弈的参与人：信号发送者S，接收者R。

信号博弈的时间顺序

自然按照概率分布为S产生一个t i∈T

S观察t，并选择m j∈M

R观察m并选择a k∈A

收益U S(t i，m j，a k)和U R(t i，m j，a k)

信号博弈的例

T = {t1, t2}, M = {m1, m2}, A = {a1, a2},

Pr{t 1} = p , Pr{t 2} = 1 - p 。

发送者战略: 在类型为t 1时发出的信号与t 2时发出的信号：

{m 1, m 1}, {m 1, m 2}, {m 2, m 1}, {m 2, m 2} 混同(pooling)战略: 所有的类型发出相同的信号：

{m 1, m 1}, {m 2, m 2}

分离(separating)战略：不同的类型发出不同的信号：

{m 1, m 2}, {m 2, m 1}

接收者战略: 在收到信号m 1时与信号m 2时选择的行动： { a 1, a 1}, {a 1, a 2}, {a 2, a 1}, {a 2, a 2}

1，

3，1

2，2，0 3，1，0

1，2，2

信号要求 1: 接收者在观察信号m j 后，必须对发送m j 的类型有一个推断

∑∈T

t i μ( t i ∣m j ) = 1

信号要求 2R : 对每一 m j , 接收者的行动 a *(m j ) 必须在给定推断 μ( t i | m j ) 后，最大化他的期望效用,

A

a k ∈max

∑∈T

t i μ( t i | m j ) U R (t i , m j , a k )

信号要求 2S : 对每一t i , 在给定a *(m j ) 后，发送者的信号 m *(t i )必须最大化他的效用

M

m j ∈max U S (t i , m j , a *(m j ))

信号要求 3: 对每一 m j , 如果存在 t i 使得 m *(t i ) = m j , 则接收者的推断:

μ( t i | m j ) =

∑)

()

(i i t p t p 精炼贝叶斯均衡: 战略 (m *(t i ), a *(m j ))和推断 μ(t i | m j ) 满足信号要求 (1), (2R), (2S),和 (3)。

为什么没有要求4？

例 T = {t 1, t 2, t 3, t 4}, M = {m 1, m 2, m 3} 如果在均衡中，发送者的战略：

m *(t 1) = m 1，m *(t 2) = m 1，m *(t 3) = m 2，m *(t 4) = m 2 则m 3处于均衡路径以外，若用贝叶斯公式，分母为0。

例 (Figure 4.2.2)

1， 2，1

4， 0，0 2， 1，0

0， 1，2

求精炼贝叶斯均衡：对4种情况逐一分析。 1. 混同于L ?

发送者: (L, L).

如果为均衡，p = 0.5

接收者收益分别为: 3.5(u)，或0.5(d)。将选择u。

发送者收益分别为：1 (t1)，2 (t2)

如果发送者发送R, 当

q + (1 –q)×0 ≤q×0 + (1 –q)×2

q≤ 2/3

接收者将选择d. 发送者收益为0(t1),和1(t2), 小于发送L时分别所得。

均衡: { (L, L), (u, d), p = 0.5, q≤ 2/3}

2. 混同于R?

发送者: (R, R)

如果是均衡，q = 0.5.

接收者的收益: 0.5 (u), 1 (d)。他选择d

发送者的收益分别为: 0 (t1), 1 (t2)

如果发送者在t1时发送L, 收益至少为1。

不是均衡。

3. 分离(L, R)?

发送者: (L, R).

接收者推断：p = 1 , q = 0

接收者战略: (u, d)。

发送者的收益分别为：1 (t1), 1 (t2)

但是对t2, 如果发送者发送L, 接收者选择u, 发送者的收益将为2。发送者在t2时，将发送L。

不是均衡。

4. 分离(R, L)?

发送者: (R, L)。

接收者推断：p = 0, q = 1，战略：(u, u)

发送者的收益分别为：2(t1), 2 (t2)

如果发送者不这样, 收益将为1(t1发送L)，和1(t2发送R)。

分离精炼贝叶斯均衡:

[(R, L), (u, u), p = 0, q = 1]

4.2.B就业市场的信号博弈。

1．自然决定工人的能力η，以概率q为高H，以概率1 –q为低L。

2．工人了解自己的能力，选择一个教育水平e≥ 0，教育的成本为c(H，e)或c( L，e)。

假设对于获得相同的教育，低能力工人的边际成本要高于高能力的工人的，即c e(L, e ) > c e ( H, e)

c e c e(L, e )

c e ( H, e)

e

3．企业观察e，决定工人的工资w。

工人的收益w–c( η，e)

工人的无差异曲线I(e, w) = w–c( η，e)

斜率 k = -//dI de

dI dw

= c e

w I L

I H

e

企业的收益 y ( η，e ) – w

假设企业是完全竞争的，即w = y ( η，e )

w

y (H , e )

w H *

y (L , e )

w L *

e L * e s e H *

具有能力η 的工人选择教育水平e 使得

e

max w – c (η, e )

s . t . y (η, e ) = w

最优解表示为e *(η)，对应的工资w *(η) = y [η, e *(η)]

低能力工人不冒充高能力工人的情形，即

w *(L ) – c [L , e *(L )] > w *(H ) – c [L , e *(H )]

w

w H*

w L*

e L* e s e H*

在有冒充的情形，即

w*(H) –c[L, e*(H)] > w*(L) –c[L, e*(L)]

w

y(H, e s )

w H*

w L*

e L* e H* e s e' e

1．混同均衡

只有存在冒充时，才可能有混同均衡。

两种工人选择同一种教育水平e p，公司观察到e p后的判断为p(H|e p) = q

支付的工资为

w p = qy (H, e p) + (1 –q) y(L, e p) （4.2.2）对于不在均衡路径上的判断，可以是

p(H|e) = 0 e≠e p

工资支付为

w(e) = y(L，e) e≠e p

w

y(H, e s )

w L*

e L* e p e'e''e s e

其他的混同均衡：e0: e p < e0 < e'，类似给出公司的判断及工资的支付，也构成完备贝叶斯均衡。

另一种混同均衡：e p，但公司对不在均衡路径上的判断不同。

0 e≤e"e≠e p

μ(H| e) = q e = e p

q e > e"

公司的工资支付为

y(L, e) e≤e"e≠e p

w(e) = w(e p ) e = e p

w(e) e > e"

2．分离均衡

（1）不存在冒充的时候

e(L) = e L*，e(H) = e H*，

公司的判断：

p(H| e) = 0，e < e H*

p(H| e) = 1，e≥e H*

公司支付工资

w (e) = y(L，e H*)，e < e H*

w (e) = y(H，e L*)，e≥e H*

这是完备贝叶斯均衡。

（2）存在冒充的时候

高能力工人选择e s > e*(H)，低能力选择e = e*(L)

公司的判断及公司支付工资为：

μ (H| e) = 0，e < e s

μ (H| e) = 1，e≥e s

w (e) = y(L，e H*)，e < e s

w (e) = y(H，e L*)，e≥e s

可以构成分离均衡。

w

y(H, e s )

w H*

w L*

e L* e H* e s e' e

考虑e' > e s。

分离均衡: 高能力工人选择e'，低能力工人选择e L*。

公司的判断及工资支付为

μ(H| e) = 0，e < e'

μ(H| e) = 1，e≥e'

w (e) = y(L，e L*)，e < e'

w (e) = y(H，e)，e≥e'

这是完备贝叶斯均衡。

混杂均衡。

一种工人以确定性选择一个教育水平，另一种随机选择前一种工人的教育水平或另一个教育水平。

考虑：高能力工人选择一个教育水平e h ，低能力工人以概率π 选择e h ，以概率(1 – π) 选择e L 。

公司观察到e h 和e L 后的判断

μ(H |e h ) =

(1)q

q q π

+-

μ (H |e L ) = 0

公司对混同教育水平的工资

w h =

(1)q q q π+-y (H , e h ) +(1)(1)q q q π

π

-+-y (L , e h ), e ≥ e h

w (e ) = y (H , e ), e < e h

w

w p

w L *

e L * e h e s e

低能力工人随机选择的混同策略e h ，应当是与e L *无差异的 w L * – c (L , e L *) = w h – c (L , e h ) 由此解出

w h = r y (H , e h ) + (1 – r ) y (L , e h )

r = (1)q

q q π

+-

4.2.C 公司投资和资本结构 一个企业家为一个新项目融资.

现存公司的利润: π = L ，prob = p ; π= H , prob = 1- p 新项目投资: I ,

投资的收益: R

R > I (1 + r )

博弈的时间顺序: 自然决定利润: L 或 H 企业家观察 π 和提出股份 s , 投资者观察 s ，并选择拒绝还是接受

企业家的收益: 被拒绝：π, 被接受：(1-s )(π+R ) 投资者的收益: 拒绝：I (1 + r ), 接受：s (π+R )

投资者对π= L 的推断: q

他将接受 s 当且仅当

s [qL + (1 – q )H + R ] ≥ I (1 + r )

企业家偏好外部融资，当且仅当 π < (1- s )(π+R ), 即

s ≤

R

R

+π 如果

R

H p pL r I +-++)1()

1( ≤ s ≤ R H R +

混同均衡存在。

当p 很小，上式满足。当p 接近 1 则需满足

R L r I ++)1( ≤ s ≤ R

H R

+ R – I (1+r ) ≥ R

H

r I )1(+ - L

分离均衡:

当 π= L , 企业家提出 s = R

L r I ++)

1(, 投资者接受. 当 π = H , 企业家提出 s <

R

H r I ++)

1(, 投资者拒绝.

为何不取等号？

企业家用债券D融资:

收益: 如果不破产，π + R–D, 如果破产则为0.

投资者的收益: 企业不破产D, 破产π + R

混同均衡:

企业家提出D= I(1+r),

投资者接受。

4. 3精炼贝叶斯均衡的其它应用

4. 3.A 空谈博弈（Cheap-talk）

发送者的信号是口头信息

----无成本，无约束，无核查。

口头信息能传递信息的必要条件

1．不同的发送者类型有不同的偏好;

2. 接收者对不同行动的偏好依赖于发送者的类型;

3. 接收者与发送者对行动的偏好不是完全对立的.

博弈的时间顺序

1. 自然按照概率分布产生S的一个状态t i∈T

2. S观察t i，选择m j∈M

3. R观察m j，选择a k∈A

4. 收益为U S(t i, a k) 和U R(t i, a k)

混同均衡总是存在：接收者忽略任何信号。 接收者的最优行动 a * 求

A

a k

∈max ∑∈T

t i p ( t i ) U R (t i , a k ) 例: 分离均衡

发送者两个类型: T = {t L , t H }, Prob(t L ) = p 接收者两个行动: A = {a L , a H } 收益表：第1个数字为发送者收益。

S

t L t H

a L x ， 1 y ， 0

R

a H z , 0 w ， 1

不同的类型发送不同的信号，要求： 1．x 与z 的关系，与y 与w 的关系不同。 2。接收者的行动依赖于发送者类型。 3．x, z , w, y 的值与接收者的收益一致。 分离均衡存在: x ≥ z , w ≥ y

例 部分（partially ）混同均衡 发送者的类型空间: T = [0, 1], 均匀分布 接收者的行动空间: A = [0, 1] 收益: U S (t , a ) = –[a – (t + b )]2

U R (t , a ) = – (a – t ) 2

考虑 n 个信号:

[0, x 1 ), [ x 1, x 2), …, [x n -1, 1]

n =2: [0, x ), [x , 1]

发送者: [0, x ) → 0

接收者的推断: t 为[0, x ]上的均匀分布 接收者选择行动 a :

Max E U R (t , a ) = Max E[ – (a – t ) 2]

E[ – (a – t ) 2

] =?--x

dt x t a 0

21)(=x

1[(a – x ) 3 – a 3]

解出 a = x /2

发送者: [x , 1] → x

接收者的推断: t 为[x , 1]上的均匀分布 接收者选择行动 a :

Max E U R (t , a ) = Max E[ – (a – t ) 2]

E U R (t , a ) =E[ – (a – t ) 2

] =?---1

2

11

)(x

dt x

t a =

x

-11

[(a – 1) 3 – (a – x )3] 解出 a = (1 + x )/2

0 t 0 x t 1 1

发送者的收益:

发送0: U S 0(t , a ) = –[2

x – (t + b )]2 发送1: U S 1(t , a ) = –[

21x

+– (t + b )]2

均衡结果，在 x :

U S 0(x , a ) = U S 1(x , a )

–[2

x – (x + b )]2= –[2

1x

+– (x + b )]2 x =

21

– 2b 必要条件: b < 1/4。

n > 2的情形: [0, x 1), [ x 1, x 2), …, [x n -1, 1] 考虑第k 个边界: [x k -1, x k ), [x k , x k +1) 发送者: [x k -1, x k ) → x k -1 接收者的推断: 1/( x k - x k -1) 他的行动：a = (x k + x k -1 )/2

发送者: [x k , x k +1)→ x k 接收者的推断: 1/( x k +1 - x k ) 他的行动 a = (x k +1 + x k )/2

均衡结果，在 x k :

U Sk -1(x k , a ) = U Sk (x k , a )

–[(x k + x k -1 )/2– (x k + b )]2= –[(x k +1 + x k )/2– (x k + b )]2

x k -1 t k -1 t k x k +1

可以解出

x k +1 - x k = x k - x k -1 + 4b

类似可以得到

x k - x k-1 = x k -1 - x k -2 + 4b 因此

x k +1 - x k = x k - x k -1 + 4b

= x k -1 - x k -2 + 2? 4b = …= x 1 + k ?4b 则

1 = (1 - x n -1) + (x n -1 - x n -

2 ) + …+ (x 1 – 0) = x 1 + (n – 1)?4b + x 1 + (n – 2)?4b + … + x 1 = nx 1 +

2

)

1(-n n ?4b

必要条件: 2

)

1(-n n ?4b < 1 解出 21( 1 -b /21+) < n < 2

1

( 1+ b /21+)

4. 3. B 不对称信息下的序贯谈判（Sequential bargaining ）

一个企业和一个工会对工资谈判. 工会的保留工资: w r ，

企业的利润: π 为[πL ，πH ] 上的均匀分布. 简化：w r = πL = 0。

第1期，工会提出工资w 1，企业接受或拒绝。

如果企业拒绝，则第2期工会提出工资w 2，企业接受或拒绝。 如果企业拒绝，则结束。