平行四边形的存在性问题

平行四边形的存在性问题
专题攻略
解平行四边形的存在性问题一般分三步:
第一步寻找分类标准,第二步画图,第三步计算.
难点在于寻找分类标准,分类标准寻找的恰当,可以使得解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.
如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.
灵活运用向量和中心对称的性质,可以使得解题简便.
针对训练
1.如图,已知抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为P.若以A、C、P、M为顶点的四边形是平行四边形,求点M的坐标.
解析、由y=-x2-2x+3=-(x+3)(x-1)=-(x+1)2+4,
得A(-3,0),B(1,0),C(0,3),P(-1,4).
如图,过△P AC的三个顶点,分别作对边的平行线,三条直线两两相交的三个交点就是要求的点M.
①因为AM1//PC,AM1=PC,那么沿PC方向平移点A可以得到点M1.
因为点P(-1,4)先向下平移1个单位,再向右平移1个单位可以与点C(0,3)重合,所以点A(-3,0)先向下平移1个单位,再向右平移1个单位就得到点M1(-2,-1).
②因为AM2//CP,AM2=CP,那么沿CP方向平移点A可以得到点M2.
因为点C(0,3)先向左平移1个单位,再向上平移1个单位可以与点P(-1,4)重合,所以点A(-3,0)先向左平移1个单位,再向上平移1个单位就得到点M2(-4,1).
③因为PM3//AC,PM3=AC,那么沿AC方向平移点P可以得到点M3.
因为点A(-3,0)先向右平移3个单位,再向上平移3个单位可以与点C(0,3)重合,所以点P(-1,4)先向右平移3个单位,再向上平移3个单位就得到点M3(2,7).
2.如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
解析.由y=-x2+2x+3=-(x+1)(x-3),得A(-1,0),B(3,0).
①如图1,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P关于AB 的中点(1,0)对称,所以点M的横坐标为2.
当x=2时,y =-x2+2x+3=3.此时点M的坐标为(2,3).
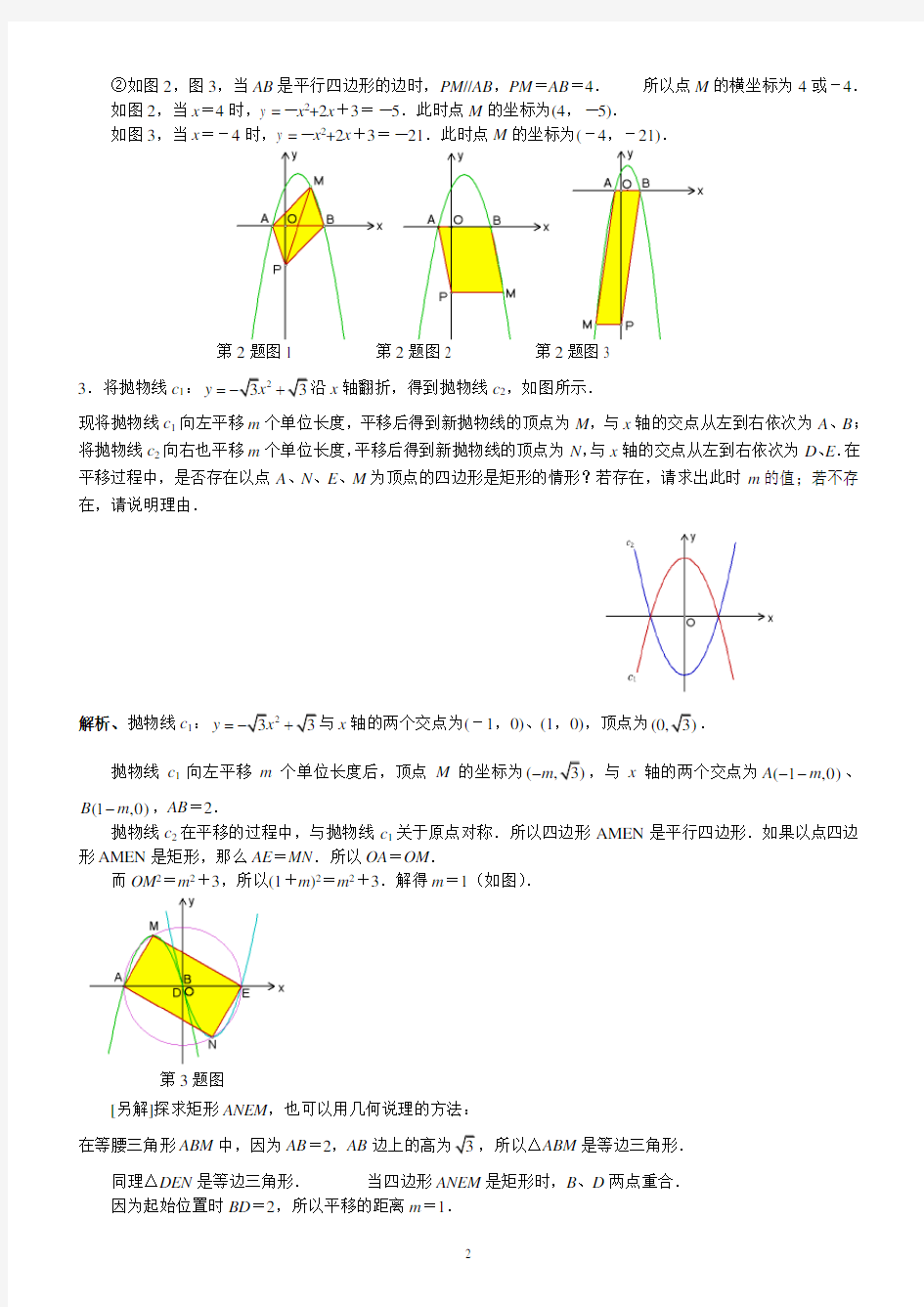
②如图2,图3,当AB是平行四边形的边时,PM//AB,PM=AB=4.所以点M的横坐标为4或-4.
如图2,当x=4时,y =-x2+2x+3=-5.此时点M的坐标为(4,-5).
如图3,当x=-4时,y =-x2+2x+3=-21.此时点M的坐标为(-4,-21).
第2题图1 第2题图2 第2题图3
3.将抛物线c1:2
y=+x轴翻折,得到抛物线c2,如图所示.
现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
解析、抛物线c1:2
y=x轴的两个交点为(-1,0)、(1,0),顶点为.
抛物线c1向左平移m个单位长度后,顶点M的坐标为(m
-,与x轴的两个交点为(1,0)
--、
A m
-,AB=2.
B m
(1,0)
抛物线c2在平移的过程中,与抛物线c1关于原点对称.所以四边形AMEN是平行四边形.如果以点四边形AMEN是矩形,那么AE=MN.所以OA=OM.
而OM2=m2+3,所以(1+m)2=m2+3.解得m=1(如图).
第3题图
[另解]探求矩形ANEM,也可以用几何说理的方法:
在等腰三角形ABM中,因为AB=2,AB ABM是等边三角形.
同理△DEN是等边三角形.当四边形ANEM是矩形时,B、D两点重合.
因为起始位置时BD=2,所以平移的距离m=1.
4.已知平面直角坐标系xOy (如图),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .
(1)求线段AM 的长; (2)求这个二次函数的解析式;
(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =
+的图像上,且四边形ABCD 是菱形,求点C 的坐标.
解析、(1)当x =0时,3334
y x =+=,所以点A 的坐标为(0,3),OA =3. 如图1,因为MO =MA ,所以点M 在OA 的垂直平分线上,点M 的纵坐标为
32. 将32y =代入32y x =,得x =1.所以点M 的坐标为3(1,)2
.因此AM =. (2)因为抛物线y =x 2+bx +c 经过A (0,3)、M 3(1,)2,所以3,31.2
c b c =???++=?? 解得52b =-,3c =.所以二次函数的解析式为2532
y x x =-+. (3)如图2,设四边形ABCD 为菱形,过点A 作AE ⊥CD ,垂足为E .
在Rt △ADE 中,设AE =4m ,DE =3m ,那么AD =5m . 因此点C 的坐标可以表示为(4m ,3-2m ).
将点C(4m ,3-2m )代入2532
y x x =-+,得23216103m m m -=-+. 解得12
m =或者m =0(舍去). 因此点C 的坐标为(2,2).
5.如图1,在Rt △ABC 中,∠C =90°,AC =6,BC =8,动点P 从点A 开始沿边AC 向点C 以每秒1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD //BC ,交AB 于点D ,联结PQ .点P 、Q 分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒(t ≥0).
(1)直接用含t 的代数式分别表示:QB =_______,PD =_______;
(2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值;若不存在,说明理由,并探究如何改变点Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度;
(3)如图2,在整个运动过程中,求出线段PQ 的中点M 所经过的路径长.
解析.(1)QB =8-2t ,PD =43
t . (2)当点Q 的速度为每秒2个单位长度时,四边形PDBQ 不可能为菱形.说理如下:
在Rt △ABC 中,AC =6,BC =8,所以AB =10.
已知PD //BC ,当PQ//AB 时,四边形PDBQ 为平行四边形.
所以
CQ CP CB CA =,即2686t t -=.解得125
t =. 此时在Rt △CPQ 中,245CQ =,2456sin 54CQ PQ CPQ ==?=∠. 所以2416855
BQ CB CQ =-=-
=,6BD PQ ==. 因此BQ ≠BD .所以四边形PDBQ 不是菱形.
如图1,作∠ABC 的平分线交CA 于P ,过点P 作PQ //AB 交BC 于Q ,那么四边形PDBQ 是菱形. 过点P 作PE ⊥AB ,垂足为E ,那么BE =BC =8.
在Rt △APE 中,23cos 5AE A AP t ===,所以103t =. 当PQ //AB 时,CQ CP CB CA =,即106386
CQ -=.解得329CQ =. 所以点Q 的运动速度为
3210169315
÷=. 第5题图1 (3)以C 为原点建立直角坐标系.
如图2,当t =0时,PQ 的中点就是AC 的中点E (3,0).
如图3,当t =4时,PQ 的中点就是PB 的中点F (1,4).
直线EF 的解析式是y =-2x +6.
如图4,PQ 的中点M 的坐标可以表示为(62t -,t ).经验证,点M (62t -,t )在直线EF 上. 所以PQ 的中点M 的运动路径长就是线段EF 的长,EF
=
第5题图2 第5题图3 第5题图4
[另解]第(3)题求点M 的运动路径还有一种通用的方法是设二次函数:
当t =2时,PQ 的中点为(2,2).
设点M 的运动路径的解析式为y =ax 2+bx +c ,代入E (3,0)、F (1,4)和(2,2),
得930,
4,42 2.a b c a b c a b c ++=??++=??++=?
解得a =0,b =-2,c =6.
所以点M 的运动路径的解析式为y =-2x +6.
6.如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|∶|OB|=1∶5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
(1)求此抛物线的函数表达式;
(2)设E是y轴右侧抛物线上异于点B的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为72?若存在,求出点M的坐标;若不存在,请说明理由.
解析(1)设OA的长为m,那么OB=OC=5m.由△ABC的面积S△ABC=15,得m=5.所以点A、B、C的坐标分别为(-1,0)、(5,0)、(0,-5).
设抛物线的解析式为y=a(x+1) (x-5),代入点C(0,-5),得a=1.
所以抛物线的解析式为y=(x+1) (x-5)=x2-4 x-5.
(2)抛物线的对称轴为直线x=2,设点E在对称轴右侧,坐标为(x,x2-4 x-5).
①如图1,当E在x轴上方时,EF=2(x-2),EH=x2-4 x-5.
解方程2(x-2)=x2-4 x-5,得310
x=+或310
x=-(舍去).
此时正方形的边长为2210
+.
②如图2,当E在x轴下方时,EF=2(x-2),EH=-(x2-4 x-5).
解方程2(x-2)=-(x2-4 x-5),得110
x=-(舍去).
x=+或110
此时正方形的边长为210.
第6题图1 第6题图2 第6题图3
(3)如图3,因为点B、C的坐标分别为(5,0)、(0,-5),所以BC与x轴正半轴的夹角为45°.
过点B作BM⊥BC,且使得BM=72
过点M作x轴的垂线,垂足为N,那么△BMN是等腰直角三角形.
在Rt△BMN中,斜边BM=72BN=MN=7.
因此点M的坐标为(-2,7)或(12,-7).
经检验,点(-2,7)在抛物线y=(x+1) (x-5)上;点(12,-7)不在这条抛物线上.
所以点M的坐标是(-2,7).
[另解]第(3)题也可以这样思考:
设抛物线上存在点M,设点M的坐标为(x,x2-4 x-5).
由于△BMN是等腰直角三角形,BN=MN,所以5-x=x2-4 x-5.
解得x=-2或x=5(与点B重合,舍去).所以点M的坐标是(-2,7).
这种解法不需要分情况讨论点M的位置,这是因为:
当M在点B的右侧时,方程为x-5=-(x2-4 x-5),这个方程和点M在点B的左侧时的方程是同一个方程.
7.如图1,在平面直角坐标系中,抛物线y =ax 2+bx -3a 经过A (-1,0)、B (0,3)两点,与x 轴交于另一点C ,顶点为D .
(1)求该抛物线的解析式及点C 、D 的坐标;
(2)经过点B 、D 两点的直线与x 轴交于点E ,若点F 是抛物线上一点,以A 、B 、E 、F 为顶点的四边形是平行四边形,求点F 的坐标;
(3)如图2,P (2,3)是抛物线上的点,Q 是直线AP 上方的抛物线上一动点,求△APQ 的最大面积和此时Q 点的坐标.
图1 图2
解析.(1)抛物线的解析式为y =-x 2+2x +3,C (3,0),顶点D (1,4).
(2)如图1,直线BD 为y =x +3,E (-3,0).
过△ABE 的三个顶点,分别作对边的平行线,三条直线两两相交,得到三个点F .
① 点E (-3,0)向左平移2个单位得到点A (-1,0),那么点B (0,3) 向左平移2个单位得到点F 1(2,3).经验
证,F 1(2,3)在抛物线上.
② F 2不在抛物线上.
③由B (0,3)先向下平移3个单位,再向左平移3个单位得到点E (-3,0),那么点A (-1,0) 先向下平移3个单位,再向左平移3个单位得到点F 3(-4,-3).经验证,F 3(-4,-3)不在抛物线上.
(3)如图2,直线AP 的解析式为y =x +1.过点Q 作y 轴的平行线交AP 于H .
设Q (x , -x 2+2x +3),那么H (x , x +1).
因此S △APQ =S △AQH +S △PQH =211()(2)322P A QH x x x x -=-++?23127()228x =--+
. 所以当12x =时,△APQ 的最大面积为827.此时Q )4
15,21(.
第7题图1 第7题图2
8.已知抛物线2(2)y a x b =-+ (0)ab <的顶点为A ,与x 轴的交点为B ,C (点B 在点C 的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC 为直角三角形,求a ,b 的值;
(3)若D 为抛物线对称轴上一点,则以A 、B 、C 、D 为顶点的四边形能否为正方形?若能,请求出a ,b 满足的关系式;若不能,说明理由.
解析(1)抛物线对称轴是直线x =2. (2)点B (0,0)关于对称轴x =2对称的点C 为(4,0),设抛物线的解析式为y =ax (x -4).
当△ABC 为直角三角形时,△ABC 为等腰直角三角形,AB =AC ,∠BAC =90°.
所以点A 的坐标为(2,2)或(2,-2).
①将A (2,2)代入y =ax (x -4),得1
2
a =-.于是211(4)222y x x x x =--=-+.因此2
b =. ②当A (2,-2)代入y =ax (x -4),得12
a =.于是211(4)222y x x x x =-=-.因此2
b =-.
(3)如果四边形ABDC是正方形,那么A、D关于BC(x轴)对称且△ABC为等腰直角三角形.由A(2,b),得B(2+b,0)、C(2-b,0).
于是可得抛物线的解析式为y=a(x-2-b)(x-2+b).
代入A(2,b),得b=-ab2.所以1
ab=-.
9.如图,已知双曲线
6
y
x
=与直线AB交于A、B两点,与直线CD交于C、D两点.
(1)求证四边形ACBD是平行四边形;
(2)四边形ACBD可能是矩形吗?可能是正方形吗?
(3)如果点A的横坐标为3,点C的横坐标为m(m>0),四边形ACBD的面积为S,求S与m的之间的关系式.
解析.(1)因为A、B关于原点O对称,C、D关于原点O对称,所以OA=OB,OC=OD.所以四边形ACBD是平行四边形.
(2)如图1,当直线AB与直线CD关于直线y=x对称时,OA=OB=OC=OD,所以四边形ACBD可以成为矩形.
因为x≠0,y≠0,所以点A、B、C、D不可能落在坐标轴上,因此直线AB与CD不可能垂直,即平行四边形ACBD的对角线不可能互相垂直,所以四边形ACBD不可能成为正方形.
(3)如图2,作AE⊥x轴于E,CF⊥x轴于F,那么S△AOE=S△COF.
①如图2,当点C在点A上方时,设OA与CF交于点M,那么S四边形AEFM=S△COM.
因此S△AOC=S梯形AEFC=169
(2)(3)
2
m m
m m
+-=-.
所以S=S平行四边形ACBD=4S△AOC
36
4m m
=-.
②如图3,当点C在点A下方时,S△AOC=S梯形AEFC=169 (2)(3)
2
m m
m m
+-=-.
所以S=S平行四边形ACBD=4S△AOC
36
4m
m
=-.
第9题图1 第9题图2 第9题图3
小专题(三) 特殊平行四边形中的最值问题
小专题(三)特殊平行四边形中的最值问题 【例】(盐城中考)如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线 段AB、AD、 AC上.已知EP=FP=4,EF=43,∠BAD=60°,且AB>4 3. (1)求∠EPF的大小; (2)若AP=6,求AE+AF的值; (3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值. 【思路点拨】(1)求∠EPF的大小,就是解△EFP,通过作底边上的高转化为直角三角形解决;(2)这里∠BAD+∠EPF=180°,PE=PF,可通过构造全等三角形解决问题;(3)观察图形,作PM⊥AB 于M,AP的长随PM大小的变化而变化. 【方法归纳】动态图形中最值问题关键要改变思考的角度,善于转化为另一个量的最值问题考虑. 1.如图,∠MON=90°,矩形ABCD的顶点A,B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离是多少?
2.以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B 两点,求线段AB的最小值.
参考答案 【例】(1)过点P 作PG ⊥EF ,垂足为G. ∵PE =PF ,PG ⊥EF ,∴FG =EG =23,∠FPG =∠EPG =12 ∠EPF. ∵EP =4,∴在Rt △FPG 中,由勾股定理得PG =2.∴PG =12 PF.∴∠PFG =30°.∴∠FPG =60°.∴∠EPF =2∠FPG =120°. (20作PM ⊥AB ,PN ⊥AD ,垂足分别为M 、N.在菱形ABCD 中,∠DAC =∠BAC , ∴点P 到AB 、AD 两边的距离相等,即PM =PN. ∵在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF , ∴Rt △PME ≌Rt △PNF.∴FN =EM. 在Rt △PMA 中,∠PMA =90°,∠PAM =12 ∠DAB =30°,∴AM =3 3. 同理:AN =3 3.∴AE +AF =(AM -EM)+(AN +NF)=AM +AN =6 3. (3)当EF ⊥AC ,点P 在EF 右侧时,AP 有最大值, 当EF ⊥AC ,点P 在EF 左侧时,AP 有最小值.故AP 的最大值为8,AP 的最小值为4. 针对训练 1.取AB 的中点E ,连接OE 、DE 、OD , ∵OD ≤OE +DE ,∴当O 、D 、E 三点共线时,点D 到点O 的距离最大. ∵AB =2,BC =1,∴OE =AE =12 AB =1,DE =AD 2+AE 2=12+12= 2. ∴OD 的最大值为2+1. 2.∵四边形CDEF 是正方形,∴∠OCD =∠ODB =45°,∠COD =90°,OC =OD. ∵AO ⊥OB ,∴∠AOB =90°.∴∠COA +∠AOD =90°,∠AOD +∠DOB =90°.∴∠COA =∠DOB. ∵在△COA 和△DOB 中,?????∠OCA =∠ODB ,OC =OD ,∠AOC =∠BOD , ∴△COA ≌△DOB.∴OA =OB. ∵∠AOB =90°, ∴△AOB 是等腰直角三角形. 由勾股定理得AB =OA 2+OB 2=2OA ,要使AB 最小,只要OA 取最小值即可, 根据垂线段最短,OA ⊥CD 时,OA 最小, ∵四边形CDEF 是正方形, ∴FC ⊥CD ,OD =OF =OC. ∴CA =DA. ∴OA =12 CF =1.∴ AB = 2. ∴AB 的最小值为 2.
平行四边形性质和判定习题(答案详细)
平行四边形性质和判定习题 1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F. (1)求证:BE=DF; (2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由). 2.如图所示,?AECF的对角线相交于点O,DB经过点O,分别与AE, CF交于B,D. 求证:四边形ABCD是平行四边形. 3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足 分别为E,F. (1)求证:△ABE≌△CDF; (2)若AC与BD交于点O,求证:AO=CO. 4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD. 5.如图,已知D是△ABC的边AB上一点,CE∥AB, DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系, 并加以证明. 6.如图,已知,?ABCD中,AE=CF,M、N分别是DE、BF的中点. 求证:四边形MFNE是平行四边形.
7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA. 求证:四边形AECF是平行四边形. 8.在?ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形. 9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE. 10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形? 11.如图:已知D、E、F分别是△ABC各边的中点, 求证:AE与DF互相平分. 12.已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四 边形.求证:四边形ABOE、四边形DCOE都是平行四边形.
二次函数平行四边形存在性问题例题
二次函数平行四边形存在性问题例题 一.解答题(共9小题) 1.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点. (1)求抛物线的解析式; (2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标; (3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 2.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧). (1)求抛物线的解析式及点B坐标; (2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值; (3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. 3.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点
分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x 轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F 在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由. 4.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA ﹣QO|的取值范围. 5.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,
平行四边形的存在性问题
平行四边形的存在性问题 【真题典藏】 1.(2008年青浦区第24题)如图1,在平面直角坐标系中,点O 是坐标原点,正比例函数kx y =(x 为自变量)的图像与双曲线x y 2 - =交于点A ,且点A 的横坐标为2-. (1)求k 的值. (2)将直线kx y =(x 为自变量)向上平移4个单位得到直线BC ,直线BC 分别交x 轴、y 轴于B 、 C ,如点 D 在直线BC 上,在平面直角坐标系中求一点P ,使以O 、B 、D 、P 为顶点的四边形是菱形. 图1 图2 2.(2009年普陀区第25题)如图2,在平面直角坐标系xOy 中,O 为原点,点A 、C 的坐标分别为(2, 0)、(1,33). 将△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置,抛物线x ax y 322 -=经 过点A ,点D 是该抛物线的顶点. (1)求证:四边形ABCO 是平行四边形; (2)求a 的值并说明点B 在抛物线上; (3)若点P 是线段OA 上一点,且∠APD =∠OAB ,求点P 的坐标; (4)若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点在y 轴上,写出点P 的坐标. 3.(2010年上海市第24题)参见《考典40 几何计算说理与说理计算问题》第3题. 4.(2011年上海市第24题)已知平面直角坐标系xOy (如图3),一次函数3 34 y x =+的图像与y 轴交于点A ,点M 在正比例函数3 2 y x = 的图像上,且MO =MA .二次函数 y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长; (2)求这个二次函数的解析式;
专题 平行四边形的性质与判定(学生版)
专题 平行四边形的性质与判定 【能力提升】 例1.如图已知△ABC ,分别以△ABC 的三边为边在△ABC 的同侧作三个等边三角形:△ABE .△BCD .△ACF ,求证:四边形DEAF 是平行四边形. 例2.(1)如图,在平行四边形ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,若AE =4,AF =6,AD +CD =20,则平行四边形ABCD 的面积为 . (2)在平面直角坐标系中,以O (0,0),A (1,1),B (3,0),C 为顶点构造平行四边形,请你写出满足条件的点C 坐标为 . 例3.一个六边形的六个内角都是120°(如图),连续四条边的长依次为 1,3,3,2,则这个六边形的周长是_______. 例4.如图,Rt △ABC 中,∠C =90°,点D 、点E 为边AB 上的点,且AD =BE ,点M 、N 分别为边AC 、BC 上的点.已知:AB =a ,DE =b ,则四边形DMNE 的周长的最小值为 . 例5.如图,平行四边形ABCD 中,AB =8cm ,AD =12cm ,点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动,点Q 在BC 边上,以每秒4cm 的速度从点C 出发,在CB 间往返运动,两个点同时出发,当点P 到达点D 时停止(同时点Q 也停止),在运动以后,以P 、D 、Q 、B 四点组成平行四边形的次数有多少次?
例6.理论探究:已知平行四边形ABCD的面积为100,M是AB所在直线上一点. (1)如图1:当点M与B重合时,S△DCM=; (2)如图2,当点M与B与A均不重合时,S△DCM=; (3)如图3,当点M在AB(或BA)的延长线上时,S△DCM=; 拓展推广:如图4,平行四边形ABCD的面积为a,E、F分别为DC、BC延长线上两点,连接DF、AF、AE、BE,求出图中阴影部分的面积,并说明理由. 实践应用:如图5是我市某广场的一平行四边形绿地ABCD,PQ、MN分别平行于DC、AD,它们相交于点O,其中S四边形AMOP=300m2,S四边形MBQO=400m2,S四边形NCQO=700m2,现进行绿地改造,在绿地内部作一个三角形区域MQD(连接DM、QD、QM,图中阴影部分)种植不同的花草,求出三角形区域的面积.
八年级数学平行四边形中的最值问题专练
八年级数学平行四边形中的最值问题专练 一、选择题 1.如图,将两张长为8,宽为2的长方形纸条交叉,使重叠部分是一个菱形(四条边相 等),容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是() A. 17 B. 16 C. 8√2 D. 2√17 2.如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正 方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为() A. √3+1 B. 2√3?1 C. 3 D. 4?√3 3.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边 ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为() A. √2+1 B. √5 C. √145 5 D. 5 2 4.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC=4√3,BC的中点为D. 将△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,连 接DG.在旋转过程中,DG的最大值是() A. 4 B. 6 C. 2+2√3 D. 8 5.如图,正方形ABCD,边长为2,E是边BC上的一动点,连DE,取DE中
点G,将GE绕E顺时针旋转90°到EF,连接CF。则CF的最小值为() A. √5 5B. 2 5 √5 C. 2 D. 1 6.如图,在边长为4的正方形ABCD中,E是AB边上的一点, 且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最 小值为() A. 5 B. 6 C. 4√2 D. 8 7.如图,在平行四边形ABCD中,∠C=120°,AD= 2AB=4,点H、G分别是边AD、BC上的动点.连 接AH、HG,点E为AH的中点,点F为GH的中 点,连接EF.则EF的最大值与最小值的差为() A. 1 B. √3?1 C. √3 2 D. 2?√3 二、填空题 8.如图,在菱形ABCD中,∠ABC=120°,AB=6, 点E在边AB上,且AE=2,P是对角线AC上的一 个动点,则PB+PE的最小值是______. 9.点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°,点M, N分别是AB,BC边上的中点,则△MPN的周长最小值是_______________.
ZBP平行四边形存在性问题之两定两动.doc
学习必备欢迎下载 问题 1:存在性问题的处理框架是什么? 问题 2:两定两动的平行四边形存在性问题的分类标准是什么? 1. 如图,将矩形OABC 放置在平面直角坐标系中,OA=8, OC=12,直线与x 轴交于点D,与 y 轴交于点E,把矩形沿直线DE翻折,点 O 恰好落在AB 边上的点 F 处,M 是直线 DE 上的一个动点,直线DF 上是否存在点N,使以点 C,D,M ,N 为顶点的四边形是平行四边形?则符合题意的点N 的坐标是? 2.如图,在平面直角坐标系中,直线与交于点A,与x 轴分别交于 点 B 和点 C, D 是直线 AC上一动点, E 是直线AB 上一动点.若以O, D, A,E 为顶点的四边形是平行四边形,则点 E 的坐标为? 反思与总结: 问题 1:平行四边形存在性问题的处理框架中第一步:研究背景图形,需要研究哪些内容? 问题 2:画出对应图形后求解点坐标的套路是什么?
练习 1.如图,直线与 x 轴、 y 轴分别交于A, B 两点,直线BC x 轴交于点C,且 与 ∠ABC=60°,若点 D 在直线AB 上运动,点E在直线 BC 上运动,且以O, B, D,E 为顶点的 四边形是平行四边形,则点 D 的坐标为 ( ) 2..如图,在平面直角坐标系中,矩形OABC的对角线AC=12,∠ ACO=30°,把矩形沿直线 DE 翻折,使点 C 落在点 A 处, DE 与 AC 相交于点 F,若点 M 是直线 DE上一动点,点N 是直线 AC 上一动点,且以O,F,M , N 为顶点的四边形是平行四边形,则点N 的坐标为 () 3.如图,直线分别交x轴、y轴于A,B两点,线段AB 的垂直平分线交x 轴于 点 C,交 AB 于点 D.若在平面内存在点 E,使得以点 A,C,D,E 为顶点的四边形是平行四边 形,则点 E 的坐标为
平行四边形的性质与判定解题技巧专题练习含答案
综合滚动练习:平行四边形的性质与判定 时间:45分钟分数:100分得分:________ 一、选择题(每小题4分,共32分) 1.在?ABCD中,若∠A+∠C=120°,则∠A的度数是() A.100°B.120°C.80°D.60° 2.如图,在?ABCD中,点O是对角线AC,BD的交点,下列结论错误的是() A.AB∥CD B.AB=CD C.AC=BD D.OA=OC 第2题图第5题图 3.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的值可以是() A.4∶3∶3∶4 B.7∶5∶5∶7 C.4∶3∶2∶1 D.7∶5∶7∶5 4.平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是() A.(-2,1) B.(-2,-1) C.(-1,-2) D.(-1,2) 5.如图,?ABCD中,点E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为() A.BE=DF B.BF=DE C.AE=CF D.∠1=∠2 6.如图,在?ABCD中,BF平分∠ABC交AD于点F,CE平分∠BCD交AD于点E.若AB=6,EF=2,则BC的长为() A.8 B.10 C.12 D.14 第6题图第7题图 7.如图,在?ABCD中,∠B=80°,AE平分∠BAD交BC于E,CF∥AE交AD于F,则∠BCF等于() A.40°B.50°C.60°D.80° 8.(2017·龙东中考)在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是() A.22 B.20 C.22或20 D.18 二、填空题(每小题4分,共24分)
中考真题解析分类汇编之平行四边形的判定
平行四边形的判定 全国中考真题解析分类汇编 一、选择题 1. (郴州)如图,下列四组条件中?不能判定四边形ABCD是平行四边形的是 () A、AB=DC , AD=BC B、AB // DC , AD // BC C、AB // DC, AD=BC D、AB // DC , AB=DC 考点:平行四边形的判定。 分析:平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边 形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形. 解答:根据平行四边形的判定,A、B、D均符合是平行四边形的条件,C则不能判定是平行四边形. 故选:C. 点评:此题主要考查了学生对平行四边形的判定的掌握情况. 对于判定定理:一组 对边平行且相等的四边形是平行四边形.”应用时要注意必须是一组”而一组对边 平行且另一组对边相等”的四边形不一定是平行四边形. 2. (泰州)四边形ABCD中,对角线AC、BD相交于点0,给出下列四组条件: ①AB // CD, AD // BC;②AB=CD , AD=BC ; @A0=C0 , B0=D0 ;@AB // CD, AD=BC ?其中一定能判断这个四边形是平行四边形的条件共有() A、1组 B、2组 C、3组 D、4组 考点:平行四边形的判定。
专题:几何综合题。 分析:根据平行四边形的判断定理可作出判断. 解答:①根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形; ②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形; ③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形; ④根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,可知④不能判断这个四边形是平行四边形; 故给出下列四组条件中,①②③能判断这个四边形是平行四边形,故选:C, 点评:此题主要考查了平行四边形的判定定理,准确无误的掌握定理是做题的关键. 3. (柳州)如图,在平行四边形ABCD中,EF// AD,HN// AB,则图中的平行四边形的个数共有() C、7个 D、5个 考点:平行四边形的判定与性质。 专题:证明题。 分析:根据根据平行四边形的定义即可求解. 解答:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边DEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF 和ABCD都是平行四边形,共9个. 故选B. 点评:此题考查的知识点是平行四边形的判定和性质,本题可根据平行四边形的定
一次函数之平行四边形存在性问题
一次函数与平行四边形 1.线段中点公式 平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2), 则线段AB 的中点P 的坐标为 (2,22121y y x x ++) 例:如图,已知点A (-2,1),B (4,3),则线段AB 的中点P 的坐标是________. 2.线段的平移 平面内,线段AB 平移得到线段A'B' ,则①AB ∥A'B' ,AB =A'B' ;②AA'∥BB',AA'= BB'. 如图,线段AB 平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________. 例:如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)、D (x 4,y 4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标? 例:如图,已知□ABCD 中A (-2,2),B (-3,-1), C (3,1),则点D 的坐标是________. 方法一:利用线段平移 总结:x 1-x 2= x 4-x 3,y 1-y 2= y 4-y 3 或者 x 4-x 1= x 3-x 2,y 4-y 1= y 3-y 2 等 方法二:利用中点公式 总结:x 1+x 3= x 2+x 4,y 1+y 3= y 2+y 4
类型一:三定一动 例1 、如图,平面直角坐标中,已知中A (-1,0),B (1,-2),C (3,1),点D是平面内一动点,若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是_________________________________. 总结:三定一动问题,可以通过构造中点三角形得以解决. 说明:若题中四边形ABCD是平行四边形,则点D的坐标只有一个结果________
《平行四边形判定》专题复习
6月27日:专题复习(一)——《平行四边形判定》 姓名:___________班别_____________ A 组: 1、四边形中,有两条边相等,且另两条边也相等,则这个四边形( ) A 、一定是平行四边形 B 、一定不是平行四边形 C 、可能是平行四边形 D 、以上答案都错 2、以不在同一直线上的三个点为顶点作平行四边形,最多能作( ) A 、4个 B 、3个 C 、2个 D 、1个 3、如图,□ABCD 中, E , F 分别为AD ,BC 边上的一点,若再增加一个条件__________,就可推得BE=DF 4、 如图,在等腰梯形ABCD 中,AB ∥CD ,AD=BC ,延长AB 使 BE=DC ,试说明 (1)四边形DBEC 是平行四边形(2)AC=CE 5、如图,在平行四边形ABCD 中,BF DE =. 求证:四边形AFCE 是平行四边形. 6、如图,E F ,是平行四边形ABCD 对角线BD 上的两点,给出下列三个条件: ①BE DF =;②AEB DFC =∠∠;③AF EC ∥. 请你从中选择一个适当的条件 . 使四边形AECF 是平行四边形,并证明你的结论. E F
B 组: 1、平面直角坐标系中,点A (-2,5),B (-3,-1)C (1,-1),在第一象限内找一点D ,使得四边形ABCD 是平行四形,那么点D 的坐标是______________。 2、如右图,在□ABCD 中,AD=5,AB=3,AE 平分∠BAD 交BC 边于点 E ,则线段BE 、EC 的长度分别为( ) A 、2和3 B 、3和2 C 、4和1 D 、1和4 3、14.如图,□ABCD 中,EF 过对角线的交点O ,AB =4,AD =3, OF =1.3,则四边形BCEF 的周长为( ) A.8.3 B.9.6 C.12.6 D.13.6 4、A 、B 、C 、D 在同一平面内,从①AB ∥CD ;②AB =CD ;③BC =AD ;④BC ∥AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有( ) A .3种 B .4种 C .5种 D .6种 4、如图:BD 是□ABCD 的对角线,AE ⊥BD 于E ,CF ⊥BD 于F ,求证:四边形AECF 为平行四边形. 5、 如图,△ABC 中,D 是AB 的中点,E 是AC 上的点,且∠ABE=∠BAC ,EF ∥AB , DF ∥BE 。(1)猜想DF 与AE 有怎样的关系(2)证明你的猜想 6、如图3,田村有一口呈四边形的池塘,在它的四个角A 、B 、C 、D 处均种有一棵大核桃树.田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形的形状,请问田村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法). F
平行四边形的存在性问题
平行四边形的存在性问题 专题攻略 解平行四边形的存在性问题一般分三步: 第一步寻找分类标准,第二步画图,第三步计算. 难点在于寻找分类标准,分类标准寻找的恰当,可以使得解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点. 如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况. 灵活运用向量和中心对称的性质,可以使得解题简便. 针对训练 1.如图,已知抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为P.若以A、C、P、M为顶点的四边形是平行四边形,求点M的坐标. 解析、由y=-x2-2x+3=-(x+3)(x-1)=-(x+1)2+4, 得A(-3,0),B(1,0),C(0,3),P(-1,4). 如图,过△P AC的三个顶点,分别作对边的平行线,三条直线两两相交的三个交点就是要求的点M. ①因为AM1//PC,AM1=PC,那么沿PC方向平移点A可以得到点M1. 因为点P(-1,4)先向下平移1个单位,再向右平移1个单位可以与点C(0,3)重合,所以点A(-3,0)先向下平移1个单位,再向右平移1个单位就得到点M1(-2,-1). ②因为AM2//CP,AM2=CP,那么沿CP方向平移点A可以得到点M2. 因为点C(0,3)先向左平移1个单位,再向上平移1个单位可以与点P(-1,4)重合,所以点A(-3,0)先向左平移1个单位,再向上平移1个单位就得到点M2(-4,1). ③因为PM3//AC,PM3=AC,那么沿AC方向平移点P可以得到点M3. 因为点A(-3,0)先向右平移3个单位,再向上平移3个单位可以与点C(0,3)重合,所以点P(-1,4)先向右平移3个单位,再向上平移3个单位就得到点M3(2,7). 2.如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标. 解析.由y=-x2+2x+3=-(x+1)(x-3),得A(-1,0),B(3,0). ①如图1,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P关于AB 的中点(1,0)对称,所以点M的横坐标为2. 当x=2时,y =-x2+2x+3=3.此时点M的坐标为(2,3).
二次函数中的平行四边形存在性问题
二次函数中的平行四边形存在性问题 目标:1、通过本节课的学习,提高学生分析问题,解决问题的能力。 2、能总结出解决平行四边形存在性问题的一般方法和思路。重点:解决平行四边形存在性问题的一般方法及思路。 难点:根据条件求平行四边形的顶点坐标。 过程: 一、复习 1、平行四边形的性质 角: 边; 对角线: 2、二次函数的相关知识点 表达式、顶点坐标、对称轴、增减性 二、探索新知 1、単动点(知3点求1点) (1)已知平面上有不在同一条直线上的三点A、B、C,点D是平面上任一点,若此四点能构成平行四边形则符合条件的D点有几个? ()
学生画图说明 思考:如何找第四点?找第四点的方法? (2)类题 (1)已知抛物线与坐标轴分别交于A(-1、0)、B (3、0)、C (0、3)三点,能否在平面内在找一点D使得它们四点围成的四边形为平行四边形? 学生分析总结规律、思路。 ①、根据平行四边形的边、对角线的性质(对边平行且相等, 对角线互相平分)我们可以选择一种情况作为画图的依据。 ②、在求点的坐标时(以边为例)我们先满足对边平行再用对 边相等求出要求的点的坐标。
2、 双动点(知2点求2点) (1) 学生再次画图说明(给出两点画出另外两点) (2)类题 如图,抛物线y= 13 x 2-mx+n 与x 轴交于A 、B 两点,与y 轴交于点C (0.-1).且对称轴x=l . ① 求出抛物线的解析式及A 、B 两点的坐标; ② 点Q 在y 轴上,点P 在抛物线上,要使Q 、P 、A 、B 为顶点的四边形是平行四边形,请求出所有满足条件的点P 的坐标。
点A,点B是定点 点P,点Q是动点 分两种情况:AB为边,AB为对角线 3、小结 4、布置作业 5、
平行四边形存在性问题
平行四边形存在性问题 一、解平行四边形的存在性问题一般分三个步骤 第一步寻找分类标准,第二步画图,第三步计算. 二、难点在于寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复不遗漏,也可以使计算又准又快. 三、如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点,利用横纵坐标的平移变化得出结论。 四、如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况,灵活运用向量和中心对称的性质,可以使得解题简便。(辅助手段~三角形全等,等积法,中点坐标公式) 例1.已知抛物线 b ax ax y ++-=22 与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C . ⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式; ⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由. 例2、如图,抛物线:y= x 2﹣x ﹣ 与x 轴交于A 、B (A 在B 左侧),A (﹣1,0)、B (3,0),顶点为C (1,﹣2)(1)求过A 、B 、C 三点的圆的半径.(2)在抛物线上找点P ,在y 轴上找点E ,使以A 、B 、P 、E 为顶点的四边形是平行四边形,求点P 、E 的坐标. 例 3.已知,如图抛物线
23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。点B 的坐标为(1,0),OC=30B .(1)求抛物线的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值: (3)若点E 在x 轴上,点P 在抛物线上。是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由. 例4.已知抛物线:x x y 22 12 1+- = (1)求抛物线1y 的顶点坐标. (2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y 的解析式. (3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、 N 四点构成以OP 为一边的平行四边形, 若存在,求出N 点的坐标;若不存在,请说明理由. 例5.如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2. (1)求A 、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理 x y y 12 3 4 5 6 7 8 9 54321 -1-2-3-4 1 y 2 -1
平行四边形的判定专题练习题
平行四边形的判定练习 1.如图,?已知AD?∥BC,?要使四边形ABCD?为平行四边形,?需要添加的条件是_______.(只需填写 一个) 2. 在四边形ABCD中,AB∥CD,∠A=∠C,求证:四边形ABCD是平行四边形. 3.已知:如图,在四边形ABCD中,对角线AC和BD交于点O,且OA=OC,AB∥ 形ABCD是平行四边形。 4.如图,已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD?是平行四边形.5、如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF,AE与CF相等吗?说明理由. 6.如图,已知四边形ABCD和四边形AEFD都是平行四边形,求证:四边形BCFE?是平行四边形.7.有一个四边形的四边长分别是a,b,c,d,且有a2+b2+c2+d2=2(ac+bd). 求证:此四边形是平行四边形. D A C O
8.如图,已知ABCD ,E ,F 是对角线BD 所在直线上的两点,且AE ∥CF ,求证:CE ∥AF . 9.□ABCD 中,AC 、BD 交于点O ,AE=CF ,求证:BE=DF 10.(变式练习1)如图,已知ABCD 中,对角线AC ,BD 交于点O ,点E ,F ,G ,H 分别是OB ,OC ,OD ,OA?的中点,求证:四边形EFGH 是平行四边形. 11、(变式练习2)□ABCD 中,AC 、BD 交于点O ,AE=CF ,BM=DN 求证:四边形MFNE 是平行四边形 12. (变式练习3)如图,平行四边形ABCD 中,E 、F 是AC 上两点,且AE=CF ,又点M 、N 分别在AB 、CD 上,且MF ∥EN ,MN 交AC 于O 。求证:EF 与MN 互相平分。 13、(变式练习4)如图所示,□ABCD 的对角线AC 、BD 交于O ,EF 过点O 交AD 于E ,交BC 于F ,G 是OA 的中点,H 是OC 的中点,四边形EGFH 是平行四边形,说明理由. 14. □ABCD 中,E 、F 分别是边AD 、BC 上的点,请你自行规定E 、F 在边AD 、BC 上的位置,然后补充题设、提出结论并证明(要求:至少编制两个正确的命题,且补充题设不能相同). N M F E O A F E O A
平行四边形存在性问题
平行四边形存在性问题 1.如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在x轴、y轴上,且OA、OB的长满足方程x2﹣16x+64=0. (1)求点A、B的坐标; (2)将点A翻折落在线段OB的中点C处,折痕交OA于点D,交斜边于点E,求直线DE的解析式; (3)在(2)的条件下,在平面直角坐标系内,是否存在点F使点A、D、E、F为顶点的四边形是平行四边形?若存在请直接写出点F的坐标;若不存在,请说明理由. 2.如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止. (1)若动点M、N同时出发,经过几秒钟两点相遇? (2)在相遇前,是否存在过点M和N的直线将?ABCD的面积平分?若存在,请求出所需时间;
若不存在,请说明理由. (3)若点E在线段BC上,BE=2cm,动点M、N同时出发且相遇时均停止运动,那么点M运动到第几秒钟时,与点A、E、N恰好能组成平行四边形? 3.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处. (1)如图,已知折痕与边BC交于点E,连结AP、EP、EA.求证:△ECP∽△PDA; (2)若△ECP与△PDA的面积比为1:4,求边AB的长; (3)在(2)的条件下以点A为坐标原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,问在坐标平面内是否存在点M,使得以点A、B、E、M为顶点的四边形是平行四边形?若存在请直接写出点M的坐标;若不存在请说明理由.
特殊的平行四边形专题(题型详细分类)
特殊的平行四边形讲义 知识点归纳 矩形,菱形和正方形之间的联系如下表所示: 四边形分类专题汇总 专题一:特殊四边形的判定 【知识点】 1.平行四边形的判定方法: (1)______________ (2)______________ (3)______________ (4)______________ (5)______________ 2.矩形的判定方法: (1)______________ (2)______________ (3)______________ 3.菱形的判定方法: 矩形菱形正方形 性 质 边对边平行且相等对边平行,四边相等对边平行,四边相等 角四个角都是直角对角相等四个角都是直角 对 角 线 互相平分且相等 互相垂直平分,且每条对 角线平分一组对角 互相垂直平分且相等,每条对角线平分一组对角判定 ·有三个角是直角; ·是平行四边形且有 一个角是直角; ·是平行四边形且两 条对角线相等. ·四边相等的四边形; ·是平行四边形且有一组 邻边相等; ·是平行四边形且两条对 角线互相垂直。 ·是矩形,且有一组邻边相等; ·是菱形,且有一个角是直角。 对称性既是轴对称图形,又是中心对称图形
(1)______________ (2)______________ (3)______________ 4.正方形的判定方法: (1)______________ (2)______________ (3)______________ 5.等腰梯形的判定方法: (1)______________ (2)______________ (3)______________ 【练一练】 一.选择题 1.能够判定四边形ABCD是平行四边形的题设是(). A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D C.AB=CD,AD=BC D.AB=AD,CB=CD 2.具备下列条件的四边形中,不能确定是平行四边形的为(). A.相邻的角互补B.两组对角分别相等 C.一组对边平行,另一组对边相等D.对角线交点是两对角线中点 3.下列条件中,能判定四边形是平行四边形的条件是( ) A.一组对边平行,另一组对边相等 B.一组对边平行,一组对角相等 C.一组对边平行,一组邻角互补 D.一组对边相等,一组邻角相等 4.如下左图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是().A.若AO=OC,则ABCD是平行四边形; B.若AC=BD,则ABCD是平行四边形; C.若AO=BO,CO=DO,则ABCD是平行四边形; D.若AO=OC,BO=OD,则ABCD是平行四边形 5.不能判定四边形ABCD是平行四边形的条件是() A.AB=CD,AD=BC B.AB∥CD,AB=CD C.AB=CD,AD∥BC D.AB∥CD,AD∥BC 6.四边形ABCD的对角线AC,BD相交于点O,能判断它为矩形的题设是() A.AO=CO,BO=DO B.AO=BO=CO=DO C.AB=BC,AO=CO D.AO=CO,BO=DO,AC⊥BD 7.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是() A.AB=CD B.AD=BC C.AB=BC D.AC=BD 8.在四边形ABCD中,O是对角线的交点,下列条件能判定这个四边形是正方形的是() A、AC=BD,AB∥CD,AB=CD B、AD∥BC,∠A=∠C C、AO=BO=CO=DO,AC⊥BD D、AC=CO,BO=DO,AB=BC 9.在下列命题中,真命题是() A.两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形 C.两条对角线互相平分的四边形是平行四边形 D.两条对角线互相垂直且相等的四边形是正方形 10.在下列命题中,正确的是() A一组对边平行的四边形是平行四边形B有一个角是直角的四边形是矩形 C有一组邻边相等的平行四边形是菱形D对角线互相垂直平分的四边形是正方形
特殊平行四边形动点及存在性问题压轴题终审稿)
特殊平行四边形动点及存在性问题压轴题 文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-
特殊平行四边形中的动点及存在性问题 【例1】正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为。 【练习1】如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点. (1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标; (2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F 的坐标. 【例2】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当三角形△ODP是腰长为5的等腰三角形时,P的坐标为; 【练习2】如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0), 并且a,b满足16 b=.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒) (1)求B、C两点的坐标; (2)当t为何值时,四边形PQCB是平行四边形?并求出此时P、Q两点的坐标; (3)当t为何值时,△PQC是以PQ为腰的等腰三角形?并求出P、Q两点的坐标. 【例3】(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为;
