导数与微分的联系与区别

导数和微分的概念

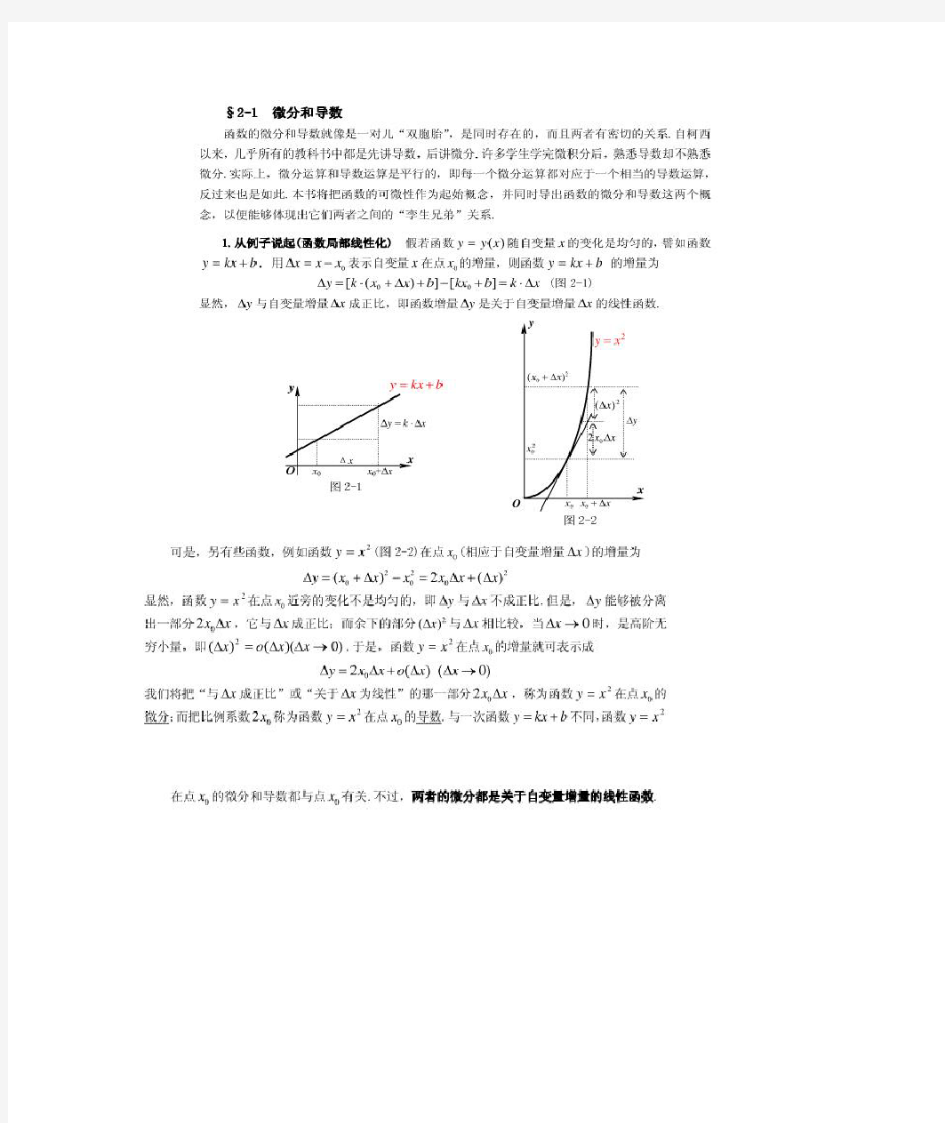
一元函数微分学 §1 导数和微分的概念 基本概念 1. 导数定义 00000)()(lim lim )()(lim 0x x x f x f x y x x f x x f x x x x --=??=?-?+→→?→? 0|)()(00x x dx dy x y x f =='='= 几种极限形式都要掌握 函数在某点可导即上述极限存在，极限存在?左右极限都存在且相等，左极限为左导，右极限为右导， )(lim 00x f x y x --→?'=??， )(lim 00x f x y x ++→?'=?? 导数定义是非常重要的概念，一定要灵活掌握。 2. 导函数)(x f ',dx dy . f (x )在（a , b ）可导, f (x )在[a , b ]可导 3. 可导与连续的关系 可导一定连续，但连续不一定可导（如函数||x y =在x =0点处连续，但是不可导） 4. 导数的几何意义 切线方程：))((000x x x f y y -'=-； 法线方程：)() (1000x x x f y y -'- =- 0)(0≠'x f ， 5. 微分的定义

微分的几何意义 6. 微分与导数的关系 )(x f 在x 处可微?)(x f 在x 处可导，且dx x f dy )('= 同时 dx x f dy x x )(|00'==。 §2 导数与微分的计算 基本概念 1. 基本初等函数的导数、微分公式（书159页，166页） 2. 导数（微分）四则运算公式 )()())()((x g x f x g x f '±'='±， )()()()())()((x g x f x g x f x g x f '+'='， 特别地 )())((x f k x kf '='， ) ()()()()())()((2x g x g x f x g x f x g x f '-'=' 特别地 ) ()())(1(2x f x f x f '-='。 后面两个公式不要记错。 3. 复合函数的求导法则 如何正确运用好复合函数求导法则（必须明确函数的复合过程），并且应到最后一层复合 4．高阶导数（计算同一阶导数）。

最新导数和微分的概念

导数和微分的概念

一元函数微分学 §1 导数和微分的概念 基本概念 1.导数定义 ?Skip Record If...? ?Skip Record If...? 几种极限形式都要掌握 函数在某点可导即上述极限存在，极限存在?Skip Record If...?左右极限都存在且相等，左极限为左导，右极限为右导， ?Skip Record If...?， ?Skip Record If...? 导数定义是非常重要的概念，一定要灵活掌握。 2.导函数?Skip Record If...?,?Skip Record If...?. f(x)在（a, b）可导, f(x)在[a, b]可导 3.可导与连续的关系 可导一定连续，但连续不一定可导（如函数?Skip Record If...?在x=0点处连续，但是不可导） 4.导数的几何意义 切线方程：?Skip Record If...?； 法线方程：?Skip Record If...? ?Skip Record If...?， 5.微分的定义 微分的几何意义 6.微分与导数的关系

?Skip Record If...?在x处可微?Skip Record If...??Skip Record If...?在x处可导，且?Skip Record If...? 同时 ?Skip Record If...?。 §2 导数与微分的计算 基本概念 1.基本初等函数的导数、微分公式（书159页，166页） 2.导数（微分）四则运算公式 ?Skip Record If...?， ?Skip Record If...?， 特别地 ?Skip Record If...?， ?Skip Record If...? 特别地 ?Skip Record If...?。 后面两个公式不要记错。 3.复合函数的求导法则 如何正确运用好复合函数求导法则（必须明确函数的复合过程），并且应到最后一层复合 4．高阶导数（计算同一阶导数）。 §3 中值定理 基本概念

高数第三章一元函数的导数和微分

第三章一元函数的导 数和微分【字体：大中小】【打印】 3.1 导数概念 一、问题的提出 1.切线问题 割线的极限位置——切线位置 如图，如果割线MN绕点M旋转而趋向极限位置MT，直线MT就称为曲线C在点M处的切线. 极限位置即 切线MT的斜率为 2.自由落体运动的瞬时速度问题

二、导数的定义 设函数y=f（x）在点的某个邻域内有定义，当自变量x在处取得增量Δx（点仍在该邻域内）时，相应地函数y取得增量；如果Δy与Δx之比当Δx→0时的极限存在，则称函数y=f（x）在点处可导，并称这个极限为函数 y=f（x）在点处的导数，记为 即 其它形式 关于导数的说明： 在点处的导数是因变量在点处的变化率，它反映了因变量随自变量的变化而变化的快慢程度。 如果函数y=f（x）在开区间I内的每点处都可导，就称函数f（x）在开区间I内可导。 对于任一，都对应着f（x）的一个确定的导数值，这个函数叫做原来函数f（x）

的导函数，记作 注意： 2.导函数（瞬时变化率）是函数平均变化率的逼近函数. 导数定义例题： 例1、115页8 设函数f（x）在点x=a可导，求： （1） 【答疑编号11030101：针对该题提问】 （2） 【答疑编号11030102：针对该题提问】

三、单侧导数 1.左导数： 2.右导数： 函数f（x）在点处可导左导数和右导数都存在且相等. 例2、讨论函数f（x）=|x|在x=0处的可导性。 【答疑编号11030103：针对该题提问】 解

闭区间上可导的定义：如果f（x）在开区间（a，b）内可导，且及都存在，就说f（x）在闭区间[a，b]上可导. 由定义求导数 步骤： 例3、求函数f（x）=C（C为常数）的导数。 【答疑编号11030104：针对该题提问】 解 例4、设函数 【答疑编号11030105：针对该题提问】 解

导数与微分练习题答案

高等数学练习题 第二章 导数与微分 第一节 导数概念 一．填空题 1.若)(0x f '存在，则x x f x x f x ?-?-→?) ()(lim 000 = )(0x f '- 2. 若)(0x f '存在，h h x f h x f h ) ()(lim 000 --+→= )(20x f ' . 000 (3)() lim x f x x f x x ?→+?-?=03()f x '. 3.设20-=')(x f , 则=--→)()2(lim )000 x f x x f x x 4 1 4.已知物体的运动规律为2 t t s +=(米)，则物体在2=t 秒时的瞬时速度为5（米/秒） 5.曲线x y cos =上点（ 3 π ，21）处的切线方程为03 123=- -+π y x ，法线方程为 03 22332=-+ -π y x 6.用箭头?或?表示在一点处函数极限存在、连续、可导、可微之间的关系， 可微 ? 可导 <≠ ? | 连续 <≠ ? 极限存在。 二、选择题 1．设0)0(=f ,且)0(f '存在，则x x f x ) (lim 0→= [ B ] （A ）)(x f ' ( B) )0(f ' (C) )0(f (D) 2 1 )0(f 2. 设)(x f 在x 处可导，a ,b 为常数，则x x b x f x a x f x ??--?+→?) ()(lim 0 = [ B ] （A ）)(x f ' ( B) )()(x f b a '+ (C) )()(x f b a '- (D) 2 b a +)(x f ' 3. 函数在点0x 处连续是在该点0x 处可导的条件 [ B ] （A ）充分但不是必要 （B ）必要但不是充分 （C ）充分必要 （D ）即非充分也非必要 4．设曲线22 -+=x x y 在点M 处的切线斜率为3，则点M 的坐标为 [ B ] （A ）(0,1) ( B) (1, 0) (C) ( 0,0) (D) (1,1)

导数与微分测试题及答案(一)

导数与微分测试题（一） 一、选择题（每小题4分，共20分） 1、 设函数10 ()10 2 x x f x x ?≠??=??=?? 在0x =处（ ） A 、不连续； B 、连续但不可导； C 、二阶可导； D 、仅一阶可导； 2、若抛物线2y ax =与曲线ln y x =相切，则a 等于（ ） A 、1； B 、 12 ； C 、 12e ； D 、2e ； 3、设函数()ln 2f x x x =在0x 处可导，且0()2f x '=，则0()f x 等于（ ） A 、1； B 、 2 e ； C 、 2e ； D 、e ； 4、设函数()f x 在点x a =处可导，则0 ()() lim x f a x f a x x →+--等于（ ） A 、0； B 、()f a '； C 、2()f a '； D 、(2)f a '； 5、设函数()f x 可微，则当0x ?→时，y dy ?-与x ?相比是（ ） A 、等价无穷小； B 、同阶非等价无穷小； C 、低阶无穷小； D 、高阶无穷小； 二、填空题（每小题4分，共20分） 1、设函数()f x x x =，则(0)f '=______； 2、 设函数()x f x xe =，则(0)f ''=______； 3、 设函数()f x 在0x 处可导，且0()f x =0，0()f x '=1，则 01lim ()n nf x n →∞ + =______； 4、 曲线2 28y x x =-+上点______处的切线平行于x 轴，点______处的 切线与x 轴正向的交角为 4 π 。

5、 d ______ = x e dx - 三、解答题 1、（7分）设函数()()() , ()f x x a x x ??=-在x a =处连续， 求()f a '； 2、（7分）设函数()a a x a x a f x x a a =++，求()f x '； 3、（8分）求曲线 sin cos 2x t y t =?? =? 在 6 t π = 处的切线方程和法线方程； 4、（7分）求由方程 1sin 02 x y y -+=所确定的隐函数y 的二阶导数 2 2 d y dx 5、（7分）设函数1212()()()n a a a n y x a x a x a =--- ，求 y ' 6、（10分）设函数2 12()12 x x f x ax b x ?≤?? =? ?+> ?? ，适当选择,a b 的值，使 得()f x 在12 x = 处可导 7（7分）若2 2 ()()y f x xf y x +=，其中 ()f x 为可微函数，求dy 8、（7分）设函数()f x 在[,]a b 上连续，且满足 ()()0,()()0f a f b f a f b +-''==?>，证明：()f x 在(,)a b 内至少存在一点c ，使得 ()0f c = 导数与微分测试题及答案（一） 一、1－5 CCBCD 二、1. 0； 2. 2； 3. 1； 4.（1，7）、329(, )24 ； 5. x e --； 三、1. 解：()() ()() ()lim lim ()x a x a f x f a x a x f a a x a x a ??→→--'===--；

03第三章-导数与微分

第三章 导数与微分 一、本章学习要求与内容提要 （一）学习要求 1. 理解导数和微分的概念及其几何意义，会用导数（变化率）描述一些简单的实际问题. 2.熟练掌握导数和微分的四则运算法则和基本初等函数的求导公式. 3.熟练掌握复合函数、隐函数以及由参数方程所确定的函数的一阶导数的求法. 4.了解高阶导数的概念，熟练掌握初等函数的二阶导数的求法. 5.了解可导、可微、连续之间的关系. 重点 导数的概念及其几何意义，计算导数的方法，初等函数的二阶导数的求法. 难点 求复合函数和隐函数的导数的方法. （二） 内容提要 1.导数的概念 ⑴导数 设函数)(x f y =在点0 x 的某一邻域内有定义，当自变量x 在点0 x 处有增量)0(≠??x x ，x x ?+0 仍在该邻域内时，相应地，函数有增量)()(0 x f x x f y -?+=?，若极限 000 0()()lim lim x x f x x f x y x x ?→?→+?-?=?? 存在，则称)(x f 在点0 x 处可导，并称此极限值为)(x f 在点0 x 处的导数，记为)(0 x f '，也可记为0 00 0d d d d , ,)(x x x f x x x y x x y x y ===' '或，即 x x f x x f x y x f x x ?-?+=??='→?→?)()(lim lim )(00000. 若极限不存在，则称)(x f y =在点0 x 处不可导. 若固定0 x ，令x x x =?+0 ，则当0→?x 时，有0x x →，所以函数)(x f 在 点0 x 处的导数)(0 x f '也可表示为 00 ) ()(lim )(x x x f x f x f x --='→.

第二章 导数与微分(测试题)

第二章 导数与微分 单元测试题 考试时间：120分钟 满分：100分 试卷代码：M1-2b 一、选择题(每小题2分，共40分) 1．两曲线21y y ax b x = =+，在点1(22 ，处相切，则（ ） A．13164a b =-=， B．11164 a b ==， C．912a b =-=， D．712a b ==-， 2．设(0)0f =，则()f x 在0x =可导的充要条件为（ ） A．201lim (1cos )h f h h →-存在 B．01lim (1)h h f e h →-存在 C．201lim (sin )h f h h h →-存在 D．[]01lim (2)()h f h f h h →-存在 3．设函数()f x 在区间()δδ-，内有定义，若当()x δδ∈-，时恒有2()f x x ≤，则0x =必是()f x 的（ ） A．间断点 B．连续而不可导的点 C．可导的点，且(0)0f '= D．可导的点，且(0)0f '≠ 4．设函数()y f x =在0x 点处可导，x y ，分别为自变量和函数的增量，dy 为其微分且0()0f x '≠，则0lim x dy y y →-= （ ） A．-1 B．1 C．0 D．∞ 5．设()f x 具有任意阶导数，且[]2 ()()f x f x '=，则()()n f x =（ ） A．[]1()n n f x + B．[]1!()n n f x + C．[]1(1)()n n f x ++ D．[]1(1)!()n n f x ++ 6．已知函数 0() 0x x f x a b x x x ≤??=?>?? +cos 在0x =处可导，则（ ） A．22a b =-=， B．22a b ==-， C．11a b =-=， D．11a b ==-， 7．设函数32()3f x x x x =+，则使()(0)n f 不存在的最小正整数n 必为（ ） A．1 B．2 C．3 D．4 8．若()f x 是奇函数且(0)f '存在，则0x =是函数()()f x F x x =的（ ）

第三章导数与微分习题解答

P61 习题3-1 1、根据定义求导数： (1)cos y x = 00000cos()cos lim 2sin sin 22lim sin()sin 22lim 2 sin 2lim sin()lim 22 sin x x x x x x x x y x x x x x x x x x x x x x x x x ?→?→?→?→?→+?-'=?+?++?--=???+=-???=-+?=- 12 (2)y x = 112 2 012()lim lim lim 12x x x x x x y x x ?→?→?→-+?-'=?==== (3)y = 033 223 2 2 2(lim lim lim lim x x x x x x y x ?→?→?→?→+?'=?==== =(4)x y a = 001lim lim x x x x x x x a a a y a x x +???→?→--'==?? 设t x =?，则 01 lim t x t a y a t →-'= 再设t s a =，则log a t s =，于是 11 1 1 110 1 1lim log 1lim log 1 lim log [1(1)] 1log ln x s a x s s a x s s a x a x s y a s a s a s a e a a →→--→--'===+-== 2、

0000000()()(1)lim [(()]() lim () x x f x x f x x f x x f x x f x ?→-?→-?-?+-?-=--?'=- 00000000000000000000000()()(2)lim ()()()()lim ()()()()lim lim ()()()()lim lim ()[()]2() x x x x x x f x x f x x x f x x f x f x f x x x f x x f x f x f x x x x f x x f x f x x f x x x f x f x f x ?→?→?→?→?→?→+?--??+?-+--?=?+?---?=+??+?--?-=-??''=--'= 000()(3)lim ()lim (0)(0)lim (0) x x x f x x f x x f x f x f →?→?→?=?+?-=?'= 00001001 (4)lim [()()]1 ()() lim 1() n n n f x f x n f x f x n n f x →∞→+-+-='= 3、证： ()f x 为偶函数且(0)0f =，则 00000(0)(0)(0)lim ()(0) lim ()(0) lim ()(0) lim ()(0) lim (0)x x x x x f x f f x f x f x f x f x f x f x f x f x f - - - - + -?→?→?→?→-?→++?-'=??-=?-?-=?-?-=--?-?-=--?'=- 又()f x 在0x =处可导，则 (0)(0)f f -+''= 即(0)(0)f f ++''=- 所以(0)0f +'= 故(0)0f '=。 4、证： （1）设()f x 为可导的奇函数，则： 0000()()()lim ()()lim ()() lim [()]() lim ()x x x x f x x f x f x x f x x f x x f x x f x x f x x f x x f x ?→?→?→-?→-+?--'-=?--?+=?-?-=-?+-?-=-?'= 所以()f x '为偶函数。 （2）设()f x 为可导的偶函数，则：

偏导数与全导数偏微分与全微分的关系

偏导数与全导数偏微分与全微分的关系 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】

1。偏导数代数意义偏导数是对一个变量求导,另一个变量当做数对x求偏导的话y就看作一个数，描述的是x方向上的变化率对y求偏导的话x就看作一个数，描述的是y方向上的变化率 几何意义对x求偏导是曲面z=f(x,y)在x方向上的切线对y求偏导是曲面z=f(x,y)在x方向上的切线 这里在补充点。就是因为偏导数只能描述x方向或y方向上的变化情况，但是我们要了解各个方向上的情况，所以后面有方向导数的概念。 2。微分偏增量：x增加时f(x,y)增量或y增加时f(x,y) 偏微分：在d e t a x趋进于0时偏增量的线性主要部分d e t a z=f x（x,y）d e t a x+o(d e t a x) 右边等式第一项就是线性主要部分，就叫做在（x，y）点对x的偏微分这个等式也给出了求偏微分的方法，就是用求x的偏导数求偏微分

全增量：x,y都增加时f(x,y)的增量全微分：根号(detax方+detay方）趋于0时，全增量的线性主要部分同样也有求全微分公式，也建立了全微分和偏导数的关系d z=A d x+B d y其中A就是对x求偏导，B就是对y求偏导 希望楼主注意的是导数和微分是两个概念，他们之间的关系就是上面所说的公式。概念上先有导数，再有微分，然后有了导数和微分的关系公式，公式同时也指明了求微分的方法。 3.全导数全导数是在复合函数中的概念，和上面的概念不是一个系统，要分开。u=a(t),v=b(t) z=f[a(t),b(t)] dz/dt 就是全导数，这是复合函数求导中的一种情况，只有这时才有全导数的概念。 d z/d t=(偏z/偏u)(d u/d t)+(偏z/偏v)(d v/d t) 建议楼主在复合函数求导这里好好看看书，这里分为3种情况。1.中间变量一元就是上面的情况，才有全导数的概念。2.中间变量有多元，只能求偏导 3.中间变两有一元也有多元，还是求偏导。 对于你的题能求对x的偏导数，对y的偏导数，z的全微分，不能求全导数

第三章 导数与微分 习题及答案

第三章 导数与微分 同步练习 一、填空 1、若[]1cos 1)0()(lim =--→x f x f x x ，则)0(f '= 。 2、设)100()3)(2)(1()(----=x x x x x x f ，则)0(f '= 。 3、若)(x e f y -=，且x x x f ln )(='，则 1 =x dx dy = 。 4、若)()(x f x f =-，且3)1(=-'f ，则)1(f '= 。 5、设某商品的需求函数是Q=10-0.2p ，则当价格p=10时，降价10%，需求量将 。 6、设某商品的需求函数为：Q=100-2p ，则当Q=50时，其边际收益为 。 7、已知x x y ln =，则)10(y = 。 8、已知2arcsin )(),232 3( x x f x x f y ='+-=，则：0 =x dx dy = 。 9、设1 111ln 2 2++-+=x x y ，则y '= 。 10、设方程y y x =确定y 是x 的函数，则dy = 。 11、已知()x ke x f ='，其中k 为常数，求()x f 的反函数的二阶导数=22dy x d 。 二、选择 1、设f 可微，则=---→1 ) 1()2(lim 1 x f x f x （ ） A 、)1(-'-x f B 、)1(-'f C 、)1(f '- D 、)2(f ' 2、若2)(0-='x f ，则=--→) ()2(lim 000 x f x x f x x （ ） A 、 41 B 、4 1 - C 、1 D 、-1 3、设?? ???=≠=0001arctan )(x x x x x f ，则)(x f 在0=x 处（ ） A 、不连续 B 、极限不存在 Ｃ、连续且可导 Ｄ、连续但不可导 ４、下列函数在[]1,1-上可微的有（ ） Ａ、x x y sin 3 2+= Ｂ、x x y sin =

经济数学(导数与微分习题与答案)

第三章 函数的导数与微分 习题 3－1 1. 根据定义求下列函数的导数: (1) x y 1 = (2)x y cos = (3)b ax y +=(a ,b 为常数) (4)x y = 解(1)因为 00()()'lim lim x x y f x x f x y x x ?→?→?+?-==?? =x x x x x ?-?+→?1 1lim 0=01lim ()x x x x ?→-+?=21 x - 所以 21 y x '=- . (2) 因为00cos()cos 'lim lim x x y x x x y x x ?→?→?+?-==?? 02sin()sin 22 lim sin x x x x x x ?→??-+==-? 所以sin y x '=- (3) 因为 00[()][]'lim lim x x y a x x b ax b y x x ?→?→?+?+-+==?? =x x a x ??→?0lim =a 所以y a '= (4) 因为 00'lim lim x x y y x x ?→?→?-==?? = )(lim 0x x x x x x +?+??→? lim x ?→== 所以 y '= . 2. 下列各题中假定)(0' x f 存在, 按照导数的定义观察下列极限, 指出A 表示什么? (1) A x x f x x f x =?-?-→?)()(lim 000 (2) A x x f x =→)(lim 0(其中0)0(=f 且)0(' f )存在) (3) A x f tx f x =-→)0()(lim 0(其中)0(' f 存在)

偏导数与全导数-偏微分与全微分的关联

1。偏导数 代数意义 偏导数是对一个变量求导,另一个变量当做数 对x求偏导的话y就看作一个数，描述的是x方向上的变化率 对y求偏导的话x就看作一个数，描述的是y方向上的变化率 几何意义 对x求偏导是曲面z=f(x,y)在x方向上的切线 对y求偏导是曲面z=f(x,y)在x方向上的切线 这里在补充点。就是因为偏导数只能描述x方向或y方向上的变化情况，但是我们要了解各个方向上的情况，所以后面有方向导数的概念。 2。微分 偏增量：x增加时f(x,y)增量或y增加时f(x,y) 偏微分：在detax趋进于0时偏增量的线性主要部分 detaz=fx（x,y）detax+o(detax) 右边等式第一项就是线性主要部分，就叫做在（x，y）点对x的偏微分 这个等式也给出了求偏微分的方法，就是用求x的偏导数求偏微分 全增量：x,y都增加时f(x,y)的增量 全微分：根号(detax方+detay方）趋于0时，全增量的线性主要部分

同样也有求全微分公式，也建立了全微分和偏导数的关系 dz=Adx+Bdy 其中A就是对x求偏导，B就是对y求偏导 希望楼主注意的是导数和微分是两个概念，他们之间的关系就是上面所说的公式。概念上先有导数，再有微分，然后有了导数和微分的关系公式，公式同时也指明了求微分的方法。 3.全导数 全导数是在复合函数中的概念，和上面的概念不是一个系统，要分开。 u=a(t),v=b(t) z=f[a(t),b(t)] dz/dt 就是全导数，这是复合函数求导中的一种情况，只有这时才有全导数的概念。 dz/dt=(偏z/偏u)(du/dt)+(偏z/偏v)(dv/dt) 建议楼主在复合函数求导这里好好看看书，这里分为3种情况。1.中间变量一元就是上面的情况，才有全导数的概念。2.中间变量有多元，只能求偏导 3.中间变两有一元也有多元，还是求偏导。 对于你的题能求对x的偏导数，对y的偏导数，z的全微分，不能求全导数 如果z=f(x^2,2^x) 只有这种情况下dz/dx才是全导数！

导数与微分习题及答案

第二章 导数与微分 (A) 1．设函数()x f y =，当自变量x 由0x 改变到x x ?+0时，相应函数的改变量=?y ( ) A ．()x x f ?+0 B ．()x x f ?+0 C ．()()00x f x x f -?+ D ．()x x f ?0 2．设()x f 在0x 处可，则()()=?-?-→?x x f x x f x 000lim ( ) A ．()0x f '- B ．()0x f -' C ．()0x f ' D ．()02x f ' 3．函数()x f 在点0x 连续，是()x f 在点0x 可导的 ( ) A ．必要不充分条件 B ．充分不必要条件 C ．充分必要条件 D ．既不充分也不必要条件 4．设函数()u f y =是可导的，且2x u =，则=dx dy ( ) A ．()2x f ' B ．()2x f x ' C ．()22x f x ' D ．()22x f x 5．若函数()x f 在点a 连续，则()x f 在点a ( ) A ．左导数存在； B ．右导数存在； C ．左右导数都存在 D ．有定义 6．()2-=x x f 在点2=x 处的导数是( ) A ．1 B ．0 C ．-1 D ．不存在 7．曲线545223-+-=x x x y 在点()1,2-处切线斜率等于( ) A ．8 B ．12 C ．-6 D ．6 8．设()x f e y =且()x f 二阶可导，则=''y ( ) A ．()x f e B ．()()x f e x f '' C ．()()()[]x f x f e x f ''' D ．()()[](){} x f x f e x f ''+'2 9．若()???≥+<=0 ,2sin 0,x x b x e x f ax 在0=x 处可导，则a ，b 的值应为( ) A ．2=a ，1=b B ． 1=a ，2=b C ．2-=a ，1=b D ．2=a ，1-=b

导数与微分的关系

导数与微分的关系 宁小青 我们知道一个函数在某点可导和可微是等价的，大部分高等数学、经济数学和数学分析课本中都是先引进导数的概念，再引进微分的概念，到底导数和微分这两个概念，哪个概念产生在前、哪个概念产生在后呢？ 一、微分概念的导出背景 当一个函数的自变量有微小的改娈时，它的因变量一般说来也会有一个相应的改变。微分的原始思想在于去寻找一种方法，当因变量的改变也是很微小的时候，能够简便而又比较精确地估计出这个改变量。 我们来看一个简单的例子： 维持物体围绕地球作永不着地（理论上）的飞行所需要的最低速度称为第一宇宙速度。在中学里，利用计算向凡加速度的办法已经求出这种速度约为7.9千米/秒，现在我们改用另一种思路去推导它。 设卫星当前时刻在地球表面附近的A点沿着水平方向飞行，假如没有外力影响的话，那么它在一秒种后本应到达B点，但事实上它要受到地球的引力，因而实际到达的并非是B 点，而是C点，BC=4.9米是自由落体在重力加速度的作用下，第一秒中所走过的距离。 容易看出，若C点与地心O的距离与A事点到O的距离是相等的，那么由运动的独立性原理，就可以推断出卫星在沿地球的一个同心圆轨道运行，也就是作环绕地球的飞行了。因此，卫星应具有最小每秒飞行速度恰好在线段AB的长度。△OAB是直角三角形，OA和OC可近似的取为地球的平均半径6371千米，也就是6371000米，于是由勾股定理 显然就这样按上式去计算是不可取的——这将导致两个量级的数在直接相减，工作量大不说，在字长较短的计算机上，还可能产生较大的误差。 利用乘法公式 可将上式改为 由于，因此这一项与这一项想比可以忽略不计，于是可以把计算简化为 由此计算出千米。 这就是说，卫星的速度至少要达到每秒7.9千米才能维持其围绕地球的飞行，此即所要求的第一宇宙速度。 上面所计算的，实际上就是函数在处，自变量出现了一个微小的改变量之后，函数值的相应改变量4.9。然而在计算过程中，我们并没有完全精确地去算

导数与微分导数概念

第二章 导数与微分 第一节 导数概念 1.x x x y = ，求y ' 2．求函数y =2tan x +sec x -1的导数y ' 3. x x y 1010 +=，求y ' 4. 求曲线y =cos x 上点)2 1 ,3(π处的切线方程和法线方程式. 5.3ln ln +=x e y ，求y ' 6.已知? ??<-≥=0 0 )(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在？ 7.设????? =≠=0 ,00 ,1sin )(x x x x x f ，用定义证明)(x f 在点0=x 处连续，但不可导。

8. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 . 9.讨论函数y =|sin x |在x =0处的连续性与可导性: 10.设函数? ??>+≤=1 1 )(2x b ax x x x f ，为了使函数f (x )在x =1处连续且可导, a , b 应取什么值？ 第二节 函数的求导法则 1.设()22arcsin x y =，求y ' 2．求函数y =sin x ?cos x 的导数y ' 3．求函数y =x 2ln x 的导数y '

4．求函数x x y ln =的导数y ' 5．求函数3ln 2+=x e y x 的导数y ' 6. )(cos )(sin 2 2x f x f y +=，求y ' 7. n b ax f y )]([+=，求y ' 8. ) ()(x f x e e f y =，求y ' 9. x x x y arcsin 12 +-=，求y ' 10．求函数y =x 2ln x cos x 的导数y ' 第三节 高阶导数 1. x x x y ln 1 arctan +=，求y ''

高等数学导数与微分练习题

作业习题 1、求下列函数的导数。 （1）223)1(-=x x y ； （2）x x y sin = ； （3）bx e y ax sin =； （4）)ln(22a x x y ++=；（5）11arctan -+=x x y ；（6）x x x y )1(+=。 2、求下列隐函数的导数。 （1）0)cos(sin =+-y x x y ；（2）已知,e xy e y =+求)0(y ''。 3、求参数方程???-=-=) cos 1()sin (t a y t t a x )0(>a 所确定函数的一阶导数dx dy 与二阶导数 2 2dx y d 。 4、求下列函数的高阶导数。 （1）,αx y =求)(n y ； （2）,2sin 2x x y =求)50(y 。 5、求下列函数的微分。 （1）)0(,>=x x y x ； （2）2 1arcsin x x y -= 。 6、求双曲线122 22=-b y a x ，在点)3,2(b a 处的切线方程与法线方程。 7、用定义求)0(f '，其中?????=, 0,1sin )(2 x x x f .0, 0=≠x x 并讨论导函数的连续性。 作业习题参考答案： 1、（1）解：])1[()1()(])1([23223223'-+-'='-='x x x x x x y ]))(1(2[)1(3223222'-+-=x x x x x x x x x x 2)1(2)1(323222?-+-= )37)(1(222--=x x x 。 （2）解：2sin cos )sin ( x x x x x x y -='='。 （3）解：bx be bx ae bx e y ax ax ax cos sin )sin (+='=' )cos sin (bx b bx a e ax +=。

导数与微分练习题答案

高等数学练习题 第二章 导数与微分 第一节 导数概念 一．填空题 1.若)(0x f '存在，则x x f x x f x ?-?-→?) ()(lim 000 = )(0x f '- 2. 若)(0x f '存在，h h x f h x f h ) ()(lim 000 --+→= )(20x f ' . 000 (3)() lim x f x x f x x ?→+?-?=03()f x '. 3.设20-=')(x f , 则=--→)()2(lim )000 x f x x f x x 4 1 4.已知物体的运动规律为2 t t s +=(米)，则物体在2=t 秒时的瞬时速度为5（米/秒） 5.曲线x y cos =上点（ 3 π ，21）处的切线方程为03 123=- -+π y x ，法线方程为 03 22332=-+ -π y x 6.用箭头?或?表示在一点处函数极限存在、连续、可导、可微之间的关系， ； 可微 ? 可导 <≠ ? | 连续 <≠ ? 极限存在。 二、选择题 1．设0)0(=f ,且)0(f '存在，则x x f x ) (lim 0→= [ B ] （A ）)(x f ' ( B) )0(f ' (C) )0(f (D) 2 1 )0(f 2. 设)(x f 在x 处可导，a ,b 为常数，则x x b x f x a x f x ??--?+→?) ()(lim 0 = [ B ] （A ）)(x f ' ( B) )()(x f b a '+ (C) )()(x f b a '- (D) 2 b a +)(x f ' 3. 函数在点 x 处连续是在该点 x 处可导的条件 [ B ] （A ）充分但不是必要 （B ）必要但不是充分 （C ）充分必要 （D ）即非充分也非必要 4．设曲线22 -+=x x y 在点M 处的切线斜率为3，则点M 的坐标为 [ B ]

高等数学第三章导数与微分

第三章导数与微分 一、导数概念与定义 A 、导数的概念 a 、设函数y=f （x ）在点0x 处的某临域内有定义，当自变量x 在0x 处取得变量△x （△x ≠0）时，函数取得 相应增量。即△y=f （0x +△x ）-f （0x ） 若△y 与△x 之比当△x →0时极限存在，即000()()lim x f x x f x x ?→+?-?存在，，则称函数在点0x 处可导，0x 为()y f x =的可导点，并称此极限为函数在点0x 处的导数。 法线的斜率为1k ，切线的斜率为k b 、若0 000()()()lim x x f x f x f x x x →-'=→不存在，则称()f x 在0x 处不可导或不存在导数，0x 为()f x 的不可导点。 ※特别是当上述极限为无穷大时，此时导数不存在，或称()f x 在点0x 处的导数无穷大。 导数()f x '也可记为0|x x dy dx =或0()|f x x x x d d = c 、函数的左导数与右导数 0000()()()lim x f x f x f x x x --→-'=→ 0000 ()()()lim x f x f x f x x x ++→-'=→ ※分段函数的分段点处考虑左导右导，其余正常求导时直接求()f x ' B 、导数的几何意义 曲线在点00(,())x f x 处的切线方程为000()()y y f x x x '-=- 曲线在点00(,())x f x 处的发现方程为0001()()y y x x f x --= -' C 、函数的可导性与连续性的关系 函数()y f x =在0x 处可导，则在0x 处连续；但函数()y f x =在0x 处连续，在点0x 不一定可导。 二、求导法则 A 、 代数和的求导法则，积的导数、商的导数 ① ()u v u v '''+=+ ② ()u v u v v u '''?=+ ③ ()cu cu ''= ④ ()au bv au bv '''±=± ⑤ ()u v w s t u vwst uv wst uvw st uvws t uvwst ''''''????=++++ 即n 个因子乘积的导数一定为n 项，且每项均为n 个因子的乘积，第i 项的第i 个因子求导，其余不变 ⑥ 2()u u v v u v v ''-'= B 、 反函数的导数

3第三章 微分中值定理与导数的应用习题解答

第三章 微分中值定理与导数的应用答案 §3.1 微分中值定理 1． 填空题 （１）函数x x f arctan )(=在]1 ,0[上使拉格朗日中值定理结论成立的ξ是 π π -4． （２）设)5)(3)(2)(1()(----=x x x x x f ，则0)(='x f 有 3 个实根，分别位于区间)5,3(),3,2(),2,1(中． 2． 选择题 （１）罗尔定理中的三个条件:)(x f 在],[b a 上连续，在),(b a 内可导，且)()(b f a f =，是)(x f 在),(b a 内至少存在一点ξ，使0)(='ξf 成立的（ B ）． A ． 必要条件 B ．充分条件 C ． 充要条件 D ． 既非充分也非必要条件 （２）下列函数在]1 ,1[-上满足罗尔定理条件的是（ C ）． A . x e x f =)( B. ||)(x x f = C. 2 1)(x x f -= D. ????? =≠=0 ,00 ,1sin )(x x x x x f （３）若)(x f 在),(b a 内可导，且21x x 、是),(b a 内任意两点，则至少存在一点ξ，使下式成 立（ B ）． A ． ),() ()()()(2112b a f x x x f x f ∈'-=-ξξ B ． ξξ)()()()(2121f x x x f x f '-=-在12,x x 之间 C ． 211221)()()()(x x f x x x f x f <<'-=-ξξ D ． 211212)()()()(x x f x x x f x f <<'-=-ξξ 3．证明恒等式：)(2 cot arctan ∞<<-∞= +x x arc x π ． 证明： 令x arc x x f cot arctan )(+=，则011 11)(2 2=+-+='x x x f ，所以)(x f 为一常数． 设c x f =)(，又因为(1)2 f π = ， 故 )(2 c o t a r c t a n ∞<<-∞=+x x arc x π ． 4．若函数)(x f 在),(b a 内具有二阶导数，且)()()(321x f x f x f ==，其中12a x x << 3x b <<，证明:在),(31x x 内至少有一点ξ，使得0)(=''ξf ． 证明：由于)(x f 在],[21x x 上连续,在),(21x x 可导,且)()(21x f x f =，根据罗尔定理知，存在),(211x x ∈ξ， 使0)(1='ξf ． 同理存在),(322x x ∈ξ，使0)(2='ξf ． 又)(x f '在],[21ξξ上 符合罗尔定理的条件，故有),(31x x ∈ξ，使得0)(=''ξf ．

十偏导数与全微分(学生用)

第十四章 偏导数与全微分 §1. 偏导数与全微分的概念 1．求下列函数的偏导数： (1) 2 2 2 ln()u x x y =+； (2) ()cos()u x y xy =+； (3) arctan x u y =； (4) sin()xy u xye =. 2．设22 22 221sin , 0,(,)0, 0.y x y x y f x y x y ?+≠?+=??+=? ，考察函数在(0,0)点的偏导数. 3 ．证明函数u =(0,0)点连续但偏导数不存在. 4．求下列函数的全微分： (1) u = (2) yz x u xe e y -=++.

5．求下列函数在给定点的全微分： (1) u =在点(1,1,1)； (2) (u x y =+-0，1）. 6．证明函数22222 22, 0,(,) 0, 0.x y x y f x y x y x y ?+≠?=+??+=? 在(0,0)点连续且偏导数存在，但在此点不可微。 7 ．证明：函数22 220(,)0, 0x y f x y x y +≠=+=?在点(0, 0)处偏导数存在，但不可微. 8．设,x y 很小，利用全微分推出下列式(1)(1)m n x y ++的近似公式：

9．求下列函数指定阶的偏导数： (1) 3 3 sin sin u x y y x =+,求633u x y ???； (2) ln()u ax by =+,求m n m n u x y +???. §2. 求复合函数偏导数的链式法则 1．求下列函数指定的偏导数： （1）．设(,,),x y z Φ=Φ ,,,x u v y u v z uv =+=-=求, u v ?Φ?Φ ??. （2） 设),,22(xyz z y x f z --=求x z ?? 2. 求下列函数指定的偏导数（假定所有二阶偏导数都连续） (1) 2 2 (,)u f xy x y =，22u x ?? ； (2) (,)x y u f y z =,2u x y ???； (3) 2 2 2 ()u f x y z =++,22u y ??； (4) (,,)x u f x y xy y =+,2u y x ???.