几何五大模型之二：鸟头定理(共角定理)模型

<2>

几何五大模型之二：鸟头定理（共角定理）模型

鸟头定理（共角 定理）模型’

两个三舀葩中有一个角相同或互补，这两个三角形叫做共角三角形。 共角三角形的面和出等于对应角（相同角或互补角）两夹边的乘积之比。

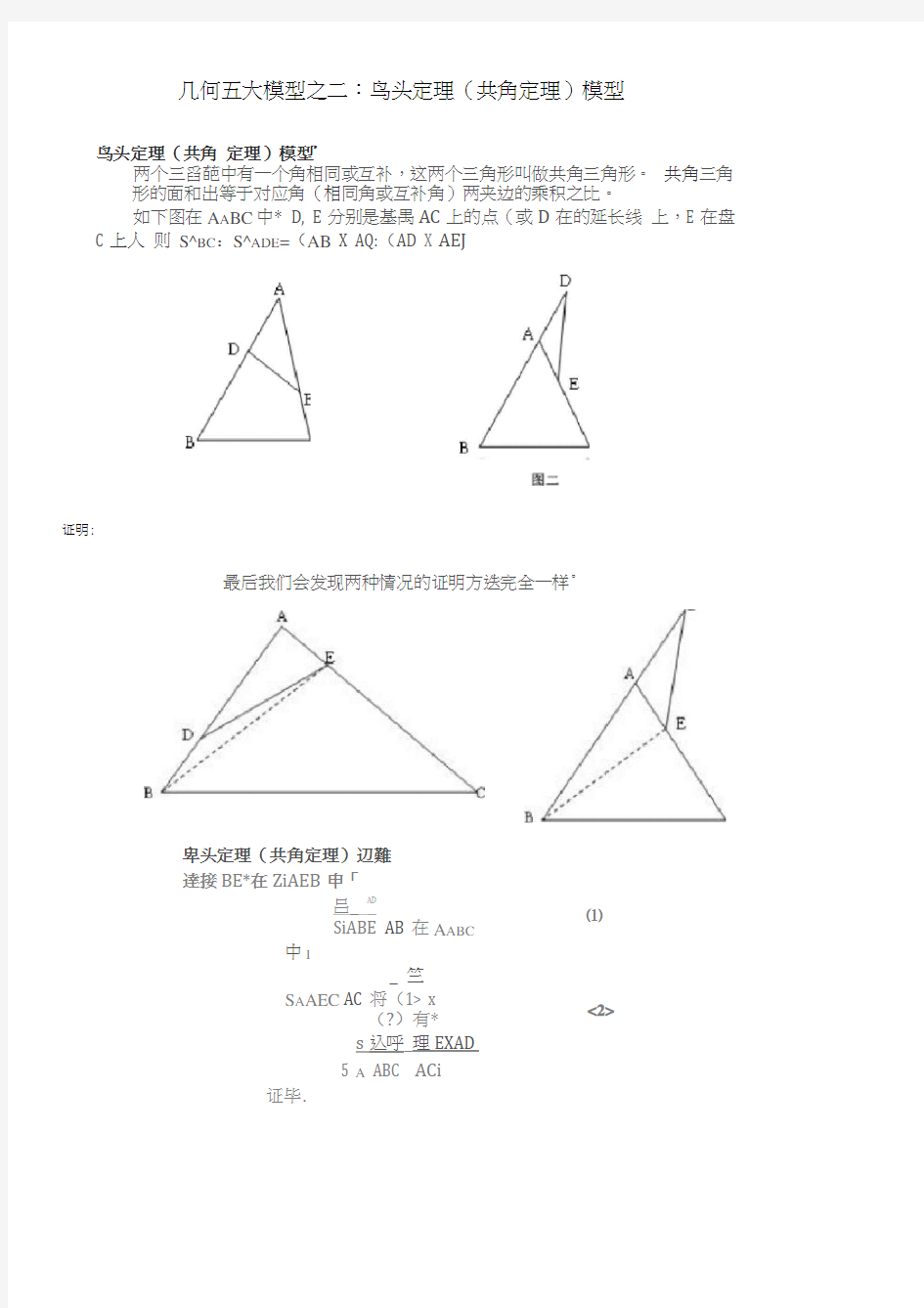
如下图在A A BC 中* D, E 分别是基禺AC 上的点（或D 在的延长线 上，E 在盘C 上人 则 S^BC ：S^ADE =（AB X AQ:（AD X AEJ

证明:

最后我们会发现两种情况的证明方迭完全一样°

卑头定理（共角定理）辺難 逹接BE*在ZiAEB 申「

吕_ AD

SiABE AB 在A ABC

中I

_ 竺

S A AEC AC 将（1> x

（?）有*

s 込呼_理EXAD

5 A ABC ACi

证毕.

⑴

例题1:

如上图，在△ABC 中，D,卫分别是AE AC 卜的点，賞中：ECEAE, AD=2DB, S MEC =1，求△ ADE 的面积?

题_ 解法

利用鸟头定理有：严匹

S^ABC

所 fA SiADE~ 7

AE AD

12 1

__ x ___ = _ V _ ——_ AC X AB 4 X 3 6

本題也可以不用鸟头定理，而用等积变换。 连接BE 在AAEF 中，

S AAED ' S AAEB =AD : AB=2:3 S AAED ^CJ^S ZIAEF 在△ABC 中,

S AAEB ： S AABC =AE: AC=1:4 E △血 EB =（1/4）￡_ABU

由（“（2）式可得

S ^D=

；x|xS_kB c=;

题_

解法二

;

AEXAD ACxAB

诵过观察题一的解袪二我们可以找到一个证明如模型图一中鸟头定理的方

例题2:

如上图「在A ABC 中，E 是AC 上的点，D 县BA 証萇线卜的一占? EC=2AE, AB=2AD, S_AEC =1 ,求 A ADE

的面憩

连接BE 在中，

SUDE _ 空

S 4iABE AS 1SAA&C

中，

SgEE ； _ AE S ￡I AB 匚 AC 将(1)

X (2)有'

S 企ADE ； ” AEX

血D S ^AEC ACXAB 证毕。

Cl)

(2>

题二

解法

利用鸟头定理有:瓷^寫=挣黔存

所以S AADE =7

&

题二解法

二.

本题依然可以不用鸟头定理，而用等积变换。

连接BE,在z\BDE中，

S MED ； S 4 AEB =AD ； AB=1 ； 2

S^AED=(l/2)S a AEB (1)

在△ABC中，

S AAEB： S A ABC=肚:AC=1：3

SaAEB-(l?3 厶ABC (2) 由(1), (2)式可得

S UED兮X^XSwc 气^

同样的，通过观察题二的解法二我们可以找到一个证明如模型图二中鸟头定 理的方法。 D

连接BE,在ZkAEB 中，

S AADE _ AP S AA BE AB 在△ABC

中，

_ AE S AABC AC 将(1)

X (2)有：

S AADE _ AEXAD S A ABC ACXAB

证毕。

(1)

(2)