初中数学勾股定理测试试题及解析

一、选择题

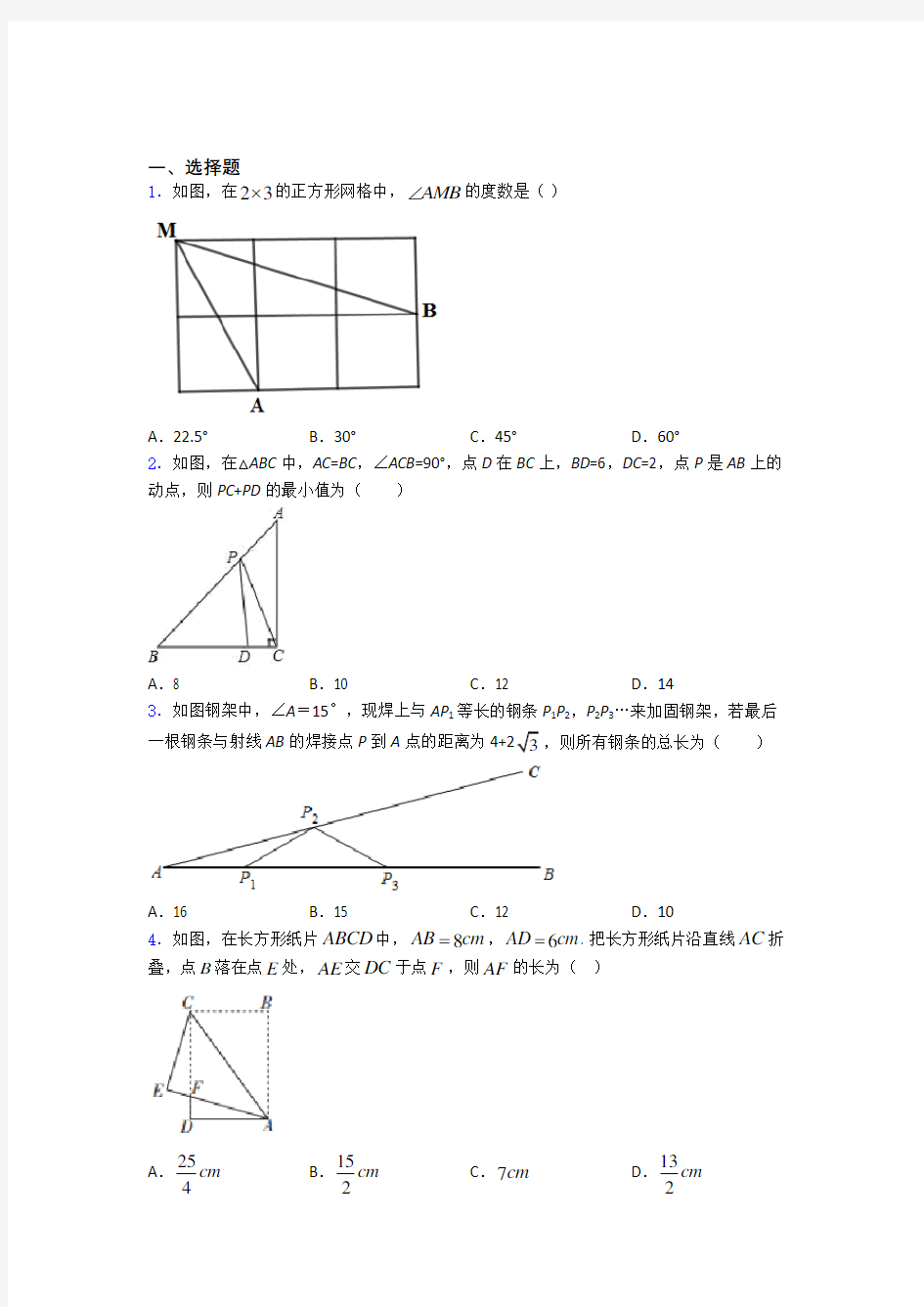
1．如图，在23?的正方形网格中，AMB ∠的度数是（ ）

A ．22.5°

B ．30°

C ．45°

D ．60°

2．如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =6，DC =2，点P 是AB 上的动点，则PC +PD 的最小值为（ ）

A ．8

B ．10

C ．12

D ．14

3．如图钢架中，∠A ＝15°，现焊上与AP 1等长的钢条P 1P 2，P 2P 3…来加固钢架，若最后一根钢条与射线AB 的焊接点P 到A 点的距离为4+23，则所有钢条的总长为（ ）

A ．16

B ．15

C ．12

D ．10

4．如图，在长方形纸片ABCD 中，8AB cm =，6AD cm =. 把长方形纸片沿直线AC 折叠，点B 落在点E 处，AE 交DC 于点F ，则AF 的长为（ ）

A ．

254

cm B ．

152

cm C ．7cm

D ．

132

cm

5．已知等边三角形的边长为a ，则它边上的高、面积分别是（ ）

A ．2,24a a

B ．2

3,24a a

C ．2

33,

24a a D ．2

33,

44

a a 6．已知△ABC 是腰长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，…，依此类推，第n 个等腰直角三角形的面积是( )

A ．2n ﹣2

B ．2n ﹣1

C ．2n

D ．2n+1

7．如图，在四边形ABCD 中，∠ABC =∠ACB =∠ADC =45?，若AD =4，CD =2，则BD 的长为

（ ）

A ．6

B ．27

C ．5

D ．25 8．在△ABC 中，AB =10，BC =12，BC 边上的中线AD =8，则△ABC 边AB 上的高为（ ） A ．8

B ．9.6

C ．10

D ．12

9．如图，在ABC 中，13AB =，10BC =，BC 边上的中线12AD =，请试着判定

ABC 的形状是（ ）

A ．直角三角形

B ．等边三角形

C ．等腰三角形

D ．以上都不对

10．如图，正方体的棱长为4cm ，A 是正方体的一个顶点，B 是侧面正方形对角线的交点．一只蚂蚁在正方体的表面上爬行，从点A 爬到点B 的最短路径是（ ）

A ．9

B ．210

C ．326+

D ．12

二、填空题

11．如图，在平面直角坐标系中，等腰直角三角形OAA 1的直角边OA 在x 轴上，点A 1在第一象限，且OA=1，以点A 1为直角顶点，OA 1为一直角边作等腰直角三角形OA 1A 2，再以点A 2为直角顶点，OA 2为直角边作等腰直角三角形OA 2A 3…依此规律，则点A 2018的坐标是_____．

12．如图，四边形ABDC 中，∠ABD ＝120°，AB ⊥AC ，BD ⊥CD ，AB ＝4，CD ＝43，则该四边形的面积是______．

13．我国古代数学名著《九章算术》中有云：“今有木长二丈，围之三尺．葛生其下，缠木七周，上与木齐．问葛长几何？”大意为：有一根木头长2丈，上、下底面的周长为3尺，葛生长在木下的一方，绕木7周，葛梢与木头上端刚好齐平，则葛长是______尺．(注：l 丈等于10尺，葛缠木以最短的路径向上生长，误差忽略不计)

14．如图，Rt ABC 中，90A ∠=?，8AC =，6AB =，DE AC ⊥，1

3

CD BC =

，

1

3

CE AC

，P 是直线AC 上一点，把CDP 沿DP 所在的直线翻折后，点C 落在直线DE 上的点H 处，CP 的长是__________

15．如图，在Rt △ABC 中，∠ACB ＝90°，AB ＝7.5cm ，AC ＝4.5cm ，动点P 从点B 出发沿射线BC 以2cm/s 的速度移动，设运动的时间为t 秒，当△ABP 为等腰三角形时，t 的取值为_____．

16．在△ABC 中，AB ＝6，AC ＝5，BC 边上的高AD ＝4，则△ABC 的周长为__________. 17．如图，长方形ABCD 中，∠A =∠ABC =∠BCD =∠D =90°，AB =CD =6，AD =BC =10，点E 为射线AD 上的一个动点，若△ABE 与△A ′BE 关于直线BE 对称，当△A ′BC 为直角三角形时，AE 的长为______．

18．如图，长方体纸箱的长、宽、高分别为50cm 、30cm 、60cm ，一只蚂蚁从点A 处沿着纸箱的表面爬到点B 处.蚂蚁爬行的最短路程为_______cm.

19．如图，直线l 上有三个正方形a ，b ，c ，若a ，c 的边长分别为5和12，则b 的面积为_________________.

20．如图，把平面内一条数轴x 绕点O 逆时针旋转角θ（0°＜θ＜90°）得到另一条数轴y ，x 轴和y 轴构成一个平面斜坐标系．规定：已知点P 是平面斜坐标系中任意一点，过点P 作y 轴的平行线交x 轴于点A ，过点P 作x 轴的平行线交y 轴于点B ，若点A 在x 轴上对应的实数为a ，点B 在y 轴上对应的实数为b ，则称有序实数对（a ，b ）为点P 的斜坐标．在平面斜坐标系中，若θ＝45°，点P 的斜坐标为（1，22），点G 的斜坐标为（7，﹣22），连接PG ，则线段PG 的长度是_____．

三、解答题

21．如图，在△ABC 中，AB ＝30 cm ，BC ＝35 cm ，∠B ＝60°，有一动点M 自A 向B 以1 cm/s 的速度运动，动点N 自B 向C 以2 cm/s 的速度运动，若M ，N 同时分别从A ，B 出发．

(1)经过多少秒，△BMN 为等边三角形； (2)经过多少秒，△BMN 为直角三角形．

22．如图，已知ABC ?中，90B ∠=?，8AB cm =，6BC cm =，P 、Q 是ABC ?边上的两个动点，其中点P 从点A 开始沿A B →方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C →方向运动，且速度为每秒2cm ，它们同时出发，设出发的时间为t 秒．

（1）当2t =秒时，求PQ 的长；

（2）求出发时间为几秒时，PQB ?是等腰三角形？

（3）若Q 沿B C A →→方向运动，则当点Q 在边CA 上运动时，求能使BCQ ?成为等腰三角形的运动时间．

23．在等腰△ABC 与等腰△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点D 、E 、C 三点在同一条直线上，连接BD ．

（1）如图1，求证：△ADB ≌△AEC

（2）如图2，当∠BAC ＝∠DAE ＝90°时，试猜想线段AD ，BD ，CD 之间的数量关系，并写出证明过程；

（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为： （不写证明过程）

24．已知ABC ?中，如果过项点B 的一条直线把这个三角形分割成两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为ABC ?的关于点B 的二分割线．例如：如图1，Rt ABC ?中，90A ?∠=，20C ?∠=，若过顶点B 的一条直线BD 交AC 于点D ，若20DBC ?∠=，显然直线BD 是ABC ?的关于点B 的二分割线．

（1）在图2的ABC ?中，20C ?∠=，110ABC ?∠=．请在图2中画出ABC ?关于点B 的二分割线，且DBC ∠角度是 ；

（2）已知20C ?∠=，在图3中画出不同于图1，图2的ABC ?，所画ABC ?同时满足:①C ∠为最小角；②存在关于点B 的二分割线．BAC ∠的度数是 ；

（3）已知C α∠=，ABC ?同时满足：①C ∠为最小角；②存在关于点B 的二分割线．请求出BAC ∠的度数（用α表示）．

25．如图所示，已知ABC ?中，90B ∠=?，16AB cm =，20AC cm =，P 、Q 是

ABC ?的边上的两个动点，其中点P 从点A 开始沿A B →方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C A →→方向运动，且速度为每秒2cm ，它们同时出发，设出发的时间为ts ．

（1）则BC=____________cm；

（2）当t为何值时，点P在边AC的垂直平分线上？此时CQ=_________?

?成为等腰三角形的运动时间．

（3）当点Q在边CA上运动时，直接写出使BCQ

26．如图，点A是射线OE：y＝x（x≥0）上的一个动点，过点A作x轴的垂线，垂足为B，过点B作OA的平行线交∠AOB的平分线于点C．

（1）若OA＝2，求点B的坐标；

（2）如图2，过点C作CG⊥AB于点G，CH⊥OE于点H，求证：CG＝CH．

（3）①若点A的坐标为（2，2），射线OC与AB交于点D，在射线BC上是否存在一点P 使得△ACP与△BDC全等，若存在，请求出点P的坐标；若不存在，请说明理由．

②在（3）①的条件下，在平面内另有三点P122），P2（2，2），P3

（2，22），请你判断也满足△ACP与△BDC全等的点是．（写出你认为正确的点）

27．问题情境：综合实践活动课上，同学们围绕“已知三角形三边的长度，求三角形的面积”开展活动，启航小组同学想到借助正方形网格解决问题

问题解决：图（1）、图（2）都是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，操作发现，启航小组同学在图（1）中画出△ABC，其顶点A，B，C都在格点上，同时构造长方形CDEF，使它的顶点都在格点上，且它的边EF经过点A，ED经过点B．同学们借助此图求出了△ABC的面积．

（1）在图（1）中，△ABC的三边长分别是AB＝，BC＝，AC＝．△ABC 的面积是．

（2）已知△PMN中，PM17，MN＝5NP13

图（2）中画出△PMN，并直接写出△RMN的面积．

28．如图，在平面直角坐标系中，点O 是坐标原点，ABC ?，ADE ?，AFO ?均为等边三角形，A 在y 轴正半轴上，点0()6,B -，点(6,0)C ，点D 在ABC ?内部，点E 在

ABC ?的外部，32=AD ，30DOE ∠=?，OF 与AB 交于点G ，连接DF ，DG ，DO ，OE .

（1）求点A 的坐标；

（2）判断DF 与OE 的数量关系，并说明理由； （3）直接写出ADG ?的周长. 29．（知识背景）

据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连接得到一个直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括为“勾三、股四、弦五”．像3、4、5这样为三边长能构成直角三角形的三个正整数，称为勾股数． （应用举例）

观察3，4，5；5，12，13；7，24，25；…

可以发现这些勾股数的勾都是奇数，且从3起就没有间断过，并且 勾为3时，股14(91)2=

-，弦1

5(91)2=+； 勾为5时，股112(251)2=

-，弦1

13(251)2

=+； 请仿照上面两组样例，用发现的规律填空： （1）如果勾为7，则股24＝ 弦25＝

（2）如果勾用n （3n ≥，且n 为奇数）表示时，请用含有n 的式子表示股和弦，则股＝ ，弦＝ ． （解决问题）

观察4，3，5；6，8，10；8，15，17；…根据应用举例获得的经验进行填空： （3）如果,,a b c 是符合同样规律的一组勾股数，2a m =（m 表示大于1的整数），则

b = ，

c = ，这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式．

（4）请你利用柏拉图公式，补全下面两组勾股数（数据从小到大排列）第一组： 、24、 ：第二组： 、 、37．

30．如图1，已知△ABC 是等边三角形，点D ，E 分别在边BC ，AC 上，且CD ＝AE ，AD 与BE 相交于点F ．

（1）求证：∠ABE ＝∠CAD ；

（2）如图2，以AD 为边向左作等边△ADG ，连接BG ． ⅰ）试判断四边形AGBE 的形状，并说明理由；

ⅱ）若设BD ＝1，DC ＝k （0＜k ＜1），求四边形AGBE 与△ABC 的周长比（用含k 的代数式表示）．

【参考答案】***试卷处理标记，请不要删除

一、选择题 1．C 解析：C 【分析】

连接AB ，求出AB 、BM 、AM 的长，根据勾股定理逆定理即可求证AMB ?为直角三角形，而AM=BM ，即AMB ?为等腰直角三角形，据此即可求解． 【详解】 连接AB

∵22125AM =+=22125AB =+=221310BM =+=∴22210AM AB BM +==∴AMB ?为等腰直角三角形

∴45AMB ∠=? 故选C ． 【点睛】

本题考查了勾股定理的逆定理，重点是求出三条边的长，然后证明AMB ?为直角三角形．

2．B

解析：B 【分析】

过点C 作CO ⊥AB 于O ，延长CO 到C ′，使OC ′＝OC ，连接DC ′，交AB 于P ，连接CP ，此时DP ＋CP ＝DP ＋PC ′＝DC ′的值最小．由DC ＝2，BD ＝6，得到BC ＝8，连接BC ′，由对称性可知∠C ′BA ＝∠CBA ＝45°，于是得到∠CBC ′＝90°，然后根据勾股定理即可得到结论． 【详解】

解：过点C 作CO ⊥AB 于O ，延长CO 到C ′，使OC ′＝OC ，连接DC ′，交AB 于P ，连接CP ．

此时DP ＋CP ＝DP ＋PC ′＝DC ′的值最小． ∵DC ＝2，BD ＝6， ∴BC ＝8，

连接BC ′，由对称性可知∠C ′BA ＝∠CBA ＝45°， ∴∠CBC ′＝90°，

∴BC ′⊥BC ，∠BCC ′＝∠BC ′C ＝45°， ∴BC ＝BC ′＝8，

根据勾股定理可得DC ′＝22228610BC BD '+=+=． 故选：B ．

【点睛】

此题考查了轴对称﹣线路最短的问题，确定动点P 为何位置时 PC ＋PD 的值最小是解题的关键．

3．D

解析：D 【分析】

根据已知利用等腰三角形的性质及三角形外角的性质，找出图中存在的规律，求出钢条的根数，然后根据最后一根钢条与射线AB 的焊接点P 到A 点的距离即AP 5为3AP 1＝a ，作P 2D ⊥AB 于点D ，再用含a 的式子表示出P 1P 3，P 3P 5，从而可求出a 的值，即得

出每根钢条的长度，从而可以求得所有钢条的总长．

【详解】

解：如图，∵AP1与各钢条的长度相等，∴∠A=∠P1P2A=15°，∴∠P2P1P3=30°，∴∠P1P3P2=30°，∴∠P3P2P4=45°，

∴∠P3P4P2=45°，∴∠P4P3P5=60°，∴∠P3P5P4=60°，

∴∠P5P4P6=75°，∴∠P4P6P5=75°，∴∠P6P5B=90°，

此时就不能再往上焊接了，综上所述总共可焊上5根钢条．

设AP1＝a，作P2D⊥AB于点D，

∵∠P2P1D＝30°，∴P2D=1

2P1P2，∴P1D＝

3

a，

∵P1P2=P2P3，∴P1P3＝2P1D =3a，

∵∠P4P3P5=60°，P3P4=P4P5，∴△P4P3P5是等边三角形，∴P3P5＝a，

∵最后一根钢条与射线AB的焊接点P到A点的距离为4+23，

∴AP5=a+3a+a＝4+23，

解得，a＝2，

∴所有钢条的总长为2×5＝10，

故选：D．

【点睛】

本题考查了三角形的内角和、等腰三角形的性质、三角形外角的性质、等边三角形的判定与性质以及勾股定理等知识，发现并利用规律找出钢条的根数是解答本题的关键．

4．A

解析：A

【分析】

由已知条件可证△CFE≌△AFD，得到DF=EF,利用折叠知AE=AB=8cm，设AF=xcm，则DF=(8-x)cm，在Rt△AFD中，利用勾股定理即可求得x的值.

【详解】

∵四边形ABCD是长方形，

∴∠B=∠D=900，BC=AD,

由翻折得AE=AB=8m，∠E=∠B=900,CE=BC=AD

又∵∠CFE=∠AFD

∴△CFE≌△AFD

∴EF=DF

设AF=xcm，则DF=（8-x）cm

在Rt△AFD 中，AF 2=DF 2+AD 2,AD=6cm ，

222(8)6x x =-+

254

x cm =

故选择A. 【点睛】

此题是翻折问题，利用勾股定理求线段的长度.

5．C

解析：C 【分析】

作出等边三角形一边上的高，利用直角三角形中，30°角所对的直角边等于斜边的一半，得出BD ，利用勾股定理即可求出AD ，再利用三角形面积公式即可解决问题． 【详解】

解：如图作AD ⊥BC 于点D ． ∵△ABC 为等边三角形， ∴∠B ＝60°，∠B AD ＝30° ∴1122

BD AB a =

= 由勾股定理得，2222213

()22

AD AB BD a a a =

-=-=

∴边长为a 的等边三角形的面积为12×a ×3a ＝3a 2

， 故选：C ．

【点睛】

本题考点涉及等边三角形的性质、含30°角的直角三角形、勾股定理以及三角形面积公式，熟练掌握相关性质定理是解题关键.

6．A

解析：A 【分析】

连续使用勾股定理求直角边和斜边，然后再求面积，观察发现规律，即可正确作答. 【详解】

解：∵△ABC 是边长为1的等腰直角三角形

1211

11222

ABC S -?∴=??== ，

∴AC 2==

==

2232

1

12:

2

1

22122

AACD ADE S S --?∴====??==

∴第n 个等腰直角三角形的面积是22n - ， 故答案为A. 【点睛】

本题的难点是运用勾股定理求直角三角形的直角边，同时观察、发现也是解答本题的关键.

7．A

解析：A 【解析】

【分析】作AD′⊥AD ，AD′=AD ，连接CD′，DD′，根据等式的性质，可得∠BAD 与∠CAD′的关系，根据SAS ，可得△BAD 与△CAD′的关系，根据全等三角形的性质，可得BD 与CD′的关系，根据勾股定理，可得答案．

【详解】作AD′⊥AD ，AD′=AD ，连接CD′，DD′， 则有∠AD′D=∠D′AD=45?， ∵∠BAC+∠CAD=∠DAD′+∠CAD ， 即∠BAD=∠CAD′，

在△BAD 与△CAD′中，''BC CA BAD CAD AD AD =??

∠=∠??=?

，

∴△BAD ≌△CAD′（SAS ）， ∴BD=CD′，

∠DAD′=90°，由勾股定理得

，

∠D′DA+∠ADC=90°，由勾股定理得

，

故选A.

【点睛】本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质，勾股定理，添加辅助线作出全等图形是解题关键．

8．B

解析：B 【分析】

如图，作CE AB ⊥与E,利用勾股定理的逆定理证明AD BC ⊥,再利用面积法求出EC 即可. 【详解】

如图，作CE AB ⊥与E.

AD 是ABC ?的中线,BC =12, ∴BD=6,

10,8,6,AB AD BD ===

∴ 222AB AD BD =+,

90,ADB ∴∠= ,AD BC ∴⊥

11

,22

ABC S BC AD AB CE ?== 128

9.6.10

CE ?∴=

= 故选B. 【点睛】

本题主要考查勾股定理的逆定理,三角形的面积等知识,解题的关键是熟练掌握基本知识,学会面积法求三角形的高.

9．C

解析：C 【分析】

利用勾股定理的逆定理可以推导出ABD △是直角三角形.再利用勾股定理求出A C ，可得出AB=AC ，即可判断. 【详解】

解：由已知可得CD=BD=5,

22251213+=

即222BD AD AB +=,

ABD ∴是直角三角形，90ADB ∠=?，

90ADC ∴∠=?

222AD CD AC ∴+=

2251213AC ∴=+=

13AB AC ∴==

故ABC 是等腰三角形. 故选C 【点睛】

本题考查了勾股定理和它的逆定理，熟练掌握定理是解题关键.

10．B

解析：B 【分析】

将正方体的左侧面与前面展开，构成一个长方形，用勾股定理求出距离即可． 【详解】

解：如图，AB ＝22(24)2210++=．

故选：B ． 【点睛】

此题求最短路径，我们将平面展开，组成一个直角三角形，利用勾股定理求出斜边就可以了．

二、填空题

11．（0，21009） 【解析】

【分析】本题点A 坐标变化规律要分别从旋转次数与点A 所在象限或坐标轴、点A 到原点的距离与旋转次数的对应关系．

【详解】∵∠OAA 1=90°，OA=AA 1=1，以OA 1为直角边作等腰Rt △OA 1A 2，再以OA 2为直角边

作等腰Rt △OA 2A 3，…，

∴OA 1，OA 2=）2，…，OA 2018=）2018， ∵A 1、A 2、…，每8个一循环， ∵2018=252×8+2

∴点A 2018的在y 轴正半轴上，OA 2018=2018

=21009，

故答案为（0，21009）.

【点睛】本题是平面直角坐标系下的规律探究题，除了研究动点变化的相关数据规律，还应该注意象限符号．

12． 【分析】

延长CA 、DB 交于点E ，则60C ∠=°，30E ∠=?，在Rt ABE ?中，利用含30角的直

角三角形的性质求出28BE AB ==，根据勾股定理求出AE =．同理，在Rt DEC ?中

求出2CE CD ==12DE ==，然后根据CDE ABE ABDC S S S ??=-四边形，计算即可求解． 【详解】

解：如图，延长CA 、DB 交于点E ，

∵四边形ABDC 中，120ABD ∠=?，AB AC ⊥，BD CD ⊥， ∴60C ∠=°， ∴30E ∠=?， 在Rt ABE ?中，

4AB =，30E ∠=?，

∴28BE AB ==，

AE ∴=．

在Rt DEC ?中，

30E ∠=?，CD =

2CE CD ∴==

12DE ∴=，

∴1

42

ABE S ?=??=

1

122

CDE S ?=?=

CDE ABE ABDC S S S ??∴=-=四边形．

故答案为：

【点睛】

本题考查了勾股定理，含30角的直角三角形的性质，图形的面积，准确作出辅助线构造直角三角形是解题的关键．

13．【分析】

这种立体图形求最短路径问题，可以展开成为平面内的问题解决，展开后可转化下图，所以是个直角三角形求斜边的问题，根据勾股定理可求出．

【详解】

解：如图，一条直角边（即木棍的高）长20尺，

另一条直角边长7×3=21（尺），

22

2021

=29（尺）．

答：葛藤长29尺．

故答案为：29．

【点睛】

本题考查了平面展开最短路径问题，关键是把立体图形展成平面图形，本题是展成平面图形后为直角三角形按照勾股定理可求出解．

14．5

3

或

20

3

【分析】

根据折叠后点C的对应点H与AC的位置关系分类讨论，分别画出对应的图形，利用勾股定理求出各边的长，再根据折叠的性质与勾股定理列出对应的方程即可求出结论．

【详解】

解：①当折叠后点C的对应点H在AC的下方时，如下图所示

∵Rt ABC 中，90A ∠=?，8AC =，6AB =， 根据勾股定理可得BC=2210AB AC +=

∵1

3CD BC =，13

CE AC =， ∴13CD BC =

=103，13

CE AC ==83

∵DE AC ⊥

根据勾股定理可得DE=222CD CE -= 由折叠的性质可得：DH=CD=10

3

，CP=PH ∴EH=DH －DE=

43

设CP=PH=x ，则EP=CE －CP=8

3

－x

在Rt △PEH 中，EP 2＋EH 2=PH 2

即（8

3－x ）2＋（43

）2=x 2

解得：x=

5

3 即此时CP=

53

； ②当折叠后点C 的对应点H 在AC 的上方时，如下图所示

根据折叠的性质可得DH=CD=10

3

，CP=PH

∴EH=DH＋DE=16 3

设CP=PH=y，则EP= CP－CE =y－8 3

在Rt△PEH中，EP2＋EH2=PH2

即（y－8

3

）2＋（

16

3

）2=y2

解得：y=20 3

即此时CP=20

3

．

综上所述：CP=5

3

或

20

3

．

故答案为：5

3

或

20

3

．

【点睛】

此题考查的是勾股定理和折叠问题，掌握利用勾股定理解直角三角形、折叠的性质和分类讨论的数学思想是解决此题的关键．

15．75或6或9 4

【分析】

当△ABP为等腰三角形时，分三种情况：①当AB＝BP时；②当AB＝AP时；③当BP＝AP 时，分别求出BP的长度，继而可求得t值．

【详解】

在Rt△ABC中，BC2＝AB2﹣AC2＝7.52﹣4.52＝36，

∴BC＝6（cm）；

①当AB＝BP＝7.5cm时，如图1，t＝7.5

2

＝3.75（秒）；

②当AB＝AP＝7.5cm时，如图2，BP＝2BC＝12cm，t＝6（秒）；

③当BP＝AP时，如图3，AP＝BP＝2tcm，CP＝（4.5﹣2t）cm，AC＝4.5cm，在Rt△ACP中，AP2＝AC2+CP2，

所以4t2＝4.52+（4.5﹣2t）2，

解得：t＝9

4

，

综上所述：当△ABP为等腰三角形时，t＝3.75或t＝6或t＝9

4

．

故答案为：3.75或6或9

4

．

【点睛】

此题是等腰三角形与动点问题，考查等腰三角形的性质，勾股定理，解题中应根据每两条边相等分情况来解答，不要漏解. 16．1425+或825+ 【分析】

分两种情况考虑：如图1所示，此时△ABC 为锐角三角形，在直角三角形ABD 与直角三角形ACD 中，利用勾股定理求出BD 与DC 的长，由BD+DC 求出BC 的长，即可求出周长；如图2所示，此时△ABC 为钝角三角形，同理由BD -CD 求出BC 的长，即可求出周长． 【详解】

解：分两种情况考虑：

如图1所示，此时△ABC 为锐角三角形，

在Rt △ABD 中，根据勾股定理得：BD=22226425AB AD -=-=， 在Rt △ACD 中，根据勾股定理得：CD=2222543AC AD -=-=，

∴BC=253+，

∴△ABC 的周长为：652531425+++=+； 如图2所示，此时△ABC 为钝角三角形，

在Rt △ABD 中，根据勾股定理得：22226425AB AD -=-= 在Rt △ACD 中，根据勾股定理得：2222543AC AD --=，

∴BC=253-，

∴△ABC 的周长为：65253825++=+