数学建模之微分方程建模与平衡点理论

微分方程
列微分方程常用的方法: (1)根据规律列方程
利用数学、力学、物理、化学等学科中的定理或经过实验检验的规律来建立微分方程模型。 (2)微元分析法
利用已知的定理与规律寻找微元之间的关系式,与第一种方法不同的是对微元而不是直接对函数及其导数应用规律。 (3)模拟近似法
在生物、经济等学科的实际问题中,许多现象的规律性不很清楚,即使有所了解也是极其复杂的,建模时在不同的假设下去模拟实际的现象,建立能近似反映问题的微分方程,然后从数学上求解或分析所建方程及其解的性质,再去同实际情况对比,检验此模型能否刻画、模拟某些实际现象。
一、模型的建立与求解
传染病模型
(1)基础模型
假设:t 时刻病人人数()x t 连续可微。每天每个病人有效接触(使病人治病的接触)的人数为λ,0t =时有0x 个病人。 建模:t 到t t +?病人人数增加
()()()x t t x t x t t λ+?-=? (1)
0,(0)dx
x x x dt
λ== (2) 解得:
0()t x t x e λ= (3)
所以,病人人数会随着t 的增加而无限增长,结论不符合实际。 (2)SI 模型
假设:1.疾病传播时期,总人数N 保持不变。人群分为两类,健康者占总人数的比例为s(t),病人占总人数的比例为i(t)。
2.每位病人每天平均有效接触λ人,λ为日接触率。有效接触后健康者变为病人。
依据:患病人数的变化率=Ni(t)(原患病人数)* λs(t)(每个病人每天使健康人变为病人的人数) 建模:
di
N
Nsi dt
λ= (4) 由于
()()1s t i t += (5)
设t=0时刻病人所占的比例为0i ,则可建立Logistic 模型
0(1),(0)di
i i i i dt
λ=-= (6) 解得:
01()111kt
i t e i -=
??+- ???
(7)
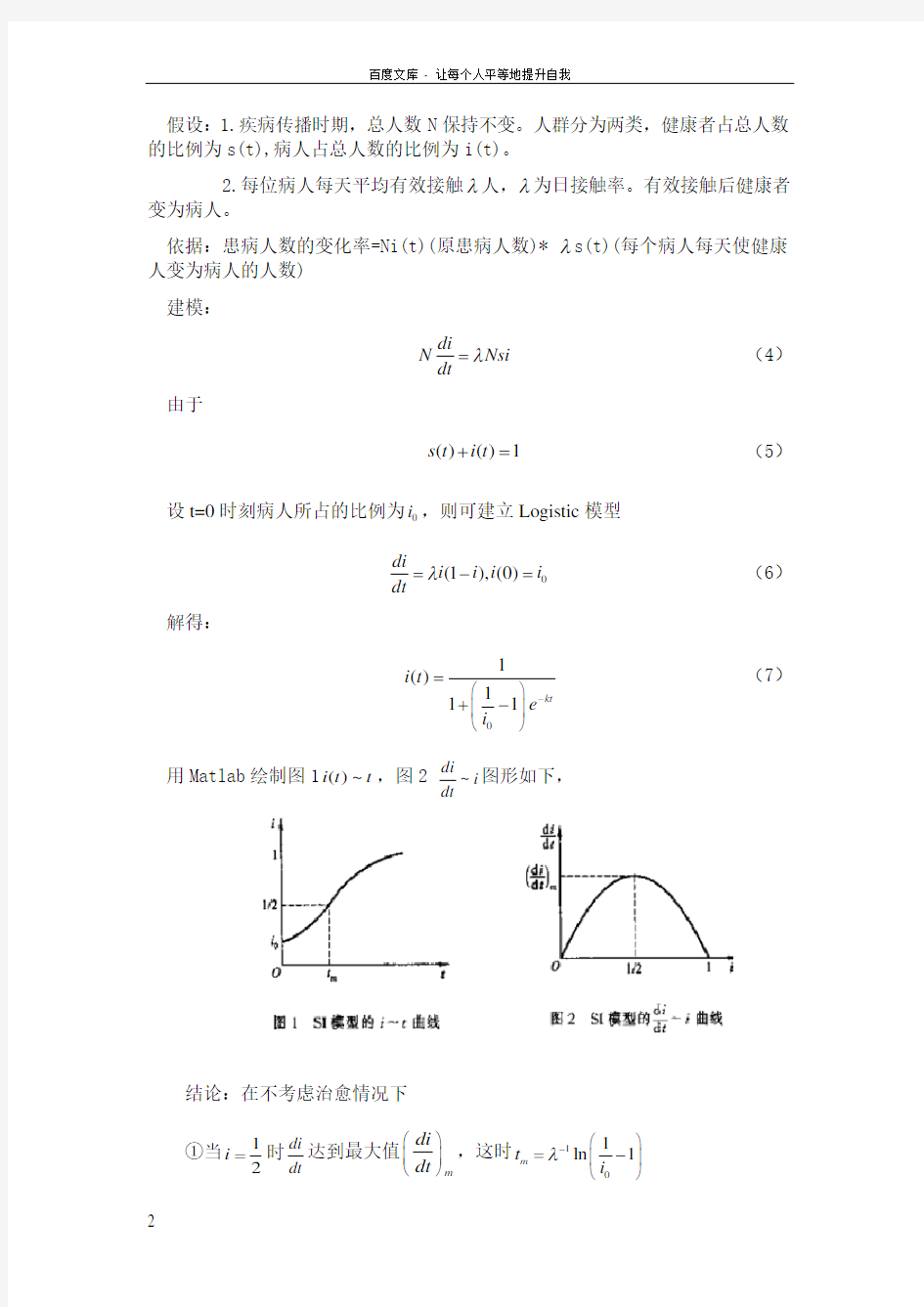
用Matlab 绘制图1()~i t t ,图2
~di
i dt
图形如下,
结论:在不考虑治愈情况下 ①当12i =
时di
dt 达到最大值m di dt ?? ???,这时101ln 1m t i λ-??=- ???
②t →∞时人类全被感染。未考虑治愈情况。 (3)SIS 模型
假设:1.疾病传播时期,总人数N 保持不变。人群分为两类,健康者占总人数
的比例为s(t),病人占总人数的比例为i(t)。 2.每位病人每天平均有效接触λ人,λ为日接触率。有效接触后健康者
变为病人。 3.在所有病人中,每天有比例μ的人能被治愈,治愈后看作可被感染的
健康者,传染病的平均传染期为
1
μ
。
依据:患病人数的变化率= Nsi λ(患病人数的变化率)-Ni μ(治愈率) 建模:
di
N
Nsi Ni dt
λμ=- (8)
0(1),(0)di
i i i i i dt
λμ=-- = (9) 令σ为整个传染期内每位病人有效接触的平均人数,σλμ=。 则有
11di
i i dt λσ????=--- ???????
(10) 用Matlab 绘制出
~di
i dt
(图3,图5)和 i~t (图4,图6)。
结论:1σ=为一个阈值。 ①1σ>,()i t 极限值1
()1i σ
∞=-
为增函数,()i t 的增减性由0i 的大小确定。
②1σ≤,病人比例()i t 越来越小,最终趋于0。
(4)SIR 模型(某些疾病患者治愈后获得了很强的免疫力,不会再次被感染) 假设:①总人数N 不变,将人群分为健康者,病人,和病愈免疫的移除者,他
们在总人数中所占的比例依次为()s t ,()i t ,()r t 。
②λ为病人的日接触率,μ为日治愈率,σλμ=为传染期接触数。
建模:由假设1得
()()()1s t i t r t ++= (11)
dr
N
Ni dt
μ= (12) 令t=0时健康者与病人所占比例分别为0000(0),(0)s s i i >>,则有
00
,(0),(0)di
si i i i dt ds si s s dt
λμλ?=-=???
?=-=?? (13)
利用Matlab 绘制出()i t ,()s t (图7),~i s (图8)图形,~i s 图形称为相轨线。
相轨线分析:利用相轨线讨论解()i t ,()s t 的性质。
~s i 平面称为相平面,相轨线在其上的定义域为(,)s i D ∈为
(){},0,0,1D s i s i s i =≥≥+≤ (14)
消去方程中的dt ,并由σ得到
011,s s di i
i ds s
σ==-= (15)
解得:
()000
1ln s
i s i s s σ=+-+
(16) 在定义域D 内,相轨线是上式所表示的曲线,如图9所示,其中箭头表示随着时间t 的增加()s t 和()i t 的变化趋势。下面分析()s t 、()i t 和()r t 的变化情况(t →∞时它们的极限值分别记做,s i ∞∞和r ∞)
①不论初始条件00,s i 如何,病人最终会消失,0i ∞= ,证明:
首先,由式(13),
0ds dt ≤,而()0s t ≥,所以s ∞存在;由式(11),0dr dt
≥,而()1r t ≤,所以r ∞存在;由式(11)得i ∞存在。
其次,若0i ε∞
=>,则由式(11),对于充分大的t 有2
dr
dt
ε
μ
>,导致r ∞
=∞,
与r ∞存在相矛盾。
从图形来看,无论相轨线从何点出发,最终都将与s 轴相交。
②令式(16)中0i =,则最终未被感染的健康者的比例是s ∞,s ∞为方程
000
1ln 0s s i s s σ∞
∞+-+
= (17) 在(0,1/)σ内的根,在图形上表示为相轨线与s 轴在(0,1/)σ内交点的横坐标。 ③若0
1/s σ>,则()i t 先增加,当1/s σ=时,()i t 达到最大值
0001
(1ln )i s i s σσ
∞=+-
+ (18)
然后()i t 减小且趋于0,()s t 单调减小至s ∞,如图中由1P 出发的相轨线。 ④若0
1/s σ≤,则()i t 单调减小至0,()s t 单调减小至s ∞,如图中由2P 出发的
相轨线。 结论:①若病人比例有一段时间增长即认为传染病在蔓延,则1/σ为一个阈值,
01/s σ>时蔓延。可以通过减小σ 使01/s σ≤,使传染病不蔓延。
②0
1/s σ>,σ减小时,s ∞增加,也能控制蔓延程度。
捕鱼模型
考察一个渔场,其中鱼量在天然环境下按一定规律增长、如果捕捞量恰好等于增长量,那么渔场鱼量将保持不变,这个捕捞量就可以持续. ①产量模型
假设:()x t 为渔场中鱼量。
1.无捕捞时,鱼的的增长服从logistic 规律,即 ()()1x x t f x rx N ??
==-
???
(19)其中:r 表示固有增长率,N 表示环境容许的最大鱼量,()f x 表示单位时间的增长量。
2. 用E 表示单位时间捕捞率,单位时间捕捞量和渔场鱼量()x t 成正比,则有
单位时间捕捞量为
()h x Ex = (20)
建模:捕捞情况下渔场鱼量满足
()()1x x t F x rx Ex N ?
?==-- ???
(21)
其中:()()()F x f x h x =-。
判断()x t 的稳定条件,求式(21)的平衡点,分析其稳定性。 令式(21)为0,得两个平衡点:
01(1),0E x N x r
=-
= (22)
稳定性判断
01(),()F x E r F x r E ''=-=-
当E r <时01()0,()0F x F x ''<>,则0x 点稳定,1x 点不稳定。 当E r >时01()0,()0F x F x ''><,则1x 点稳定,0x 点不稳定。 分析:用E 表示捕捞率,r 表示固有增长率。 ①当E r <时,可使鱼量稳定在0x ,获得稳定产量。 ②当E r >时,1x 稳定,渔场干枯。
根据(19),(20)式分别绘制曲线()y f x =及()()y h x E x ==,使用Matlab 绘制图形如下所示,
得两曲线交点为P ,则P 横坐标为稳定平衡点0x ,纵坐标为稳定条件下单位时间的产量,当交点位于抛物线顶点时获得最大的持续产量,此时的稳定平衡点为
*02N x =
, 单位时间的最大持续产量为4m rN h =,捕捞率*2
r
E =。 结论:将捕捞率控制在固有增长率r 的一半,即使渔场鱼量保持在最大鱼量的一半时,能够获得最大的持续产量。
②效益模型(经济效益=总收入收入-成本)
假设:鱼销售单价p ,单位捕捞率费用是c ,单位时间收入为T ,成本为
S ,单位利润为R ,则有
()T ph x pEx
S cE
R T S pEx cE ====-=- (23)
建模:在稳定条件0x x =下,将式(22)代入式(23)得
()()()(1)E
R E T E S E pNE cE r
=-=-
- (24) 求出使利润最大的捕捞强度为
12R r c E pN ??=- ???
(25)
最大利润下的渔场稳定鱼量R x 和单位时间的持续产量R h 22R N c
x p
=
+ (26) 2
22
(1)14R R R x rN c h rx N p N
??
=-=- ???
(27) 结论:当有最大效益时,捕捞率和持续产量都减小,渔场应保持的稳定鱼量增
加,捕捞成本越大或销售价格越低所需减少增大的部分越大。
③捕捞过度:封闭式捕捞追求利益最大,开放式捕捞只追求利润。 令式(24)中()0R E =,解S E ,则
1S c E r pN ??
=- ???
(28)
当S E E <时,利润()0R E >经营者加大捕捞强度,当S E E >,()0R E <经营者减小捕捞强度,S E 为盲目捕捞下的临界强度。
或利用Matlab 绘制~(),()E T E S E 曲线如图(12),则(),()T E S E 交点横坐标即为S E 。
二、微分方程与平衡点理论
一阶微分方程
设一阶微分方程为
()()x t f x = (1)
求解方程()=0f x 即可出平衡点0x x =。再判断平衡点0x 是否稳定。 判断平衡点的常用方法有以下两种 (1)直接法
将()f x 在0x 点作泰勒展开,仅取一次项,则得方程(1)的近似线性方程为
()()()'0x t f x x x =- (2)
所以,0x 也是方程(2)的平衡点。令()'0=f x a ,则方程(2)的一般解为
()0
at x t ce x c =+为常数
对于0x 点的稳定性有如下结论:
如果()'00f x <,则0x 对于方程(2)和(1)都是稳定的; 如果()'00f x >,则0x 对于方程(2)和(1)都是不稳定的; (2)间接法
如果存在0x 某个邻域内的任意值,使方程(1)的解()x t 满足
()0lim t x t x →∞
= (3)
那么0x 是稳定的,否则0x 是不稳定的。 二阶微分方程
设二阶微分方程为
()()()()
112212,,x t f x x x t g x x =???=?? (4) 求出方程()()
1212,0,0f x x g x x =???=??的解,即为二阶微分方程的平衡点00
1122,x x x x ==记作
()00
012P x x ,
利用直接法判断平衡点的稳定性,由线性常系数微分方程组
()()11122
21122
x t a x a x x t b x b x =+???
=+?? (5) 得系数矩阵记
1212=a a A b b ??
????
(6) 为求出方程(5)的惟一平衡点()00
0P ,的稳定性,令A 的行列式为 det 0A ≠ (7)
()000P ,的稳定性可由方程(5)的特征方程的根λ决定。即
()det =0A I λ- (8)
方程(8)可以写为
()2120det p q p a b q A λλ?++=?
=-+??=?
(9) 用12,λλ表示特征根,则(2121
,=-42
p p q λλ-。 方程(5)的一般解形式为
()()12121212121212,,t t t t c e c e c e c te c c λλλλλλλλ+≠+=或为任意常数
则当12,λλ是负数或者有负实部时,()000P ,为稳定平衡点;当12,λλ有一个正数或者有正实部时,()00
0P ,为不稳定平衡点。在(7)的约束下12,λλ不可能为0。
常微分方程在数学建模中的应用(免费版)
常微分方程在数学建模中的应用 这里介绍几个典型的用微分方程建立数学模型的例子. 一、人口预测模型 由于资源的有限性,当今世界各国都注意有计划地控制人口的增长,为了得到人口预测模型,必须首先搞清影响人口增长的因素,而影响人口增长的因素很多,如人口的自然出生率、人口的自然死亡率、人口的迁移、自然灾害、战争等诸多因素,如果一开始就把所有因素都考虑进去,则无从下手.因此,先把问题简化,建立比较粗糙的模型,再逐步修改,得到较完善的模型. 例1( 马尔萨斯 (Malthus ) 模型) 英国人口统计学家马尔萨斯(1766—1834)在担任牧师期间,查看了教堂100多年人口出生统计资料,发现人口出生率是一个常数,于1789年在《人口原理》一书中提出了闻名于世的马尔萨斯人口模型,他的基本假设是:在人口自然增长过程中,净相对增长(出生率与死亡率之差)是常数,即单位时间内人口的增长量与人口成正比,比例系数设为r ,在此假设下,推导并求解人口随时间变化的数学模型. 解 设时刻t 的人口为)(t N ,把)(t N 当作连续、可微函数处理(因人口总数很大,可近似地这样处理,此乃离散变量连续化处理),据马尔萨斯的假设,在t 到t t ?+时间段内,人口的增长量为 t t rN t N t t N ?=-?+)()()(, 并设0t t =时刻的人口为0N ,于是 ?????==. , 00)(d d N t N rN t N 这就是马尔萨斯人口模型,用分离变量法易求出其解为 )(00e )(t t r N t N -=, 此式表明人口以指数规律随时间无限增长. 模型检验:据估计1961年地球上的人口总数为9 1006.3?,而在以后7年中,人口总数以每年2%的速度增长,这样19610=t ,901006.3?=N ,02.0=r ,于是 ) 1961(02.09 e 1006.3)(-?=t t N . 这个公式非常准确地反映了在1700—1961年间世界人口总数.因为,这期间地球上的人 口大约每35年翻一番,而上式断定34.6年增加一倍(请读者证明这一点). 但是,后来人们以美国人口为例,用马尔萨斯模型计算结果与人口资料比较,却发现有很大的差异,尤其是在用此模型预测较遥远的未来地球人口总数时,发现更令人不可思议的问题,如按此模型计算,到2670年,地球上将有36 000亿人口.如果地球表面全是陆地(事实上,地球表面还有80%被水覆盖),我们也只得互相踩着肩膀站成两层了,这是非常荒谬的,因此,这一模型应该修改. 例2(逻辑Logistic 模型) 马尔萨斯模型为什么不能预测未来的人口呢?这主要是地
数学建模作业、微分方程实验、北京工业大学
2微分方程实验 1、微分方程稳定性分析 绘出下列自治系统相应的轨线,并标出随 t 增加的运动方向,确定平■衡点, 并按稳定的、渐近稳定的、或不稳定的进行分类: 解:(1)由 f (x ) =x=0, f (y ) =y=0;可得平衡点为(0,0), ___ 1 0 系数矩阵A ,求得特征值入1=1,入2=1; 0 1 p=-(入1+入2)=-2<0 , q=入1入2=1>0;对照稳定性的情况表,可知平■衡点(0, 0) 是 不稳定的。 图形如下: (2)如上题可求得平衡点为(0,0 ),特征值入1=-1,入2=2; p=-(入1+入2)=-1<0 , q-入1入2=-2<0;对照稳定性的情况表,可知平■衡点(0, 0) 是 不稳定的。 其图形如下: dx ⑴dt dt x, y; dx dt dy dt dx x, ⑶尸 2y ;晋 dx y , (4) ? 2x;也 dt x+1, 2y.
(3) 如上题可求得平■衡点为(0,0 ),特征值入1=0 + 1.4142i,入2=0 -1.4142i; p=-(入1+入2)= 0, q-入1入2=1.4142>0;对照稳定性的情况表,可知平■衡点(0, 0)是不稳定的。 其图形如下: (4) 如上题可求得平衡点为(1,0 ),特征值入1=-1,入2=-2; p=-(入1+入2)= 3>0, q=入1入2=2>0;对照稳定性的情况表,可知平■衡点(1, 0) 是稳定的。 其图形如下:
2、种群增长模型 一个片子上的一群病菌趋向丁繁殖成一个圆菌落.设病菌的数目为N,单位 成员的增长率为r1,则由Malthus生长律有竺r1 N,但是,处丁周界表面的dt 那些病菌由丁寒冷而受到损伤,它们死亡的数量与N2成比例,其比例系数为r2, 求N满足的微分方程.不用求解,图示其解族.方程是否有平衡解,如果有,是否为稳定的? 解:由题意很容易列出N满足的微分方程:坐r1N r2N; f(N) dt 令f(N)=O,可求得方程的两个平■衡点N1=0,N2=「22/r i2 1 1 d2N 1 5 5 2 (r1 r2N 2) (r1N r2N 2) dt 2 进而求得 A d2N 令r dt 2 2 0可求得N=r2 /4r〔 则N=N1 N=N2 N=r22/4r i2可以把第一象限划为三部分,且从下到上三部分中分 0,冬dt2 .2 2 c dN cdN c dN cdN 0, ;—0, —r 0; —0, ―r dt dt dt dt 则可以画出N (t) 的图形,即微分方程的解族,如下图所示:
常微分方程在数学建模中的应用.
微分方程应用 1 引言 常微分方程的形成与发展和很多学科有着密切的联系,例如力学、天文学、物理学等.数学的其他分支的快速发展,产生出很多新兴学科,这些新兴学科的产生都对常微分方程的发展有着深刻的影响,而且当前计算机的快速发展更是为常微分方程的应用及理论研究提供了非常有力的工具. 数学解决实际问题就必须建立模型,而数学建模就是把数学语言描述实际现象的过程.利用数学去解决各类实际问题时,建立数学模型是十分重要的一步,但是也是最困难的一步.建立数学模型的过程,是把错综复杂的实际问题简化、抽象为合理的数学结构的过程.要通过大量调查、收集相关数据资料,观察和研究实际对象的固有特征和内在规律,抓住问题的主要矛盾,建立起反映实际问题的数量关系,然后利用数学的理论和方法去分析和解决问题. 因此本文先简要介绍了如何建立微分方程模型,并通过具体的实例来简单地介绍了微分方程在数学建模中的应用. 2 数学模型简介 通常我们把现实问题的一个模拟称为模型.如交通图、地质图、航空模型和建筑模型等.利用字母、数学及其它数学符号建立起来的等式或不等式以及图表、图象、框图等来模拟现实的模型称为数学模型.数学模型在实际生活中经常碰到,如求不规则图形的面积,可建立定积分的数学模型,求变化率的问题可建立导数模型,统计学中抽样调查,买彩票中奖的概率问题等等.学会建立数学模型对解决实际生活问题会有很大的帮助. 建立数学模型是沟通摆在面前的实际问题与数学工具之间联系的一座必不可少的桥梁.随着科学技术的进步,特别是电子计算机技术的迅速发展,数学已经渗透到从自然科学技术到工农业生产建设,从经济生活到社会生活的各个领域.一般地说,当实际问题需要我们对所研究的现实对象提供分析、预报、决策、控制等方面的定量结果时,往往都离不开数学的应用,而建立数学模型则是这个过程的关键环节. 3 常微分方程模型 3.1 常微分方程的简介
数学建模——微分方程的应用
第八节 数学建模——微分方程的应用举例 微分方程在物理学、力学、经济学和管理科学等实际问题中具有广泛的应用,本节我们将集中讨论微分方程的实际应用,尤其是微分方程经济学中的应用. 读者可从中感受到应用数学建模的理论和方法解决实际问题的魅力. 分布图示 ★衰变问题 ★逻辑斯谛方程 ★价格调整问题 ★人才分配问题 内容要点: 一、衰变问题 镭、铀等放射性元素因不断放射出各种射线而逐渐减少其质量, 这种现象称为放射性物质的衰变. 根据实验得知, 衰变速度与现存物质的质量成正比, 求放射性元素在时刻t 的质量. 用x 表示该放射性物质在时刻t 的质量, 则 dt dx 表示x 在时刻t 的衰变速度, 于是“衰变速度与现存的质量成正比”可表示为 .kx dt dx -= (8.1) 这是一个以x 为未知函数的一阶方程, 它就是放射性元素衰变的数学模型, 其中0>k 是比例常数, 称为衰变常数, 因元素的不同而异. 方程右端的负号表示当时间t 增加时, 质量x 减少. 解方程(8.1)得通解.kt Ce x -=若已知当0t t =时, ,0x x =代入通解kt Ce x -=中可得,00kt e x C -= 则可得到方程(8.1)特解 ,)(00t t k e x x --= 它反映了某种放射性元素衰变的规律. 注: 物理学中, 我们称放射性物质从最初的质量到衰变为该质量自身的一半所花费的时间为半衰期, 不同物质的半衰期差别极大. 如铀的普通同位素( U 238)的半衰期约为50亿年;通常的镭( Ra 226)的半衰期是上述放射性物质的特征, 然而半衰期却不依赖于该物质的初始量, 一克Ra 226 衰变成半克所需要的时间与一吨Ra 226衰变成半吨所需要的时间同样都是1600年, 正是这种事实才构成了确定考古发现日期时使用的著名的碳-14测验的基础.
数学建模之微分方程建模与平衡点理论
微分方程 列微分方程常用的方法: (1)根据规律列方程 利用数学、力学、物理、化学等学科中的定理或经过实验检验的规律来建 立微分方程模型。 (2)微元分析法 利用已知的定理与规律寻找微元之间的关系式,与第一种方法不同的是对 微元而不是直接对函数及其导数应用规律。 (3)模拟近似法 在生物、经济等学科的实际问题中,许多现象的规律性不很清楚,即使有 所了解也是极其复杂的,建模时在不同的假设下去模拟实际的现象,建立能 近似反映问题的微分方程,然后从数学上求解或分析所建方程及其解的性 质,再去同实际情况对比,检验此模型能否刻画、模拟某些实际现象。 一、模型的建立与求解 1.1传染病模型 (1)基础模型 假设:t时刻病人人数() x t连续可微。每天每个病人有效接触(使病人治病的接触)的人数为λ,0 t=时有0x个病人。 +?病人人数增加 建模:t到t t
()()()x t t x t x t t λ+?-=? (1) 0,(0)dx x x x dt λ== (2) 解得: 0()t x t x e λ= (3) 所以,病人人数会随着t 的增加而无限增长,结论不符合实际。 (2)SI 模型 假设:1.疾病传播时期,总人数N 保持不变。人群分为两类,健康者占总人数的比例为s(t),病人占总人数的比例为i(t)。 2.每位病人每天平均有效接触λ人,λ为日接触率。有效接触后健康者变为病人。 依据:患病人数的变化率=Ni(t)(原患病人数)* λs(t)(每个病人每天使健康人变为病人的人数) 建模: di N Nsi dt λ= (4) 由于 ()()1s t i t += (5) 设t=0时刻病人所占的比例为0i ,则可建立Logistic 模型 0(1),(0)di i i i i dt λ=-= (6)
最新31微分方程与微分方程建模法汇总
31微分方程与微分方 程建模法
第三章微分方程模型 3.1微分方程与微分方程建模法 一、微分方程知识简介 我们要掌握常微分方程的一些基础知识,对一些可以求解的微分方程及其方程组,要求掌握其解法,并了解一些方程的近似解法。 微分方程的体系:(1)初等积分法(一阶方程及几类可降阶为一阶的方程) ?Skip Record If...?(2)一阶线性微分方程组(常系数线性微分方程组的解法) ?Skip Record If...?(3)高阶线性微分方程(高阶线性常系数微分方程解法)。其中还包括了常微分方程的基本定理。 0.常数变易法:常数变易法在上面的(1)(2)(3)三部分中都出现过,它是由线性齐次方程(一阶或高阶)或方程组的解经常数变易后求相应的非齐次方程或方程组的解的一种方法。 1.初等积分法:掌握变量可分离方程、齐次方程的解法,掌握线性方程的解法,掌握全微分方程(含积分因子)的解法,会一些一阶隐式微分方程的解法(参数法),会几类可以降阶的高阶方程的解法(恰当导数方程)。 分离变量法:(1)可分离变量方程: ?Skip Record If...? (2) 齐次方程:?Skip Record If...? 常数变易法:(1) 线性方程,?Skip Record If...??Skip Record If...?
(2) 伯努里方程,?Skip Record If...??Skip Record If...? 积分因子法:化为全微分方程,按全微分方程求解。 对于一阶隐式微分方程?Skip Record If...?有 参数法:(1) 不含x或y的方程:?Skip Record If...? (2) 可解出x或y的方程:?Skip Record If...? 对于高阶方程,有 降阶法:?Skip Record If...? 恰当导数方程 一阶方程的应用问题(即建模问题)。 2.一阶线性微分方程组:本部分主要内容有:一是一阶线性微分方程组的基本理论(线性齐次、非齐次微分方程组的通解结构,刘维尔公式等),二是常系数线性微分方程组的解法(求特征根,单根与重根[待定系数法]),三是常数变易法。本部分内容与线性代数关系密切,如线性空间,向量的线性相关与线性无关,基与维数,特征方程、特征根与特征向量,矩阵的若当标准型等。3.高阶线性微分方程:了解高阶线性微分方程的基本理论(线性齐次、非齐次微分方程的通解结构,刘维尔公式等); n阶线性常系数微分方程解法:(1)求常系数齐次线性微分方程基本解组的待定指数函数法;(2)求一般非齐次线性方程解的常数变易法;(3)求特
数学建模之微分方程建模与平衡点理论
微分方程 列微分方程常用的方法: (1)根据规律列方程 利用数学、力学、物理、化学等学科中的定理或经过实验检验的规律来建立微分方程模型。 (2)微元分析法 利用已知的定理与规律寻找微元之间的关系式,与第一种方法不同的是对微元而不是直接对函数及其导数应用规律。 (3)模拟近似法 在生物、经济等学科的实际问题中,许多现象的规律性不很清楚,即使有所了解也是极其复杂的,建模时在不同的假设下去模拟实际的现象,建立能近似反映问题的微分方程,然后从数学上求解或分析所建方程及其解的性质,再去同实际情况对比,检验此模型能否刻画、模拟某些实际现象。 一、模型的建立与求解 1.1传染病模型 (1)基础模型 假设:t 时刻病人人数()x t 连续可微。每天每个病人有效接触(使病人治病的接触)的人数为λ,0t =时有0x 个病人。 建模:t 到t t +?病人人数增加 ()()()x t t x t x t t λ+?-=?(1) 0,(0)dx x x x dt λ==(2) 解得: 0()t x t x e λ=(3) 所以,病人人数会随着t 的增加而无限增长,结论不符合实际。 (2)SI 模型
假设:1.疾病传播时期,总人数N 保持不变。人群分为两类,健康者占总人数的比例为s(t),病人占总人数的比例为i(t)。 2.每位病人每天平均有效接触λ人,λ为日接触率。有效接触后健康者变为病人。 依据:患病人数的变化率=Ni(t)(原患病人数)*λs(t)(每个病人每天使健康人变为病人的人数) 建模: di N Nsi dt λ=(4) 由于 ()()1s t i t +=(5) 设t=0时刻病人所占的比例为0i ,则可建立Logistic 模型 0(1),(0)di i i i i dt λ=-=(6) 解得: 01()111kt i t e i -= ??+- ??? (7) 用Matlab 绘制图1()~i t t ,图2 ~di i dt 图形如下, 结论:在不考虑治愈情况下
第三讲微分方程的理论与数学建模
第三讲 微分方程的理论与数学建模 一、微分方程模型的建立 函数是事物的内部联系在数量方面的反映,如何寻找变量之间的函数关系,在实际应用中具有重要意义。在许多实际问题中,往往不能直接找出变量之间的函数关系,但是根据问题所提供的情况,有时可以列出含有要找的函数及其导数的关系式。这就是所谓的微分方程,从而得出微分方程模型。 例1 物体冷却过程的数学模型 将物体放置于空气中,在时刻0=t 时,测量得它的温度为1500=u C ,10分钟后测量得温度为 C u 1001=。我们要求此物体的温度u 和时间t 的关系,并计算20分钟后物体的温度。这里我们假定 空气温度保持为C u a 24=。 解 为了解决上述问题,需要了解有关热力学的一些基本规律。例如,热量总是从温度高的物体向温度低的物体传导的;在一定的温度范围内,一个物体的温度变化速度与这一物体的温度和其所在介质温度的差值成正比。这是已为实验证实了的牛顿(Newton )冷却定律。 设物体在时刻t 的温度为)(t u u =,则温度的变化速度以 dt du 来表示。注意到热量总是从温度高的物体向温度低的物体传导的,因而a u u >0。所以温度差a u u -恒正;又因物体将随时间而逐渐冷却,故温度变化速度dt du 恒负。故有: dt du )(a u u k --= (1.1) 这里0>k 是比例常数。方程(1.1)就是物体冷却过程的数学模型,它含有未知函数u 及它的一阶导数dt du ,这样的方程称为一阶微分方程。 为了解出物体的温度u 和时间t 的关系,我们要从方程(1.1)中解出u 。注意到a u 是常数,且0>-a u u ,可将(1.1)改写成 kdt u u u u d a a -=--)( (1.2) 这样u 和t 就被分离开了。两边积分,得到 c kt u u a ~)ln(+-=- (1.3) 这里c ~是任意常数。上式可写成 c kt a e u u ~+-=- 令c e c ~=,则有 kt a ce u u -+= (1.4) 再根据初始条件: 当0=t 时,0u u = (1.5) 可得a u u c -=0,于是 kt a a e u u u u --+=)(0 (1.6) 如果k 的数值确定了,(1.6)就完全决定了温度u 和时间t 的关系。 根据条件10=t 时,1u u =,得到 k a a e u u u u 1001)(--+= 由此得到a a u u u u k --=10ln 101051.066.1ln 10 1≈=。从而 t e u 051.012624-+= (1.7)
数学建模作业求解常微分方程和人口模型问题
实验报告 课程名称:数学建模 课题名称:求解常微分方程与人口模型 专业:信息与计算科学 姓名:胡家炜 班级: 123132 完成日期: 2016 年 6 月 10 日
一.求解微分方程的通解 (1). dsolve('2*x^2*y*Dy=y^2+1','x') ans = (exp(C3 - 1/x) - 1)^(1/2) -(exp(C3 - 1/x) - 1)^(1/2) i -i (2). dsolve('Dy=(y+x)/(y-x)','x') ans = x + 2^(1/2)*(x^2 + C12)^(1/2) x - 2^(1/2)*(x^2 + C12)^(1/2) (3). dsolve('Dy=cos(y/x)+y/x','x') ans = (pi*x)/2-x*log(-(exp(C25 + log(x)) - i) /(exp(C25 + log(x))*i - 1))*i (4). dsolve('(x*cos(y)+sin(2*y))*Dy=1','x') ans = -asin(x/2 + lambertw(0, -(C30*exp(- x/2 - 1))/2) + 1) (5). dsolve('D2y+3*Dy-y=exp(x)*cos(2*x)','x') ans = C32*exp(x*(13^(1/2)/2 - 3/2)) + C33*exp(-x*(13^(1/2)/2 + 3/2)) + (13^(1/2)*exp(x*(13^(1/2)/2-3/2))*exp((5*x)/2(13^(1/2)*x)/2)* (2*sin(2*x) - cos(2*x)*(13^(1/2)/2 - 5/2)))/(13*((13^(1/2)/2 - 5/2)^2 +4))-(13^(1/2)*exp(x*(13^(1/2)/2+3/2))*exp((5*x)/2 +(13^(1/2)*x)/2)*(2*sin(2*x)+cos(2*x)*(13^(1/2)/2+5/2))) /(13*((13^(1/2)/2 + 5/2)^2 + 4)) (6)dsolve('D2y+4*y=x+1+sin(x)','x') ans = cos(2*x)*(cos(2*x)/4 - sin(2*x)/8 + sin(3*x)/12 - sin(x)/4 + (x*cos(2*x))/4 - 1/4) + sin(2*x)*(cos(2*x)/8 - cos(3*x)/12 + sin(2*x)/4 + cos(x)/4 + (x*sin(2*x))/4 + 1/8) + C35*cos(2*x) + C36*sin(2*x)
数学建模实验答案微分方程模型
实验07 微分方程模型(2学时) (第5章 微分方程模型) 1.(验证)传染病模型2(SI 模型)p136~138 传染病模型2(SI 模型): 0(1),(0)di k i i i i dt =-= 其中, i (t )是第t 天病人在总人数中所占的比例。 k 是每个病人每天有效接触的平均人数(日接触率)。 i 0是初始时刻(t =0)病人的比例。 1.1 画~di i dt 曲线图p136~138 取k =0.1,画出i dt di ~的曲线图,求i 为何值时dt di 达到最大值,并在曲线图上标注。 参考程序:
提示:fplot, fminbnd, plot, text, title, xlabel 1)画曲线图 用fplot函数,调用格式如下: fplot(fun,lims) fun必须为一个M文件的函数名或对变量x的可执行字符串。 若lims取[xmin xmax],则x轴被限制在此区间上。 若lims取[xmin xmax ymin ymax],则y轴也被限制。 本题可用 fplot('0.1*x*(1-x)',[0 1.1 0 0.03]); 2)求最大值 用求解边界约束条件下的非线性最小化函数fminbnd,调用格式如下:x=fminbnd('fun',x1,x2) fun必须为一个M文件的函数名或对变量x的可执行字符串。 返回自变量x在区间x1 毕业论文 论文题目:常微分方程在数学建模中的应用姓名: 学科专业: 指导教师: 完成时间: 常微分方程是数学理论(特别是微积分)联系实际的重要工具,它不仅与几何学、力学、电子技术、自动控制、星际航行、甚至和化学、生物学、农业以及经济学都有着密切的联系。本文结合实践背景,建立数学模型,并利用所得结果去解释某些实际问题。 关键字常微分方程、人口预测模型、市场价格模型、混合溶液的数学模型、震动模型 第一章人口预测模型 第二章市场价格模型 第三章混合溶液的数学模型第四章震动模型 绪论 当我们描述实际对象的某些特性随时间(或空间)而演变的过程、分析它的变化规律、预测它的未来性态,研究它的控制手段时,通常要建立对象的动态模型。建模时首先要根据建模目的和对问题的具体分析作出简化假设,然后按照对象在的或可以类比的其他对象的规律列出微分方程,求出方程的解并将结果翻译回实际对象,就可以进行描述、分析、预测或控制了。 事实上在微分方程课程中,解所谓应用题时我们遇到简单的建立动态模型问题,例如“一质量为m的物体自高h处自由下落,初速度是零,设阻力与下落速度的平方成正比,比例系数为k,求下落速度随时间的变化规律。”又如“容器有盐水100L,含盐10kg,令以3L/min的速度从一管放进净水,以2L/min的速度从另一管抽出盐水,设容器盐水浓度始终是均匀的,求容器含盐量随时间变化规律。”本文讨论的是常微分方程在数学建模中的应用。 第一章 人口预测模型 由于资源的有限性,当今世界各国都注意有计划地控制人口的增长,为了得到人口预测模型,必须首先搞清影响人口增长的因素,而影响人口增长的因素很多,如人口的自然出生率、人口的自然死亡率、人口的迁移、自然灾害、战争等诸多因素,如果一开始就把所有因素都考虑进去,则无从下手.因此,先把问题简化,建立比较粗糙的模型,再逐步修改,得到较完善的模型. 例1(马尔萨斯(Malthus )模型) 英国人口统计学家马尔萨斯(1766—1834)在担任牧师期间,查看了教堂100多年人口出生统计资料,发现人口出生率是一个常数,于1789年在《人口原理》一书中提出了闻名于世的马尔萨斯人口模型,他的基本假设是:在人口自然增长过程中,净相对增长(出生率与死亡率之差)是常数,即单位时间人口的增长量与人口成正比,比例系数设为r ,在此假设下,推导并求解人口随时间变化的数学模型. 解 设时刻t 的人口为)(t N ,把)(t N 当作连续、可微函数处理(因人口总数很大,可近似地这样处理,此乃离散变量连续化处理),据马尔萨斯的假设,在t 到t t ?+时间段,人口的增长量为 t t rN t N t t N ?=-?+)()()(, 并设0t t =时刻的人口为0N ,于是 ?????==. ,00)(d d N t N rN t N 这就是马尔萨斯人口模型,用分离变量法易求出其解为 )(00e )(t t r N t N -=, 此式表明人口以指数规律随时间无限增长. 模型检验:据估计1961年地球上的人口总数为91006.3?,而在以后7年中,人口总数以每年2%的速度增长,这样19610=t ,901006.3?=N ,02.0=r ,于是 )1961(02.09e 1006.3)(-?=t t N . 这个公式非常准确地反映了在1700—1961年间世界人口总数.因为,这期间 北方民族大学学士学位论文 论文题目:常微分方程在数学建模中的应用 院(部)名称:信息与计算科学学院 学生姓名:马木沙 专业:信计学号:20093490 指导教师姓名:魏波 论文提交时间: 论文答辩时间: 学位授予时间: 北方民族大学教务处制 摘要 本文利用常微分方程和数学建模二者之间的联系,了解微分方程的一般理论、微分方程解的存在惟一性、微分方程的稳定性问题、通过几个典型的数学模型如:人口模型、减肥的数学模型、化工车间通风模型、传染病的传播模型及定性分析等例子来体现微分方程在数学建模中的应用. 用数学理论解决实际生活中的问题.微分方程的出现以及运用微分方程在数学建模中的应用,就是为了更好地使更多的人理解并运用数学理论,更好的解决实际生活中的问题.努力在各个领域利用并渗透数学知识的广泛运用. 关键词:常微分方程,数学建模,数学模型 Abstract In this paper, ordinary differential equations and mathematical modeling contact between the two, understand the general theory of differential equations, stability problems of the existence and uniqueness of differential equations, differential equations, several typical mathematical models such as: demographic model,example of the mathematical model of weight loss, chemical plant ventilation model, spread of infectious diseases, model and qualitative analysis to reflect the application of differential equations in mathematical modeling. found that the application of mathematical theory to study and solve problems in the actual process of the emergence of ordinary differential equations andOrdinary Differential Equations in Mathematical Modeling widely used, in order to better enable ordinary people to understand and use mathematical theory, solving real-world problems. sublimation theory by the knowledge-based transformation to the ability to type, highlight the differential equationsand differential equations in mathematical modeling efforts made outstanding and significant contribution in various fields. Keywords: ordinary differential equations, mathematical modeling, mathematical model. 第七节 扩散问题的偏微分方程模型 物质的扩散问题,在石油开采、环境污染、疾病流行、化学反应、新闻传播、煤矿瓦斯爆炸、农田墒情、水利工程、生态问题、房屋基建、神经传导、药物在人体内分布以及超导、液晶、燃烧等诸多自然科学与工程技术领域,十分普遍地存在着. 显然,对这些问题的研究是十分必要的,其中的数学含量极大. 事实上,凡与反应扩散有关的现象,大都能由线性或非线性抛物型偏微分方程作为数学模型来定量或定性地加以解决. MCM的试题来自实际,是“真问题⊕数学建模⊕计算机处理”的“三合一”准科研性质的一种竞赛,对上述这种有普遍意义和数学含量高,必须用计算机处理才能得到数值解的扩散问题,当然成为试题的重要来源,例如,AMCM-90A,就是这类试题;AMCM-90A要研究治疗帕金森症的多巴胺(dopamine )在人脑中的分布,此药液注射后在脑子里经历的是扩散衰减过程,可以由线性抛物型方程这一数学模型来刻划. AMCM-90A要研究单层住宅混凝土地板中的温度变化,也属扩散(热传导)问题,其数学模型与AMCM-90A一样,也是线性抛物型方程. 本文交代扩散问题建模的思路以及如何推导出相应的抛物型方程,如何利用积分变换求解、如何确定方程与解的表达式中的参数等关键数学过程,且以AMCM-90A题为例,显示一个较细致的分析、建模、求解过程. §1 抛物型方程的导出 设(,,,)u x y z t 是t 时刻点(,,)x y z 处一种物质的浓度. 任取一个闭曲面S ,它所围的区域是Ω,由于扩散,从t 到t t +?时刻这段时间内,通过S 流入Ω的质量为 2 221(cos cos cos )dSd t t t S u u u M a b c t x y z αβγ+????=++???? ??. 由高斯公式得 2222 221222()d d d d t t t u u u M a b c x y z t x y z +?Ω ???=++???? ???. (1) 其中,222,,a b c 分别是沿,,x y z 方向的扩散系数. 由于衰减(例如吸收、代谢等),Ω内的质量减少为 2 2d d d d t t t M k u x y z t +?Ω =? ???, (2) 其中2 k 是衰减系数. 由物质不灭定律,在Ω内由于扩散与衰减的合作用,积存于Ω内的质量为12M M -. 换一种角度看,Ω内由于深度之变化引起的质量增加为 3[(,,,)(,,,)]d d d d d d d . (3)t t t M u x y z t t u x y z t x y z u x y z t t Ω +?Ω =+?-?=????? ??? 显然312M M M =-,即 数学模型 13.人体注射葡萄糖溶液时,血液中葡萄糖浓度g(t)的增长率与注射速率r 成正比,与人体血液容积v 成反比,而由于人体组织的吸收作用,g(t)的减少率与g(t)本身成正比。分别在以下几种假设下建立模型,并讨论稳定情况。 (1)人体血液容积v 不变。 (2)v 随着注入溶液而增加。 (3)由于排泄等因素v 的 增加有极限值 解:模型假设: 本模型中主要符号说明为: 葡萄糖浓度g(t) 注射速率r 人体血液容积v 基本模型为: g k V r k dt dg 21-= (1k ,02>k ,常数) ⑴ (1)V 为常数时,平衡点V k r k g 210= 稳定。 如果以g 为横轴、 dt dg 为纵轴作出方程的图形(图1),可以分析葡萄糖浓度增长速度dt dg 随着g 的增加而变化的情况,从而大概地看出g(t)的变化规律。 令2.01=k ,5.02=k ,利用Mathematica 在操作窗口中输入以下代码命令: Plot[0.2/100-0.5g,{g,0,100},PlotStyle->{RGBColor[1,0,0]}] 得到: 图1 dt dg ~g 曲线 再利用matlab 在操作窗口中输入以下代码命令: g=dsolve('Dg=k1*r/v-k2*g','g(0)=g0','t') 其解为 g =k1*r/v/k2+exp(-k2*t)*(-k1*r+g0*v*k2)/v/k2 整理得到: 2 20112)(vk vk g r k e v r k t g t k +-+=- ⑵ 令2.01=k ,5.02=k ,利用Mathematica 在操作窗口中输入以下代码命令: Plot[0.2/100+Exp[-0.5t],{t,0,100},PlotStyle->{RGBColor[1,0,0]}] 得到: 图2 g ~t 曲线 由图可以知道它在平衡点V k r k g 210= 稳定。 (2)不妨设 β=dt dV (0>β,常数) ⑶ 方程⑴,⑵不存在平衡点。若由⑵解出t V t V β+=0)(代入⑴,得到 g k t V r k dt dg 201-+=β ⑷ 则⑷不能是自治方程。因为平衡点及稳定性的概念只是对自治方程而言才有意义,而⑷不能是自治方程,所以不能考虑它的稳定性。 (3)不妨设 V )(V dt dV -=1μ (0>μ,常数) ⑸ 如果以V 为横轴、dt dV 为纵轴作出方程的图形(图3),可以分析人体血液容积V 增长速度dt dV 随着V 的增加而变化的情况,从而大概地看出V(t)的变化规 第八节 数学建模——微分方程的应用举例 微分方程在物理学、力学、经济学和管理科学等实际问题中具有广泛的应用,本节我们将集中讨论微分方程的实际应用,尤其是微分方程经济学中的应用. 读者可从中感受到应用数学建模的理论和方法解决实际问题的魅力. 内容分布图示 ★衰变问题 ★逻辑斯谛方程 ★价格调整问题 ★人才分配问题模型 ★追迹问题 ★返回 内容要点: 一、衰变问题 镭、铀等放射性元素因不断放射出各种射线而逐渐减少其质量, 这种现象称为放射性物质的衰变. 根据实验得知, 衰变速度与现存物质的质量成正比, 求放射性元素在时刻t 的质量. 用x 表示该放射性物质在时刻t 的质量, 则dt dx 表示x 在时刻t 的衰变速度, 于是“衰变速度与现存的质量成正比”可表示为 .kx dt dx -= (8.1) 这是一个以x 为未知函数的一阶方程, 它就是放射性元素衰变的数学模型, 其中0>k 是比例常数, 称为衰变常数, 因元素的不同而异. 方程右端的负号表示当时间t 增加时, 质量x 减少. 解方程(8.1)得通解.kt Ce x -=若已知当0t t =时, ,0x x =代入通解kt Ce x -=中可得 ,00kt e x C -= 则可得到方程(8.1)特解 ,)(00t t k e x x --= 它反映了某种放射性元素衰变的规律. 注: 物理学中, 我们称放射性物质从最初的质量到衰变为该质量自身的一半所花费的时间为半衰期, 不同物质的半衰期差别极大. 如铀的普通同位素(U 238 )的半衰期约为50亿年; 通常的镭(Ra 226 )的半衰期是上述放射性物质的特征, 然而半衰期却不依赖于该物质的初始 量, 一克 Ra 226 衰变成半克所需要的时间与一吨Ra 226衰变成半吨所需要的时间同样都是 1600年, 正是这种事实才构成了确定考古发现日期时使用的著名的碳-14测验的基础. 二、 逻辑斯谛方程: 逻辑斯谛方程是一种在许多领域有着广泛应用的数学模型, 下面我们借助树的增长来建立该模型. 一棵小树刚栽下去的时候长得比较慢, 渐渐地, 小树长高了而且长得越来越快, 几年不见, 绿荫底下已经可乘凉了; 但长到某一高度后, 它的生长速度趋于稳定, 然后再慢慢降下 第八节数学建模——微分方程的应用举例 微分方程在物理学、力学、经济学和管理科学等实际问题中具有广泛的应用,本节我们将集中讨论微分方程的实际应用,读者可从中感受到应用数学建模的理论和方法解决实际问题的魅力. 内容分布 ★衰变问题 ★逻辑斯谛方程 ★价格调整问题 ★人才分配问题模型 ★追迹问题 内容要点: 一、衰变问题 镭、铀等放射性元素因不断放射出各种射线而逐渐减少其质量, 这种现象称为放射性物质的衰变. 根据实验得知, 衰变速度与现存物质的质量成正比, 求放射性元素在时刻t的质量. 用x表示该放射性物质在时刻t的质量, 则 表示x在时刻t的衰变速度, 于是“衰变速度与现存的质量成正比”可表示为 (8.1) 这是一个以x为未知函数的一阶方程, 它就是放射性元素衰变的数学模型, 其中 是比例常数, 称为衰变常数, 因元素的不同而异. 方程右端的负号表示当时间t增加时, 质量x减少. 解方程(8.1)得通解 若已知当 时, 代入通解 中可得 则可得到方程(8.1)特解 它反映了某种放射性元素衰变的规律. 注: 物理学中, 我们称放射性物质从最初的质量到衰变为该质量自身的一半所花费的时间为半衰期, 不同物质的半衰期差别极大. 如铀的普通同位素( )的半衰期约为50亿年;通常的镭( )的半衰期是1600年.半衰期是上述放射性物质的特征, 然而半衰期却不依赖于该物质的初始量, 一克 衰变成半克所需要的时间与一吨 衰变成半吨所需要的时间同样都是1600年, 正是这种事实才构成了确定考古发现日期时使用的著名的碳-14测验的基础. 二、逻辑斯谛(Logistic)方程: 逻辑斯谛方程是一种在许多领域有着广泛应用的数学模型, 下面我们借助树的增长来建立该模型. 一棵小树刚栽下去的时候长得比较慢, 渐渐地, 小树长高了而且长得越来越快, 几年不见, 绿荫底下已经可乘凉了; 但长到某一高度后, 它的生长速度趋于稳定, 然后再慢慢降下来. 这一现象很具有普遍性. 现在我们来建立这种现象的数学模型. 如果假设树的生长速度与它目前的高度成正比, 则显然不符合两头尤其是后期的生长情形, 因为树不可能越长越快; 但如果假设树的生长速度正比于最大高度与目前高度的差, 则又明显不符合中间一段的生长过程. 折衷一下, 我们假定它的生长速度既与目前的高度,又与最大高度与目前高度之差成正比. 设树生长的最大高度为H(m), 在t(年)时的高度为h(t), 则有 (8.2) 其中 是比例常数. 这个方程为Logistic方程. 它是可分离变量的一阶常数微分方程. 下面来求解方程(8.2). 分离变量得 两边积分 得 实验一SDH网元基本配置 一、实验目的: 通过本实验,了解SDH光传输的原理和系统组成,了解ZXMP S325设备的硬件构成和单板功能,学习ZXONM 300 网管软件的使用方法,掌握SDH 网元配置的基本操作。 二、实验器材: 1、SDH 设备:3 套ZXMP 325; 2、实验用维护终端。 三、实验原理 1、SDH 原理 同步数字体制(SDH)是为高速同步通信网络制定的一个国际标准,其基础在于直接同步复用。按照SDH 组建的网络是一个高度统一的、标准化的、智能化的网络,采用全球统一的接口以实现多环境的兼容,管理操作协调一致,组网与业务调度灵活方便,并且具有网络自愈功能,能够传输所有常见的支路信号,应用于多种领域(如光纤传输,微波和卫星传输等)。 SDH 具有以下特点: (1)接口:接口的规范化是设备互联的关键。SDH对网络节点接口(NNI)作了统一的规范,内容包括数字信号数率等级、帧结构、复接方法、线路接口、监控管理等。 电接口:STM-1是SDH的第一个等级,又叫基本同步传送模块,比特率为155.520Mb/s;STM-N是SDH第N个等级的同步传送模块,比特率是STM-1的N 倍(N=4n=1,4,16,- - -)。 光接口:采用国际统一标准规范。SDH仅对电信号扰码,光口信号码型是加扰的NRZ 码,信号数率与SDH 电口标准信号数率相一致。 (2)复用方式 a)低速SDH----高速SDH,字节间插; b) 低速PDH-----SDH,同步复用和灵活的映射。 (3)运行维护:用于运行维护(OAM)的开销多,OAM功能强——这也是线路编码不用加冗余的原因. (4)兼容性:SDH 具有很强的兼容性,可传送PDH 业务,异步转移模式信号(ATM)及其他体制的信号。 (5)SDH 复用映射示意图 常微分方程在数学建模中的应用 摘要: 正文: 数学建模概述 建模定义: 数学建模(Mathematical Modeling)就是通过计算得到的结果来解释实际问题,并接受实际的检验,来建立数学模型的全过程。数学模型(Mathematical Model)是一种模拟,是用数学符号,数学式子,程序,图形等对实际课题本质属性的抽象而又简洁的刻画,它或能解释某些客观现象,或能预测未来的发展规律,或能为控制某一现象的发展提供某种意义下的最优策略或较好策略。数学模型一般并非现实问题的直接翻版,它的建立常常既需要人们对现实问题深入细微的观察和分析,又需要人们灵活巧妙地利用各种数学知识。这种应用知识从实际课题中抽象、提炼出数学模型的过程就称为数学建模。 建模步骤: 1.模型准备 在解决一个问题之前,我们首先要弄清楚这个问题的具体含义,包含的数学关系。需要求解的问题,限制条件和里面的逻辑关系。用数学语言将这个问题进行翻译。同时,要在图书馆或网上资料库找到相关文章,或数据支持。加深自己对这个问题的理解的同时,也为下文的求解提供一定的理论支持和参考。 2.模型假设 实际生活中的问题非常复杂,相关影响因素也特别多,我们不可能把所有的因素都考虑在内,往往需要通过假设忽略其中一些不重要、对结果影响小、发生几率不大、符合常识的假设。通过这些假设对问题进行简化。 3.模型建立 建立模型的过程就是对问题进行数学语言转化的过程,其中要注意模型尽可能地简单,不能太复杂,所运用的数学原理要适用于该问题。而且尽可能转化成自己熟悉的,擅长的模型。 4.模型求解 模型的求解往往要运用合适的数学软件,如SPSS,MATLAB,R,Lingo,Python 等。根据自己的问题的不同类型选择合适的软件进行求解。结果可能呈现出数据,图表,分析表等不同的形式。 5.模型检验 进行模型检验时,通常通过利用已知过给数据和所给的一个相应结果检验模型的正确性。如图像重建;预测模型可以通过以往数据进行检验;相关性问题通过R 值进行检验等。通过检验说明该模型精度高,反之可能是模型本身的不足或数据计算错误。要重新修订或优化模型。 数学建模中能用的方法很多,根据不同问题的特性选择合适的方法,建立合适的模型。但是常微分方程这种数学方法在很多问题中都有应用,在此我们选取两个最典型的运用常微分方程的模型——Logistic人口模型和传染病模型,来加以简单的说明。 常微分方程模型:常微分方程在数学建模中的应用论文正稿
常微分方程在数学建模中的应用
扩散问题的偏微分方程模型,数学建模
数学模型 微 分 方 程
数学建模微分方程的应用举例
数学建模微分方程的应用举例
扩散问题的偏微分方程模型_数学建模
常微分方程在数学建模中的应用
