数学提高题专题复习平行四边形练习题含答案

数学提高题专题复习平行四边形练习题含答案

一、解答题

1．如图，在Rt ABC 中，90ACB ∠=?，过点C 的直线//MN AB ，D 为AB 边上一

点，过点D 作DE BC ⊥，交直线MN 于E ，垂足为F ，连接CD 、BE

（1）当D 在AB 中点时，四边形BECD 是什么特殊四边形?说明你的理由； （2）当D 为AB 中点时，A ∠等于 度时，四边形BECD 是正方形． 2．如图正方形ABCD ，DE 与HG 相交于点O （O 不与D 、E 重合）．

（1）如图（1），当90GOD ∠=?， ①求证：DE GH =； ②求证：2GD EH DE +>

；

（2）如图（2），当45GOD ∠=?，边长4AB =，5HG =，求DE 的长． 3．如图，正方形ABCO 的边OA 、OC 在坐标轴上，点B 坐标为（6，6），将正方形ABCO 绕点C 逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF ，ED 交线段AB 于点G ，ED 的延长线交线段OA 于点H ，连结CH 、CG ． （1）求证：CG 平分∠DCB ；

（2）在正方形ABCO 绕点C 逆时针旋转的过程中，求线段HG 、OH 、BG 之间的数量关系； （3）连结BD 、DA 、AE 、EB ，在旋转的过程中，四边形AEBD 是否能在点G 满足一定的条件下成为矩形？若能，试求出直线DE 的解析式；若不能，请说明理由．

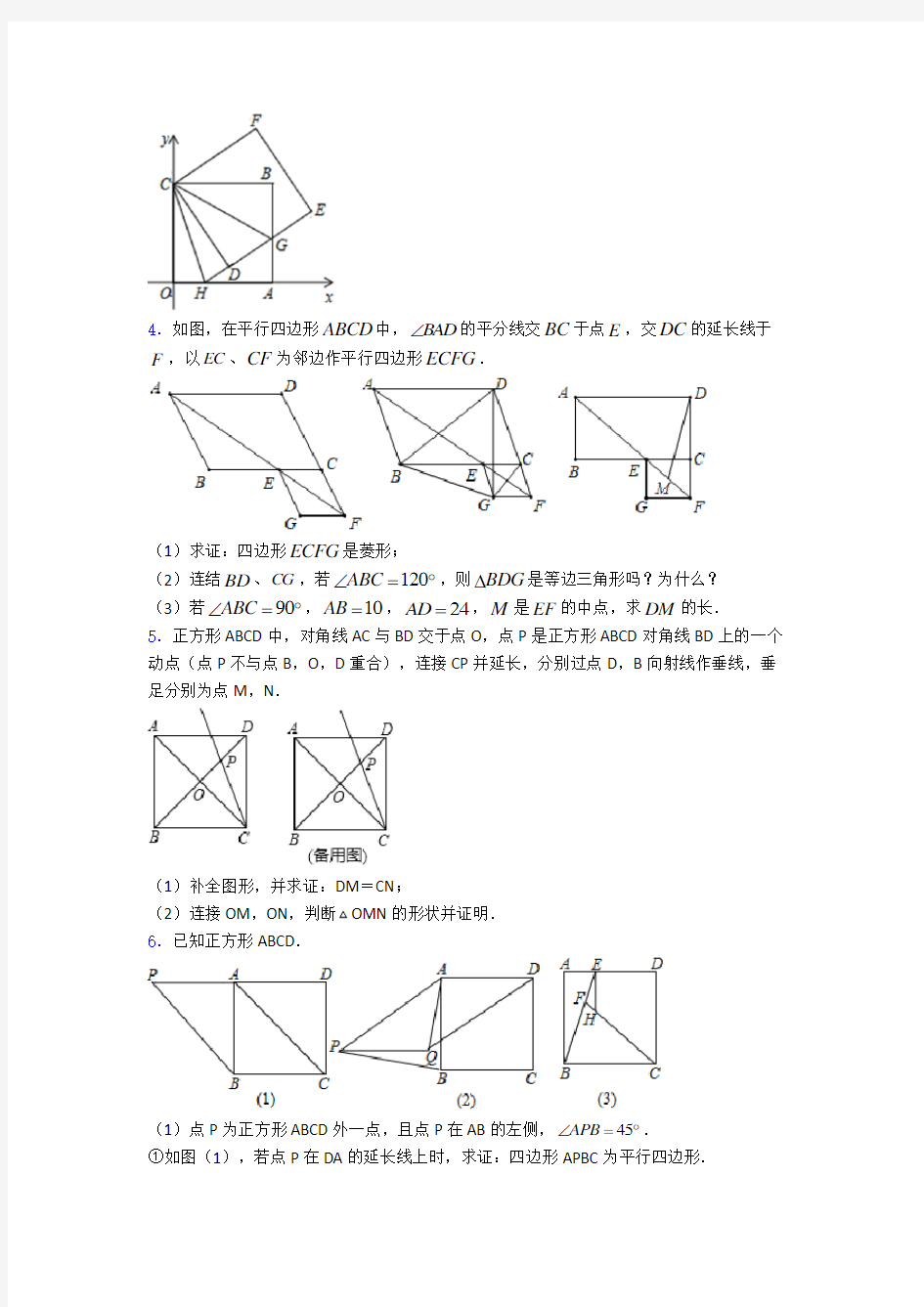
4．如图，在平行四边形ABCD 中，BAD ∠的平分线交BC 于点E ，交DC 的延长线于

F ，以EC 、CF 为邻边作平行四边形ECF

G ．

（1）求证：四边形ECFG 是菱形；

（2）连结BD 、CG ，若120ABC ∠=?，则BDG ?是等边三角形吗？为什么？ （3）若90ABC ∠=?，10AB =，24AD =，M 是EF 的中点，求DM 的长． 5．正方形ABCD 中，对角线AC 与BD 交于点O ，点P 是正方形ABCD 对角线BD 上的一个动点（点P 不与点B ，O ，D 重合），连接CP 并延长，分别过点D ，B 向射线作垂线，垂足分别为点M ，N ．

（1）补全图形，并求证：DM ＝CN ；

（2）连接OM ，ON ，判断OMN 的形状并证明． 6．已知正方形ABCD ．

（1）点P 为正方形ABCD 外一点，且点P 在AB 的左侧，45APB ∠=?． ①如图（1），若点P 在DA 的延长线上时，求证：四边形APBC 为平行四边形．

②如图（2），若点P 在直线AD 和BC 之间，以AP ，AD 为邻边作APQD □，连结AQ ．求∠PAQ 的度数．

（2）如图（3），点F 在正方形ABCD 内且满足BC=CF ，连接BF 并延长交AD 边于点E ，过点E 作EH ⊥AD 交CF 于点H ，若EH=3，FH=1，当1

3

AE CF =时．请直接写出HC 的长________．

7．如图，在正方形ABCD 中，E 是边AB 上的一动点（不与点A 、B 重合），连接

DE ，点A 关于直线DE 的对称点为F ，连接EF 并延长交BC 于点G ，连接DG ，过点E 作EH DE ⊥交DG 的延长线于点H ，连接BH ．

（1）求证：GF GC =；

（2）用等式表示线段BH 与AE 的数量关系，并证明．

8．已知在ABC 和ADE 中， 180ACB AED ∠+∠=?，CA CB =，EA ED =，3AB =．

（1）如图1，若90ACB ∠=?，B 、A 、D 三点共线，连接CE ： ①若52

2

CE =

，求BD 长度； ②如图2，若点F 是BD 中点，连接CF ，EF ，求证：2CE EF =；

（2）如图3，若点D 在线段BC 上，且2CAB EAD ∠=∠，试直接写出AED 面积的最

小值．

9．如图①，已知正方形ABCD的边长为3，点Q是AD边上的一个动点，点A关于直线BQ的对称点是点P，连接QP、DP、CP、BP，设AQ=x．

（1）BP＋DP的最小值是_______，此时x的值是_______；

（2）如图②，若QP的延长线交CD边于点M，并且∠CPD=90°．

①求证：点M是CD的中点；②求x的值．

（3）若点Q是射线AD上的一个动点，请直接写出当△CDP为等腰三角形时x的值．

10．定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径。

（1）如图1，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段AC，同时我们还发现损矩形中有公共边的两个三角形角的特点，在公共边的同侧的两个角是相等的。如图1中：△ABC和△ABD有公共边AB，在AB同侧有∠ADB和∠ACB，此时∠ADB＝

∠ACB；再比如△ABC和△BCD有公共边BC，在CB同侧有∠BAC和∠BDC，此时∠BAC＝∠BDC。请再找一对这样的角来＝

（2）如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF 的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由。

（3）在第（2）题的条件下，若此时AB＝3，BD＝42，求BC的长。

【参考答案】***试卷处理标记，请不要删除

一、解答题

1．（1）四边形BECD 是菱形，理由见解析；（2）45? 【分析】

（1）先证明//AC DE ，得出四边形BECD 是平行四边形，再“根据直角三角形斜边上的中线等于斜边的一半”证出CD BD =，得出四边形BECD 是菱形；

（2）先求出45ABC ∠=?，再根据菱形的性质求出90DBE ∠=?，即可证出结论． 【详解】

解：当点D 是AB 的中点时，四边形BECD 是菱形；理由如下： ∵DE BC ⊥，

90DFE ∴∠=?，

∵90ACB ∠=?，

ACB DFB ∴∠=∠， //AC DE ∴，

∵//MN AB ，即//CE AD ， ∴四边形ADEC 是平行四边形， CE AD ∴=； D 为AB 中点， AD BD ∴=， BD CE ∴=， ∵//BD CE ，

∴四边形BECD 是平行四边形， ∵90ACB ∠=?，D 为AB 中点，

1

2

CD AB BD ∴==，

∴四边形BECD 是菱形；

（2）当45A ∠=?时，四边形BECD 是正方形；理由如下： ∵90ACB ∠=?，45A ∠=?， 45ABC ∴∠=?，

∵四边形BECD 是菱形，

1

2

ABC DBE ∴∠=∠，

90DBE ∴∠=?，

∴四边形BECD 是正方形． 故答案为：45?． 【点睛】

本题考查了平行四边形的判定、正方形的判定以及直角三角形的性质；根据题意证明线段相等和直角是解决问题的关键．

2．（1）①证明见解析；②证明见解析；（2

）3

DE =． 【分析】

（1）过点D 作//DM GH 交BC 延长线于点M ，连接EH ，

①由正方形的性质可得//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=?，即可证明四边形DGHM 是平行四边形，可得DM=GH ，由90GOD ∠=?可得∠EDM=90°，根据直角三角形两锐角互余的性质可得12∠=∠，利用ASA 可证明△ADE≌△CDM，可得DE=DM ，即可证明DE=GH ；

②由①得DM=DE ，根据勾股定理可得

，利用三角形三边关系即可得结论； （2）过点D 作DN//GH 交BC 于点N ，作ADM CDN ∠=∠，DM 交BA 延长线于点

M ，可证明四边形GHND 为平行四边形，可得DN HG =，GD HN =，根据勾股定理可求出CN 的长，利用AAS 可证明ADM CDN ??≌，可得AM NC =，DM DN =，根据

平行线的性质∠EDN=45°，根据角的和差故选可得∠MDE=∠EDN ，利用SAS 可证明

MDE NDE ??≌，即可证明AE CN EN +=，设AE x =，利用勾股定理可求出x 的值，进而利用勾股定理求出DE 的值即可得答案． 【详解】

（1）如图（1），过点D 作//DM GH 交BC 延长线于点M ，连接EH ，EM ， ①∵四边形ABCD 为正方形，

∴//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=? ∴四边形DGHM 为平行四边形， ∴DM=GH ，GD HM =， ∵90GOD ∠=?，

∴90EDM EOH ∠=∠=?， ∴290EDC ∠+∠=?， ∵90ADC ∠=?， ∴190EDC ∠+∠=?， ∴12∠=∠，

在ADE ?和CDM ?中12A DCM AD DC ∠=∠??

=??∠=∠?

，

∴ADE CDM ??≌， ∴DE DM =， ∴DE GH =．

②在DEM ?中，∠EDM=90°， ∴222DE DM EM +=， ∵DE DM =， ∴222DE EM =， ∴2EM DE =

，

在EHM ?中，HM EH EM +>， ∵GD HM =， ∴2GD EH GH +≥

．

（2）如图（2），过点D 作DN//GH 交BC 于点N ，则四边形GHND 为平行四边形， ∴DN HG =，GD HN =，

∵90C ∠=?，4CD AB ==，25HG DN == ∴222CN DN DC =

-=，

∴422BN BC CN =-=-=，

作ADM CDN ∠=∠，DM 交BA 延长线于点M ，

在ADM ?和CDN ?中90C MAD CDN ADM DC AD ∠=∠=???

∠=∠??=?

，

∴ADM CDN ??≌， ∴AM NC =，DM DN =， ∵45GOD EOH ∠=∠=?， ∴45EDN ∠=?， ∴45ADE CDN ∠+∠=?， ∴45ADE ADN MDE ∠+∠=?=∠，

在MDE ?和NDE ?中MD ND MDE EDN DE DE =??

∠=∠??=?

，

∴MDE NDE ??≌，

∴EM EN =，即AE AM AE CN EN +=+=，

设AE x =，则BE=4-x ，

在Rt BEN ?中，2

2

2

2(2)x x +=+， 解得：43

x =

， ∴2

2

2

2

441043DE AD AE ??=+=+= ???

．

【点睛】

本题考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、三角形的三边关系及勾股定理，熟练掌握相关性质及判定定理，并正确作出辅助线是解题关键． 3．（1）见解析；（2） HG ＝OH +BG ；（3）能成矩形，y 33

42

x =-． 【分析】

（1）根据旋转和正方形的性质可得出CD ＝CB ，∠CDG ＝∠CBG ＝90，根据全等直角三角形的判定定理（HL ）即可证出Rt △CDG ≌Rt △CBG ，即∠DCG ＝∠BCG ，由此即可得出CG 平分∠DCB ；

（2）由（1）的Rt △CDG ≌Rt △CBG 可得出BG ＝DG ，根据全等直角三角形的判定定理（HL ）即可证出Rt △CHO ≌Rt △CHD ，即OH ＝HD ，再根据线段间的关系即可得出HG ＝HD +DG ＝OH +BG ；

（3）根据（2）的结论即可找出当G 点为AB 中点时，四边形AEBD 为矩形，再根据正方形的性质以及点B 的坐标可得出点G 的坐标，设H 点的坐标为（x ，0），由此可得出HO ＝x ，根据勾股定理即可求出x 的值，即可得出点H 的坐标，结合点H 、G 的坐标利用待定系数法即可求出直线DE 的解析式． 【详解】

（1）∵正方形ABCO 绕点C 旋转得到正方形CDEF ，∴CD ＝CB ，∠CDG ＝∠CBG ＝90°．在Rt △CDG 和Rt △CBG 中，∵CG CG

CD CB

=??

=?，∴Rt △CDG ≌Rt △CBG （HL ），∴∠DCG ＝∠BCG ，即CG 平分∠DCB ．

（2）由（1）证得：Rt △CDG ≌Rt △CBG ，∴BG ＝DG ．在Rt △CHO 和Rt △CHD 中，

∵

CH CH

CO CD

=

?

?

=

?

，∴Rt△CHO≌Rt△CHD（HL），∴OH＝HD，∴HG＝HD+DG＝OH+BG．

（3）假设四边形AEBD可为矩形．

当G点为AB中点时，四边形AEBD为矩形，如图所示．

∵G点为AB中点，∴BG＝GA1

2

=AB，由（2）证得：

BG＝DG，则

BG＝GA＝DG

1

2

=AB

1

2

=DE＝GE，又AB＝DE，∴四边形AEBD为矩

形，∴AG＝EG＝BG＝DG．

∵AG1

2

=AB＝3，∴G点的坐标为（6，3）．

设H点的坐标为（x，0），则HO＝x，∴HD＝x，DG＝3．

在Rt△HGA中，HG＝x+3，GA＝3，HA＝6﹣x，由勾股定理得：（x+3）2＝32+（6﹣x）2，解得：x＝2，∴H点的坐标为（2，0）．

设直线DE的解析式为：y＝kx+b（k≠0），将点H（2，0）、G（6，3）代入y＝kx+b中，

得：

20

63

k b

k b

+=

?

?

+=

?

，解得：

3

4

3

2

k

b

?

=

??

?

?=-

??

，∴直线DE的解析式为：y33

42

x

=-．

故四边形AEBD能为矩形，此时直线DE的解析式为：y

33 42

x

=-．

【点睛】

本题考查了矩形的性质、旋转的性质、全等三角形的判定及性质、待定系数法求函数解析式以及勾股定理．解题的关键是：（1）证出Rt△CDG≌Rt△CBG；（2）找出

BG＝DG、OH＝HD；（3）求出点H、G的坐标．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边和角是关键．

4．（1）详见解析；（2）是，详见解析；（3）132

【分析】

（1）平行四边形的性质可得AD∥BC，AB∥CD，再根据平行线的性质证明∠CEF=∠CFE，根据等角对等边可得CE=CF，再有条件四边形ECFG是平行四边形，可得四边形ECFG为菱形，即可解决问题；

（2）先判断出∠BEG=120°=∠DCG，再判断出AB=BE，进而得出BE=CD，即可判断出

△BEG≌△DCG（SAS），再判断出∠CGE=60°，进而得出△BDG是等边三角形，即可得出结论；

（3）首先证明四边形ECFG为正方形，再证明△BME≌△DMC可得DM=BM，

∠DMC=∠BME，再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形，由等腰直角三角形的性质即可得到结论．

【详解】

（1）证明：

∵AF平分∠BAD，

∴∠BAF=∠DAF，

∵四边形ABCD是平行四边形，

∴AD∥BC，AB∥CD，

∴∠DAF=∠CEF，∠BAF=∠CFE，

∴∠CEF=∠CFE，

∴CE=CF，

又∵四边形ECFG是平行四边形，

∴四边形ECFG为菱形；

（2）∵四边形ABCD是平行四边形，

∴AB∥DC，AB=DC，AD∥BC，

∵∠ABC=120°，

∴∠BCD=60°，∠BCF=120°

由（1）知，四边形CEGF是菱形，

∴CE=GE，∠BCG=1

2

∠BCF=60°，

∴CG=GE=CE，∠DCG=120°，∵EG∥DF，

∴∠BEG=120°=∠DCG，

∵AE是∠BAD的平分线，∴∠DAE=∠BAE，

∵AD∥BC，

∴∠DAE=∠AEB，

∴∠BAE=∠AEB，

∴AB=BE，

∴BE=CD，

∴△BEG≌△DCG（SAS），∴BG=DG，∠BGE=∠DGC，∴∠BGD=∠CGE，

∵CG=GE=CE，

∴△CEG是等边三角形，

∴∠CGE=60°，

∴∠BGD=60°，

∵BG=DG，

∴△BDG是等边三角形；

（3）如图2中，连接BM，MC，

∵∠ABC=90°，四边形ABCD是平行四边形，∴四边形ABCD是矩形，

又由（1）可知四边形ECFG为菱形，

∠ECF=90°，

∴四边形ECFG为正方形．

∵∠BAF=∠DAF，

∴BE=AB=DC，

∵M为EF中点，

∴∠CEM=∠ECM=45°，

∴∠BEM=∠DCM=135°，

在△BME和△DMC中，

∵

BE CD

BEM DCM EM CM

=

?

?

∠=∠

?

?=

?

，

∴△BME≌△DMC（SAS），

∴MB=MD，

∠DMC=∠BME．

∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°，∴△BMD是等腰直角三角形．

∵AB=10，AD=24，

∴2222

1024

AB AD

++=26，

∴

2

132 DM BD

==

【点睛】

本题主要考查了平行四边形的判定与性质，全等三角形的判定与性质，等边三角形的判定与性质，菱形的判定与性质，正方形的判定与性质，等腰直角三角形的判定和性质等知识点，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．

5．（1）见解析；（2）MON 为等腰直角三角形，见解析 【分析】

（1）如图1，由正方形的性质得CB ＝CD ，∠BCD ＝90°，再证明∠BCN ＝∠CDM ，然后根据“AAS”证明△CDM ≌△CBN ，从而得到DM ＝CN ；

（2）如图2，利用正方形的性质得OD ＝OC ，∠ODC ＝∠OCB ＝45°，∠DOC ＝90°，再利用∠BCN ＝∠CDM 得到∠OCN ＝∠ODM ，则根据“SAS”可判断△OCN ≌△ODM ，从而得到ON ＝OM ，∠CON ＝∠DOM ，所以∠MON ＝∠DOC ＝90°，于是可判断△MON 为等腰直角三角形． 【详解】

（1）证明：如图1， ∵四边形ABCD 为正方形， ∴CB ＝CD ，∠BCD ＝90°， ∵DM ⊥CP ，BN ⊥CP ， ∴∠DMC ＝90°，∠BNC ＝90°，

∵∠CDM+∠DCM ＝90°，∠BCN+∠DCM ＝90°， ∴∠BCN ＝∠CDM ， 在△CDM 和△CBN 中

DMC CNB CD CB

CDM BCN ∠=∠??

=??∠=∠?

， ∴△CDM ≌△CBN ， ∴DM ＝CN ；

（2）解：△OMN 为等腰直角三角形． 理由如下：

如图2，∵四边形ABCD 为正方形，

∴OD ＝OC ，∠ODC ＝∠OCB ＝45°，∠DOC ＝90°， ∵∠BCN ＝∠CDM ，

∴∠BCN ﹣45°＝∠CDM ﹣45°，即∠OCN ＝∠ODM ， 在△OCN 和△ODM 中

CN DM OCN ODM OC OD =??

∠=∠??=?

， ∴△OCN ≌△ODM ，

∴ON ＝OM ，∠CON ＝∠DOM ， ∴∠MON ＝∠DOC ＝90°， ∴MON 为等腰直角三角形．

【点睛】

本题考查正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质；两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．也考查全等三角形的判定与性质． 6．（1）①证明见详解；②45PAQ ∠=?，见解析；（2）5． 【分析】

（1）①只要证明//PB AC 即可解决问题；②如图2中，连接QC ，作DT DQ ⊥交QC 的延长线于T ，利用全等三角形的性质解决问题即可；

（2）如图3中，延长EH 交BC 于点G ，设AE=x ，由题意易得AB=BC=CF=EG=3x ，然后可得CG=2x ，HG=3x-3，CH=3x-1，利用勾股定理求解即可． 【详解】

（1）①证明：

四边形ABCD 是正方形，∴//B DP C ，45DAC ∠=?，∴135PAC ∠=? 45APB ∠=?，∴+180APB PAC ∠∠=?，∴//PB AC

∴四边形APBC 是平行四边形；

②

四边形PADQ 是平行四边形，∴DQ//,//,AP AD PQ AD PQ BC ==，

AD//B C ，∴,//PQ BC PQ BC =，∴四边形PQCB 是平行四边形，

∴QC//BP ，∴45APQ DQC ∠=∠=?，90ADC QDT ∠=∠=?，

∴DQ=DT ，45,T DQT ADQ CDT ∠=∠=?∠=∠，

AD=DC ，∴ADQ CDT ≌，∴45AQD T ∠=∠=?， AP//DQ ，∴45PAQ DQA ∠=∠=?；

（3）CH=5，理由如下：

如图3所示：延长EH 交BC 于点G ；

四边形ABCD 是正方形，∴AB=BC ，90D ∠=?， 又

EH=3，FH=1，EH ⊥AD ，∴EH//CD ，∴90HGC ∠=?

设AE=x ，

1

,3

AE CF BC CF ==，∴AB=BC=CF=EG=3x ， ∴CG=2x ，HG=3x-3，CH=3x-1

在Rt HGC △中，()()2

2

2222

43331CG HG CH x x x +=+-=-即，解得121,2x x ==

当x=1时，AB=3(不符合题意，舍去)； 当x=2时，AB=6，∴CH=5． 故答案为5． 【点睛】

本题主要考查正方形的综合问题、三角形全等及勾股定理，关键是利用已知条件及四边形的性质得到它们之间的联系，然后利用勾股定理求解线段的长即可． 7．（1）详见解析；（2）2BH AE ，理由详见解析 【分析】

1）如图1，连接DF ，根据对称得：△ADE ≌△FDE ，再由HL 证明Rt △DFG ≌Rt △DCG ，可得结论；

（2）如图2，作辅助线，构建AM=AE ，先证明∠EDG=45°，得DE=EH ，证明△DME ≌△EBH ，则EM=BH ，根据等腰直角△AEM 得：2EM AE =，得结论；

【详解】

证明：（1）如图1，连接DF ，

∵四边形ABCD 是正方形， ∴DA DC =，90A C ∠=∠=?， ∵点A 关于直线DE 的对称点为F ， ∴ADE ?≌FDE ?，

∴DA DF DC ==，90DFE A ∠=∠=?， ∴90DFG ∠=?， 在Rt DFG ?和Rt DCG ?中， ∵DF DC

DG DG =??

=?

∴Rt DFG ?≌Rt DCG ?（HL ）， ∴GF GC =；

（2）2BH AE =，理由是：

如图2，在线段AD 上截取AM ，使AM AE =，

∵AD AB =， ∴DM BE =，

由（1）知：12∠=∠，34∠=∠， ∵90ADC ∠=?，

∴123490∠+∠+∠+∠=?， ∴222390∠+∠=?， ∴2345∠+∠=?， 即45EDG ∠=?， ∵EH DE ⊥，

∴90DEH ∠=?，DEH ?是等腰直角三角形，

∴190AED BEH AED ∠+∠=∠+∠=?，DE EH =， ∴1BEH ∠=∠， 在DME ?和EBH ?中，

1DM BE BEH DE EH =??

∠=∠??=?

∴DME ?≌EBH ? ∴EM BH =，

Rt AEM ?中，90A ∠=?，AM AE =，

∴2EM AE

=，

∴2BH AE =；

【点睛】

本题考查了正方形的性质，全等三角形的判定定理和性质定理，对称的性质，等腰直角三角形的性质等知识，解决本题的关键是利用正方形的性质得到相等的边和相等的角，证明三角形全等，作出辅助线也是解决本题的关键． 8．（1）①7；②证明见解析；（2）93

，理由见解析 【分析】

（1）①如图1中，延长BC 交DE 的延长线于T ，过点T 作TH ⊥BD 于H ，设BD=2x ．证明△BDT 是等腰直角三角形，四边形ACTE 是矩形，进而利用勾股定理构建方程求解即可； ②如图2中，延长BC 交DE 的延长线于T ，连接TF ，进而利用全等三角形的性质证明△CEF 是等腰直角三角形即可解决问题；

（2）如图3中，根据题意设∠EAD=x ，则∠BAC=2x ．证明△ABC 是等边三角形，再根据垂线段最短即可解决问题． 【详解】

解：（1）①如图1中，延长BC 交DE 的延长线于T ，过点T 作TH ⊥BD 于H ，设BD=2x ．

∵∠ACB=90°，∠ACB+∠AED=180°， ∴∠AED=90°， ∵CA=CB ，EA=ED ， ∴∠B=∠D=45°， ∴∠BTD=90°，

∵∠TCA=∠CTE=∠TEA=90°，

∴四边形ACTE 是矩形， ∴52

EC AT ==， ∵TH ⊥BD ， ∴BH=HD=x ， ∴TH=HB=HD=x ， ∵AB=3， ∴AH=x-3， 在Rt △ATH 中，则有2

2252(())2

3x x =-+， 解得：72x =

或1

2

-（不符合题意舍弃）， ∴BD=2x=7．

②证明：如图2中，延长BC 交DE 的延长线于T ，连接TF ．

∵∠B=∠D=45°， ∴TB=TD ，

∵∠BTD=90°，BF=DF ， ∴TF ⊥BD ，∠FTE=∠BTF=45°， ∴TF=BF ，∠BFT=90°， ∵四边形ACTE 是矩形， ∴TE=AC ， ∴AC=BC ， ∴BC=TE ， ∵∠B=∠FTE=45°， ∴△FBC ≌△FTE （SAS ）， ∴FC=EF ，∠BFC=∠TFE ， ∴∠CFE=∠BFT=90°， ∴△CFE 是等腰直角三角形， ∴2EF ．

（2）如图3中，设∠EAD=x ，则∠BAC=2x ．

∵EA=ED ， ∴∠EAD=∠EDA=x ， ∴2x+∠AED=180°， ∵∠ACB+∠AED=180°， ∴∠ACB=2x ， ∵CB=CA ， ∴∠B=∠CAB=2x ， ∴∠C=∠B=∠CAB ， ∴△ABC 是等边三角形， ∴∠CAB=60°，∠EAD=30°， 当AD ⊥BC 时，△ADE 的面积最小， ∵AB=BC=AC=3， ∴32

2

AD =

， ∴S △ADE 的最小值132393

24==

． 【点睛】

本题属于三角形综合题，考查等腰直角三角形的判定和性质，等边三角形的判定和性质，矩形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．

9．（1）32323；（2）①见详解；②x=1；（3）△CDP 为等腰三角形时x 的值为：633-或3633+． 【分析】

（1）BP+DP 为点B 到D 两段折线的和．由两点间线段最短可知，连接DB ，若P 点落在BD 上，此时和最短，且为32AQ=x ，则QD=3-x ，PQ=x ．又PDQ=45°，所以QD 2PQ ，即2x ．求解可得答案；

（2）由已知条件对称分析，AB=BP=BC ，则∠BCP=∠BPC ，由∠BPM=∠BCM=90°，可得∠MPC=∠MCP ．那么若有MP=MD ，则结论可证．再分析新条件∠CPD=90°，易得①结论．②求x 的值，通常都是考虑勾股定理，选择直角三角形QDM ，发现QM ，DM ，QD 都可用x 来表示，进而易得方程，求解即可．

（3）若△CDP 为等腰三角形，则边CD 比为改等腰三角形的一腰或者底边．又P 点为A 点关于QB 的对称点，则AB=PB ，以点B 为圆心，以AB 的长为半径画弧，则P 点只能在弧AB 上．若CD 为腰，以点C 为圆心，以CD 的长为半径画弧，两弧交点即为使得△CDP 为等腰三角形（CD 为腰）的P 点．若CD 为底边，则作CD 的垂直平分线，其与弧AC 的交点即为使得△CDP 为等腰三角形（CD 为底）的P 点．则如图所示共有三个P 点，那么也共有3个Q 点．作辅助线，利用直角三角形性质求之即可． 【详解】

解：（1）连接DB ，若P 点落在BD 上，此时BP+DP 最短，如图：

由题意，∵正方形ABCD 的边长为3， ∴223332BD =+=， ∴BP ＋DP 的最小值是32；

由折叠的性质，PQ AQ x ==，则3QD x =-， ∵∠PDQ=45°，∠QPD=90°， ∴△QPD 是等腰直角三角形， ∴22QD QP x =

=，

∴32x x -=， 解得：323x =-； 故答案为：32；323-； （2）如图所示：

①证明：在正方形ABCD 中，有 AB=BC ，∠A=∠BCD=90°． ∵P 点为A 点关于BQ 的对称点， ∴AB=PB ，∠A=∠QPB=90°， ∴PB=BC ，∠BPM=∠BCM ，

∴∠BPC=∠BCP，

∴∠MPC=∠MPB-∠CPB=∠MCB-∠PCB=∠MCP，∴MP=MC．

在Rt△PDC中，

∵∠PDM=90°-∠PCM，

∠DPM=90°-∠MPC，

∴∠PDM=∠DPM，

∴MP=MD，

∴CM=MP=MD，即M为CD的中点．

②解：∵AQ=x，AD=3，

∴QD=3-x，PQ=x，CD=3．

在Rt△DPC中，

∵M为CD的中点，

∴DM=QM=CM=3

2

，

∴QM=PQ+PM=x+3

2

，

∴(x+3

2

)2＝(3?x)2+(

3

2

)2，

解得：x=1．

（3）如图，以点B为圆心，以AB的长为半径画弧，以点C为圆心，以CD的长为半径画弧，两弧分别交于P1，P3．此时△CDP1，△CDP3都为以CD为腰的等腰三角形．作CD的垂直平分线交弧AC于点P2，此时△CDP2以CD为底的等腰三角形．

；

①讨论P1，如图作辅助线，连接BP1、CP1，作QP1⊥BP1交AD于Q，过点P1，作EF⊥AD 于E，交BC于F．