分块矩阵的初等变换及应用_百度文库.

十.研究创新题
解:
1.分块矩阵的初等变换
分块矩阵的初等变换与初等矩阵
吴云在1997年8月的《工科数学》上的《分块矩阵的初等变换》一文中提到定义1分块矩阵的行(列初等变换是指:
(1)交换两行(列的位置;
(2)第i行(列的各个元素分别左乘(右乘该行(列的一个阶左(右保秩因子H;
(3)第i行(列的各个元素分别左乘(右乘一个阶矩阵K后加到第j行.
定义2 对应于分块矩阵的初等分块矩阵是指:
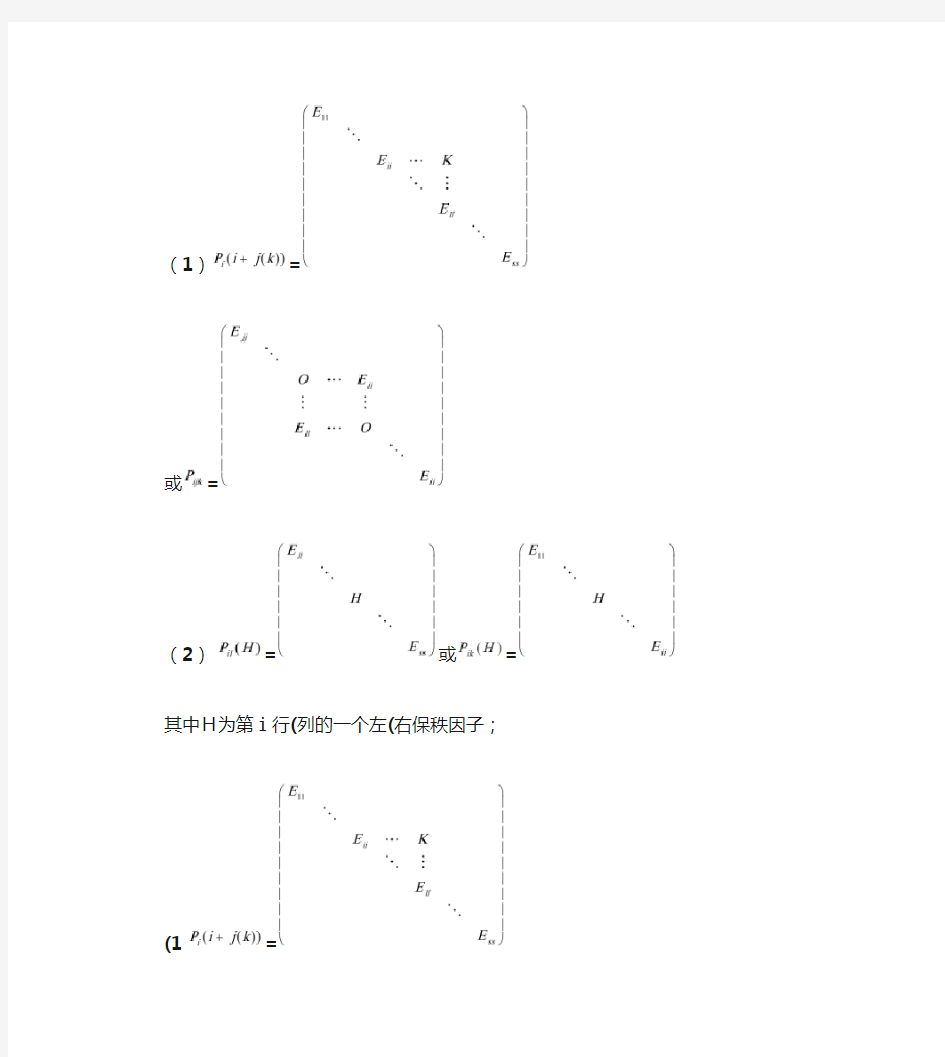
(1)=
或=
(2)=或=
其中H为第i行(列的一个左(右保秩因子;
(1 =
(2 或=
初等分块矩阵与通常的初等矩阵类似,但由于矩阵乘法不满足交换律,故需要分为左、右两种.直接验算可得:
定理1(1交换的第i行与第j行,相当于左乘一个m阶初等分块矩阵,其中中的元素为h(i阶单位矩阵,为h(j阶单位矩阵,
当r≠i且r≠j时,为h(r阶单位矩阵;交换的第i列与第j列相当于右乘一个n阶初等分块矩阵,其中为l(i阶单位矩阵,为l(j阶单位矩阵,当r≠i且r≠j时,为l(r阶单位矩阵;
(2 的第i行的每一个元素左乘一个矩阵H相当于左乘一个m阶分块矩阵
中H为h(i阶方阵; 的第i列的每一个元素右乘一个矩阵H,相当于
右乘一个n阶初等到变换矩阵,其中H为l(i阶方阵;
(3 的第j行的每个元素分别左乘一个h(i×h(j矩阵K后加到第i行,相当
于左乘一个初等分块矩阵;第j列的每一个元素分别右乘l(j×l(i矩阵K后加到第i列,相当于右乘.
定理2设A为方阵,则分块矩阵施行第一种行初等变换后,对应的行列式为
,
其中
h(i,j=h(ih(j-l+h(i+l]+…+h(j[h(i+h(i+j+…+h(j-l],
l(i,j=l(ih(j-l+l(i+l]+…+l(j[l(i+l(i+j+…+l(j-l],
施行第二种初等变换后,对应的行列式为|H|·|A|;施行第三种初等变换后,对应的行列式的值不变.
证明: ,显然成立.
下证,所在的第1行逐次与它相邻的行交换,移至前,共进行h(i-1+h(i+1+…+h(j-1次交换两行,第2行逐次与它相邻的行交换,移至前,同样进行相同次交换两行,依此类推,把所在的行移至所在的行前,共进行
h(i[h(i-1+h(i+1+…+h(j-1]次交换两行,然后把移至适当的位置,同理共进行h(j[h(i+h(i+1+…+h(j-1]次交换两行,所以交换两行的总次数为h(i,j,故
;同理.
所以有==(-1或==(-1)
==或=
====
定理3 分块矩阵进行初等变换后,秩不变.
证明: 对于(1,相当于对进行若干次行(列的交换,故命题成立;对于(2,根据定
义1,显然成立;对于(3,相当于进行若干次把行(列乘以一个倍数后加到另一行(列,故命题成立.
定理4 (1设A,B的行数均为m,则矩阵方程AX=B,当(A= (A,B=m时有唯一解,当(A= (A,B<m时有无穷多解,
当(A< (A,B时无解;
(2设A,B的列数均为n,则矩阵方程XA=B,当(A= =n时有唯一解,当(A= <n有无穷多解,
当(A< 时无解.
证明: (1设(A= (A,B<m,则存在可逆矩阵P,Q,使,
其中为r阶单位矩阵, 为r阶方阵,设,
则有: =
= =B
所以为AX=B的解,其中, 是任意的.
当(A= (A,B=m时,A=P(OQ,B=( ,显然,AX=B有唯一解: ;当(A< (A,B时,AX=B无解.
同理可证(2成立(当(A= ( , <n时,X=P
定义3 对于任意的u,v,如果( = ( ,= (,,
则称为极大元.
定理5 分块矩阵可以用分块矩阵的初等变换对角化的充要条件是: 它有一个极大元.
证明: 充分性.不妨设为极大元(否则可以通过第一种分块矩阵的初等变换把极大元移
到第一行,第一列交叉位置.由定理4,存在可逆矩阵P,Q,使
,,
令K=-P,其中, 为适当阶数的任意矩阵.则
K+ =,所以
第一行左乘K加到第二行,得.同理,令K'=-, 则K′+ =0,所以的第一列右乘K′后加到第二列,
得.
(如先进行列变换,再进行行变换,得,
因为=+=+,故两种运算顺序结果相同
必要性.反证法,不妨设(≠(,或(,(,则由定理4, =-或=-无解,从而不存在K,使对角化.同理,当(≠(,或(,≠(时,不存在使-A K=A或-=成立.
定理5表明:并不是所有的2×2分块矩阵都可以用分块矩阵初等变换对角化,如果分块矩阵没有极大元,则需分得更细,才能对角化.
定理6 矩阵的一种分块方法可以用分块矩阵的初等变换对角化的充分条件是:存在s-1行且存在t-1列有极大元.
证明: 用数学归纳法.当s=t=1时,只有一块,命题成立;
设s≤e,t≤ f时命题成立.当s=e+1,t=f时,存在e行且存在f-1列有
极大元,显然可以用第一种分块矩阵的初等变换,通过交换两行或两列的位置,使的前e行与前f-1列都有极大元,再把前e行,前f-1列看成一块,得到一个新的2×2分块矩阵,记为
.显然为极大元,根据定理4, 可以化成对角形: ,又,它的每行、列都有极大,故由假设可以对角化,从而可以对角化.同理可证当s=e,t=f+1时, 可以对角化.由此命题成立.
下面讨论对角化后的非零块进一步化简的方法.
设,与.根据
定理1, ,为的左(右保秩因子,显然也是所在行(列的左(右保秩因子,故对角化后的
分块矩阵第i行、第i列分别左乘,右乘后, 可以化成
讨论分块方阵行列式的计算,先讨论分块初等阵的行列式.
设I为S×S分块单位阵:
I=
其中I r为r阶单位阵(1≤i≤S,对I施行一次初等变换可得定义2所述的三种分块初等阵,它们的行列式有下列计算公式.
引理分块初等阵的行列式有以下性质:
(1|I(i,j|= ,其中τ=r (r+1+…+r+ r (r+1+…+ r-1(i
特别地,若j=i+1,则| I(i,j|=(-1 r r;
(2|I(i(K|=|k|,其中K是r阶可逆阵;
(3|I(j(K,i|=1,其中K是r×r矩阵.证
(1不难验证,将I(i,j的元素行进行τ次相邻的对调可将I(i,j变成I,由行列式的性
质,|I(i,j|= |I|=.
(2,(3由对角分块方阵及三角形分块方阵的行列式计算方法即知.
由于对分块方阵A施行一次初等行变换,相当于用相应的分块初等阵左乘A,由上述引理,我们有下列分块方阵的行列式计算性质.
定理7 设A是一个分块方阵.
(1交换|A|的i,j两行(列,行列式变为(-1τ|A|,
其中τ= r (r+1+…+ r+ r (r+1+…+ r-1;
特别地,交换|A|的相邻两行(列(i行和i+1行,行列式变为(-1 r r+1|A|;
(2用一个r阶可逆阵K左(右乘|A|的第i行(列的所有矩阵,等于用|K|乘以|A|;
(3用一个矩阵左(右乘|A|的某一行(列的所有矩阵再加到另一行(列的对应元素上,行列式不变.
由定理7的(2可得
推论分块行列式|A|的某一行(列的所有矩阵的可逆左(右因子K,可以行列式|K|的形式提到行列式符号外.
2.分块矩阵初等变换的应用
一、利用分块矩阵的初等变换求矩阵的逆.
廖中行在2002年05期《四川教育学院学报》上的《初等变换在分块矩阵乘法》的一文中提到
例1: 已知其中B是r×r可逆阵,C是s×s可逆阵,求证:P
可逆,并求.分析:本题是一个分块阵的求逆问题,一般可用待定子块法,也可利用广义初等变换span,还可用左乘分块初等阵的方法.解:因B、C可逆,故|B|≠0,|C|≠0.根据拉普拉斯展开,有
≠0,故P可逆.求C有三种办法:
解法一:利用广义初等行变换法.
B r,
C r
(B D+r
故P=
本题对分块矩阵进行广义初等变换是一般矩阵的初等变换的一种推广,其方法和一般矩阵相同.作初等行(列变换时,对矩阵P应左(右乘相应的分块单位阵.上述分块初等变换的过程也可用分块阵左乘相应的分块初等阵,可表示如下:
解法二: 可用左乘分块初等阵的方法求
=
有=
即:==E
故有P===
例2:已知A=,求A.
分析:本题是一个矩阵的求逆问题,一般可用公式法,矩阵的初等变换法求;可以用分
块矩阵初等变换法求.
利用分块矩阵初等变换法
先A化分成分块矩阵,即A==
其中B=,C=,D=
从而求得B=,C=
然后对A进行广义初等变换,即:
B r,
C r
(B D r+r
A==
如果用其它方法来求解将会变得很繁琐,用分块矩阵的初等变换发来求解就显的比较简单.
二、利用分块矩阵初等变换求行列式的值
宋玉英在2002年04期的《兰州教育学院学报》上的《“用广义初等变换”法求“分
块矩阵”的逆矩阵》一文中提到
例3设P=是一个分块方阵,其中A是r阶可逆阵,求|P|.
解: 由推论及定理7的(3:
====
若A与D可乘,则|P|=|AD-ACAB|;又若A与C可交换(即AC=CA,则|P|=|AD-CB|.例
例4 设D=, 其中a≠0,求|A|
解: D==
由于A,C可交换,所以
D=== =|(ad-bcI|=(ad-bc
例5 设A,B,C和D是n阶方阵,试证明=
证两次利用定理4的(1,得
=(-1)=(-1)(-1)=
三、利用分块矩阵的初等变换求矩阵的秩
史永铨在2002年02期《淮南师范学院学报》上的《分块矩阵初等变换及其应用》
一文中提到:
矩阵的秩有以下初等性质:
设A与B分别是r×s与p×q矩阵,则r≥r(A+r(B
并且当A(或B是方阵且非异时,或者C=0时上式的等号成立.
例6. 设A是m×n阵的非异顺序主子阵,
则r=r(A+r(D-CAB
证:=
而A是非异阵,由以上性质知r=≥r(A+r(D
考情解读B
例7. 设n阶方阵A=(Q为反对称矩阵,证明:r
2必为偶数
(1: 对n用归纳法
n=1,2是命题显然成立
设阶数小于n时命题为真则对n阶及对称矩阵A,将A分块成
A=,其中A=不妨设
(30.
=
∴r(A=r=r
=r(A+r作函数图象有两种基本方法:一是描点法,二是图象变换法,其中图象变换有平移变换、伸缩变换、对称变换.C4
=2+r(D-BAC
但D-BAC为阶数比A低的反对称矩阵,由归纳假设r(D-BAC为偶数,
故r(A为偶数.
四、分块矩阵的初等变换在矩阵分解中的应用
例8. 设A=(a是n阶方阵,它的顺序主子式全不为零,
证明: 存在非异下三角形矩阵B与非异上三角形矩阵C,使A=BC
证: 对n用归纳法
n=1时显然成立
设当n-1时,结论成立,则对n,将A分块成A=
由归纳假设对A=有A=BC其中BC分别是n-1阶非异下三角形与上三角形矩阵
,其中b=-
上式两端取行列式有:=b,
b0
=
于是得:A==BC
其中B===,
C=
=0,=b
B与C分别是非奇异的下三角与上三角形矩阵.
类似的例子还可以举出很多,由于篇幅有限,不再赘述.总之,在矩阵乘法中,只要对矩阵进行恰当的分块,结合矩阵初等变换的方法,就能大大的简化其运算.
