全等三角形辅助线系列之一---角平分线类辅助线作法大全说课讲解

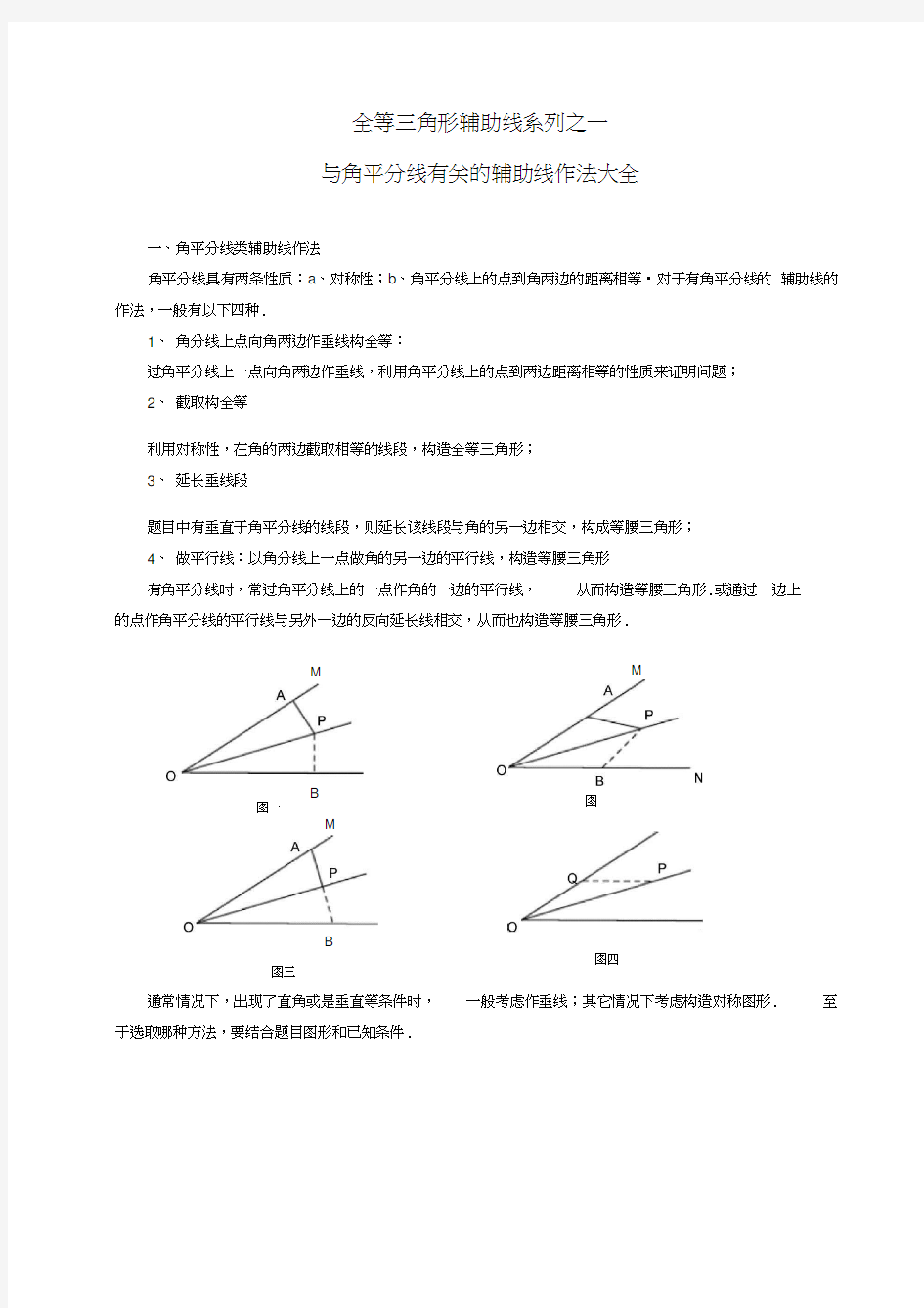
全等三角形辅助线系列之一 与角平分线有关的辅助线作法大全一、角平分线类辅助线作法角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等•对于有角平分线的 辅助线的作法，一般有以下四种.1、 角分线上点向角两边作垂线构全等：过角平分线上一点向角两边作垂线，利用角平分线上的点到两边距离相等的性质来证明问题； 2、 截取构全等利用对称性，在角的两边截取相等的线段，构造全等三角形； 3、 延长垂线段题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交，构成等腰三角形； 4、 做平行线：以角分线上一点做角的另一边的平行线，构造等腰三角形 有角平分线时，常过角平分线上的一点作角的一边的平行线，从而构造等腰三角形.或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交，从而也构造等腰三角形.通常情况下，出现了直角或是垂直等条件时， 一般考虑作垂线；其它情况下考虑构造对称图形. 至于选取哪种方法，要结合题目图形和已知条件.图四MB图一M图MB图三典型例题精讲【例1】如图所示，BN平分/ ABC, P为BN上的一点，并且PD丄BC于D, AB+ BC 2BD .求证：BAP+ BCP 180 .【解析】过点P作PE丄AB于点E.VPE± AB, PD 丄BC, BN 平分/ABC,：PE PD .在Rt APBE 和Rt APBC 中，BP BPPE PD•••Rt z2PBE 细t ^BC ( HL), BE BD .T AB BC 2BD , BC CD BD , AB BE AE , • AE CD .••PE丄AB, PD 丄BC ,• PEB PDB 90 .在AFAE 和Rt APCD 中，PE PDPEB PDC ,AE DC• △AE织t A^CD , • PCB EAP .•/ BAP EAP 180 , • BAP BCP 180 .【答案】见解析.EP【解析】因为已知PD平分/ ADC，所以我们过P点作PE丄CD，垂足为E,则PA PE ,由P是AB 的中点，得PB PE，即CP平分/ DCB .【答案】作PE丄CD，垂足为E，••• PEC A 90 ，••• PD 平分 / ADC，• PA PE，又•/ B PEC 90，• PB PE，•••点P在/ DCB的平分线上，• CP 平分/ DCB .【例3】已知：AOB 90，OM是/ AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA、OB交于C、D .(1) PC和PD有怎样的数量关系是____________(2) 请你证明(1)得出的结论.【解析】(1) PC PD .(2)过P 分别作PE 丄OB 于E , PF 丄OA 于F , ••• CFP DEP 90 ,•••OM 是/AOB 的平分线，• PE PF , •/1 FPD 90，且AOB 90,• FPE 90 ,• 2 FPD 90 , • 1 2 ,在△CFP 和ADEP 中CPF DEP PF PE , AZCFP 也zDEP ,• PC PD .1 2【答案】见解析.如图①，OP 是/ MON 的平分线，请你利用该图形画一对以形•请你参考这个作全等三角形的方法，解答下列问题： (1)如图②，在△ ABC 中，/ ACB 是直角，B 60 , AD 、CE 分别是/ BAC 、/ BCA 的平分线，AD 、CE 相交于点F ，请你判断并写出 FE 与FD 之间的数量关系(不需证明)；(2)如图③，在△ ABC 中，B 60，请问，在(1)中所得结论是否仍然成立？若成立, 请证明；若不成立，请说明理由.【解析】如图①所示;(1) FE FD .【例4】 OP 所在直线为对称轴的全等三角图①(2)如图，过点F作FG丄AB于G,作FH丄BC于H，作FK丄AC于K,••AD、CE 分别是/BAC、/BCA 的平分线，二FG FH FK ,在四边形BGFH 中，GFH 360 60 90 2 120 ,••AD、CE分别是/BAC、/BCA的平分线， B 60 ,••• FAC FCA 1 180 60 60 .2在△AFC 中，AFC 180 FAC FCA 180 60 120 ,在AEFG和ADFH中,EFG DFHEGF DHF , AZEFG 也Q FH ,二FE FDFG FH【答案】见解析.120 , AC 平分/ MAN，点B、D 分别在AN、AM 上.1AC B 30后再可以证得AD AB严，从而，证得结论;(2)过点C分别作AM、AN的垂线，垂足分别为E、F，证得△ CED BJCFB后即可得到EFD AFC 120 ,EFG DFH ,【例5】已知MAN(1)如图1，若ABC之；(2)如图2,若ABC 若不成立，请说明理由.ADC 90ADC 180，请你探索线段AD、AB、AC之间的数量关系，并证明【解析】(1)得到ACD，则(1)中的结论是否仍然成立？若成立, 给出证明;AD AB AE ED AF FB AE AF，从而证得结论.【答案】（1 ）关系是：AD AB AC .证明：••• AC 平分/MAN , MAN 120• CAD CAB 60又ADC ABC 90 ,• ACD ACB 30贝U AD AB 1AC （直角二角形一锐角为30 ，则它所对直角边为斜边一半）2二AD AB AC ；(2 )仍成立.证明：过点C分别作AM、AN的垂线，垂足分别为E、F••AC 平分/MAN•••CE CF (角平分线上点到角两边距离相等)•ABC ADC 180 , ADC CDE 180•CDE ABC又CED CFB 90 ,z.JCED ^/CFB (AAS )•ED FB ,•AD AB AE ED AF FB AE AF由(1)知AE AF AC ,• AD AB AC .【例6】 如图，在△ ABC 中， C 2 B , AD 平分/ BAC ，求证： AB AC CD .AED=2【答案】见解析.【解析】在BC 上截取E 点使BE BA ，连结DE .• BD 平分 ABC , • ABD EBD .在ABD 与EBD 中• AB EB ,ABD EBD , BD BD• ABD 也 EBD ,• A DEB• AB AE , •- BAD BED , •- DEC 72 又• ADB 36 18 54 , • CDE 72【解析】在AB 上截取点E ,使得AEAC . ••AD 平分/BAC ,「. EADCAD ,•••公DE ^zADC ( SAS ) . •• AED C, ED CD . • AED B EDBB EDB ,• BE DE .• CD BE ABAEAB AC .【例7】如图，△ ABC 中, AB AC , A 108 , BD 平分 ABC 交 AC 于 D 点.求证：BC AC CD .CDE DEC , ••• CD CEBE EC , •-BCAC CD【答案】见解析.O , 【例8】已知ABC 中，A 60 ,BD、CE分别平分ABC和ACB ,BD、CE交于点试判断BE CD、BC的数量关系，并加以证明.在根据BOC 120【解析】在BC上截取一点F使得BF BE，易证BOE BOF，推出BOE COF 60，再证明OCF S OCD即可.【答案】BC BE CD .【例9】如图：已知AD ABC的中线，且1求证: BE CF EF .【解析】在DA上截取DN DB，连接NE, NF, 则DN DC在ADBE和ADNE中:DN DB1 2ED ED•••ZDBE ^zDNE ( SAS), /• BE NE同理可得：CF NF在AEFN中，EN FN EF (三角形两边之和大于第三边)•BE CF EF •【答案】见解析.【例10】已知：在四边形ABCD中，BC BA , A C 180，且 C 60 , BD平分/ ABC,求证: BC AB DC •【解析】在BC上截取BE BA ,••BD 平分/ABC, • ABD EBD ,在ABAD和ABED中，BA BEABD EBD ,BD BD.•./BAD BA ED, •AD DE , A BED• BED DEC180 , A C180•C DEC , • DE DC • • DC AD ••••DE CD CE ,••• BC BE CE AB CD .【答案】见解析.【例11】观察、猜想、探究：在厶ABC 中，ACB 2 B .(1)如图①，当 C 90 , AD为/ BAC的角平分线时，求证：AB AC CD ;(2)如图②，当 C 90 , AD为/ BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想；(3)如图③，当AD ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明.【解析】(1)过D作DE丄AB，交AB于点E,理由角平分线性质得到ED=CD，利用HL得到直角三角形AED 与直角三角形ACD全等，由全等三角形的对应边相等，对应角相等，得到AE AC , AED ACB，由ACB 2 B，利用等量代换及外角性质得到一对角相等，利用等角对等边得到BEDE ,由AB AE EB，等量代换即可得证；(2)AB CD AC，理由为：在AB上截取AG AC，如图2所示，由角平分线定义得到一对角相等，再由AD AD，利用SAS得到三角形AGD与三角形ACD全等，接下来同(1) 即可得证；(3)AB CD AC，理由为：在AF上截取AG AC，如图3所示，同(2)即可得证.【答案】(1 )过D作DE丄AB,交AB于点E,如图1所示，VAD 为/BAC 的平分线，DC 丄AC, DE 丄AB, • DE DC ,在Rt △ACD 和Rt △AED 中，AD AD ，DE DC ，•••Rt△KCD 职△AED ( HL ) , /• AC AE , ACB AED ,••• ACB 2 B ,• AED 2 B ,又:AED B EDB , • B EDB ,•BE DE DC ，则AB BE AE CD AC ；( 2) AB CD AC ，理由为：在AB 上截取AG AC ，如图 2 所示，•••AD 为/BAC 的平分线，• GAD CAD ,AG AC••在^ADG 和A ADC 中，GAD CADAD AD• ZADG 也zADC ( SAS), • CD CG , AGD ACB ,•ACB 2 B ，• AGD 2 B ，又• AGD B GDB , • B GDB ,•BE DG DC ，则AB BG AG CD AC；( 3) AB CD AC ，理由为：在AF 上截取AG AC ，如图 3 所示，••AD 为/FAC 的平分线，• GAD CAD ,••在^ADG 和A ADC 中，AG ACGAD CAD , •△X DG 也ZADC (SAS),AD AD•CD GD ，AGD ACD ，即ACB FGD ，•ACB 2 B ,• FGD 2 B，又• FGD B GDB , • BG DG DC ，则B GDB ，AB BG AG CD AC ．【例12】如图所示，在△ ABC 中， ABC 3 C , AD 是/ BAC 的平分线，BE 丄AD 于F .1求证：BE AC AB .2【解析】延长BE 交AC 于点F .则AD 为/BAC 的对称轴,••BE 丄AD 于F ,•••点B 和点F 关于AD 对称，BE EF-BF 2,AB AF , ABF AFB .ABF + FBC ABC 3 C , ABFAFBFBC + C ,FBC + C + FBC 3 C ,FBC C , / • FB FC ,1 BE -FC21 2AC AF1AC AB 21•BE AC AB2【答案】见解析.E-B【例13】如图，已知：△ ABC中AD垂直于/ C的平分线于D, DE // BC交AB于E.求证：EA EB .【解析】由AD垂直于/C的平分线于D，可以想到等腰三角形中的三线合一，于是延长AD交BC与点F，得D是AF的中点，又因为DE //BC，由三角形中位线定理得EA EB .【答案】延长AD交BC与点F,••CD 平分Z ACF ,••• 1 2，又AD 丄CD ,•••从DC 迫FDC ,• AD FD ,又'/DE //BC,• EA EB .【解析】延长BE交AC于M ,•••BE 丄AE ,• AEB AEM 903 90 1同理， 4 90 24 , • AB AM【例14】已知：如图，在△ ABC中，ABC 3 C , 1 2 , BE丄AE.求证：AC AB 2BE .在A ABE 中，•/1 3 AEB 180 ,•••BE丄AE,「. BM 2BE ,••• AC AB AC AM CM ,• 2是厶BCM的外角，• 4 5 C•/ ABC 3 C，…ABC3 5 4 5• 3 C 4 5 25C ,••• 5 C•CM BM , ••AC AB BM2BE【答案】见解析.【例15】如图，已知AB AC, BAC90 , BD为/ ABC的平分线，CE 丄BE,求证：BD 2CE .【解析】延长CE，交BA的延长线于点F .••BD为/ABC的平分线，CE丄BE,• ZBEF^zBEC ,• BC BF , CE FE .BAC 90 , CE丄BE,「. ABD ACF ,又• AB AC , •^ABD 也ZACF, • BD CF . • BD 2CE .【答案】见解析.A课后复习【作业1】如图所示，在△ABC中，BP、CP分别是/ ABC的外角的平分线，求证：点P在/ A的平分线上.【解析】过点P作PE丄AB于点E, PG丄AC于点G, PF丄BC于点F.因为P在/EBC的平分线上，PE丄AB, PH丄BC,所以PE PF . 同理可证PF PG .所以PG PE ,又PE丄AB, PG丄AC,所以P在/A的平分线上,【答案】见解析.BAD CAD , DA DB，求证：DC 丄AC.【作业2】已知：如图，AB 2AC ,1【解析】在AB 上取中点E ,连接DE ，则AE BE -AB • 2•/0A DB ,.・.DE 丄AB , AED 90又••• AB 2AC , ••AE AC .•/ BAD CAD,AZADE 也 ZADC( SAS ) • AEDACD 90 ，即 DC 丄 AC .【答案】见解析.【解析】如图，在 BC 上截取BE BD ，连接DE ,过 D 作 DF // BC ，交 AB 于 F ，于是 3 2 , ADF ECD •又••• 1 2 ,••• 13，故DF BF .显然FBCD 是等腰梯形.•BF DC , DFDC .•/ 2 1ABC1 1180 10020 ,22 2BEDBDE 1180280 ,2• DEC180BED 100，•‘FADDEC 100 , /-AFD 也 EDC , AD EC又T BE BD , • BC BDEC BD AD .【答案】见解析.【作业3】已知等腰 ABC , A 100 , ABC 的平分线交 AC 于D ，则BD AD BC •C【作业4】如图，已知在厶ABC 中，AD 、AE 分别为△ ABC 的内、外角平分线，过顶点交AD 的延长线于F ，连接FC 并延长交AE 于M .求证：AM ME .【解析】延长 AC ,交BF 的延长线于点N .••AD 平分/BAC , BF 丄 AD , A ^X FB^ZA FN ,二 BF NF . ••AD 、AE 分别为△ ABC 的内、外角平分线，••• EA 丄FA . VBF 丄 AF ,「.BF //AE .• BF :ME CF : CM , FN : AM CF : CM . •BF NF ,• AM ME .【答案】见解析.EFNB 作BF 丄AD,。