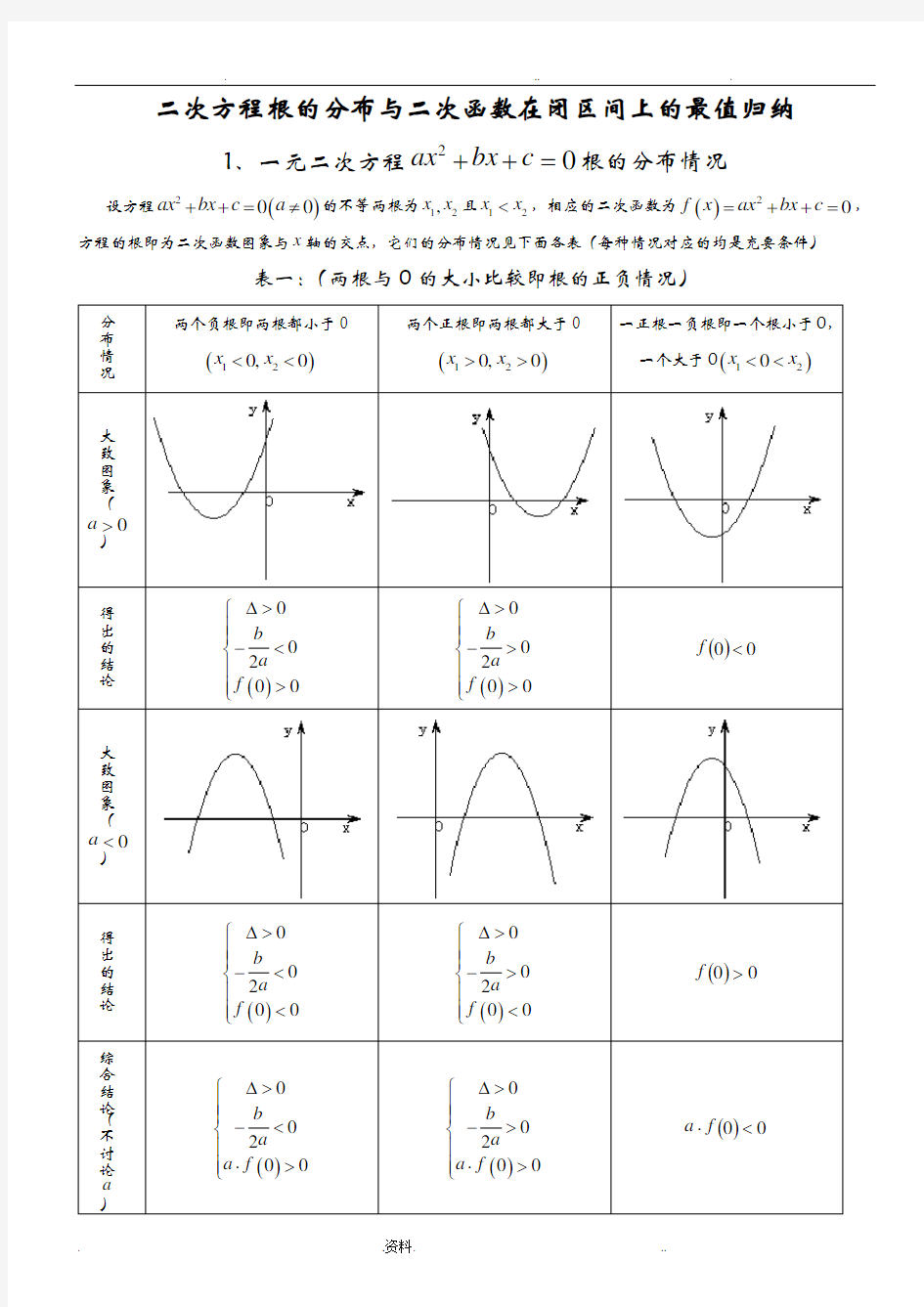
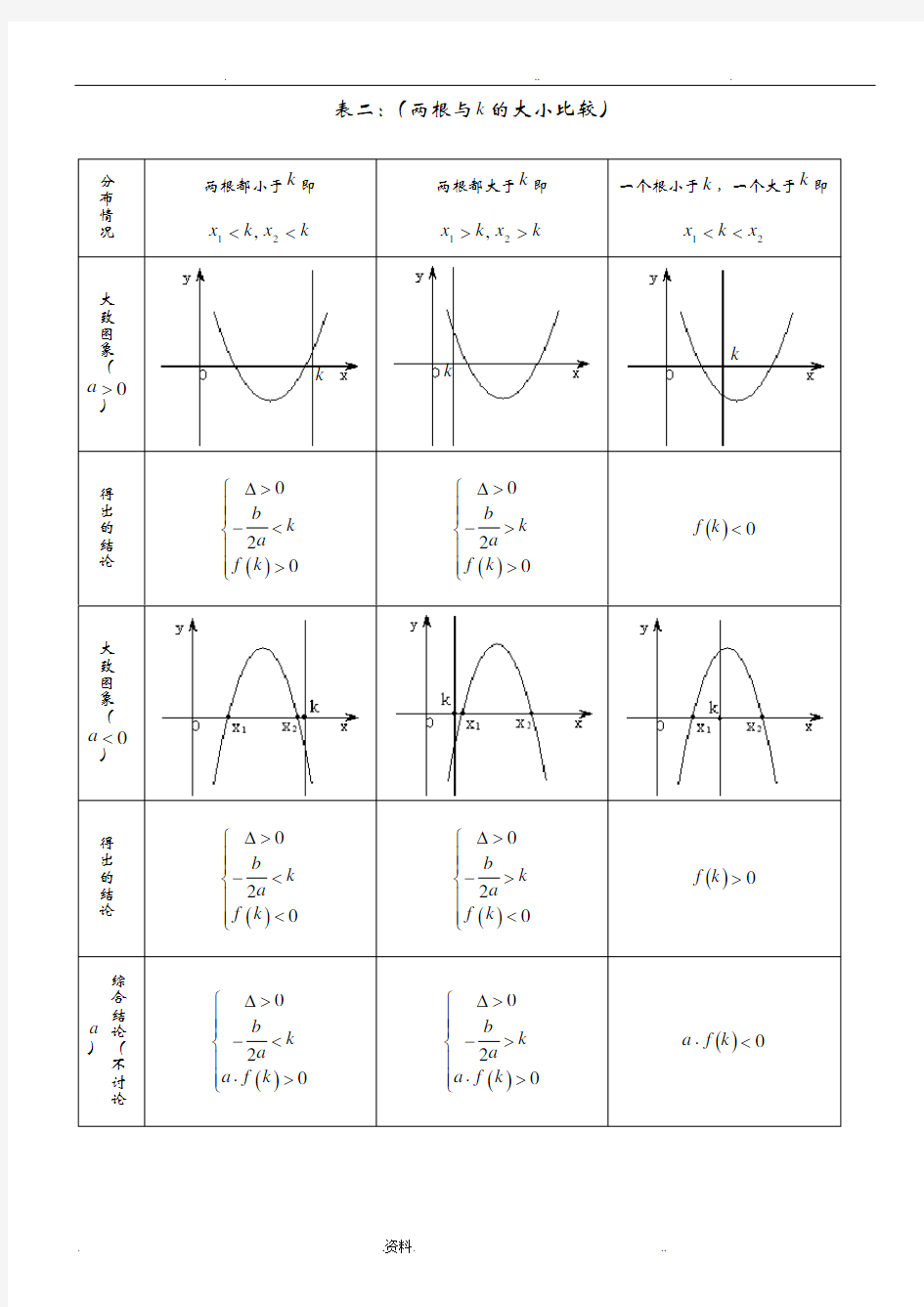
得出的结论
()()0002f m f n b m n
a ?>??
()()0
()()()()0000
f
m f n f p f q ???>??
或()()()()
0f m f n f p f q
综合结论(不讨论
a
)
——————
()()0
()()()()???
?
?<<0
0q f p f n f m f 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)
需满足的条件是
(1)0a >时,()()00f m f n
f m f n >???>??
对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,有以下特殊情况:
1? 若()0f m =或()0f n =,
则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,,从而可以求出参数的值。如方程()2
220
mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2
m
,由213
m <<得
2
23
m <<即为所求; 2? 方程有且只有一根,且这个根在区间()n m ,,即0?=,此时由0?=可以求出参数的值,然后再将参数的
值带入方程,求出相应的根,检验根是否在给定的区间,如若不在,舍去相应的参数。如方程2
4260x mx m -++=有且一根在区间()3,0-,求m 的取值围。分析:①由()()300f f -<即()()141530m m ++<得出
15314m -<<-
;②由0?=即()2
164260m m -+=得出1m =-或32
m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =?-,故3
2
m =不满足题意;综上分析,得出15314m -<<-或
1m =-
根的分布练习题
例1、已知二次方程()()2
21210m x mx m +-+-=有一正根和一负根,数m 的取值围。
解:由 ()()2100m f +< 即 ()()2110m m +-<,从而得1
12
m -<<即为所求的围。
例2、已知方程()2
210x m x m -++=有两个不等正实根,数m 的取值围。
解:由
()()0102200m f ?>??
-+?->?
?>??
? ()2
18010
m m m m ?+->?>-??>? ? 3
30m m m ?<->+
??>??? 03m <<-3m >+
例3、已知二次函数()()()222433y m x m x m =+-+++与x 轴有两个交点,一个大于1,一个小于1,数m 的取值围。
解:由 ()()210m f +< 即 ()()2210m m ++< ? 1
22
m -<<即为所求的围。
例4、已知二次方程()2
2340mx m x +-+=只有一个正根且这个根小于1,数m 的取值围。
解:由题意有方程在区间()0,1上只有一个正根,则()()010f f < ? ()4310m +< ? 1
3
m <-即为所求围。
(注:本题对于可能出现的特殊情况方程有且只有一根且这个根在()0,1,由0?=计算检验,均不复合题意,
计算量稍大)
2、二次函数在闭区间[]n m ,上的最大、最小值问题探讨
设()()002
>=++=a c bx ax x f ,则二次函数在闭区间[]n m ,上的最大、最小值有如下的分布情况:
a
b n m 2-
<< n a b m <-
<2即[]n m a
b ,2∈- n m a
b
<<-
2 图象
最大、最小值 ()()
()()
n f x f m f x f ==min max
()()(){}
()?
?
?
??-==a b f x f m f n f x f 2,max min max
()()
()()
m f x f n f x f ==min max
(1)若[]n m a b
,2∈-,则()()()????????? ??-=n f a b f m f x f ,2,max max ,()()()?
????????
??-=n f a b f m f x f ,2,min min ; (2)若[]n m a
b
,2?-,则()()(){}n f m f x f ,m ax max =,()()(){}n f m f x f ,m in min = 另外,当二次函数开口向上时,自变量的取值离开x 轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开x 轴越远,则对应的函数值越小。
二次函数在闭区间上的最值练习
二次函数在闭区间上求最值,讨论的情况无非就是从三个方面入手:开口方向、对称轴以及闭区间,以下三个例题各代表一种情况。
例1、函数()()2
220f x ax ax b a =-++≠在[]2,3上有最大值5和最小值2,求,a b 的值。
解:对称轴[]012,3x =?,故函数()f x 在区间[]2,3上单调。
(1)当0a >时,函数()f x 在区间[]2,3上是增函数,故()()()()max min
32f x f f x f ?=??=?? ? 32522a b b ++=??+=? ? 10a b =??=?; (2)当0a <时,函数()f x 在区间[]2,3上是减函数,故()()()()max min
23f x f f x f ?=?
?
=?? ? 25322b a b +=??++=?? 13a b =-??
=?
例2、求函数()[]221,1,3f x x ax x =-+∈的最小值。 解:对称轴0x a =
(1)当1a <时,()min 122y f a ==-; (2)当13a ≤≤时,()2min 1y f a a ==-; (3)当3a >时,()min 3106y f a ==-
改:1.本题若修改为求函数的最大值,过程又如何?
解:(1)当2a <时,()()max 3106f x f a ==-; (2)当2a ≥时,()()max 122f x f a ==-。
2.本题若修改为求函数的最值,讨论又该怎样进行?
解:(1)当1a <时,()()max 3106f x f a ==-,()()min 122f x f a ==-;
(2)当12a ≤<时, ()()max 3106f x f a ==-,()()2
min 1f x f a a ==-;
(3)当23a ≤<时,()()max 122f x f a ==-,()()2
min 1f x f a a ==-;
(4)当3a ≥时, ()()max 122f x f a ==-,()()min 3106f x f a ==-。
例3、求函数2
43y x x =-+在区间[],1t t +上的最小值。
解:对称轴02x =
(1)当2t <即2t >时,()2
min 43y f t t t ==-+;
(2)当21t t ≤≤+即12t ≤≤时,()min 21y f ==-; (3)当21t >+即1t <时,()2
min 12y f t t t =+=-
例4、讨论函数()2
1f x x x a =+-+的最小值。
解:()22
21,11,x a
x x a f x x x a x a
x x a ≥?+-+=+-+=?<-++?,这个函数是一个分段函数,由于上下两段上的对称轴分别为
直线12x =-
,12x =,当12a <-,1122a -≤<,1
2
a ≥时原函数的图象分别如下(1),(2),(3)
因此,(1)当
1
2
a<-时,()min13
24
f x f a
??
=-=-
?
??
;
(2)当
11
22
a
-≤<时,()()2
min
1
f x f a a
==+;
(3)当
1
2
a≥时,()min13
24
f x f a
??
==+
?
??
以上容是自己研究整理,有什么错误的地方,欢迎各位指正,不胜感激!