傅立叶变换与拉普拉斯变换

附录A 傅里叶变换
1 周期信号的频谱分析——傅里叶级数FS
狄立赫雷条件:在同一个周期1T 内,间断点的个数有限;极大值和极小值的数目有限;信号绝对可积∞
dt t f T 1
)(。
傅里叶级数:正交函数线性组合。 正交函数集可以是三角函数集
}:sin ,cos ,1{11N n t n t n ∈ωω或复指数函数集
}:{1Z n e t jn ∈ω,函数周期为T 1
,角频率为1
1122T f π=π=ω。
任何满足狄义赫利条件周期函数都可展成傅里叶级数。 傅里叶级数:
∑∞
=ω+ω+
=1
110)sin ()(n n n t n b t con a a t f
系数n a 和n b 统称为三角形式的傅里叶级数系数,简称傅里叶系数。
称11111/()f T f ω==为信号的基波、基频;1(,2~)i nf i n ω=为信号的n 次谐波。
根据欧拉公式:cos ,sin 22in t in t in t in t
e e e e n t n t i
ωωωωωω--+-== 复指数形式的傅里叶级数: ∑∞
-∞
=ω=
n t jn n e F t f 1
)(
(1) 周期信号的傅里叶频谱:
(i) 称{}n F 为信号的傅里叶复数频谱,简称傅里叶级数谱或FS 谱。 (ii)称{}n F 为信号的傅里叶复数幅度频谱,简称FS 幅度谱。
(iii)称{}n ?为傅里叶复数相位频谱,简称FS 相位谱。
(iv)周期信号的FS 频谱仅在一些离散点角频率1ωn (或频率1nf )上有值。 (v)FS 也被称为傅里叶离散谱,离散间隔为11/2T π=ω。
(vi)FS 谱、FS 幅度谱和相位谱图中表示相应频谱、频谱幅度和频谱相位的离散线段被称为谱线、幅度谱线和相位谱线,分别表示FS 频谱的值、幅度和相位 2 非周期信号的频谱分析—傅里叶变换(FT)
(1) 信号f (t )的傅里叶变换:[]
)()()(t f F dt e
t f F t
j ?
∞
∞-ω-==ω?
是信号)(t f 的频谱密度函数或FT 频谱,简称为频谱(函数)。
(2) 频谱密度函数)(ωF 的逆傅里叶变换为:
[]
)(?)(21
)(1ω=
ωωπ
=-∞
∞
-ω?
F F d e F t f t j (3) 称t j e ω-为FT 的变换核函数,t j e ω为IFT 的变换核函数。
(4) FT 与IFT 具有唯一性。如果两个函数的FT 或IFT 相等,则这两个函数必然相等。 (5) FT 具有可逆性。如果[])()(ω=F t f F ,则必有[])()(1t f F F =ω-;反之亦然。 (6) 信号的傅里叶变换一般为复值函数,可写成
)
()()(ω?ω=ωj e F F
(i) 称)(ωF 为幅度频谱密度函数,简称幅度谱,表示信号的幅度密度随频率变化的幅频特性; (ii) 称())()(ω=ω?F Arg 为相位频谱密度函数,简称相位谱函数,表示信号的相位随频率变化的相频特性。
(7) FT 频谱可分解为实部和虚部:)
()()(ω+ω=ωi r jF F F
)
()
(arctan )(,)()()(22ωω=ω?ω+ω=ωr i
i r F F F F F
()())(sin )()(,)(cos )()(ω?ω=ωω?ω=ωF F F F i r
(8) FT 存在的充分条件:时域信号)(t f 绝对可积,即?
∞∞
-∞
注意:这不必要条件。有一些并非绝对可积的信号也有FT 。 (2) FT 及IFT 在赫兹域的定义:
?∞
∞
-π-=
dt e t f f F ft j 2)()(;?∞
∞-π=
df
e
f F t f ft
j 2)()(
(3) 比较FS 和FT :
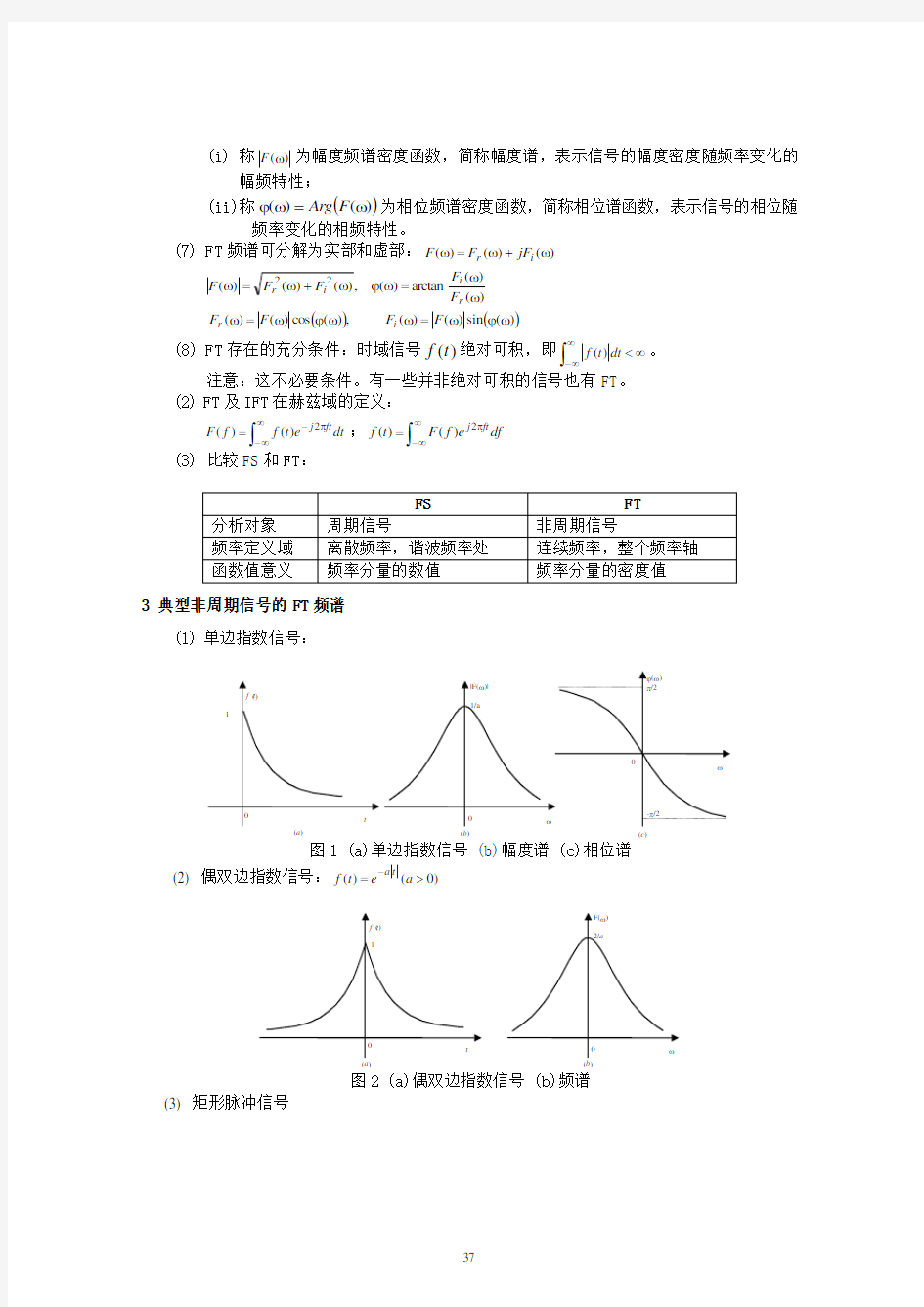
3 典型非周期信号的FT 频谱 (1) 单边指数信号:
ω
ω
|F(ω)|
1/a
?(ω) π/2 -π/2 0 0
t 0
1
f (t ) (a )
(b )
(c )
图1 (a)单边指数信号 (b)幅度谱 (c)相位谱
(2) 偶双边指数信号:)0()(>=-a e t f t a
ω
F(ω) 2/a
0 t 0 1
f (t ) (a )
(b )
图2 (a)偶双边指数信号 (b)频谱
(3) 矩形脉冲信号
F (ω)
E τ=矩形脉冲面积
0 τπ2 τπ4
τπ
6 ω
-τ/2 0 τ/2 t
f (t )=)(t EG τ E
(a ) (b )
图3 (a)矩形脉冲信号 (b)频谱
(4) 符号函数:不满足绝对可积条件,但存在FT 。
|F(ω)|
-a a ω (b )Sgn(t)
1
0 t
-1
(a )
图5 (a)符号函数 (b)频谱
(5) 阶跃信号:不满足绝对可积条件,但存在FT
|F(ω)| (π)
0 ω
u(t)
1
0 t
图6 单位阶跃函数及其幅度谱
附录B 拉普拉斯变换及反变换 一.拉普拉斯变换及逆变换
定义式:设有一时间函数f(t) [0,∞] 或 0≤t≤∞单边函数
)s (F t d e )t (f t s =?
∞
-
-0
其中,S=σ+jω 是复参变量,称为复频率。
左端的定积分称为拉普拉斯积分,又称为f(t)的拉普拉斯变换; 右端的F(S)是拉普拉斯积分的结果,此积分把时域中的单边函数f(t)变换为以复频率S 为自变量的复频域函数F(S),称为f(t)的拉普拉斯象函数。
以上的拉普拉斯变换是对单边函数的拉普拉斯变换,称为单边拉普拉斯变换。
如f(t)是定义在整个时间轴上的函数,可将其乘以单位阶跃函数,即变为f(t)ε(t ),则拉普拉斯变换为
