六种三角函数性质

六种三角函数性质、公式

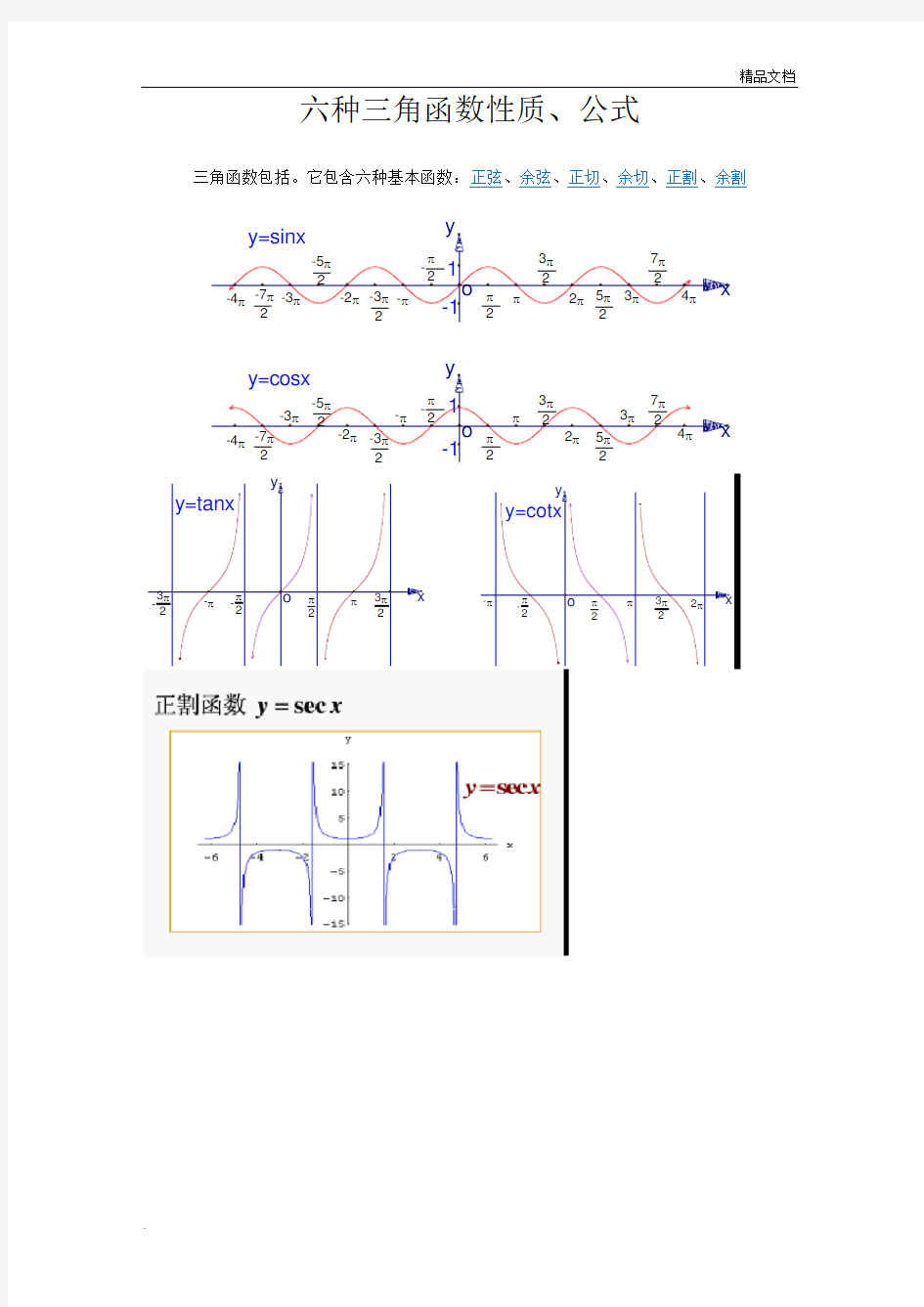
三角函数包括。它包含六种基本函数：正弦、余弦

、正切、余切、正割、余割

1-1y=sinx

-3π2

-5π2

-7π2

7π2

5π

2

3π2

π2

-π2

-4π-3π

-2π4π

3π

2ππ

-π

o

y x

1-1y=cosx

-3π

2

-5π2

-7π

2

7π2

5π2

3π2

π2

-π2

-4π-3π-2π4π

3π

2π

π

-π

o

y

x

y=tanx

3π2

π

π2

-

3π2

-π

-

π2

o

y

x

y=cotx

3π2

π

π2

2π

-π

-

π2

o

y

x

.反三角函数：

arcsinx

arccosx

arctanx arccotx

函数y=sinx y=cosx y=tanx y=cotx

定义域R R ｛x｜x∈R且

x≠kπ+

2

π

,k∈Z｝

｛x｜x∈R且

x≠kπ,k∈Z｝

值域［-1，1］x=2kπ+

2

π

时

y max=1

x=2kπ-

2

π

时y min=-1

［-1,1］

x=2kπ时y max=1

x=2kπ+π时

y min=-1

R

无最大值

无最小值

R

无最大值

无最小值

周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数

单调性在［2kπ-

2

π

,2kπ+

2

π

］

上都是增函数；在

在［2kπ-π，2kπ］

上都是增函数；

在［2kπ，2kπ+π］

上都是减函数

在(kπ-

2

π

，

在(kπ，kπ+π)内

都是减函数

(k∈Z)

y=secx的性质：

(1)定义域,{x|x≠π/2+kπ,k∈Z}

(2)值域,｜secx｜≥1．即secx≥1或secx≤－1;

(3)y=secx是偶函数，即sec(－x)=secx．图像对称于y轴;

(4)y=secx是周期函数．周期为2kπ(k∈Z，且k≠0)，最小正周期T=2π．

（5）正割与余弦互为倒数；余割与正弦互为倒数；

（6）正割函数无限趋于直线x=π/2+Kπ；

(7) 正割函数是无界函数；

（8）正割函数的导数：（secx）′=secx×tarx；

（9正割函数的不定积分：∫secxdx=ln∣secx+tanx∣+C

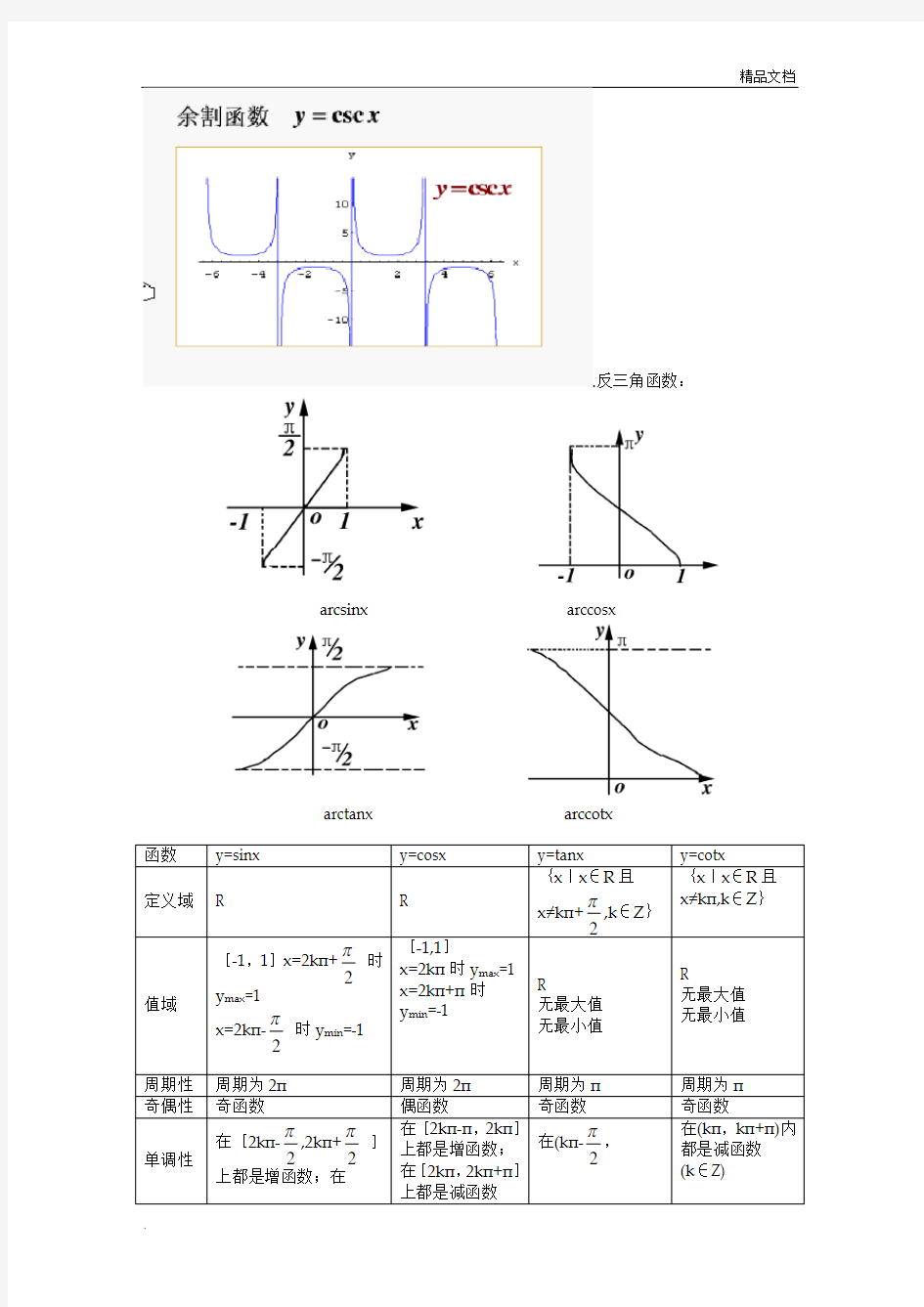
y=cscx的性

1、定义域：{x|x≠kπ，k∈Z}

2、值域：{y|y≤-1或y≥1}

3、奇偶性：奇函数

4、周期性：最小正周期为2π

5、图像：

图像渐近线为：x=kπ ，k∈Z 余割函数与正弦函数互为倒数第一部分三角函数公式

·两角和与差的三角函数

cos(α+β)=cosα·cosβ-sinα·sinβ

cos(α-β)=cosα·cosβ+sinα·sinβ

sin(α±β)=sinα·cosβ±cosα·sinβ

tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)

tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)

·和差化积[/url]公式：

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]

·积化和差[/url]公式：

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

·倍角公式[/url]：

sin(2α)=2sinα·cosα=2/(tanα+cotα)

cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2

tan(2α)=2tanα/(1-tan^2α)

cot(2α)=(cot^2α-1)/(2cotα)

sec(2α)=sec^2α/(1-tan^2α)

csc(2α)=1/2*secα·cscα

·三倍角公式：

sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)

cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)

tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)

cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)

·n倍角公式：

sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…

cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]：

sin(α/2)=±√((1-cosα)/2)

cos(α/2)=±√((1+cosα)/2)

tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα

cot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)

sec(α/2)=±√((2secα/(secα+1))

csc(α/2)=±√((2secα/(secα-1))

·辅助角公式：

Asinα+Bcosα=√(A^2+B^2)sin(α+φ）（tanφ=B/A）

Asinα+Bcosα=√(A^2+B^2)cos(α-φ）（tanφ=A/B）

·万能公式

sin(a)= (2tan(a/2))/(1+tan^2(a/2))

cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))

tan(a)= (2tan(a/2))/(1-tan^2(a/2))

·降幂公式

sin^2α=(1-cos(2α))/2=versin(2α)/2

cos^2α=(1+cos(2α))/2=covers(2α)/2

tan^2α=(1-cos(2α))/(1+cos(2α))

·三角和的三角函数：

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγ

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγ

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

·其它公式

·两角和与差的三角函数

cos(α+β)=cosα·cosβ-sinα·sinβ

cos(α-β)=cosα·cosβ+sinα·sinβ

sin(α±β)=sinα·cosβ±cosα·sinβ

tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)

tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)

=sinα/(1-cosα) ·和差化积[/url]公式：

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]

·积化和差[/url]公式：

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

·倍角公式[/url]：

sin(2α)=2sinα·cosα=2/(tanα+cotα)

cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2

tan(2α)=2tanα/(1-tan^2α)

cot(2α)=(cot^2α-1)/(2cotα)

sec(2α)=sec^2α/(1-tan^2α)

csc(2α)=1/2*secα·cscα

·三倍角公式：

sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)

cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)

tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)

cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)

·n倍角公式：

sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…

cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]：

sin(α/2)=±√((1-cosα)/2)

cos(α/2)=±√((1+cosα)/2)

tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα

cot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα

sec(α/2)=±√((2secα/(secα+1))

csc(α/2)=±√((2secα/(secα-1))

·辅助角公式：

Asinα+Bcosα=√(A^2+B^2)sin(α+φ）（tanφ=B/A）

Asinα+Bcosα=√(A^2+B^2)cos(α-φ）（tanφ=A/B）

·万能公式

sin(a)= (2tan(a/2))/(1+tan^2(a/2))

cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))

tan(a)= (2tan(a/2))/(1-tan^2(a/2))

·降幂公式

sin^2α=(1-cos(2α))/2=versin(2α)/2

cos^2α=(1+cos(2α))/2=covers(2α)/2

tan^2α=(1-cos(2α))/(1+cos(2α))

·三角和的三角函数：

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγ

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγ

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

·其它公式

1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2

csc(a)=1/sin(a) sec(a)=1/cos(a)

cos30=sin60

sin30tanα+cotα=2/sin2α

tanα-cotα=-2cot21+cos2α=2cos^2α

1-cos2α=2sin^2α

1+sinα=[sin(α/2)+cos(α/2)]^2

1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 csc(a)=1/sin(a) sec(a)=1/cos(a)

cos30=sin60

sin30=cos60

·推导公式

tanα+cotα=2/sin2α

tanα-cotα=-2cot2α

1+cos2α=2cos^2α

1-cos2α=2sin^2α

1+sinα=[sin(α/2)+cos(α/2)]^2