高中数学竞赛专题精讲9三角恒等式与三角不等式(含答案)

9三角恒等式与三角不等式

三角恒等变形，既要遵循代数式恒等变形的一般法则，又有三角所特有的规律.

三角恒等式包括绝对恒等式和条件恒等式两类。证明三角恒等式时，首先要观察已知与求证或所证恒等式等号两边三角式的繁简程度，以决定恒等变形的方向；其次要观察已知与求证或所证恒等式等号两边三角式的角、函数名称、次数以及结构的差别与联系，抓住其主要差异，选择恰当的公式对其进行恒等变形，从而逐步消除差异，统一形式，完成证明.“和差化积”、“积化和差”、“切割化弦”、“降次”等是我们常用的变形技巧。当然有时也

可以利用万能公式“弦化切割”，将题目转化为一个关于

tan

t=的代数恒等式的证明问题.

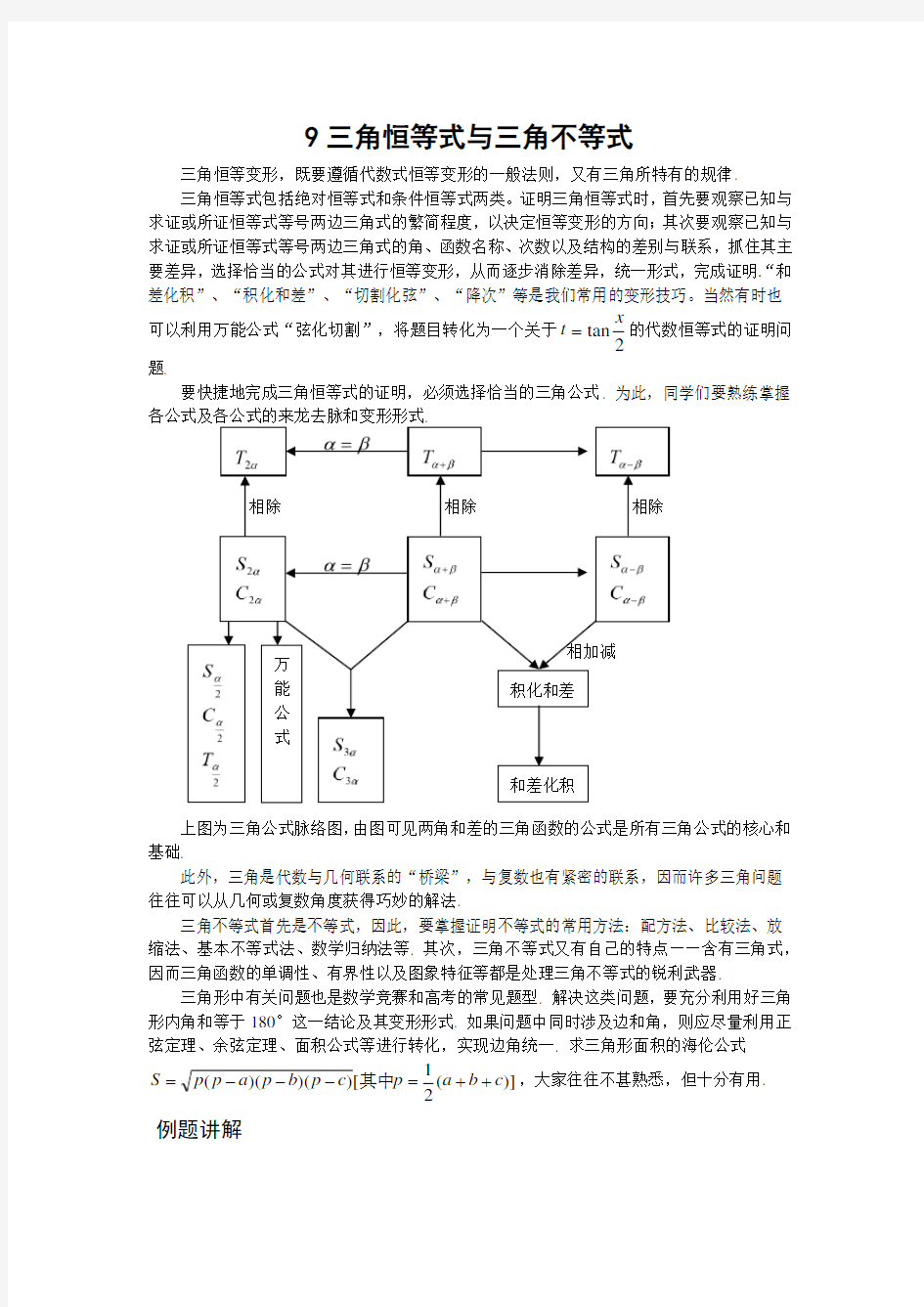
要快捷地完成三角恒等式的证明，必须选择恰当的三角公式. 为此，同学们要熟练掌握

上图为三角公式脉络图，由图可见两角和差的三角函数的公式是所有三角公式的核心和基础.

此外，三角是代数与几何联系的“桥梁”，与复数也有紧密的联系，因而许多三角问题往往可以从几何或复数角度获得巧妙的解法.

三角不等式首先是不等式，因此，要掌握证明不等式的常用方法：配方法、比较法、放缩法、基本不等式法、数学归纳法等. 其次，三角不等式又有自己的特点——含有三角式，因而三角函数的单调性、有界性以及图象特征等都是处理三角不等式的锐利武器.

三角形中有关问题也是数学竞赛和高考的常见题型. 解决这类问题，要充分利用好三角形内角和等于180°这一结论及其变形形式. 如果问题中同时涉及边和角，则应尽量利用正弦定理、余弦定理、面积公式等进行转化，实现边角统一. 求三角形面积的海伦公式

)]

(

[)

)(

S+

=其中，大家往往不甚熟悉，但十分有用.

例题讲解

万

能

公

式

相除相除相除

积化和差

和差化积

相加减

1．已知.cos sin )tan(:,1||),sin(sin A

A A -=

+>+=ββ

βαβαα求证

2．证明：.cos 64cos 353215cos 77cos 7x x x ocs x x =+++

3．求证：.112tan 312tan 18tan 18tan 3=++

4．已知.20012tan 2sec :,2001tan 1tan 1=+=-+ααα

α求证

5．证明：.3sin )60sin()60sin(sin 4θθθθ=+-

6．求证：①16

178cos 66cos 42cos 6cos = ②sin1°sin2°sin3°…sin89°=.106)

1(45

7．证明：对任一自然数n 及任意实数m n k m

x k ,,,2,1,0(2

=≠π为任一整数），有 .2cot cot 2sin 1

4sin 12sin 1x x x

x x n n

-=+++

8．证明：.2

sin

21sin )2sin()sin()2sin()sin(sin β

ββαβαβαβαα++

+++++++n n n

9．若πθ<<0，求证：03sin 3

2sin 21sin >++θθθ

10．已知πθ<<0，证明：2

2sin 2θ

θctg ≤，并讨论等号成立的条件。

11．已知)2

,0(,π

βα∈，能否以αsin ，βsin ，)sin(βα+的值为边长，构成三角形。

12．在△ABC 中，角A 、B 、C 的对边为a 、b 、c ，求证：3

≥++++c b a cC bB aA

13．在锐角△ABC 中，求证

（1）C B A C B A cos cos cos sin sin sin ++>++；（2）1>tgAtgBtgC

14．设12

≥

≥≥z y x ，且2

++z y x ，求乘积z y x cos sin cos 的最大值和最小值。

课后练习

1．证明：sin47°+sin61°－sin11°－sin25°=cos7°. 2．证明：

.sin sin )cos(2sin )2sin(α

βααβα=+-+

3．已知：sin A +sin B +sin C =0，cos A +cos B +cos C =0.

求证：sin2A +sin2B +sin2C =0，cos2A +cos2B +cos2C =0. 4．已知.03sin 3

2sin 21sin :),,0(=++∈θθθπθ求证 5．已知αβαβπ

βα-=<

<求且,tan 3tan ,2

0的最大值.

6．已知α、β、γ、θθγβαπθγβαπ

sin sin sin sin .),2,0(==+++∈y 求且的最大值. 7．△ABC 中，C=2B 的充要条件是.2

ab b c =-

8．△ABC 中，已知A 2

sin 、B 2

sin 、C 2

sin 成等差数列，求证：A cot 、B cot 、C cot 也成等差数列.

9．△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，已知c a b +=2，求B 的最大值. 10．若α、),2

,0(π

β∈能否以αsin 、βsin 、)sin(βα+的值为边长构成一个三角形.

11．求函数x x y 382-++=的值域.

12．求函数2212

2++++=

x x x

y 的值域. 13．在△ABC 中，求证：B b A a c cos cos +≥；A a C c b cos cos +≥；

A a

B b a cos cos +≥。

14．设α为锐角，求证：223)cos 11)(sin 11(+≥++

α 15．对)2

0(π

∈x ，求证：tgx x x +

例题答案：

１．分析：条件涉及到角α、βα+，而结论涉及到角βα+，β.故可利用

αβαβββαα-+=-+=)()(或消除条件与结论间角的差异，当然亦可从式中的“A ”

入手.

证法1： ),sin(sin βαα+=A

),sin()sin(βαββα+=-+∴A

cos(sin ))(cos sin(),sin(sin )cos(cos )sin(βαβββαβαββαββα+=-++=+-+A A

cos sin )tan(,

0)cos(,

0cos ,1||A

A A -=

+≠+≠-∴>ββ

βαβαβ从而

证法2：

αβαβββαβααββββ

sin )sin(cos sin )sin()

sin(sin cos sin sin sin -++=

-A

tan(sin )cos(sin )sin(])sin[()sin(cos sin )sin(βαββαβ

βαββαβαββ

βα+=++=-+-++=

２．分析：等号左边涉及角7x 、5x 、3x 、x 右边仅涉及角x ，可将左边各项逐步转化为x sin 、

x cos 的表达式，但相对较繁. 观察到右边的次数较高，可尝试降次.

证明：因为,cos 33cos cos 4,cos 3cos 43cos 3

x x x x x x +=-=所以从而有x x x x x 226cos 9cos 3cos 63cos cos 16++= =)2cos 1(2

)2cos 4(cos 326cos 1x x x x +++++

x x x x x x x x x x x x cos 20cos 2cos 30cos 4cos 12cos 6cos 2cos 64,

2cos 992cos 64cos 66cos 1cos 327

6+++=+++++=

cos 353cos 215cos 77cos cos 20cos 153cos 153cos 65cos 65cos 7cos x x x x x

x x x x x x +++=++++++=

评述：本题看似“化简为繁”，实质上抓住了降次这一关键，很是简捷. 另本题也可利用复

数求解. 令77)1

(cos 128,,1cos 2,sin cos z

z z z i z +=+

=+=αααα从而则，展开即可. ３．思路分析：等式左边同时出现 12tan 18tan 、 12tan 18tan +，联想到公式

αβ

αβαtan tan 1tan tan )tan(-+=

证明： 12tan 312tan 18tan 18tan 3++

12tan 18tan )12tan 18tan 1)(1218tan(312tan 18tan )12tan 18(tan 3=+-+?=++=

评述：本题方法具有一定的普遍性. 仿此可证)43tan 1()2tan 1)(1tan 1(

+++

222)44tan 1(=+ 等.、

４．证明：)4tan()

sin()

22cos(12cos 2sin 12tan 2sec απαπαπ

αααα+=++-=+=+

.2001tan 1tan 1=-+=

αα ５．证明：θθθ3sin 4sin 33sin -=

)

60sin()60sin(sin 4)

sin 60cos cos 60)(sin sin 60cos cos 60(sin sin 4])sin 2

1()cos 23[(sin 4)

sin 4

cos 43(sin 4)

sin 43

(sin 422222θθθθθθθθθθθθθθθθ-+=-+=-=-=-=

评述：这是三倍角的正弦的又一表示. 类似地，有)60cos()60cos(cos 43cos θθθθ+-=

)60tan()60tan(tan 3tan θθθθ+-+= . 利用这几个公式可解下例.

6. 证明：①cos6°cos42°cos66°cos78°

=cos6°cos54°cos66°

54cos 78cos 42cos ?

.16

154cos 4)

183cos(41

54cos 478cos 42cos 18cos =?==

②sin1°sin2°sin3°…sin89°

=(sin1°sin59°sin61°)(sin2°sin58°sin62°)…(sin29°sin31°sin89°)sin30°sin60° =4

387sin 6sin 3sin )

1(29

60sin 30sin )87sin 33sin 27(sin )66sin 54sin 6)(sin 63sin 57sin 3(sin 3)4

(30=

45sin )54sin 36)(sin 63sin 27)(sin 72sin 18)(sin 18sin 9(sin 3)4

(81sin 18sin 9sin 3)41

(4040???=??=

36sin 18cos 22

3)41(54cos 72sin 223)41(54cos 18sin 36cos 18cos 223)41(54cos 72cos 36cos 18cos 223)41(18cos 36cos 54cos 72cos 223)41(72sin 54sin 36sin 18sin 223)41(434342424242?=?=?=?=?=?= 又)72cos 1)(36cos 1(4

)36sin 18(cos 2 -+=

5)72cos 36cos 1(41)72cos 36cos 72cos 36cos 1(4

=+=--+=

即 .4

536sin 18cos =

所以 .106)4

1(89sin 2sin 1sin 45?=

7. 思路分析：本题左边为n 项的和，右边为2项之差，故尝试将左边各项“裂”成两项之

差，并希冀能消去其中许多中间项.

证明：,2cot cot 2sin 2cos cos sin 2cos 22sin 2cos cos 22sin 122x x x

x x x x x x x -=-=-=

同理x x x 4cot 2cot 4sin 1

……

x x x

n n n

2cot 2cot 2sin 1

1-=- 评述：①本题裂项技巧也可通过数学归纳法获得.

②“裂项相消”在解题中具有一定的普遍性，类似可证下列各题：

n n n n -=

-+++α

ααααααtan tan tan )1tan(3tan 2tan 2tan tan .

cot 1cos 89cos 88cos 12cos 1cos 11cos 0cos 1.2cot 2cot 2tan 22tan 22tan 2tan 1122=+++-=++++++ααααααn n n n

8. 证明：)],2

cos()2[cos(212sin

sin β

αβαβ

α--+-=

)]

sin()2sin()sin([sin 2

sin

)]2

2cos()212[cos(212sin )sin(,

)]2

cos()25[cos(212sin )2sin()],2cos()23[cos(212sin

)sin(βαβαβααβ

βαβαββαβαβαββαβ

αβαβ

βαn n n n +++++++-+-++-=++-+-=++-+-=+

各项相加得类似地

sin )2sin()]

2cos()212[cos(21ββαβ

αβα++=--++-=n n n

所以，.2

sin

sin )2sin()sin()sin(sin β

ββαβαβαα++

+++++n n n 评述：①本题也可借助复数获证.

②类似地，有.2

sin

)2cos(21sin

)cos()cos(cos β

βαββαβααn

n n ++=

+++++

利用上述公式可快速证明下列各式：

sin 21

cos 2sin cos 3cos 2cos cos θθθθθθθ+=

++++n n n

2197cos 95cos 93cos 9cos .2

175cos 73cos 9cos

等=+++=++πππππππ

全国高中数学竞赛专题-不等式

全国高中数学竞赛专题-不等式证明不等式就是对不等式的左右两边或条件与结论进行代数变形和化归，而变形的依据是不等式的性质，不等式的性质分类罗列如下：不等式的性质：.0,0<-?<>-?≥b a b a b a b a 这是不等式的定义，也是比较法的依据. 对一个不等式进行变形的性质：（1）a b b a （对称性）（2）c b c a b a +>+?>（加法保序性）（3）.0,;0,bc ac c b a bc ac c b a >?>> （4）*).(,0N n b a b a b a n n n n ∈>>?>> 对两个以上不等式进行运算的性质. （1）c a c b b a >?>>,（传递性）.这是放缩法的依据. （2）.,d b c a d c b a +>+?>> （3）.,d b c a d c b a ->-?<> （4）.,,0,0bc ad d b c a c d b a >>?>>>> 含绝对值不等式的性质：（1）.)0(||22a x a a x a a x ≤≤-?≤?>≤ （2）.)0(||22a x a x a x a a x -≤≥?≥?>≥或（3）||||||||||||b a b a b a +≤±≤-（三角不等式）. （4）.||||||||2121n n a a a a a a +++≤+++ 证明不等式的常用方法有：比较法、放缩法、变量代换法、反证法、数学归纳法、构造函数方法等.当然在证题过程中，常可“由因导果”或“执果索因”.前者我们称之为综合法；后者称为分析法.综合法和分析法是解决一切数学问题的常用策略，分析问题时，我们往往用分析法，而整理结果时多用综合法，这两者并非证明不等式的特有方法，只是在不等式证明中使用得更为突出而已.此外，具体地证明一个不等式时，可能交替使用多种方法.因此，要熟练掌握不等式的证明技巧，必须从学习这些基本的常用方法开始。 1．比较法（比较法可分为差值比较法和商值比较法。）（1）差值比较法（原理：A － B ＞0 A ＞ B ．）例1 设a, b, c ∈R +，

高中数学奥赛讲义：竞赛中常用的重要不等式

不等式是数学竞赛的热点之一。由于不等式的证明难度大，灵活性强，要求很高的技巧，常常使它成为各类数学竞赛中的“高档”试题。而且，不论是几何、数论、函数或组合数学中的许多问题，都可能与不等式有关，这就使得不等式的问题（特别是有关不等式的证明）在数学竞赛中显得尤为重要。证明不等式同大多数高难度的数学竞赛问题一样，没有固定的模式，证法因题而异，灵活多变，技巧性强。但它也有一些基本的常用方法，要熟练掌握不等式的证明技巧，必须从学习这些基本的常用方法开始。竞赛中常用的重要不等式【内容综述】本讲重点介绍柯西不等式、排序不等式、切比雪夫不等式的证明与应用【要点讲解】目录§1 柯西不等式 §2 排序不等式 §3 切比雪夫不等式 ★ ★ ★ §1。柯西不等式定理1 对任意实数组恒有不等式“积和方不大于方和积”，即等式当且仅当时成立。本不等式称为柯西不等式。思路一证不等式最基本的方法是作差比较法，柯西不等式的证明也可首选此法。证明1 ∴右-左= 当且仅当定值时，等式成立。思路2 注意到时不等式显然成立，当时，不等式左、右皆正，因此可考虑作商比较法。

证明2 当时等式成立；当时，注意到 =1 故当且仅当且（两次放缩等式成立条件要一致）

即同号且常数，亦即思路3 根据柯西不等式结构，也可利用构造二次函数来证明。证明3 构造函数。由于恒非负，故其判别式即有等式当且仅当常数时成立。若柯西不等式显然成立。例1 证明均值不等式链：调和平均数≤算术平均数≤均方平均数。证设本题即是欲证：本题证法很多，现在我们介绍一种主要利用柯西不等式平证明的方法 (1)先证① 注意到欲证①,即需证 ② 此即由柯西不等式,易知②成立,从而①真

高中数学必修四第三章-三角恒等变换知识点总结

第三章三角恒等变换一、两角和与差的正弦、余弦和正切公式： ⑴()cos cos cos sin sin αβαβαβ-=+； ⑵()cos cos cos sin sin αβαβαβ+=-； ⑶()sin sin cos cos sin αβαβαβ-=-； ⑷()sin sin cos cos sin αβαβαβ+=+； ⑸()tan tan tan 1tan tan αβ αβαβ --= + ? ()()tan tan tan 1tan tan αβαβαβ-=-+ ⑹()tan tan tan 1tan tan αβ αβαβ ++=- ? ()()tan tan tan 1tan tan αβαβαβ+=+- 二、二倍角的正弦、余弦和正切公式： sin 22sin cos ααα =222)cos (sin cos sin 2cos sin 2sin 1ααααααα±=±+=±? ⑵2222cos2cos sin 2cos 112sin α αααα=-=-=- ?2 2 1cos 2cos 1cos 2sin 2 2 α α αα+=-=， ?2 cos 21cos 2 αα+= ，2 1cos 2sin 2αα-=． ⑶22tan tan 21tan α αα =-．三、辅助角公式： () 22sin cos sin α+=++a x b x a b x ， 2 2 2 2 cos sin a b a b a b ???= = ++其中由，决定

四、三角变换方法：（1）角的变换：在三角化简，求值，证明中，表达式中往往出现较多的相异角，可根据角与角之间的和差，倍半，互补，互余的关系，运用角的变换，沟通条件与结论中角的差异，使问题获解，对角的变形如： ①α2是α的二倍；α4是α2的二倍；α是2α的二倍；2α是4 α的二倍； ②2 304560304515o o o o o o =-=-=； ③()ααββ=+-；④ ()4 24 π π π αα+= --； ⑤2()()()()44 ππ ααβαβαα=++-=+--；等等（2）函数名称变换：三角变形中，常常需要变函数名称为同名函数。如在三角函数中正余弦是基础，通常化切为弦，变异名为同名。（3）“1”的代换：在三角函数运算，求值，证明中，有时需要将常数转化为三角函数值，例如常数“1”的代换变形有： 221sin cos sin90tan45o o αα=+== （4）幂的变换：降幂是三角变换时常用方法，对次数较高的三角函数式，一般采用降幂处理的方法。降幂并非绝对，有时需要升幂，如对无理式αcos 1+常用升幂化为有理式。（5）三角函数式的变换通常从：“角、名、形、幂”四方面入手；基本原则是：见切化弦，异角化同角，倍角化单角，异名化同名，高次降低次，特殊值与特殊角的三角函数互化等。

高中数学竞赛_集合函数不等式导数

专题二集合函数不等式导数一能力培养 1,函数与方程思想; 2,数形结合思想; 3,分类讨论思想; 4,运算能力; 5,转化能力. 二问题探讨 [问题1] 已知{3}A x x a =-≤,2{780}B x x x =+->,分别就下面条件求a 的取值范围: (I)A B =?;(II)A B B =. [问题2]求函数()a f x x x =+ 的单调区间,并给予证明. [问题3]已知()1x f x e ax =--. (I)若()f x 在定义域R 内单调递增,求a 的取值范围; (II)若()f x 在(,0]-∞上单调递减,在[0,)+∞上单调递增,求a 的值; (III)设2()22g x x x =-++在(II)的条件下,求证()g x 的图象恒在()f x 图象的下方. [问题4]设11()lg 21x f x x x -=+++. (I)试判断()f x 的单调性; (II)若()f x 的反函数为1()f x -,证明1()0f x -=只有一个解; (III)解关于x 的不等式1 1[()]22 f x x -<.

三习题探讨选择题 1已知函数()2x f x =,则12(4)f x --的单调减区间是 A,[0,)+∞ B,(,0]-∞ C,[0,2) D,(2,0]- 2已知集合M={01}x x ≤≤,N={01}x x ≤≤,下列法则不能构成M 到N 的映射的是 A,2y x = B,sin y x = C,tan y x = D,y 3已知函数(1)()(1)x x f x x x ≥?=?-?,已知()1f a >,则a 的取值范围为 A,(1,1)- B,(,1)(1,)-∞-+∞ C,(,2)(0,)-∞-+∞ D,(1,)+∞ 6对于函数32()3f x x x =-,有下列命题:①()f x 是增函数,无极值;②()f x 是减函数, 无极值;③()f x 的增区间是(,0)-∞,(2,)+∞,()f x 的减区间是(0,2);④(0)0f =是极大值,(2)4f =-是极小值.其中正确的命题有 A,一个 B,二个 C,三个 D,四个填空题 7函数2(2)log x f x =的定义域是 . 8已知2(1cos )sin f x x -=,则()f x = . 9函数2log (252)x y x x =-+-单调递增区间是 . 10若不等式2log 0(0,1)a x x a a -<>≠对满足102 x <<的x 恒成立,则实数

高中数学竞赛解题方法篇(不等式)

高中数学竞赛中不等式的解法摘要：本文给出了竞赛数学中常用的排序不等式，平均值不等式，柯西不等式和切比雪夫不等式的证明过程，并挑选了一些与这几类不等式相关的一些竞赛题进行了分析和讲解。希望对广大喜爱竞赛数学的师生有所帮助。不等式在数学中占有重要的地位，由于其证明的困难性和方法的多样性，而成为竞赛数学中的热门题型.在解决竞赛数学中的不等式问题的过程中，常常要用到几个著名的代数不等式：排序不等式、平均值不等式、柯西不等式、切比雪夫不等式.本文就将探讨这几个不等式的证明和它们的一些应用. 1．排序不等式定理1 设1212...,...n n a a a b b b ≤≤≤≤≤≤，则有 1211...n n n a b a b a b -+++ (倒序积和) 1212...n r r n r a b a b a b ≤+++（乱序积和） 1122 ...n n a b a b a b ≤+++（顺序积和）其中1,2,...,n r r r 是实数组1,2,...,n b b b 一个排列，等式当且仅当12...n a a a ===或 12...n b b b ===时成立.

（说明：本不等式称排序不等式，俗称倒序积和乱序积和顺序积和.）证明：考察右边不等式，并记1 2 12...n r r n r S a b a b a b =+++。不等式 1 2 12...n r r n r S a b a b a b ≤+++的意义：当121,2,...,n r r r n ===时，S 达到最大值1122 ...n n a b a b a b +++.因此，首先证明n a 必须和n b 搭配，才能使S 达到最大值.也即，设n r n <且n b 和某个()k a k n <搭配时有 .n n k n n r k r n n a b a b a b a b +≤+ （1-1）事实上， ()()()0n n n n n k r k n n r n r n k a b a b a b a b b b a a +-+=--≥ 不等式（1-1）告诉我们当n r n <时，调换n b 和n r b 的位置（其余n-2项不变），会使和S 增加.同理，调整好n a 和n b 后，再调整1n a -和1n b -会使和增加.经过n 次调整后，和S 达到最大值1122 ...n n a b a b a b +++，这就证明了 1212...n r r n r a b a b a b +++1122 ...n n a b a b a b ≤+++. 再证不等式左端, 由1211...,...n n n a a a b b b -≤≤≤-≤-≤≤-及已证明的不等式右端，得 1211(...)n n n a b a b a b --+++1212(...)n r r n r a b a b a b ≥-+++

高中数学人教版必修简单的三角恒等变换教案(系列一)

3.2 简单的三角恒等变换一．教学目标 1、通过二倍角的变形公式推导半角的正弦、余弦、正切公式，体会化归、换元、方程、逆向使用公式等数学思想，提高学生的推理能力。 2、理解并掌握二倍角的正弦、余弦、正切公式，并会利用公式进行简单的恒等变形，体会三角恒等变形在数学中的应用。 3、通过例题的解答，引导学生对变换对象目标进行对比、分析，促使学生形成对解题过程中如何选择公式，如何根据问题的条件进行公式变形，以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识，从而加深理解变换思想，提高学生的推理能力．二、教学重点与难点教学重点：引导学生以已有的十一个公式为依据，以推导积化和差、和差化积、半角公式的推导作为基本训练，学习三角变换的内容、思路和方法，在与代数变换相比较中，体会三角变换的特点，提高推理、运算能力．教学难点：认识三角变换的特点，并能运用数学思想方法指导变换过程的设计，不断提高从整体上把握变换过程的能力．三、教学设想：（一）复习：三角函数的和（差）公式，倍角公式（二）新课讲授： 1、由二倍角公式引导学生思考：2 αα与有什么样的关系？学习和（差）公式，倍角公式以后，我们就有了进行变换的性工具，从而使三角变换的内容、思路和方法更加丰富，这为我们的推理、运算能力提供了新的平台．例1、试以cos α表示222 sin ,cos ,tan 222α α α．解：我们可以通过二倍角2cos 2cos 12αα=-和2cos 12sin 2αα=-来做此题．因为2cos 12sin 2αα=-，可以得到21cos sin 2 2α α-=；

因为2cos 2cos 12α α=-，可以得到21cos cos 22 α α+=．又因为222 sin 1cos 2tan 21cos cos 2α α ααα-==+．思考：代数式变换与三角变换有什么不同？代数式变换往往着眼于式子结构形式的变换．对于三角变换，由于不同的三角函数式不仅会有结构形式方面的差异，而且还会有所包含的角，以及这些角的三角函数种类方面的差异，因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系，这是三角式恒等变换的重要特点．例2．已知135sin = α，且α在第二象限，求2tan α的值。例3、求证：（１）、()()1sin cos sin sin 2 αβαβαβ=++-????；（２）、sin sin 2sin cos 22θ? θ? θ?+-+=．证明：（１）因为()sin αβ+和()sin αβ-是我们所学习过的知识，因此我们从等式右边着手． ()sin sin cos cos sin αβαβαβ+=+；()sin sin cos cos sin αβαβαβ-=-．两式相加得()()2sin cos sin sin αβαβαβ=++-；即()()1sin cos sin sin 2 αβαβαβ=++-????；（２）由（１）得()()sin sin 2sin cos αβαβαβ++-=①；设,αβθαβ?+=-=，那么,22θ? θ? αβ+-==．把,αβ的值代入①式中得sin sin 2sin cos 22θ?θ?θ?+-+=．思考：在例3证明中用到哪些数学思想？例3证明中用到换元思想，（１）式是积化和差的形式，

初中数学竞赛专题：不等式

初中数学竞赛专题：不等式 §5.1 一元一次不等式（组） 5.1.1★已知2(2)3(41)9(1)x x x ---=-,且9y x <+,试比较1π y 与 10 31 y 的大小. 解析首先解关于x 的方程得10x =-.将10x =-代入不等式得109y <-+,即1y <-.又因为110π 31 <,所以110π 31 y y > 5.1.2★解关于x 的不等式 233122x x a a +--> . 解析由题设知0a ≠,去分母并整理得 (23)(23)(1)a x a a +>+-. 当230a +>,即3 (0)2 a a >-≠时,1x a >-；当230a +=,即32 a =-时,无解；当230a +<,即32 a <-时,1x a <-. 评注对含有字母系数的不等式的解,也要分情况讨论. 5.1.3★★已知不等式(2)340a b x a b -+-<的解为49 x >,求不等式(4)230a b x a b -+->的解. 解析已知不等式为(3)43a b x b a -<-.由题设知 20, 434.29a b b a a b -等价于 721 ()2028 a a x a a -+->, 即5528ax a ->,解得14 x >-. 所求的不等式解为14 x >-.

5.1.4★★如果关于x 的不等式 (2)50a b x a b -+-> 的解集为10 7 x < ,求关于x 的不等式ax b >的解集. 解析由已知得 (2)5a b x b a ->-,① 710x ->-.② 由已知①和②的解集相同,所以 27, 510, a b b a -=-?? -=-? 解得 5, 3. a b =-?? =-? 从而ax b >的解集是3 5 x <. 5.1.5★求不等式 111 (1)(1)(2)326 x x x +---≥ 的正整数解. 解析由原不等式可得1736x ≤,所以72 x ≤是原不等式的解.因为要求正整数解,所以原不等式的正整数解为1x =,2,3. 5.1.6★★如果不等式组90, 80x a x b -?? -

人教版高中数学必修四三角恒等变换题库

（数学4必修）第三章三角恒等变换 [基础训练A 组] 一、选择题 1．已知(,0)2x π∈-，4cos 5x =，则=x 2tan （） A ．247 B ．247- C ．724 D ．7 24- 2．函数3sin 4cos 5y x x =++的最小正周期是（） A . 5π B .2 π C .π D .2π 3．在△ABC 中，cos cos sin sin A B A B >，则△ABC 为（） A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．无法判定 4．设00sin14cos14a =+，00sin16cos16b =+，c = ，则,,a b c 大小关系（） A ．a b c << B ．b a c << C ．c b a << D ．a c b << 5．函数)cos[2()]y x x ππ= -+是（） A .周期为4π的奇函数 B .周期为4 π的偶函数 C .周期为2π的奇函数 D .周期为2 π的偶函数 6．已知cos 2θ= 44sin cos θθ+的值为（） A ．1813 B ．1811 C ．9 7 D ．1- 二、填空题 1．求值：0000 tan 20tan 4020tan 40+=_____________。 2．若1tan 2008,1tan αα+=-则1tan 2cos 2αα += 。 3．函数f x x x x ()cos sin cos =-223的最小正周期是___________。

4．已知sin cos 223 θ θ +=那么sin θ的值为 ,cos2θ的值为。 5．ABC ?的三个内角为A 、B 、C ，当A 为时，cos 2cos 2 B C A ++取得最大值，且这个最大值为。三、解答题 1．已知sin sin sin 0,cos cos cos 0,αβγαβγ++=++=求cos()βγ-的值. 2．若,2 2sin sin = +βα求βαcos cos +的取值范围。 3．求值：0 010001cos 20sin10(tan 5tan 5)2sin 20 -+-- 4．已知函数.,2 cos 32sin R x x x y ∈+= （1）求y 取最大值时相应的x 的集合；（2）该函数的图象经过怎样的平移和伸变换可以得到)(sin R x x y ∈=的图象. （数学4必修）第三章三角恒等变换 [综合训练B 组] 一、选择题 1．设2132tan131cos50cos6sin 6,,,221tan 13a b c -=-==+则有（） A .a b c >> B .a b c << C .a c b << D .b c a <<

高中数学竞赛均值不等式讲义

均值不等式 1.均值不等式知识点1: 二元均值不等式可以推广到n 元，即：设,,, 123 a a a a n 为n 个非负实数，则 12n a a a n ++ + ≥1 23 a a a a n === =）. 如何证明? 知识点2: 设,,, 123 a a a a n 为n 个非负实数 ,n Q , 12n n a a a A n ++ += , n G =, 12 111n n n H a a a = ++,则n n n n Q A G H ≥≥≥(等号成立当且仅当 123a a a a n ====) 更一般的平均值的定义: 设正数(1,2,3...)i a i n =,则α的幂平均值=1 1 ( )n i i a n α α =∑,特别的,我们有: lim ()n f G αα→=，1 1 ()( )n i i a f n α α α==∑为关于α的增函数. 知识点3:重要结论 (1)2 22,,,.a b c R a b c ab bc ac ∈++≥++ (2) ()2 ,,,3().a b c R a b c ab bc ac ∈++≥++ (3) 2222,,,3()().a b c R a b c a b c ∈++≥++ (4) 2,,,()3().a b c R ab bc ca abc a b c ∈++≥++ (5) ,,,()()()()().a b c R a b b c a c abc a b c ab cb ac ∈++++=++++ (6) 222;2a a a b b a b b -≥-+≥(a,b,c>0) (7) 2222221 ()()3 a b b c c a a b c a b c ++≤++++(a,b,c>0) (8)正实数(1,2,3...)i a i n =,则 21 1 1 n n i i i i a n a ==?≥∑∑ (当且仅当12...n a a a ===); (9) 222222222222()()()()()a b b c c a ab bc ca a b c a bc b ca c ab ++++=++++ 知识点4:加权平均值不等式已知 12+...1(0,1,2.,,,) n i w w w w i n +=>=，则对任意正实数 12112212........n w w w n n n w a w a w a a a a +++≥.

高中数学竞赛解题方法篇不等式

高中数学竞赛解题方法篇不等式 The pony was revised in January 2021

高中数学竞赛中不等式的解法摘要：本文给出了竞赛数学中常用的排序不等式，平均值不等式，柯西不等式和切比雪夫不等式的证明过程，并挑选了一些与这几类不等式相关的一些竞赛题进行了分析和讲解。希望对广大喜爱竞赛数学的师生有所帮助。不等式在数学中占有重要的地位，由于其证明的困难性和方法的多样性，而成为竞赛数学中的热门题型.在解决竞赛数学中的不等式问题的过程中，常常要用到几个着名的代数不等式：排序不等式、平均值不等式、柯西不等式、切比雪夫不等式.本文就将探讨这几个不等式的证明和它们的一些应用. 1．排序不等式定理1 设1212...,...n n a a a b b b ≤≤≤≤≤≤，则有 1211...n n n a b a b a b -+++(倒序积和) 1212...n r r n r a b a b a b ≤+++（乱序积和） 1122 ...n n a b a b a b ≤+++（顺序积和）其中1,2,...,n r r r 是实数组1,2,...,n b b b 一个排列，等式当且仅当12...n a a a ===或 12...n b b b ===时成立. （说明：本不等式称排序不等式，俗称倒序积和乱序积和顺序积和.）证明：考察右边不等式，并记1212...n r r n r S a b a b a b =+++。

不等式1212...n r r n r S a b a b a b ≤+++的意义：当121,2,...,n r r r n ===时，S 达到最大值 1122 ...n n a b a b a b +++.因此，首先证明n a 必须和n b 搭配，才能使S 达到最大值.也即，设n r n <且n b 和某个()k a k n <搭配时有 .n n k n n r k r n n a b a b a b a b +≤+（1-1）事实上，不等式（1-1）告诉我们当n r n <时，调换n b 和n r b 的位置（其余n-2项不变），会使和S 增加.同理，调整好n a 和n b 后，再调整1n a -和1n b -会使和增加.经过n 次调整后，和S 达到最大值1122 ...n n a b a b a b +++，这就证明了1212...n r r n r a b a b a b +++1122 ...n n a b a b a b ≤+++. 再证不等式左端, 由1211...,...n n n a a a b b b -≤≤≤-≤-≤≤-及已证明的不等式右端，得即1211...n n n a b a b a b -+++1212...n r r n r a b a b a b ≤+++. 例1（美国第3届中学生数学竞赛题）设a,b,c 是正数，求证：3 ()a b c a b c a b c abc ++≥. 思路分析：考虑两边取常用对数，再利用排序不等式证明. 证明：不妨设a b c ≥≥，则有lg lg lg a b c ≥≥ 根据排序不等式有：以上两式相加，两边再分别加上lg lg lg a a b b c c ++

数学竞赛选讲不等式证明

§14不等式的证明不等式在数学中占有重要地位，由于其证明的困难性和方法的多样性，而成为竞赛和高考的热门题型. 证明不等式就是对不等式的左右两边或条件与结论进行代数变形和化归，而变形的依据是不等式的性质，不等式的性分类罗列如下：不等式的性质：.0,0<-?<>-?≥b a b a b a b a 这是不等式的定义，也是比较法的依据. 对一个不等式进行变形的性质：（1）a b b a （对称性）（2）c b c a b a +>+?>（加法保序性）（3）.0,;0,bc ac c b a bc ac c b a >?>> （4）*).(,0N n b a b a b a n n n n ∈> >?>> 对两个以上不等式进行运算的性质. （1）c a c b b a >?>>,（传递性）.这是放缩法的依据. （2）.,d b c a d c b a +>+?>> （3）.,d b c a d c b a ->-?<> （4）.,,0,0bc ad d b c a c d b a >>?>>>> 含绝对值不等式的性质：（1）.)0(||2 2 a x a a x a a x ≤≤-?≤?>≤ （2）.)0(||2 2 a x a x a x a a x -≤≥?≥?>≥或（3）|||||||||||| b a b a b a +≤±≤-（三角不等式）. （4）.||||||||2121n n a a a a a a +++≤+++ΛΛ 证明不等式的常用方法有：比较法、放缩法、变量代换法、反证法、数学归纳法、构造函数方法等.当然在证题过程中，常可“由因导果”或“执果索因”.前者我们称之为综合法；后者称为分析法.综合法和分析法是解决一切数学问题的常用策略，分析问题时，我们往往用分析法，而整理结果时多用综合法，这两者并非证明不等式的特有方法，只是在不等式证明中使用得更为突出而已.此外，具体地证明一个不等式时，可能交替使用多种方法. 例题讲解 1．,0,,>c b a 求证：.6)()()(abc a c ca c b bc b a ab ≥+++++ 2．0,,>c b a ，求证：.) (3 c b a c b a ab c c b a ++≥ 3．：.222,,,3 33222222ab c ca b bc a b a c a c b c b a c b a R c b a ++≤+++++≤ ++∈+ 求证 4．设* 21,,,N a a a n ∈Λ，且各不相同，求证：.321312112 23221n a a a a n n ++++≤+ +++ΛΛ.

【数学竞赛各阶段书籍推荐】

金牌学生推荐（可参照选择）一、第零阶段：知识拓展《数学选修4-1：几何证明选讲》《数学选修4-5：不等式选讲》《数学选修4-6：初等数论初步》二、全国高中数学联赛各省赛区预赛（即省选初赛） 1、《五年高考三年模拟》B版或《3年高考2年模拟》第二轮复习专用 2、《高中数学联赛备考手册》华东师范大学出版社（推荐指数五颗星） 3、《奥赛经典：超级训练系列》高中数学沈文选主编湖南师范大学出版社（推荐指数五颗星） 4、单樽《解题研究》（推荐指数五颗星） 5、单樽《平面几何中的小花》（个别地区竞赛会考到平几） 6、《平面几何》浙江大学出版社 7、奥林匹克小丛书第二版《不等式的解题方法与技巧》苏勇熊斌著三、第二阶段：全国高中数学联赛一试 0、《奥林匹克数学中的真题分析》沈文选湖南师范大学出版社（推荐指数五颗星） 1、《高中数学联赛考前辅导》熊斌冯志刚华东师范大学出版社 2、《数学竞赛培优教程（一试）》浙江大学出版社 3、命题人讲座《数列与数学归纳法》单樽 4、《数列与数学归纳法》（小丛书第二版，冯志刚） 5、《数列与归纳法》浙江大学出版社韦吉珠 6、《解析几何的技巧》单樽（建议买华东师大出版的版本） 7、《概率与期望》单樽 8、《同中学生谈排列组合》苏淳 9、《函数与函数方程》奥林匹克小丛书第二版 10、《三角函数》奥林匹克小丛书第二版 11、《奥林匹克数学中的几何问题》沈文选（推荐指数五颗星） 12、《圆锥曲线的几何性质》 13、《解析几何》浙江大学出版社二试平几 1、高中数学竞赛解题策略(几何分册)沈文选（推荐指数五颗星）

2、《奥林匹克数学中的几何问题》沈文选（推荐指数五颗星） 3、奥林匹克小丛书第二版《平面几何》 4、浙大小红皮《平面几何》 5、沈文选《三角形的五心》 6、田廷彦《三角与几何》 7、田廷彦《面积与面积方法》不等式 8、《初等不等式的证明方法》韩神 9、命题人讲座《代数不等式》计神 10、《重要不等式》中科大出版社 11、奥林匹克小丛书《柯西不等式与平均值不等式》数论（9,10，11选一本即可，某位大神说二试改为四道题以来没出过难题） 12、奥林匹克小丛书初中版《整除，同余与不定方程》 13、奥林匹克小丛书《数论》 14、命题人讲座《初等数论》冯志刚组合 15、奥林匹克小丛书第二版《组合数学》 16、奥林匹克小丛书第二版《组合几何》 17、命题人讲座刘培杰《组合问题》 18、《构造法解题》余红兵 19、《从特殊性看问题》中科大出版社 20、《抽屉原则》常庚哲四、中国数学奥林匹克（Chinese Mathematical Olympiad）及以上命题人讲座《圆》田廷彦《近代欧式几何学》《近代的三角形的几何学》《不等式的秘密》范建熊、隋振林《奥赛经典：奥林匹克数学中的数论问题》沈文选《奥赛经典：数学奥林匹克高级教程》叶军《初等数论难题集》命题人讲座《图论》奥林匹克小丛书第二版《图论》《走向IMO》