数学物理方法考题汇总

第一章 一维波动方程的付氏解

一．简述偏微分方程，阶，线性非线性，齐次非齐次的概念

答：（1）含有未知函数关于自变量的偏导数的等式称为偏微分方程，简称PDE(Partial Differential Equation)

（2）偏微分方程的阶：出现在偏微分方程中未知函数偏导数的最大阶数。

（3）方程中各项关于未知函数及其各阶偏导数都是一次的，称为线性；否则称为非线性方程。

（4）不含有未知函数及其偏导数的项称为自由项，自由项为零的方程称为齐次方程，否则称为非齐次方程。

二．P24(8) 指出下列微分方程的阶、线性、齐次性：

①(Tricomi 方程): 0xx yy yu u += （2阶线性齐次）

②(Klein-Gordon 方程): 22

0tt u y u c u -?+=（2阶线性齐次）

③(激波方程): 0t x u uu += （1阶非线性齐次） ④(KdV 方程 ): 60t x xxx u uu u -+= （3阶非线性齐次）

⑤(多空介质方程): m

t u k u =? （2阶非线性齐次）

三．简述二阶线性偏微分方程的分类方法，P24(9) 对方程111222122+++++=xx

xy yy x y a u a u a u b u b u cu f

2

1211220 ()=0 ()<(Laplace,Poisson)a a a >???≡-???

双曲型弦振动抛物型热传导0 椭圆型

（1）43260+-++=xx xy yy x y u u u u u ：双曲线型

（2）22

(1)(1)0+++++=xx yy x y x u y u xu yu ：椭圆型

四．何谓发展方程？何谓位势方程？何谓叠加原理？

(1) 发展方程: 所描述的物理过程随时间而演变,如:波动方程、

热传导方程等；

(2) 位势方程：所描述的自然现象是稳恒的，即与时间无关，

如：静电场、引力场等。

(3) 几种不同原因综合产生的效果等于这些原因单独产生效果

的累加.叠加原理适用于线性方程所描述的物理现象.

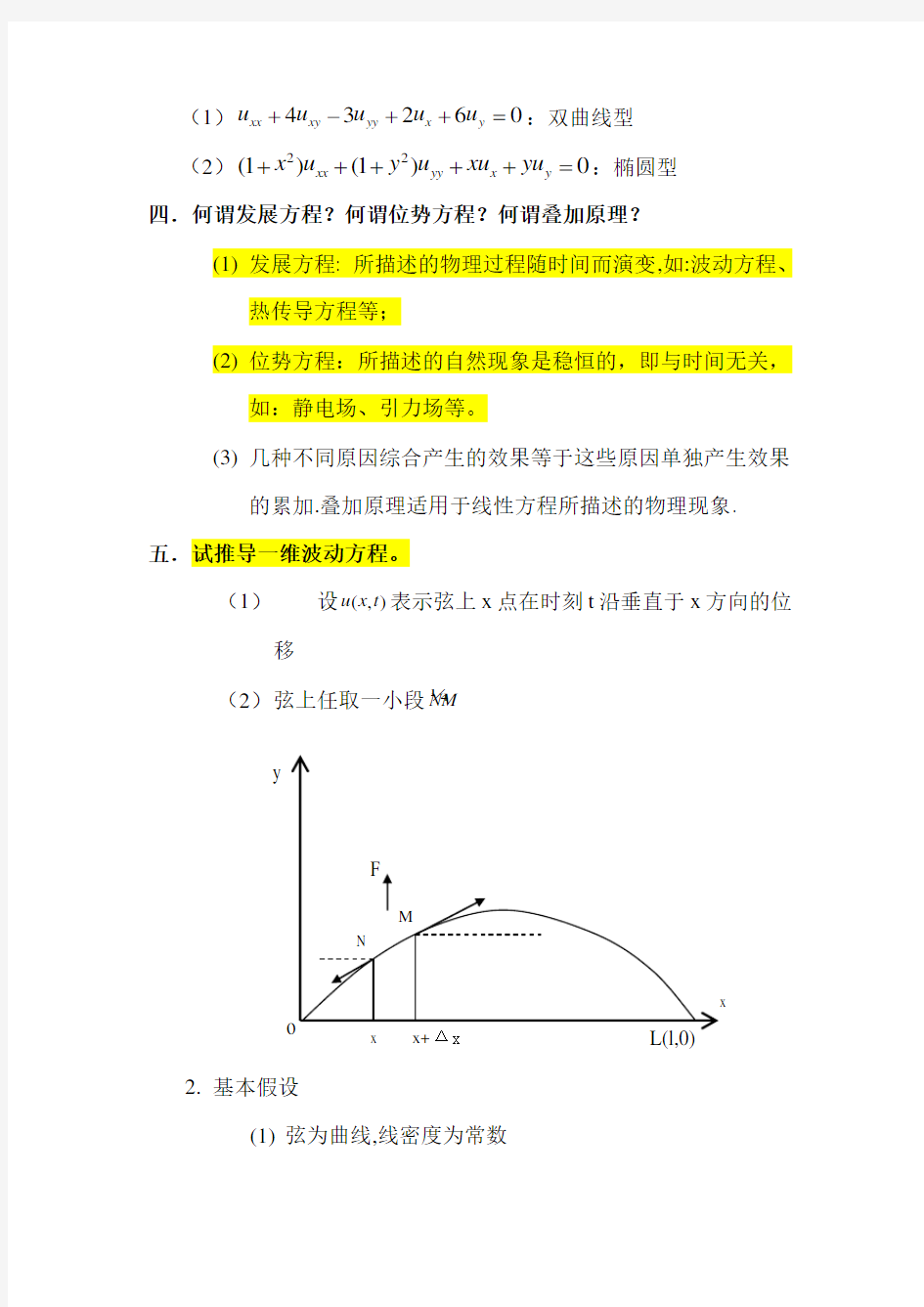
五．试推导一维波动方程。

（1） 设(,)u x t 表示弦上x 点在时刻t 沿垂直于x 方向的位

移

（2） 弦上任取一小段?

NM

2. 基本假设

(1) 弦为曲线,线密度为常数

(2) 弦在一平面内作微小振动 (3) Hooke 定律 3. 方程的建立

（1）

?NM 弧长:

x x

s +??=? s=x x x

dx x +?∴?=??

（2）

?NM 受力分析： X 轴方向: T 2con θ2 —T 1con θ1=0 （T 2= T 1=T ） Y 轴方向:

作用在M 点的张力T ，在y 轴方向的分力为2sin T θ 作用在N 点的张力T ，在y 轴方向的分力为1sin T θ- 作用在NM 点上，垂直于x 轴外力为(,)F x t x ? （3） N ewton 第二定律

21sin sin : ,sin -+?=?==

=

tt x T T F x xu tg u u θθρθθ因故

弦作微小振动时,变形很小, 2x u 与1相比可忽略不计:

[]12*

sin (,)sin (,):

(,)(,):x x x x tt xx tt u x t u x x t T u x x t u x t F x xu Tu x F x xu θθρρ≈≈+?+?-+?=??+?=?代入上式得利用中值定理得

（4） 弦强迫横振动方程:

22

: tt xx u a u f T

F

a f ρ

ρ

=+=

=

其中

（5） 弦的自由振动方程：2

tt

xx u a u =

六．简述泛定方程、定解条件、定解问题、偏微分方程古典解、定解问题的适定性的基本概念

1. 泛定方程:

描述某些物理运动或社会现象变化的普遍规律的微分方程 2. 定解条件:

微分方程满足的特定条件称为定解条件, 常见的定解条件有初始条件和边界条件。

3. 定解问题: 一个微分方程(组)和相应的定解条件合在一起就构成了一个定解问题.

4. 古典解：如果存在一个函数(,)u x t ,具有所需要的各种连续偏导数,将它们代入方程时能使方程成为恒等式,则称该函数为该方

程的(古典解)解。

5. 定解问题的适定性：存在性、唯一性、稳定性的统称 (1) 解的存在性: 所给定的定解问题至少存在一个解 (2) 解的唯一性: 所给定的定解问题至多存在一个解

(3) 解的问题性: 当给定条件以及方程中的系数有微小变动时,相应的解也只有微小的变动.

七．教材（P23）1.4习题1

解： 设t 时刻弦上x 点处位移为(,)u x t ，弦的线密度为ρ, 根据动量守恒定律可知：

0,

20,

=?-

?->??t K x c h u h t x c h

ρg

则定解问题为：

2000(0,0)0,0,

(0),20

====?=<<>?

?->?

???

==→???-

?==?tt xx t t x x l u a u x l t x c h u u h K t x c h h u

u ρ 八．教材（P23）1.4习题3

设：t 时刻弦上x 点处位移为(,)u x t ；均匀细杆的原长为l ， x=l 端自由，即应力为0，

∴

00.(,0)(,0)0,(,0),0,(,0)===?==+?==∴==

∴=l x x l u

u x kx b

x e

u x u x e b k l e u x x

l

设：已知：

则定解问题为：

200

0(0,0),

00,

0====?

?=<<>????

==???

??==????

tt xx t t x t l u a u x l t e u u x l t u

u x

九．教材（P23）1.4习题4

解：设t 时刻杆上x 点处温度为： (,)u x t

根据傅里叶定律可知：t 时刻x 处单位时间内沿x 轴方向通过横截面单位面积的热量q （x,t ）与温度的下降率成正比，即：

0(,)(,)

(,)lim

(0)

x u x t u x x t q x t K x

u

K K x

?→-+?=??=->? 则定解问题为：

200(0,0)(),20;===?

?=<<>?

-?

=

????=-=-???

t xx t x x l u a u x l t x l x u x u

u K q x

第二章： 复习思考题与作业

一． 何谓波动方程的特征值与特征函数、何谓Sturm-Liouville 问题？ P(26)

二． 简述三角函数系的正交性。

1，cosx ，sinx ，cos2x ，sin2x ，…cosnx ，sinnx ，构成了一个三角函数系,其中任意两个不同的函数的乘积在[-π,π]上的积分必为零.

三． 用变量分离法求解齐次线性偏微分方程定解问题的基本步骤。 1.思路：

(1) 放弃先求通解，再找特解的办法（放弃普通微分方程的解法）

(2) 直接探求满足定解条件的特解

(3) 求解偏微分方程→分离变量→化成求解常微分方程 (4) 启示: 机械的、电磁的振动，总可分解为具有各种频率和振幅的简谐振动的叠加，而每个简谐振动具有形式：

sin sin()A kx wt δ+，该函数具有变量分离的形式

2. 具体步骤：P33

四． 简述付氏解的物理意义。

1. 傅氏解的表达形式

1(,)cos sin sin x n n n an an

n u x t C t D t l l l πππ∞=?

?

=+ ??

?

∑

2. 傅氏解的化简:

()221(,)cos sin

x : A ;;n n n n n

n n n n n n n u x t A t l

d n a c d ctg c l π

ωθπθω-=-=+==

其中 3. 分析:

(1) 先固定时间t, 看看在任意指定时刻波的形状; 当时间取定t 0时:

'0'0(,)sin

x : A cos();

n n n n n n n u x t A l A t πωθ==-其中

表明: 波u(x,t)在任意时刻的形状是正弦曲线,只是振幅 随着时间的改变而改变.

(2) 然后固定弦上一点,看看该点的振动规律.

00(,)sin x cos()n n n n n u x t A t l

π

ωθ=-

① 弦上x 点作 ()cos n n t ωθ-表示一种谐和振动,振幅为:

0sin n n A x l

π

② 弦上各点的园频率、初相位都相同 ③

④ 驻波: 有节点的振动波

⑤ 腹点: 都是振幅达到最大值,称为腹点

4. 基波与谐波:

(1) 由于解为: 1(,)(,)n n u x t u x t ∞

==∑，因此是由无穷多个振

幅、频率、初相不相同的驻波叠加而成。 (2) 在所有驻波频率：

1,,,n na

n

l l

ππωω=

=

中最小称为基频

其他驻波的频率是基频的整数倍称为第n级谐音

(3) 固有频率：园频率n na

l

πω=

=

与初始条件无关, 只与弦的长度、密度成反比，和张力的平方根成正比

五． 求解2.1.2(P30)

六． P65: 2.7习题1

第三章 复习与思考题

一．推导一维热传导方程 1. 问题：

（1）考察一根均匀细杆内热量传播的过程 （2）热量沿x 轴一维传播,侧面绝热 （3）设(,)u x t 表示x 点在时刻t 的温度

2 方程的建立

（1）分析：考察在时间间隔t 到Δt 内,细杆上x 到x+Δx 微元段的热量流动情况 （2）热平衡方程式:

① 引起温度变化所吸收的热量ΔQ=流入的热量ΔQ ’ ② 在时间Δt 内微元段的温度升高为:

(,)(,)t u x t t u x t u t +?-=?

③ 升高上述温度所需的热量:

A

()()t t Q c A x u t c Au x t ρρ?=??=??

④ 热传导Fourier 实验定律: 流入微元段的热量: 1

(,)x Q ku x t A t ?=-?

流出微元段热量: 2(,)x Q ku x x t A t ?=-+?? 留在微元段的热量:

()[]'12

=(,)(,) =(,)(,) = (,)

x x x x xx Q Q Q ku x t A t ku x x t A t kA u x x t u x t t kAu x t x t ?=?-?-?--+??+?-???

二．简述与热传导方程相似的物理问题

1. 海底电缆电压方程

2. 导电线圈在所围柱体内的磁场方程

3. 扩散物质的浓度方程

三．何谓Poisson 方程和Laplace 方程，何谓位势方程？

1. 热传导中温度分布稳定时所满足的方程为Poisson 方程：

0u f ?+=

2. 特别地f=0时为Laplace 方程：0u ?=

3. Poisson 方程和Laplace 方程统称为位势方程 四．解2.2.1 (P38)

()()2 00(0,),=0 ,0=sin 2sin 3t xx u a u u t u t u x x x

ππ==+

五．解2.2.2 (P39) ：求解细杆导热问题，杆长为L ，两端保持为

六 P66习题(4)（?）

第4章 Fourier 变换

1. 何谓傅氏变换？简述其物理意义。

（1）若f(x) 满足傅氏积分定理条件，则称表达式

()i ()d +∞

--∞

=?

x F f x e x ωω 为f(x)Fourier 变换

（2）物理意义：

2. 简述Fourier 变换求解偏微分方程的基本步骤

（1） 根据自变量的变化范围及定解条件的情形,确定关于那个变量作变换,对方程两边施以Fourier 变换,使偏微分方程转化为关于未知函数的Fourier 变换(像函数)的常微分方程

（2）对定解条件进行相应的变换,导出常微分方程的定解条件 （3）解常微分方程定解问题,求得原定解问题解的像函数

（4）对所得像函数进行逆变换,得偏微分方程定解问题形式解 （5）必要时,验证在一定条件下,形式解就是所求问题的古典解 3. 推导无限长弦的d’Alembert 公式

（1）2

t=0, -<,0(,0)(), (); -??==∞<+∞??

tt

xx t u a u x t u x x u x x ?ψ （2）对方程两边关于x 作Fourier 变换

[][]222

2

t=0??0?(), (); =?+=???==?t t d u a u dt u F u F λ?λψλ

（3）求特征方程、特征值

()()()()22

222

12,,?''00

? ; =+-?+=?

→=±?+=??=i t i t t t u a u r i a r a u

e u e αβαβλλλλλ

（4）代入初值条件，求得常微分方程的解

()1212?(,)cos C sin ?()?(), C ; ?=+?

?==?

?

t u t e C t t C a αλββψλ?λλ （5）作关于λ的Fourier 逆变换

()()???(,)cos sin ?1122--=+????=++-??????

i at i at

i at i at u t at at

a

e e e e a i i λλλλψ

λλ?λλλλψψ??λλ （6）求得原偏微分方程的解(无限长弦的d’Alembert 公式)

()()11(,)()22+-=++-+?????x at x at

u x t x at x at d a ??ψξξ 4. 试用Fourier 变换求解波动方程的Cauchy 问题 书P79例3.2.2（同上一题）

5. 求解热传导方程的初值问题：书93页习题3.6：（6）

2

t=00, -<,0cos ?-=∞<+∞>??=??

t xx u a u x t u x 第5章 Laplace 变换

1. 简述Laplace 变换及存在定理

（1）若f(x) 在[0,+∞]上有定义，对于复数p, 则称表达式

()0

()d +∞

-=?

px F p f x e x 为f(x) Laplace 变换

（2）P81

2. 简述Laplace 变换求解偏微分方程的基本步骤

（1） 根据自变量的变化范围及定解条件的情形,确定关于那个变量作变换,对方程两边施以Laplace 变换,使偏微分方程转化为关于未知函数的Laplace 变换(像函数)的常微分方程

（2）对定解条件进行相应的变换,导出代数方程或常微分方程的定解条件

（3）解常微分方程定解问题,求得原定解问题解的像函数 （4）对所得像函数进行逆变换,得偏微分方程定解问题形式解 （5）必要时,验证在一定条件下,形式解就是所求问题的古典解

3. 用Laplace 积分变换法求解下列定解问题: 书93页习题3.6：（12）

第六章 数学物理方程的差分解法

1. 试写出导数的前差、后差和中央差商近似差分格式。

001 0,0

11==?=>>??

=+??

=??

xy x y u x y u y u

2. 写出

''''

()

()(1) (2) +-x h x h u u 的中央差分格式

3. 写出二维Laplace 方程的差分方程

4.

写出一维波动方程的差分格式

5. 设区域Ω是边长为1,中心在原点的正方形,用差分解法(取步长h=0.1)求Laplace 方程的解的第一次近似值Ui,j:(取零次近似值为

(0),0=i j U ,采用同步迭代法)

22221122

=0 1,1=±=±

???+?????

?=-=??x y u u

x y u u

6. 用差分方法求下列定解问题的近似解

2222040

2040 :02(2), 0

sin , 04====?<

?<

=-=??

?==??

x x y y x u u D y x

y u y y u u x u π