振动理论及应用期末复习题题汇总

2008年振动力学期末考试试题
第一题(20分)
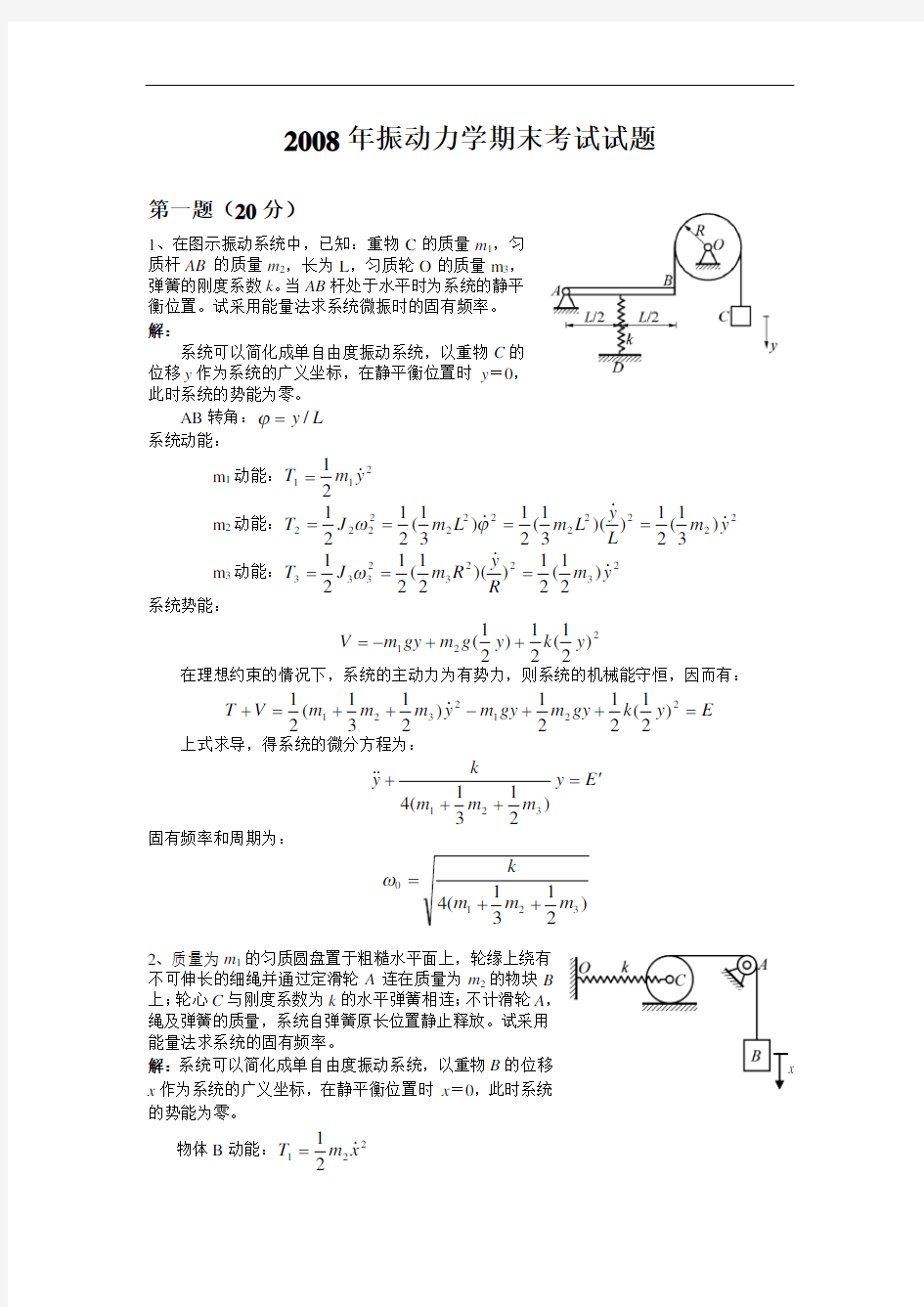
1、在图示振动系统中,已知:重物C 的质量m 1,匀质杆AB 的质量m 2,长为L ,匀质轮O 的质量m 3,弹簧的刚度系数k 。当AB 杆处于水平时为系统的静平衡位置。试采用能量法求系统微振时的固有频率。 解:
系统可以简化成单自由度振动系统,以重物C 的位移y 作为系统的广义坐标,在静平衡位置时 y =0,此时系统的势能为零。
AB 转角:L y /=? 系统动能:
m 1动能:2112
1
y m T =
m 2动能:2222222
22222)3
1(21))(31(21)31(2121y m L y L m L m J T ====?
ω m 3动能:2322
32333)2
1(21))(21(2121y
m R y R m J T ===ω 系统势能:
221)2
1
(21)21(y k y g m gy m V ++-=
在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有:
E y k gy m gy m y
m m m V T =++-++=
+2212321)2
1
(2121)2131(21 上式求导,得系统的微分方程为:
E y m m m k
y
'=+++)
2
1
31(4321
固有频率和周期为:
)
2
131(43210m m m k
++=
ω
2、质量为m 1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮A 连在质量为m 2的物块B 上;轮心C 与刚度系数为k 的水平弹簧相连;不计滑轮A ,绳及弹簧的质量,系统自弹簧原长位置静止释放。试采用能量法求系统的固有频率。
解:系统可以简化成单自由度振动系统,以重物B 的位移x 作为系统的广义坐标,在静平衡位置时 x =0,此时系统的势能为零。
物体B 动能:2212
1
x m T =
x
轮子与地面接触点为速度瞬心,则轮心速度为x v c 21=,角速度为x R
21=ω,转过的角度为x R
21
=
θ。轮子动能: )83
(21)41)(21(21)41(212121212221212212x m x R
R m x
m J v m T c =+=+=ω 系统势能:
22228)21(21)(2121x k
xR R k R k kx V c ====
θ 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,有:
E x k
x
m m V T =++=
+22218
)83(21 上式求导得系统的运动微分方程:
08322
1=++x m m k
x
固有频率为:
2
10832m m k
+=
ω
第二题(20分)
1、在图示振动系统中,重物质量为m ,外壳质量为2m ,每个弹簧的刚度系数均为k 。设外壳只能沿铅垂方向运动。采用影响系数方法:(1)以x 1和x 2为广义坐标,建立系统的微分方程;(2)求系统的固有频率。 解:
系统为二自由度系统。
当x1=1,x2=0时,有:k11=2k ,k21=-2k 当x2=1,x2=1时,有:k22=4k ,k12=-2k 因此系统刚度矩阵为:
??
?
??
?--k k k k 4222 系统质量矩阵为:
??
????m m 200 系统动力学方程为:
??
?
???=????????????--+????????????0042222002121x x k k
k k x x m m
频率方程为:
024222)(Δ2
2
=----=
ω
ωωm k k
k
m k 解出系统2个固有频率:
m k )
22(21-=ω,m
k )22(2
2+=ω
2、在图示振动系统中,物体A 、B 的质量均为m ,弹簧的刚度系数均为k ,刚杆AD 的质量忽略不计,杆水平时为系统的平衡位置。采用影响系数方法,试求:(1)以x 1和x 2为广义坐标,求系统作微振动的微分方程;(2)系统的固有频率方程。 解:
系统可以简化为二自由度振动系统,以物体A 和B 在铅垂方向的位移x 1和x 2为系统的广义坐标。
当x1=1,x2=0时,AD 转角为L 3/1=θ,两个弹簧处的弹性力分别为L k θ和L k θ2。对D 点取
力矩平衡,有:kL k 9
14
11=;另外有kL k -=21。
同理,当x2=1,x2=1时,可求得:
kL k =22,kL k -=12 因此,系统刚度矩阵为:
???
?
????--kL kL kL kL 914 系统质量矩阵为:
??
????m m 00 系统动力学方程为:
??????=?????????
?????--+????????????00914002121x x kL kL kL kL x x m m
频率方程为:
09
142
2=----ωωm kL kL
kL m kL
即:
0523922242=+-L k kmL m ωω
第三题(20分)
在图示振动系统中,已知:物体的质量m 1、m 2及弹簧的刚度系数为k 1、k 2、k 3、k 4。(1)采用影响系数方法建立系统的振动微分方程;(2)若k 1= k 3=k 4= k 0,又k 2=2 k 0,求系统固有频率;(3)取k 0 =1,m 1=8/9,m 2 =1,系统初始位移条件为x 1(0)=9和x 2(0)=0,初始速度都为零,采用模态叠加法求系统响应。 解:
(1)系统可以简化为二自由度振动系统。 当x1=1,x2=0时,有:
k11=k1+k2+k4,k21=-k2
D
kL 3
2 kL 31 1?k
11k
2x 1x x 1 x 2
当x2=1,x2=1时,有:k22=k2+k3,k12=-k2。因此,系统刚度矩阵为:
???
??
?+--++3222421k k k
k k k k 系统质量矩阵为:
??
???
?21
00m m 系统动力学方程为:
??
?
???=???????????
?+--+++???????????
?00002132224212121x x k k k k k k k x x m m
(2)当0431k k k k ===,022k k =时,运动微分方程用矩阵表示为:
??
?
???=????????????--+???????????
?003224002100002121
x x k k k k x x
m m 频率方程为:
04)3)(4(20220210=---k m k m k ωω
08)43(2
02021421=++-k k m m m m ωω
求得:
)168943(22
22121212
1021m m m m m m m m k +--+?=
ω
)168943(22
22121212
1022m m m m m m m m k +-++?=
ω
(3)当k 0=1,m 1=8/9,m 2 =1时,系统质量阵:
???
?
????=10098M 系统刚度阵:
??
????--=3224K
固有频率为:
2
321=
ω,62
2=ω 主模态矩阵为:
???
????
?-=11234
3Φ 主质量阵:
???
?
????==30023M ΦΦM T
p 主刚度阵:
???
?
????==18004
9K ΦΦK T
p 模态空间初始条件:
??
????-=??????=??????-44)0()0()0()0(21
121x x q q Φ, ??
????=??????=??????-00)0()0()0()0(21
121x x q q Φ 模态响应:
01211=+q q ω ,022
22=+q q ω
即:
t t q 11cos 4)(ω=,t t q 22cos 4)(ω-=
因此有:
???-+=??????=??????t t t t t q t q t x t x 2
1212121cos 4cos 4cos 6cos 3)()()()(ωωωωΦ
第四题(20分)
一匀质杆质量为m ,长度为L ,两端用弹簧支承,弹簧的刚度系数为k 1和k 2。杆质心C 上沿x 方向作用
有简谐外部激励t ωsin 。图示水平位置为静平衡位置。(1)以x 和θ为广义坐标,采用影响系数方法建立系统的振动微分方程;(2)取参数值为m=12,L =1,k 1 =1,k 2 =3,求出系统固有频率;(2)系统参数仍取前值,试问当外部激励的频率ω为多少时,能够使得杆件只有θ方向的角振动,而无x 方向的振动? 解:
(1)系统可以简化为二自由度振动系统,选x 、θ为广义坐标,x 为质心的纵向位移,θ 为刚杆的角位移,如图示。
当1=x 、0=θ时:
2111k k k +=,2
)
(1221L k k k -= 当0=x 、1=θ时:
2
)(1211L
k k k -=,4)(22122L k k k +=
θ
x
C t ωsin
因此,刚度矩阵为:
?
?
???
??
??
?
+--+=4)(2)(2)
(22112122
1L k k L
k k L k k k k K 质量矩阵为:
???
?????=212100mL m M 系统动力学方程:
??????=???????????
?????
+--++??????????????0sin 4)(2)
(2)
(121002*********t x L k k L k k L k k k k x mL m ωθθ
(2)当m=12,L =,k 1 =1,k 2 =3时,系统动力学方程为:
?
?
????=????????????+????????????0sin 111410012t x x ωθθ
频率方程为:
011
112420
2
=--ω
ω
即:
0316122
040=+-ωω
求得:
6
7
420±=
ω (3)令t x x ωθθsin ??
?
???=??????,代入上述动力学方程,有:
??
?
???=??????????????--0111112422θωωx 由第二行方程,解得2
1ω
θ--
=x
,代入第一行的方程,有:
2
1
k ?
?θ 1=
1
)124(12
2---=ωωx ,]1)124[(2
---=ωθ 要使得杆件只有θ方向的角振动,而无x 方向的振动,则需0=x ,因此1=ω。
第五题(20分)
如图所示等截面悬臂梁,梁长度为L ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。在梁的a 位置作用有集中载荷)(t F 。已知梁的初始
条件为:)()0,(1x f x y =,)()0,(2x f x y = 。(1)
推导梁的正交性条件;(2)写出求解梁的响应)
,(t x y 的详细过程。
(假定已知第i 阶固有频率为i ω,相应的模态函数为)(x i φ,∞=~1i )
提示:梁的动力学方程为:),(]),([222222t x f t
y S x t x y EI x =??+????ρ,其中)()(),(a x t F t x f -=δ,δ为δ函数。
解:
(1)梁的弯曲振动的动力学方程为:
0),(]),([222222=??+????t
t x y S x t x y EI x ρ ),(t x y 可写为:
)sin()()()(),(θωφφ+==t a x t q x t x y
代入梁的动力学方程,有:
φρωφS EI 2)(=''''
设与i ω、j ω对应有i φ、j φ,有: i i i S EI φρωφ2)(=''''
(1)
j j j S EI φρωφ2
)(=''''
(2)
式(1)两边乘以j φ并沿梁长对x 积分,有:
??=''''l
j i i l
i j dx S dx EI 0
20
)(φφρωφφ (3)
利用分部积分,上式左边可写为:
??''''+'''-'''=''''l l
j i l i j l i j i j dx EI EI EI dx EI 0
00)()()(φ
φφφφφφφ (4)
由于在梁的简单边界上,总有挠度或剪力中的一个与转角或弯矩中的一个同时为零,所以,
上式右边第一、第二项等于零,成为:
??''''=''''l l
j i i j dx EI dx EI 0
)(φ
φφφ 将上式代入(3)中,有:
?
?=''''l
l
j i i j i dx S dx EI 0
2
φφρωφφ
(5)
式(2)乘i φ并沿梁长对x 积分,同样可得到:
??=''''l
l
j
i j
j
i dx S dx EI 0
2
φφρωφ
φ (6)
由式(5)、(6)得:
?=-l
j i j
i dx S 0
220)(φφρωω
(7)
如果j i ≠时,j i ωω≠,则有:
?=l
j
i dx S 0
0φφρ 当j i ≠
(8)
上式即梁的主振型关于质量的正交性。再由(3)及(6)可得:
?=''''l
j
i dx EI 0
0φ
φ 当j i ≠ ?=''''l i
j
dx EI 0
0)(φφ 当j i ≠
上两式即梁的主振型关于刚度的正交性。
当j i =时,式(7)总能成立,令:
?=l
pj j
M dx S 0
2φ
ρ
pj M 、pj K 即为第j 阶主质量和第j 阶主刚度。
由式(6)知有:pj
pj j M K =
2
ω
如果主振型)(x j φ中的常数按下列归一化条件来确定:
10
2==?pj l
j
M dx S φ
ρ
(9)
则所得的主振型称为正则振型,这时相应的第j 阶主刚度pj K 为2
j ω。
式(9)与(8)可合并写为:
?=l ij j
i dx S 0
δφφρ
由式(6)知有:?=''''l ij
j j
i dx EI 0
2
δωφ
φ, ?=''''l
ij j j
j
dx EI 0
2)(δωφφ
(2)悬臂梁的运动微分方程为: ),(2244t x f t
y
S x y EI =??+??ρ (1)
其中:
)()(),(a x t F t x f -=δ
(2)
令:
∑∞
==1
)()(),(i i i t q x t x y φ
(3)
代入运动微分方程,有:
),()(1
1
t x f q S q EI i i i i i i =+''"∑∑∞
=∞
= φρφ (4)
上式两边乘)(x j φ,并沿梁长度对x 进行积分,有:
?∑?∑?
=+''"∞=∞
=L j i L j i i i L j i i dx t x f dx S q
dx EI q 0
1
1
),()(φφφρφφ (5)
利用正交性条件,可得:
)()()(2t Q t q t q j j j j =+ω
(6)
其中广义力为:
)()()()()()(0
a t F dx a x t F dx t f t Q j L
j L
j j φφδφ=-==??
(7)
初始条件可写为:
???
????
====∑∑∞
=∞
=121
1)0()()()0,()0()()()0,(i i i i i i q x x f x y q x x f x y φφ (8)
上式乘以)(x S j φρ,并沿梁长度对x 积分,由正交性条件可得:
?????==??dx
x x Sf q dx
x x Sf q j L
j
j L j
)()()0()()()0(0201φρφρ (9)
由式(6),可得:
??
-+
+
=-+
+
=L
j j j
j j
j j j L j j j
j j
j j j j d t F a t q
t q d t Q t q
t q t q 0
)(sin )()(1
sin )0(cos )0()(sin )(1
sin )0(cos )0()(τ
τωτφωωωωτ
τωτωωωω (10)
利用式(3),梁的响应为:
∑?∑∞
=∞
=??
?
?????-++==101
)(sin )()(1
sin )0(cos )0()()
()(),(i L j j j j j j j j i i i i d t F a t q t q x t q x t x y ττωτφωωωωφφ
