拉普拉斯变换及其逆变换表
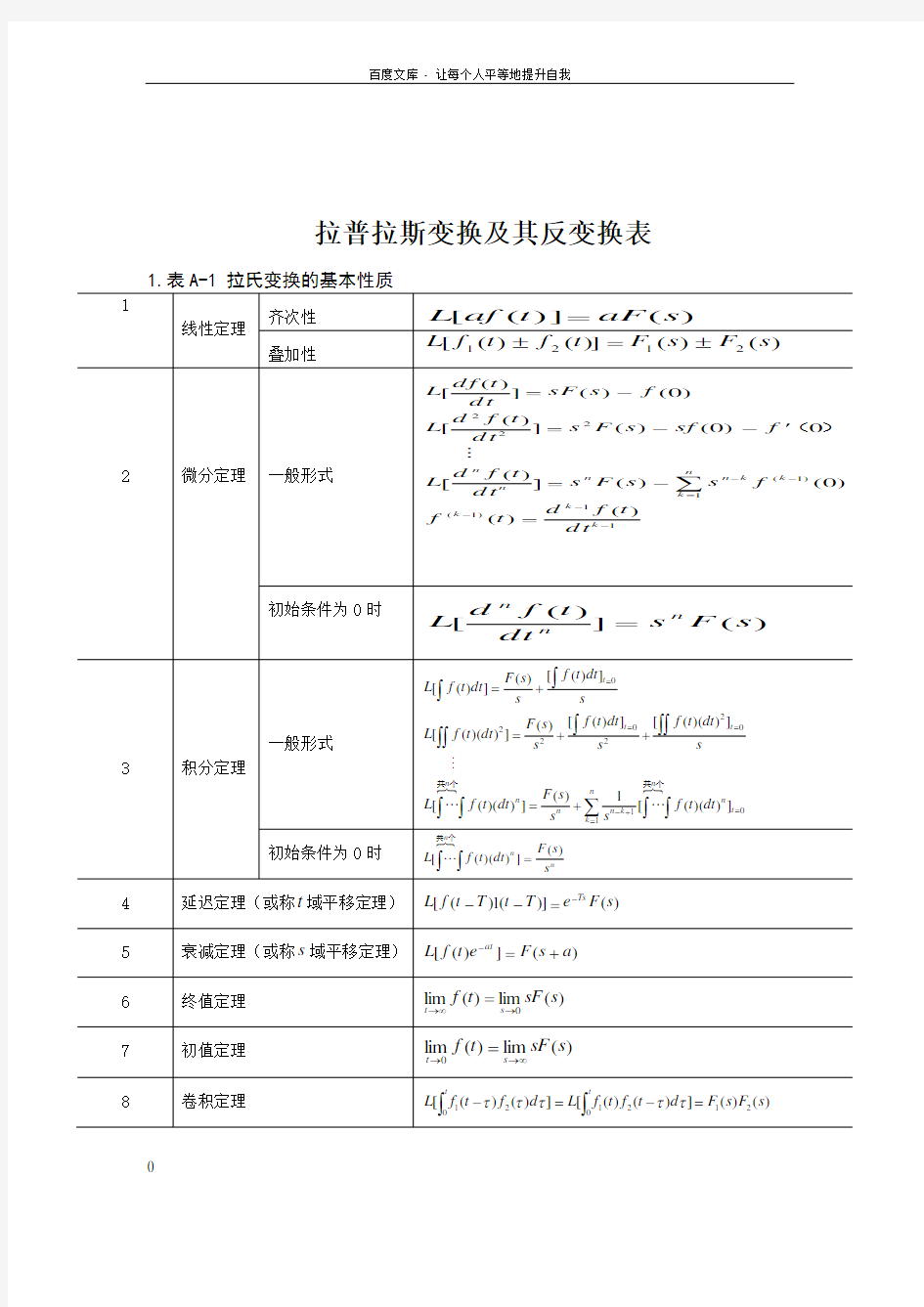

拉普拉斯变换及其反变换表
1
线性定理
齐次性
)()]([s aF t af L =
叠加性
)()()]()([2121s F s F t f t f L ±=±
2
微分定理
一般形式
=
-
=][
'- -=-=----=-∑1
1)
1()
1(1
22
2)()()
0()()
(0)0()(])([)
0()(])
([
k k k k n
k k
n n n
n
dt t f d t f f
s
s F s dt t f d
L f sf s F s dt
t f d L f s sF dt
t df L )(
初始条件为0时
)(])
([
s F s
dt t f d
L n
n
n
=
3
积分定理
一般形式
∑???????????==+-===+=+
+=+=
n
k t n n k n n n
n t t t dt t f s s s F dt t f L s
dt t f s dt t f s s F dt t f L s
dt t f s s F dt t f L 10
102
2022
]))(([1)(])()([]))(([])([)(]))(([])([)(])([个
共个
共
初始条件为0时
n n n s
s F dt t f L )
(]))(([=??个
共
4 延迟定理(或称t 域平移定理) )()](1)([s F e T t T t f L Ts -=--
5 衰减定理(或称s 域平移定理) )(])([a s F e t f L at +=-
6 终值定理 )(lim )(lim 0
s sF t f s t →∞
→=
7 初值定理 )(lim )(lim 0
s sF t f s t ∞
→→=
8
卷积定理
)()(])()([])()([210
210
21s F s F d t f t f L d f t f L t
t =-=-??τττττ
1
序号
拉氏变换F(s)
时间函数f(t) Z 变换F(z)
1 1
δ(t) 1
2 Ts
e
--11
∑∞
=-=0)()(n T nT t t δδ
1
-z z 3 s
1 )(1t
1
-z z 4 2
1s t
2
)1(-z Tz
5 3
1s 2
2t
3
2
)1(2)1(-+z z z T
6 1
1+n s
!n t n
)(!)1(lim 0aT
n n n a e z z a n -→-??- 7 a
s +1 at e - aT
e z z
-- 8 2
)(1a s +
at
te
-
2
)(aT aT e z Tze ---
9 )
(a s s a
+ at e --1
)
)(1()1(aT aT e z z z e ----- 10 )
)((b s a s a
b ++-
bt
at
e
e
---
bT
aT e z z
e z z ----- 11 22ω
ω
+s t ωsin
1
cos 2sin 2+-T z z T
z ωω
12 2
2ω+s s
t ωcos
1
cos 2)cos (2+--T z z T z z ωω 13 22)(ω
ω++a s t e at
ωsin - aT
aT aT e T ze z T
ze 22cos 2sin ---+-ωω 14 2
2)(ω+++a s a s
t e
at
ωcos -
aT
aT aT e T ze z T ze z 222cos 2cos ---+--ωω
15
a
T s ln )/1(1- T t a /
a
z z -
2
3. 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式
1
1
n 1
n n
n
1
1
m 1
m m
m
a
s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)
式中系数n
1
n 1
a ,a ,...,a ,a
-,m
1
m 1
b ,b ,b ,b - 都是实常数;n m ,是正整数。按
代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根
这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑
=-=-++-++-+-=n
1
i i
i
n
n
i
i
2
2
1
1
s
s c
s s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c i
s s i
i
-=→
或
i
s s i
)
s (A )
s (B c
='=
式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数
[]t s n 1
i i n 1i i i 11i e c s s c
L )s (F L )t (f -==--∑∑=??????-==
② 0)(=s A 有重根
设0)(=s A 有r 重根1s ,F(s)可写为
3
())
s s ()s s ()s s ()
s (B s F n
1
r r 1
---=
+
=
n
n
i
i
1
r 1
r 1
1
1
r 1
1
r r 1
r
s
s c
s s c s s c )s s (c )s s (c )s s (c -+
+-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:
)s (F )s s (lim c r
1
s s r
1
-=→
)]s (F )s s ([ds
d
lim c r
1
s s 1
r 1
-=→-
)s (F )s s (ds
d lim !j 1c r
1
)
j ()
j (s s j
r 1
-=→-
)s (F )s s (ds
d
lim )!1r (1c r
1
)
1r ()
1r (s s 1
1
--=--→
原函数)(t f 为 [])()(1s F L t f -=
??
?
???-+
+-++-+-++-+-=++---n
n
i
i
1
r 1
r 1
1
1
r 1
1
r r
1
r
1
s s c
s s c s s c )s s (c )
s s (c )s s (c L t
s n
1
r i i
t
s 1
2
2
r 1
r 1
r r
1e c e c t c t )!2r (c t )!1r (c ∑+=---+??
????+++-+-= (F-6)
