高考热点问题:立体几何中折叠问题

高考热点问题:立体几何中折叠问题
一、考情分析
立体几何中的折叠问题是历年高考命题的一大热点与难点,主要包括两个方面:一是平面图形的折叠问题,多涉及到空间中的线面关系、体积的求解以及空间角、距离的求解等问题;二是几何体的表面展开问题,主要涉及到几何体的表面积以及几何体表面上的最短距离等.
二、经验分享
(1)立体几何中的折叠问题主要包含两大问题:平面图形的折叠与几何体的表面展开.把一个平面图形按照某种要求折起,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是折叠问题.把一个几何体的表面伸展为一个平面图形从而研究几何体表面上的距离问题,这就是几何体的表面展开问题.折叠与展开问题是立体几何的两个重要问题,这两种方式的转变正是空间几何与平面几何问题转化的集中体现,展开与折叠问题就是一个由抽象到直观,由直观到抽象的过程.此类问题也是历年高考命题的一大热点. (2) 平面图形通过折叠变为立体图形,就在图形发生变化的过程中,折叠前后有些量(长度、角度等)没有发生变化,我们称其为“不变量”.求解立体几何中的折叠问题,抓住“不变量”是关键.
(3)把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.
三、题型分析
(一) 平面图形的折叠
解答折叠问题的关键在于画好折叠前后的平面图形与立体图形,抓住两个关键点:不变的线线关系、不变的数量关系.不变的线线关系,尤其是平面图形中的线线平行、线线垂直关系是证明空间平行、垂直关系的起点和重要依据;不变的数量关系是求解几何体的数字特征,如几何体的表面积、体积、空间中的角与距离等的重要依据.
1. 折叠后的形状判断
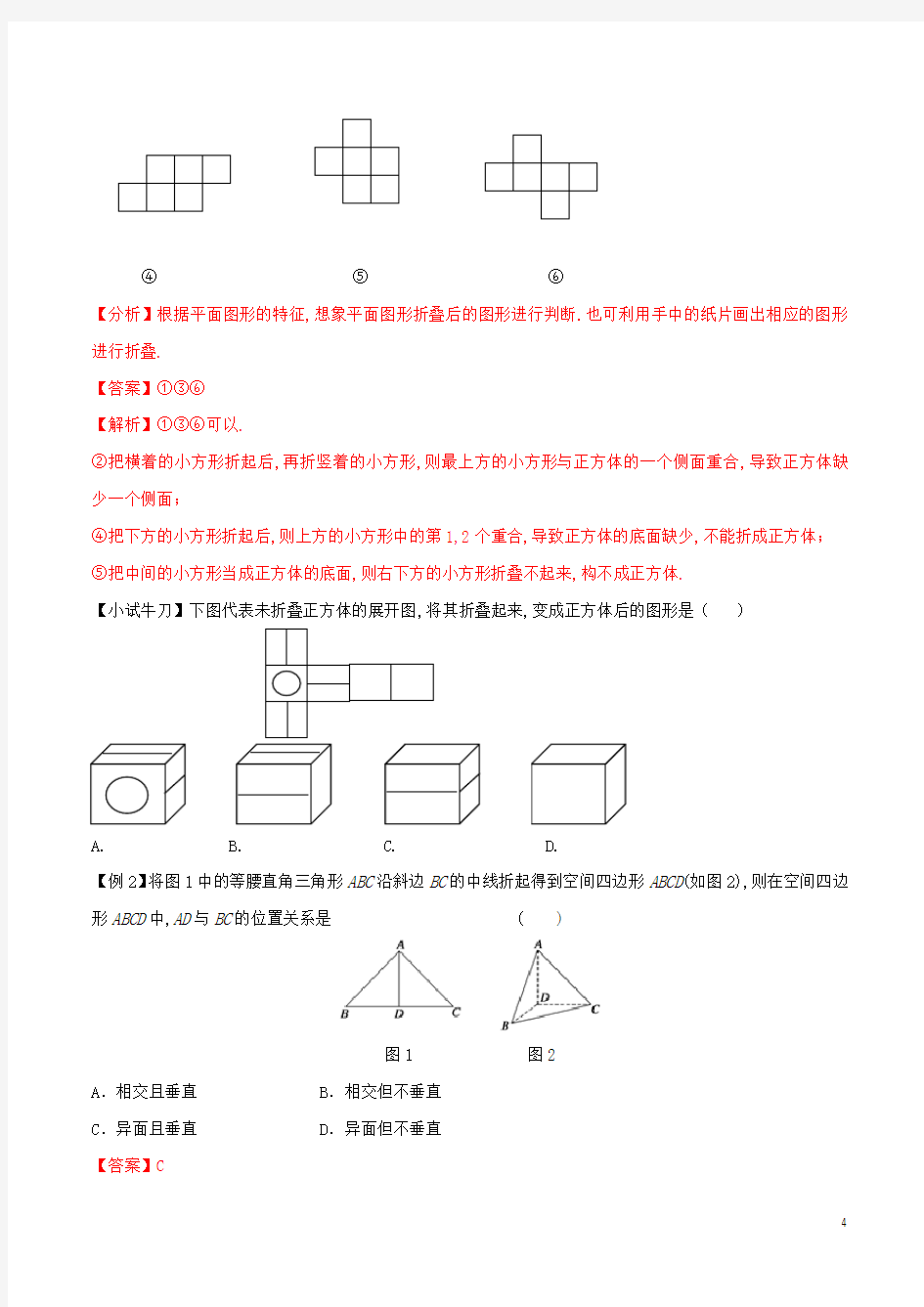
【例1】如下图,在下列六个图形中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是_____________(要求:把你认为正确图形的序号都填上)
①②③
④⑤⑥
【分析】根据平面图形的特征,想象平面图形折叠后的图形进行判断.也可利用手中的纸片画出相应的图形进行折叠.
【答案】①③⑥
【解析】①③⑥可以.
②把横着的小方形折起后,再折竖着的小方形,则最上方的小方形与正方体的一个侧面重合,导致正方体缺少一个侧面;
④把下方的小方形折起后,则上方的小方形中的第1,2个重合,导致正方体的底面缺少,不能折成正方体;
⑤把中间的小方形当成正方体的底面,则右下方的小方形折叠不起来,构不成正方体.
【小试牛刀】下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后的图形是()
A. B. C. D.
【例2】将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四边形ABCD(如图2),则在空间四边形ABCD中,AD与BC的位置关系是( )
图1 图2
A.相交且垂直B.相交但不垂直
C.异面且垂直D.异面但不垂直
【答案】C
【解析】在图1中的等腰直角三角形ABC 中,斜边上的中线AD 就是斜边上的高,则AD ⊥BC ,折叠后如图2,AD 与BC 变成异面直线,而原线段BC 变成两条线段BD 、CD ,这两条线段与AD 垂直,即AD ⊥BD ,AD ⊥CD ,故AD ⊥平面BCD ,所以AD ⊥BC .
【小试牛刀】如图,在正方形ABCD 中,点E,F 分别为边BC,AD 的中点,将
沿BF 所在直线进行翻折,将
沿DE 所在直线进行翻折,在翻折过程中( )
A. 点A 与点C 在某一位置可能重合
B. 点A 与点C 的最大距离为
C. 直线AB 与直线CD 可能垂直
D. 直线AF 与直线CE 可能垂直 3.折叠后几何体的数字特征
折叠后几何体的数字特征包括线段长度、几何体的表面积与体积、空间角与距离等,设计问题综合、全面,也是高考命题的重点.解决此类问题的关键是准确确定折叠后几何体的结构特征以及平面图形折叠前后的数量关系之间的对应.
【例3】(体积问题)如图所示,等腰ABC △的底边6
6AB =,高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF △的位置,使PE AE ⊥,记
BE x =,()V x 表示四棱锥P ACFE -的体积.
(1)求()V x 的表达式;
(2)当x 为何值时,()V x 取得最大值?
P
E
D F B C
A
【解析】(1)由折起的过程可知,PE ⊥平面ABC,96ABC S ?=,
V(x)= (036x <<)
(2)
,所以(0,6)x ∈时,'()0v x > ,V(x)单调递增;636x <<时'()0v x < ,V(x)单调递减;
因此x=6时,V(x)取得最大值126.
【小试牛刀】【河北省五个一名校联盟2019届高三下学期一诊】在平面四边形 中,
AB=BC=2,AC=AD=2,现沿对角线AC 折起,使得平面DAC
平面ABC ,则此时得到的三棱锥D-ABC
外接球的表面积为( ) A .
B .
C .
D .
【例4】(空间角问题)如左图,矩形ABCD 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且
3DE =,4BF =,将BCE ?沿BE 折起至PBE ?位置(如右图所示),连结AP 、EF 、PF ,其中
25PF =.
(Ⅰ)求证:PF ⊥平面ABED ; (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.
【解析】(Ⅰ)由翻折不变性可知, , ,
在PBF ?中, ,所以PF BF ⊥ 在图1中,易得,
在PEF ?中, ,所以PF EF ⊥
又
,BF ?平面ABED ,EF ?平面ABED ,所以PF ⊥平面ABED .
. .
A
C
D
B
E
F
图
图
A
B
C
D P
E
F
(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz -如图所示,则()6,0,0A ,
,
()0,3,0E ,()6,8,0F ,所以
, ,
,
设平面PEF 的法向量为(),,x y z =n ,则0
FP EF ??=???=??n n ,即
,解得560
x y z ?
=-???=?
令6y =-,得
,
设直线AP 与平面PEF 所成角为θ,则
81281427
. 所以直线AP 与平面PEF 所成角的正弦值为81281
427
. 方法二:过点A 作AH EF ⊥于H ,
由(Ⅰ)知PF ⊥平面ABED ,而AH ?平面ABED 所以PF AH ⊥,又,EF ?平面PEF ,PF ?平面PEF ,
所以AH ⊥平面PEF ,
所以APH ∠为直线AP 与平面PEF 所成的角. 在Rt APF ?中,
在AEF ?中,由等面积公式得
48
61
在Rt APH ?中,
所以直线AP 与平面PEF 所成角的正弦值为81281
427
. 【点评】折叠问题分析求解两原则:
解法二图
A
B
C
D P
E
F
H
x
y z A B
C D P
E
F
(1)折叠问题的探究须充分利用不变量和不变关系;
(2)折叠前后始终位于折线的同侧的几何量和位置关系保持不变.
【小试牛刀】【广东省汕头市2019届高三上学期期末】如图,已知是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足,如图,将沿DE折成四棱锥,且有平面平面BCED.
求证:平面BCED;
记的中点为M,求二面角的余弦值.
(二) 几何体的展开
几何体表面展开问题是折叠问题的逆向思维、逆过程,一般地,涉及到多面体表面距离的问题,解题时不妨将它展开成平面图形试一试.
1.展开后形状的判断
【例5】把正方体的表面沿某些棱剪开展成一个平面图形(如右下图),请根据各面上的图案判断这个正方体是()
解析:这是图③模型,在右图中,把中间的四个正方形围起来做“前后左右”四个面,有“空心圆”的正方形做“上面”,显然是正方体C的展形图,故选(C).
【小试牛刀】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、“你”、“前”分别表示正方体的______________________.
2.展开后的数字特征——表面上的最短距离问题
【例6】如图,已知圆柱体底面圆的半径为2
π
,高为2,AB CD
,分别是两底面的直径,AD BC
,是母线.若一
只小虫从A点出发,从侧面爬行到C点,求小虫爬行的最短路线的长度.
【解析】如图,将圆柱的侧面展开,
其中AB为底面周长的一半,即,2
AD=.
则小虫爬行的最短路线为线段AC.
在矩形ABCD中,.
所以小虫爬行的最短路线长度为22.
【点评】几何体表面上的最短距离需要将几何体的表面展开,将其转化为平面内的最短距离,利用平面内两点之间的距离最短求解.但要注意棱柱的侧面展开图可能有多种展开图,如长方体的表面展开图等,要把不同展开图中的最短距离进行比较,找出其中的最小值.
【小试牛刀】如图,在长方体中, ,求沿着长方体表面从A到1C的最短路线长.
四、迁移运用
1.【浙江省2019年高考模拟训练】已知四边形中,,,在将沿着翻折成三棱锥的过程中,直线与平面所成角的角均小于直线与平面所成的角,设二面角,的大小分别为,则()
A. B. C.存在 D.的大小关系无法确定
【答案】B
【解析】如图,在三棱锥中,作平面于,连,
则分别为与平面所成的角.
∵直线与平面所成角的角均小于直线与平面所成的角,
∴.
过作,垂足分别为,连,
则有,
∴分别为二面角,的平面角,
∴.
在中,,设BD的中点为O,则为边上的中线,
由可得点H在CO的左侧(如图所示),
∴.
又,
∴.
又为锐角, ∴
.
故选B .
2.【四川省德阳市2018届高三二诊】以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将ABD ?与
ACD ?折成互相垂直的两个平面,得到以下四个结论:①BD ⊥平面ACD ;②ABC ?为等边三角形;③
平面ADC ⊥平面ABC ;④点D 在平面ABC 内的射影为ABC ?的外接圆圆心.其中正确的有( ) A. ①②③ B. ②③④ C. ①②④ D. ①③④ 【答案】C
【解析】由于三角形ABC 为等腰直角三角形,故
,所以BD ⊥平面ACD ,故①正确,
排除B 选项.由于AD BD ⊥,且平面ABD ⊥平面ACD ,故AD ⊥平面BCD ,所以AD CD ⊥,由此可知
,三角形为等比三角形,故②正确,排除D 选项.由于
,且ABC ?为等边三
角形,故点D 在平面ABC 内的射影为ABC ?的外接圆圆心, ④正确,故选C .
3.已知梯形如下图所示,其中,,为线段的中点,四边形为正方形,现沿
进行折叠,使得平面
平面
,得到如图所示的几何体.已知当点满足
时,平面
平面
,
则的值为( )
A. B. C. D.
【答案】C 【解析】因为四边形
为正方形,且平面
平面,所以
两两垂直,且
,所以建立空间直角坐标系(如图所示),又因为,
,所以
,
则
,
,设平面
的法向量为
,则由
得,取,平面的法向量为,则由得,取
,
因为平面
平面
,所以,解得.故选C.
4.如图是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论错误的是( )
A .点M 到A
B 的距离为
2 B .AB 与EF 所成角是90? C .三棱锥C DNE -的体积是16
D .EF 与MC 是异面直线 【答案】D
【解析】根据正方体的平面展开图,画出它的立体图形如图所示,A 中M 到AB 的距离为
2
22
MC =
,A 正确;AB 与EF 所成角是90?,B 正确;三棱锥C DNE -的体积是
,C 正确;
//EF MC ,D 错误.
5.把正方形ABCD 沿对角线AC 折起,当以四点为顶点的三棱锥体积最大时,直线BD 和平
面ABC 所成的角的大小为( )度
A .90
B .60
C .45
D .30 【答案】C
【解析】折叠后所得的三棱锥中易知当平面ACD 垂直平面ABC 时三棱锥的体积最大.设AC 的中点为O ,则DBO ∠即为所求,而DOB ?是等腰直角三角形,所以
,故选C .
6.【辽宁省辽阳市2018学届高三第一次模拟】如图,圆形纸片的圆心为O ,半径为6cm ,该纸片上的正方形ABCD 的中心为O , E , F , G , H 为圆O 上的点, ABE , BCF , CDG , ADH 分别以AB , BC , CD , DA 为底边的等腰三角形,沿虚线剪开后,分别以AB , BC , CD , DA 为折痕折起ABE , BCF , CDG , ADH ,使得E , F , G , H 重合,得到一个四棱锥,当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的体积为__________.
【答案】
500327
π
3cm
【解析】如图:
连接OE 交AB 于点I ,设E ,F ,G ,H 重合于点P ,正方形的边长为x ()0x >,则OI=
2x , IE 62
x =-. 因为该四棱锥的侧面积是底面积的2倍,所以
,解得4x =,设该四棱锥的外接球的球心
为Q ,半径为R ,则,
,解得R 3
=
,外接球的体积
3cm
7.【山东省济南市2019届高三上学期期末】在正方形中,点,分别为,的中点,将四边形
沿
翻折,使得平面
平面
,则异面直线
与
所成角的余弦值为__________.
【答案】
【解析】
连接FC ,与DE 交于O 点,取BE 中点为N , 连接ON ,CN ,易得ON ∥BD ∴∠CON 就是异面直线与
所成角
设正方形的边长为2, OC=
,ON=
,CN=
∴cos ∠CON==
故答案为:
8.如图所示,在四边形ABCD 中,
,将四边形ABCD 沿对角线
BD 折成四面体BCD A -',使平面⊥BD A /平面BCD ,则下列结论正确的是 .
(1)BD C A ⊥'; (2)
;
(3)A C '与平面BD A '所成的角为?30; (4)四面体BCD A -'的体积为6
1
. 【答案】(2)(4)
【解析】平面⊥BD A /平面BCD CD ∴⊥平面'A BD ,/CA 与平面BD A /所成的角为'CA D ∠
,四
面
体
BCD
A -/的体积为
,
,综上(2)(4)成立.
9.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ?沿直线DE 翻折成1A DE ?,若M 为线段1AC 的中点,则在ADE ?翻折过程中,下面四个选项中正确的是 (填写所有的正确选项)
(1)||BM 是定值 (2)点M 在某个球面上运动
(3)存在某个位置,使1DE A C ⊥ (4)存在某个位置,使//MB 平面1A DE 【答案】(1)(2)(4).
【解析】取CD 中点F ,连接MF ,BF ,则1//MF DA ,//BF DE ,∴平面//MBF 平面1A DE , ∴//MB 平面1A DE ,故(4)正确;由,
为定值,FB DE =为定值,
由余弦定理可得
,∴MB 是定值,故(1)正确;
∵B 是定点,∴M 是在以B 为圆心,MB 为半径的圆上,故(2)正确;∵1AC 在平面ABCD 中的射影为
AC ,AC 与DE 不垂直,∴存在某个位置,使1DE A C ⊥错误,故(3)错误.
10.【四川省广元市高2018届第二次高考适应性统考】如图,在矩形ABCD 中, 4AB =, 2AD =, E 是CD 的中点,以AE 为折痕将DAE ?向上折起, D 变为'D ,且平面'D AE ⊥平面ABCE .
(Ⅰ)求证: 'AD EB ⊥; (Ⅱ)求二面角'A BD E --的大小. 【答案】(Ⅰ)证明见解析;(Ⅱ) 90. 【解析】(Ⅰ)证明:∵, AB 4=,
∴
,∴AE EB ⊥,
取AE 的中点M ,连结MD ',则
,
∵ 平面D AE '⊥平面ABCE ,
∴MD '⊥平面ABCE ,∴MD '⊥ BE , 从而EB ⊥平面AD E ',∴AD EB '⊥ (Ⅱ)如图建立空间直角坐标系,
则()A 4,2,0、()C 0,0,0、()B 0,2,0、()
D 3,1,2',
()E 2,0,0,从而BA =(4,0,0),
,.
设
为平面ABD '的法向量,
则可以取
设
为平面BD E '的法向量,
则可以取
因此, 12n n 0?=,有12n n ⊥,即平面ABD ' ⊥平面BD E ', 故二面角
的大小为90.
11.【福建省龙岩市2019届高三下学期教学质量检查】如图1,已知菱形的对角线交于点,点为线段的中点,
,
,将三角形
沿线段
折起到
的位置,
,如图2
所示.
(Ⅰ)证明:平面
平面;
(Ⅱ)求三棱锥的体积.
【解析】(Ⅰ)折叠前,因为四边形为菱形,所以;
所以折叠后,,, 又,平面,
所以平面
因为四边形为菱形,所以.
又点为线段的中点,所以.
所以四边形为平行四边形.
所以.
又平面,所以平面.
因为平面,所以平面平面.
(Ⅱ)图1中,由已知得,,
所以图2中,,又
所以,所以
又平面,所以
又,平面,
所以平面,
所以.
所以三棱锥的体积为.
12.【湖南省长沙市长郡中学2019届高三上学期第一次适应性考试(一模】如图,在多边形中(图1),为长方形,为正三角形,现以为折痕将折起,使点在平面
内的射影恰好在上(图2).
(Ⅰ)证明:平面;
(Ⅱ)若点在线段上,且,当点在线段上运动时,求三棱锥的体积. 【解析】(Ⅰ)过点作,垂足为.
由于点在平面内的射影恰好在上,
∴平面.
∴.
∵四边形为矩形,∴.
又,∴平面,
∴.
又由,,可得,同理.
又,∴,∴,且,
∴平面.
(Ⅱ)设点到底面的距离为,
则.
由,可知,
∴.
又,
∴.
13.【江西省上饶市重点中学2019届高三六校第一次联考】如图所示,在边长为2的菱形中,
,现将沿边折到的位置.
(1)求证:;
(2)求三棱锥体积的最大值.
【解析】(1)如图所示,
取的中点为,连接,易得,,又面
(2)由(1)知,
= ,当时,的最大值为1.
14.【云南师范大学附属中学2019届高三上学期第一次月考】如图所示甲,在四边形ABCD中,,,是边长为8的正三角形,把沿AC折起到的位置,使得平面平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
求证:平面PON;
求三棱锥的体积.
【解析】如图所示,为正三角形,O为AC的中点,
,
平面平面ACD,平面平面,
平面ACD,平面ACD,
.
,,,
,即.
,N分别为棱AC,AD的中点,
,
,
又,
平面PON;
解:由,,,可得,
点O、N分别是AC、AD的中点,
,
是边长为8的等边三角形,
,
又为PA的中点,
点M到平面ANO的距离,
.
又,
.
15.【湖北省荆门市2019届高三元月调研】如图,梯形中,,过分别作,,垂足分别,,已知,将梯形沿同侧折起,得空间几何体,如图.
1若,证明:平面;
2若,,线段上存在一点,满足与平面所成角的正弦值为,求的长.【解析】1由已知得四边形ABFE是正方形,且边长为2,在图2中,,
由已知得,,平面
又平面BDE,,
又,,平面
2在图2中,,,,即面DEFC,
在梯形DEFC中,过点D作交CF于点M,连接CE,
由题意得,,由勾股定理可得,则,,
过E作交DC于点G,可知GE,EA,EF两两垂直,
以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则,
.
设平面ACD的一个法向量为,
由得,取得,
