中考数学综合题专题复习【二次函数】专题解析及答案解析

一、二次函数真题与模拟题分类汇编(难题易错题)
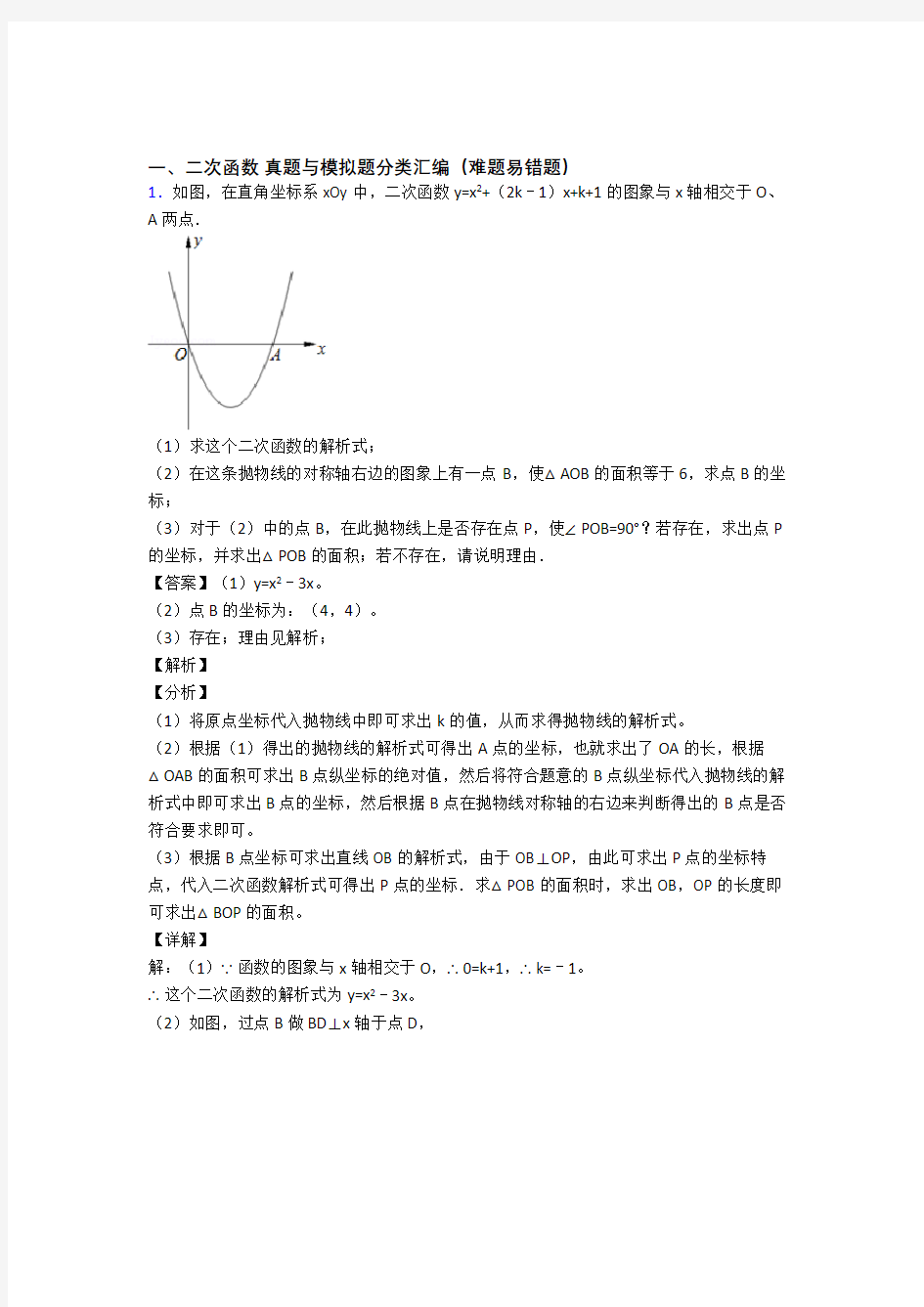
1.如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P 的坐标,并求出△POB的面积;若不存在,请说明理由.
【答案】(1)y=x2﹣3x。
(2)点B的坐标为:(4,4)。
(3)存在;理由见解析;
【解析】
【分析】
(1)将原点坐标代入抛物线中即可求出k的值,从而求得抛物线的解析式。
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可。
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,求出OB,OP的长度即可求出△BOP的面积。
【详解】
解:(1)∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1。
∴这个二次函数的解析式为y=x2﹣3x。
(2)如图,过点B做BD⊥x轴于点D,
令x 2﹣3x=0,解得:x=0或3。∴AO=3。
∵△AOB 的面积等于6,∴
1
2
AO?BD=6。∴BD=4。 ∵点B 在函数y=x 2﹣3x 的图象上,
∴4=x 2﹣3x ,解得:x=4或x=﹣1(舍去)。
又∵顶点坐标为:( 1.5,﹣2.25),且2.25<4, ∴x 轴下方不存在B 点。
∴点B 的坐标为:(4,4)。 (3)存在。
∵点B 的坐标为:(4,4),∴∠BOD=45°,22BO 442=+=。
若∠POB=90°,则∠POD=45°。 设P 点坐标为(x ,x 2﹣3x )。 ∴2
x x 3x =-。
若2x x 3x =-,解得x="4" 或x=0(舍去)。此时不存在点P (与点B 重合)。 若(
)
2
x x 3x =--,解得x="2" 或x=0(舍去)。 当x=2时,x 2﹣3x=﹣2。 ∴点P 的坐标为(2,﹣2)。 ∴22OP 222=
+=
∵∠POB=90°,∴△POB 的面积为:
12PO?BO=1
2
×2×2=8。
2.如图,抛物线y =12
x 2
+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).
(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;
(3)点M 是抛物线对称轴上的一个动点,当MC +MA 的值最小时,求点M 的坐标.
【答案】(1)抛物线的解析式为y =
213x -22x ﹣2,顶点D 的坐标为 (3
2,﹣258
);(2)△ABC 是直角三角形,证明见解析;(3)点M 的坐标为(32,﹣5
4
). 【解析】 【分析】
(1)因为点A 在抛物线上,所以将点A 代入函数解析式即可求得答案;
(2)由函数解析式可以求得其与x 轴、y 轴的交点坐标,即可求得AB 、BC 、AC 的长,由勾股定理的逆定理可得三角形的形状;
(3)根据抛物线的性质可得点A 与点B 关于对称轴x 3
2
=
对称,求出点B ,C 的坐标,根据轴对称性,可得MA =MB ,两点之间线段最短可知,MC +MB 的值最小.则BC 与直线
x 3
2=
交点即为M 点,利用得到系数法求出直线BC 的解析式,即可得到点M 的坐标. 【详解】
(1)∵点A (﹣1,0)在抛物线y 212x =+bx ﹣2上,∴2112
?-+()b ×(﹣1)﹣2=0,解得:b 32=-,∴抛物线的解析式为y 213
22
x =-x ﹣2. y 21322x =
-x ﹣212=(x 2﹣3x ﹣4 )21325228x =--(),∴顶点D 的坐标为 (325
2
8
,
-). (2)当x =0时y =﹣2,∴C (0,﹣2),OC =2. 当y =0时,213
22
x -x ﹣2=0,∴x 1=﹣1,x 2=4,∴B (4,0),∴OA =1,OB =4,AB =5.
∵AB 2=25,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2.∴△ABC 是直角三角形.
(3)∵顶点D 的坐标为 (3
2528,
-),∴抛物线的对称轴为x 32
=. ∵抛物线y 12=
x 2+bx ﹣2与x 轴交于A ,B 两点,∴点A 与点B 关于对称轴x 3
2
=对称. ∵A (﹣1,0),∴点B 的坐标为(4,0),当x =0时,y 213
22
x =
-x ﹣2=﹣2,则点C
的坐标为(0,﹣2),则BC 与直线x
3
2
=
交点即为M 点,如图,根据轴对称性,可得:MA =MB ,两点之间线段最短可知,MC
+MB 的值最小.
设直线BC 的解析式为y =kx +b ,把C (0,﹣2),B (4,0)代入,可得:2
40b k b =-??+=?
,
解得:122k b ?
=?
??=-?
,∴y 12=x ﹣2.
当x 32=
时,y 1352224=?-=-,∴点M 的坐标为(35
24-,
). 【点睛】
本题考查了待定系数法求二次函数解析式、一次函数的解析式、直角三角形的性质及判定、轴对称性质,解决本题的关键是利用待定系数法求函数的解析式.
3.(2017南宁,第26题,10分)如图,已知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中C (0,3),∠BAC 的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .
(1)直接写出a 的值、点A 的坐标及抛物线的对称轴;
(2)点P 为抛物线的对称轴上一动点,若△PAD 为等腰三角形,求出点P 的坐标; (3)证明:当直线l 绕点D 旋转时,
11AM AN
+均为定值,并求出该定值.
【答案】(1)a =13
-,A 30),抛物线的对称轴为x 32)点P 的坐标为3034);(33
【解析】
试题分析:(1)由点C 的坐标为(0,3),可知﹣9a =3,故此可求得a 的值,然后令y =0得到关于x 的方程,解关于x 的方程可得到点A 和点B 的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;
(2)利用特殊锐角三角函数值可求得∠CAO =60°,依据AE 为∠BAC 的角平分线可求得∠DAO =30°,然后利用特殊锐角三角函数值可求得OD =1,则可得到点D 的坐标.设点P 的
,a ).依据两点的距离公式可求得AD 、AP 、DP 的长,然后分为AD =PA 、AD =DP 、AP =DP 三种情况列方程求解即可;
(3)设直线MN 的解析式为y =kx +1,接下来求得点M 和点N 的横坐标,于是可得到AN 的长,然后利用特殊锐角三角函数值可求得AM 的长,最后将AM 和AN 的长代入化简即可.
试题解析:(1)∵C (0,3),∴﹣9a =3,解得:a =13
-.
令y =0得:290ax a --=,∵a ≠0,∴290x --=,解得:x =
x =∴点A 0),B (0),∴抛物线的对称轴为x
(2)∵OA OC =3,∴tan ∠CAO ∴∠CAO =60°.
∵AE 为∠BAC 的平分线,∴∠DAO =30°,∴DO =1,∴点D 的坐标为(0,1).
设点P a ).
依据两点间的距离公式可知:AD 2=4,AP 2=12+a 2,DP 2=3+(a ﹣1)2. 当AD =PA 时,4=12+a 2,方程无解.
当AD =DP 时,4=3+(a ﹣1)2,解得a =0或a =2(舍去),∴点P 0).
当AP =DP 时,12+a 2=3+(a ﹣1)2,解得a =﹣4,∴点P ,﹣4).
综上所述,点P 04).
(3)设直线AC 的解析式为y =mx +3,将点A 的坐标代入得:30+=,解得:
m ∴直线AC 的解析式为3y =+. 设直线MN 的解析式为y =kx +1.
把y =0代入y =kx +1得:kx +1=0,解得:x =1k -,∴点N 的坐标为(1
k
-,0),
∴AN =1
k
-
.
将3y =+与y =kx +1联立解得:x
,∴点M .
过点M 作MG ⊥x 轴,垂足为G .则AG
∵∠MAG =60°,∠AGM =90°,∴AM =2AG =233k +-=2323
k k --,
∴
11AM AN +=323231k k k -+-- =33232k k --=3(31)2(31)
k k -- =3
. 点睛:本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,分类讨论是解答问题(2)的关键,求得点M 的坐标和点N 的坐标是解答问题(3)的关键.
4.如图,已知直线y =﹣2x +4分别交x 轴、y 轴于点A 、B .抛物线过A 、B 两点,点P 是线段AB 上一动点,过点P 作PC ⊥x 轴于点C ,交抛物线于点D . (1)如图1,设抛物线顶点为M ,且M 的坐标是(12,9
2
),对称轴交AB 于点N . ①求抛物线的解析式;
②是否存在点P ,使四边形MNPD 为菱形?并说明理由;
(2)是否存在这样的点D ,使得四边形BOAD 的面积最大?若存在,求出此时点D 的坐标;若不存在,请说明理由.
【答案】(1)①y =﹣2x 2+2x +4;;②不存在点P ,使四边形MNPD 为菱形;;(2)存在,点D 的坐标是(1,4). 【解析】 【分析】
(1)①由一次函数图象上点的坐标特征求得点B 的坐标,设抛物线解析式为y =
a 2
1922x ??-+ ??
?,把点B 的坐标代入求得a 的值即可;
②不存在点P,使四边形MNPD为菱形.设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),根据题意知PD∥MN,所以当PD=MN时,四边形MNPD为平行四边形,
根据该等量关系列出方程﹣2m2+4m=3
2
,通过解方程求得m的值,易得点N、P的坐
标,然后推知PN=MN是否成立即可;
(2)设点D的坐标是(n,﹣2n2+2n+4),P(n,﹣2n+4).根据S四边形BOAD=S△BOA+S△ABD =4+S△ABD,则当S△ABD取最大值时,S四边形BOAD最大.根据三角形的面积公式得到函数
S△ABD=﹣2(n﹣1)2+2.由二次函数的性质求得最值.
【详解】
解:①如图1,
∵顶点M的坐标是
19
,
22
?? ???
,
∴设抛物线解析式为y=
2
19
22
a x
??
-+
?
??
(a≠0).
∵直线y=﹣2x+4交y轴于点B,∴点B的坐标是(0,4).
又∵点B在该抛物线上,
∴
2
19
22
a
??
-+
?
??
=4,
解得a=﹣2.
故该抛物线的解析式为:y=
2
19
2
22
x
??
--+
?
??
=﹣2x2+2x+4;
②不存在.理由如下:
∵抛物线y=
2
19
2
22
x
??
--+
?
??
的对称轴是直线x=
1
2
,且该直线与直线AB交于点N,
∴点N的坐标是
1
,3
2
?? ???
.
∴93
3
22
MN=-=.
设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),∴PD=(﹣2m2+2m+4)﹣(﹣2m+4)=﹣2m2+4m.
∵PD∥MN.
当PD=MN时,四边形MNPD是平行四边形,即﹣2m2+4m=3
2
.
解得 m1=1
2
(舍去),m2=
3
2
.
此时P(3
2
,1).
∵PN=5,
∴PN≠MN,
∴平行四边形MNPD不是菱形.
∴不存在点P,使四边形MNPD为菱形;(2)存在,理由如下:
设点D的坐标是(n,﹣2n2+2n+4),∵点P在线段AB上且直线PD⊥x轴,∴P(n,﹣2n+4).
由图可知S四边形BOAD=S△BOA+S△ABD.其中S△BOA=1
2
OB?OA=
1
2
×4×2=4.
则当S△ABD取最大值时,S四边形BOAD最大.
S△ABD=1
2
(y D﹣y P)(x A﹣x B)
=y D﹣y P
=﹣2n2+2n+4﹣(﹣2n+4)
=﹣2n2+4n
=﹣2(n﹣1)2+2.
当n=1时,S△ABD取得最大值2,S四边形BOAD有最大值.此时点D的坐标是(1,4).
【点睛】
主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
5.综合与探究
如图,抛物线2
6y ax bx =++经过点A(-2,0),B(4,0)两点,与y 轴交于点C ,点D 是抛物
线上一个动点,设点D 的横坐标为(14)m m <<.连接AC ,BC ,DB ,DC . (1)求抛物线的函数表达式; (2)△BCD 的面积等于△AOC 的面积的
3
4
时,求m 的值; (3)在(2)的条件下,若点M 是x 轴上的一个动点,点N 是抛物线上一动点,试判断是否存在这样的点M,使得以点B ,D ,M ,N 为顶点的四边形是平行四边形,若存在,请直接写出点M 的坐标;若不存在,请说明理由.
【答案】(1)233
642
y x x =-++;(2)3;(3)1234(8,0),(0,0),(14,0),(14,0)M M M M -. 【解析】
【分析】
(1)利用待定系数法进行求解即可;
(2)作直线DE ⊥x 轴于点E ,交BC 于点G ,作CF ⊥DE ,垂足为F ,先求出S △OAC =6,再根据
S △BCD =
34S △AOC ,得到S △BCD =92
,然后求出BC 的解析式为3
62y x =-+,则可得点G 的坐
标为3(,6)2m m -+,由此可得2
334
DG m m =-+,再根据
S △BCD =S △CDG +S △BDG =1
2
DG BO ??,可得关于m 的方程,解方程即可求得答案;
(3)存在,如下图所示,以BD 为边或者以BD 为对角线进行平行四边形的构图,以BD 为边时,有3种情况,由点D 的坐标可得点N 点纵坐标为±154,然后分点N 的纵坐标为154
和点N 的纵坐标为15
4
-
两种情况分别求解;以BD 为对角线时,有1种情况,此时N 1点与N 2点重合,根据平行四边形的对边平行且相等可求得BM 1=N 1D=4,继而求得OM 1= 8,由此即可求得答案. 【详解】
(1)抛物线2y ax bx c =++经过点A(-2,0),B(4,0),
∴426016460a b a b -+=??++=?
, 解得3432a b ?=-????=??
,
∴抛物线的函数表达式为233
642
y x x =-
++; (2)作直线DE ⊥x 轴于点E ,交BC 于点G ,作CF ⊥DE ,垂足为F , ∵点A 的坐标为(-2,0),∴OA=2,
由0x =,得6y =,∴点C 的坐标为(0,6),∴OC=6, ∴S △OAC =11
26622
OA OC ??=??=, ∵S △BCD =
3
4S △AOC , ∴S △BCD =39
642
?=,
设直线BC 的函数表达式为y kx n =+,
由B ,C 两点的坐标得406k n n +=??=?,解得326
k n ?
=-?
??=?,
∴直线BC 的函数表达式为3
62
y x =-+, ∴点G 的坐标为3
(,6)2
m m -+, ∴223333
6(6)34224
DG m m m m m =-
++--+=-+, ∵点B 的坐标为(4,0),∴OB=4,
∵S △BCD =S △CDG +S △BDG =1111
()2222
DG CF DG BE DG CF BE DG BO ??+??=?+=??, ∴S △BCD =221
33346242
m m m m -+?=-+(), ∴239
622
m m -
+=, 解得11m =(舍),23m =, ∴m 的值为3;
(3)存在,如下图所示,以BD 为边或者以BD 为对角线进行平行四边形的构图, 以BD 为边时,有3种情况, ∵D 点坐标为15(3,
)4
,∴点N 点纵坐标为±15
4,
当点N 的纵坐标为15
4
时,如点N 2, 此时23315
6424x x -
++=,解得:121,3x x =-=(舍), ∴215
(1,
)4
N -,∴2(0,0)M ; 当点N 的纵坐标为15
4
-时,如点N 3,N 4, 此时23315
6424
x x -
++=-,解得:12114,114x x ==∴315(114,)4N +-
,415
(114,)4
N -, ∴3(14,0)M ,4(14,0)M -;
以BD 为对角线时,有1种情况,此时N 1点与N 2点重合,
∵115(1,
)4
N -,D(3,154),
∴N 1D=4, ∴BM 1=N 1D=4, ∴OM 1=OB+BM 1=8, ∴M 1(8,0),
综上,点M 的坐标为:1234(80)(00)(140)(140)M M M M -,,,,,,,.
【点睛】
本题考查的是二次函数的综合题,涉及了待定系数法、三角形的面积、解一元二次方程、平行四边形的性质等知识,运用了数形结合思想、分类讨论思想等数学思想,熟练掌握和灵活运用相关知识是解题的关键.
6.如图1,抛物线2:C y ax bx =+经过点(4,0)A -、(1,3)B -两点,G 是其顶点,将抛物线C 绕点O 旋转180,得到新的抛物线'C .
(1)求抛物线C 的函数解析式及顶点G 的坐标; (2)如图2,直线12
:5
l y kx =-
经过点A ,D 是抛物线C 上的一点,设D 点的横坐标为
m (2m <-),连接DO 并延长,交抛物线'C 于点E ,交直线l 于点M ,
2DE EM =,求m 的值;
(3)如图3,在(2)的条件下,连接AG 、AB ,在直线DE 下方的抛物线C 上是否存在点P ,使得DEP GAB ∠=∠?若存在,求出点P 的横坐标;若不存在,请说明理由.
【答案】(1)2
4y x x =--,顶点为:(2,4)G -;(2)m 的值为﹣3;(3)存在,点
P 的横坐标为:74+-
7
4
. 【解析】 【分析】
(1)运用待定系数法将(4,0)A -、(1,3)B -代入2y ax bx =+中,即可求得a 和b 的值和抛物线C 解析式,再利用配方法将抛物线C 解析式化为顶点式即可求得顶点G 的坐标; (2)根据抛物线C 绕点O 旋转180,可求得新抛物线'C 的解析式,再将(4,0)A -代入
12
5
y kx =-
中,即可求得直线l 解析式,根据对称性可得点E 坐标,过点D 作//DH y 轴交直线l 于H ,过E 作//EK y 轴交直线l 于K ,由2DE EM =,即可得
1
3
ME MD =,再证明MEK ?∽MDH ?,即可得3DH EK =,建立方程求解即可; (3)连接BG ,易证ABG ?是Rt ?,90ABG ∠=,可得
1
tan tan 3DEP GAB ∠=∠=,在x 轴下方过点O 作OH OE ⊥,在OH 上截取
1
3
OH OE ==E 作ET y ⊥轴于T ,连接EH 交抛物线C 于点P ,点P 即为
所求的点;通过建立方程组求解即可. 【详解】
(1)将(4,0)A -、(1,3)B -代入2
y ax bx =+中,得1640
3a b a b -=??-=?
解得1
4a b =-??=-?
∴抛物线C 解析式为:24y x x =--,
配方,得:2
2
4(2)4y x x x =--=-++,∴顶点为:(2,4)G -;
(2)∵抛物线C 绕点O 旋转180,得到新的抛物线'C . ∴新抛物线'C 的顶点为:'(2,4)G -,二次项系数为:'1a = ∴新抛物线'C 的解析式为:22(2)44y x x x =--=- 将(4,0)A -代入125y kx =-
中,得12045k =--,解得3
5
k =-,
∴直线l 解析式为31255
y x =--, ∵2(,4)D m m m --,
∴直线DO 的解析式为(4)y m x =-+,
由抛物线C 与抛物线'C 关于原点对称,可得点D 、V 关于原点对称, ∴2(,4)E m m m -+
如图2,过点D 作//DH y 轴交直线l 于H ,过E 作//EK y 轴交直线l 于K , 则3
12(,)55H m m --
,312(,)55
K m m --, ∴2
23121712
4()5555DH m m m m m =-----=--+,
223121712
4()5555
EK m m m m m =+--=++,
∵2DE EM = ∴
1
3
ME MD =, ∵//DH y 轴,//EK y 轴
∴//DH EK ∴
MEK ?∽MDH ? ∴
1
3
EK ME DH MD ==,即3DH EK = ∴2
2171217123()5555
m m m m --+=++ 解得:13m =-,22
5
m =-,
∵2m <-
∴m 的值为:﹣3; (3)由(2)知:3m =-,
∴(3,3)D -,(3,3)E -,
OE =
如图3,连接BG ,在ABG ?中,∵2
2
2
(14)(30)18AB =-++-=,22BG =,
220AG =
∴222AB BG AG +=
∴ABG ?是直角三角形,90ABG ∠=,
∴1
tan 3
BG GAB AB ∠=
==, ∵DEP GAB ∠=∠
∴1tan tan 3
DEP GAB ∠=∠=
, 在x
轴下方过点O 作OH OE ⊥,在OH 上截取1
23
OH OE =
=, 过点E 作ET y ⊥轴于T ,连接EH 交抛物线C 于点P ,点P 即为所求的点; ∵(3,3)E -, ∴45EOT ∠= ∵90EOH ∠= ∴45HOT ∠=
∴(1,1)H --,设直线EH 解析式为y px q =+,
则331p q p q +=-??-+=-?,解得12
32p q ?=-????=-??
∴直线EH 解析式为13
22
y x =-
-, 解方程组213224y x y x x ?=--???=--?,得11773735x y ?--=???
-?=??,2
2773
735x y ?-+=???+?=-??
, ∴点P 的横坐标为:773+-
或737
-.
【点睛】
本题考查了二次函数图象和性质,待定系数法求函数解析式,旋转变换,相似三角形判定和性质,直线与抛物线交点,解直角三角形等知识点;属于中考压轴题型,综合性强,难度较大.
7.如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P
﹣1,2);②P (﹣32
,154) 【解析】
试题分析:(1)将B 、C 的坐标代入已知的抛物线的解析式,由对称轴为1x =-即可得到抛物线的解析式;
(2)①首先求得抛物线与x 轴的交点坐标,然后根据已知条件得到PD=OA ,从而得到方程求得x 的值即可求得点P 的坐标;
②ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线2
y ax bx c =++与x 轴交于点A 和点B (1,0),与y 轴交于
点C (0,3),其对称轴l 为1x =-,∴0
{3
1
2a b c c b
a
++==-=-,解得:1
{23a b c =-=-=,∴二次函数的
解析式为223y x x =--+=2
(1)4x -++,∴顶点坐标为(﹣1,4);
(2)令2
230y x x =--+=,解得3x =-或1x =,∴点A (﹣3,0),B (1,0),作
PD ⊥x 轴于点D ,∵点P 在223y x x =--+上,∴设点P (x ,223x x --+), ①∵PA ⊥NA ,且PA=NA ,∴△PAD ≌△AND ,∴OA=PD ,即2232y x x =--+=,解得
1(舍去)或
x=1,∴点P
(1,2);
②设P(x ,y),则223y x x =--+,∵ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形
=
12OB?OC +12AD?PD+12
(PD+OC)?OD=111
31+(3)(3)()222x y y x ???+++-=
333222x y -+ =2
333(23)222x x x -+--+=239622x x --+=23375()228
x -++, ∴当x=32-时,ABCP S 四边形最大值=758,当x=32
-时,223y x x =--+=15
4,此时P
(32
-,15
4).
考点:1.二次函数综合题;2.二次函数的最值;3.最值问题;4.压轴题.
8.如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ 上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为
1
2
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
【答案】(1)抛物线y=-x2+2x+3;(2)①点D(315
24
,);②△PQD面积的最大值为8
【解析】
分析:(1)根据点A、B的坐标,利用待定系数法即可求出抛物线的表达式;
(2)(I)由点P的横坐标可得出点P、Q的坐标,利用待定系数法可求出直线PQ的表达式,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐
标为(x,-x+5
4
),进而即可得出DE的长度,利用三角形的面积公式可得出S△DPQ=-
2x2+6x+7
2
,再利用二次函数的性质即可解决最值问题;
(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,进而可得出点P、Q的坐
标,利用待定系数法可求出直线PQ 的表达式,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-2(t+1)x+t 2+4t+3),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+4(t+2)x-2t 2-8t ,再利用二次函数的性质即可解决最值问题. 详解:(1)将A (-1,0)、B (3,0)代入y=ax 2+bx+3,得:
309330a b a b -+??++?==,解得:1
2a b -??
?
==, ∴抛物线的表达式为y=-x 2+2x+3. (2)(I )当点P 的横坐标为-12
时,点Q 的横坐标为7
2,
∴此时点
P 的坐标为(-
12,74
),点Q 的坐标为(72,-9
4).
设直线PQ 的表达式为y=mx+n ,
将P (-
12,74
)、Q (72,-9
4)代入y=mx+n ,得:
1
724
792
4m n m n ?-+????+-??==,解得:154m n -?????==,
∴直线PQ 的表达式为y=-x+
5
4
. 如图②,过点D 作DE ∥y 轴交直线PQ 于点E ,
设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-x+5
4
), ∴DE=-x 2+2x+3-(-x+5
4)=-x 2+3x+74
, ∴S △DPQ =
12
DE?(x Q -x P )=-2x 2+6x+72=-2(x-3
2)2+8.
∵-2<0,
∴当x=32时,△DPQ 的面积取最大值,最大值为8,此时点D 的坐标为(32
,15
4).
(II )假设存在,设点P 的横坐标为t ,则点Q 的横坐标为4+t ,
∴点P 的坐标为(t ,-t 2+2t+3),点Q 的坐标为(4+t ,-(4+t )2+2(4+t )+3), 利用待定系数法易知,直线PQ 的表达式为y=-2(t+1)x+t 2+4t+3.
设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-2(t+1)x+t 2+4t+3), ∴DE=-x 2+2x+3-[-2(t+1)x+t 2+4t+3]=-x 2+2(t+2)x-t 2-4t ,
∴S △DPQ =
1
2
DE?(x Q -x P )=-2x 2+4(t+2)x-2t 2-8t=-2[x-(t+2)]2+8. ∵-2<0,
∴当x=t+2时,△DPQ 的面积取最大值,最大值为8.
∴假设成立,即直尺在平移过程中,△DPQ 面积有最大值,面积的最大值为8. 点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、三角形的面积以及二次函数的最值,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)(I )利用三角形的面积公式找出S △DPQ =-2x 2+6x+
7
2
;(II )利用三角形的面积公式找出S △DPQ =-2x 2+4(t+2)x-2t 2-8t .
9.如图,矩形OABC 的两边在坐标轴上,点A 的坐标为(10,0),抛物线y=ax 2+bx+4过点B ,C 两点,且与x 轴的一个交点为D (﹣2,0),点P 是线段CB 上的动点,设CP =t (0<t <10).
(1)请直接写出B 、C 两点的坐标及抛物线的解析式;
(2)过点P 作PE ⊥BC ,交抛物线于点E ,连接BE ,当t 为何值时,∠PBE =∠OCD ? (3)点Q 是x 轴上的动点,过点P 作PM ∥BQ ,交CQ 于点M ,作PN ∥CQ ,交BQ 于点N ,当四边形PMQN 为正方形时,请求出t 的值.
【答案】(1)B (10,4),C (0,4),215463y x x =-++;(2)3;(3)103或 203
. 【解析】
试题分析:(1)由抛物线的解析式可求得C 点坐标,由矩形的性质可求得B 点坐标,由B 、D 的坐标,利用待定系数法可求得抛物线解析式;
(2)可设P (t ,4),则可表示出E 点坐标,从而可表示出PB 、PE 的长,由条件可证得△PBE ∽△OCD ,利用相似三角形的性质可得到关于t 的方程,可求得t 的值;
(3)当四边形PMQN 为正方形时,则可证得△COQ ∽△QAB ,利用相似三角形的性质可求得CQ 的长,在Rt △BCQ 中可求得BQ 、CQ ,则可用t 分别表示出PM 和PN ,可得到关于t 的方程,可求得t 的值. 试题解析:
