图的基本知识

完成题库中的P1135、P1138、P1465、P1466、P1471、P1545~

图的基本知识

一、什么是图

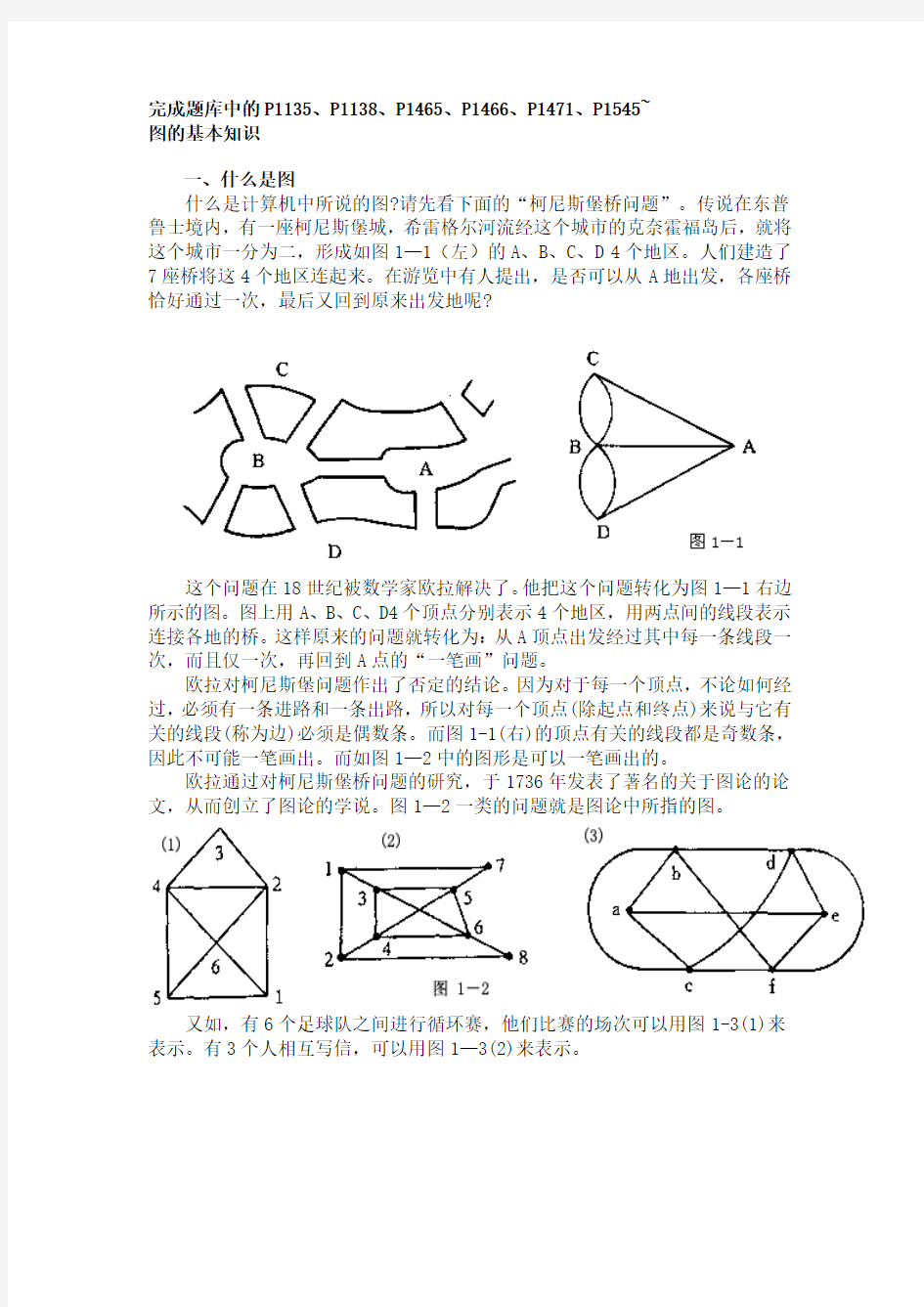
什么是计算机中所说的图?请先看下面的“柯尼斯堡桥问题”。传说在东普鲁士境内，有一座柯尼斯堡城，希雷格尔河流经这个城市的克奈霍福岛后，就将这个城市一分为二，形成如图1—1（左）的A、B、C、D 4个地区。人们建造了7座桥将这4个地区连起来。在游览中有人提出，是否可以从A地出发，各座桥恰好通过一次，最后又回到原来出发地呢?

这个问题在18世纪被数学家欧拉解决了。他把这个问题转化为图1—1右边所示的图。图上用A、B、C、D4个顶点分别表示4个地区，用两点间的线段表示连接各地的桥。这样原来的问题就转化为：从A顶点出发经过其中每一条线段一次，而且仅一次，再回到A点的“一笔画”问题。

欧拉对柯尼斯堡问题作出了否定的结论。因为对于每一个顶点，不论如何经过，必须有一条进路和一条出路，所以对每一个顶点(除起点和终点)来说与它有关的线段(称为边)必须是偶数条。而图1-1(右)的顶点有关的线段都是奇数条，因此不可能一笔画出。而如图1—2中的图形是可以一笔画出的。

欧拉通过对柯尼斯堡桥问题的研究，于1736年发表了著名的关于图论的论文，从而创立了图论的学说。图1—2一类的问题就是图论中所指的图。

又如，有6个足球队之间进行循环赛，他们比赛的场次可以用图1-3(1)来表示。有3个人相互写信，可以用图1—3(2)来表示。

从上面两个例子可看出，我们这里所说的图(graph)，与人们通常所熟悉的图，如圆、四边形、函数图象等是很不相同的。是指某些具体事物和这些事物之间的联系。如果我们用点来表示事物(如地点、队)，用线段来表示两事物之间的联系，那么一个图就是表示事物的点集和表示事物之间联系的线段集合所构成。其中线段仅表示两点的关系，它的长短与曲直是无关紧要的。例如图1-4中3

个图，被认为是同一个图。

图(Graph)是一种复杂的非线性结构。在人工智能、工程、数学、物理、化学、生物和计算机科学等领域中，图结构有着广泛的应用。奥林匹克信息学竞赛的许多试题，亦需要用图来描述数据元素间的联系。

二、图的基本概念

定义：图G定义为一个偶对(V，E)，记作G：(V，E)。其中

1)V是一个非空有限集合，它的元素称为顶点；

2)E也是一个集合，它是如下集合(它的元素称为边)的子集：

E∩{(a,b|a ∈ V，b ∈ V}

例如图4-1中的图有4个顶点，4条边。

或者定义：图G（Graph）是由顶点的集合V和边的集合E所组成的二元组，记作：

G =（V，E）

其中V是顶点的集合，E是边的集合。

（一）有向图和无向图

1．有向图

若图G中的每条边都是有方向的，则称G为有向图(Digraph)。在有向图中，一条有向边是由两个顶点组成的有序对，有序对通常用尖括号表示。有向边也称

为弧(Arc)，边的始点称为弧尾(Tail)，终点称为弧头(Head)。例如

i ，v

j

>表示

一条有向边，v

i 是边的始点(起点)，v

j

是边的终点。因此，

i

，v

j

>和

j

，v

i

>是

两条不同的有向边。下面(a)图中G

1

是一个有向图。图中边的方向是用从始点指

向终点的箭头表示的，该图的顶点集和边集分别为：V(G

1)={v

1

，v

2

，

v 3} E(G

1

)={

1

，v

2

>，

2

，v

1

>，

2

，v

3

>}

2．无向图

若图G中的每条边都是没有方向的，则称G为无向图(Undigraph)。无向图中

的边均是顶点的无序对，无序对通常用圆括号表示。例如无序对(v

i ，v

j

)和(v

j

，

v i )表示同一条边。下面(b)图中的G

2

和(c)图中的G

3

均是无向图，它们的顶点集

和边集分别为：

V(G

2)={v

1

，v

2

，v

3

，v

4

}

E(G

2)={(v

l

，v

2

)，(v

1

，v

3

)，(v

1

，v

4

)，(v

2

，v

3

)，(v

2

，v

4

)，(v

3

，v

4

)}

V(G

3)={v

1

，v

2

，v

3

，v

4

，v

5

，v

6

，v

7

}

E(G

3)={(v

1

，v

2

)，(v

l

，v

3

)，(v

2

，v

4

)，(v

2

，v

5

)，(v

3

，v

6

)，(v

3

，v

7

)}

3．图G的

顶点数n和边数e的关系

（1）若G是无向图，则0≤e≤n(n-1)/2

恰有n(n-1)/2条边的无向图称无向完全图(Undireet-ed Complete Graph) （2）若G是有向图，则0≤e≤n(n-1)。

恰有n(n-1)条边的有向图称为有向完全图(Directed Complete Graph)。

注意：完全图具有最多的边数。任意一对顶点间均有边相连。例如上面(b)图的G

2

就是具有4个顶点的无向完全图。

（二）图的边和顶点的关系

1.无向边和顶点关系

若(v

i ,v

j

)是一条无向边，则称顶点v

i

和v

j

互为邻接点(Adjacent)，或称v

i

和v

j 相邻接；并称(v

i

,v

j

)依附或关联(Incident)于顶点v

i

和v

j

，或称(v

i

，v

j

)与

顶点v

i 和v

j

相关联。例如上图（b）G

2

中：① 与顶点v

1

相邻接的顶点是v

2

，v

3

和v

4 ；② 关联于顶点v

2

的边是(v

1

，v

2

)，(v

2

，v

3

)和(v

2

，v

4

)

2．有向边和顶点关系

若

i ，v

j

>是一条有向边，则称顶点v

i

邻接到v

j

，顶点v

i

邻接于顶点v

j

；并

称边

i ，v

j

>关联于v

i

和v

j

或称

i

，v

j

>与顶点v

i

和v

j

相关联。例如在上图（a）

G 1中，关联于顶点v

2

的弧是

1

，v

2

>，

2

，v

1

>和

2

，v

3

>。

3．顶点的度(Degree)

（1）无向图中顶点v的度(Degree)

无向图中顶点v的度(Degree)是关联于该顶点的边的数目，记为D(v)。例如

上图（b）G

2中顶点v

1

的度为3

（2）有向图顶点v的度(InDegree)

有向图中，以顶点v为终点的边的数目称为v的入度(Indegree)，记为ID(v)。

例如在上图（a）G

1中顶点v

2

的人度为l。有向图中，以顶点v为始点的边的数

目，称为v的出度(Outdegree)，记为OD(v)。例如在上图（a）G

1中顶点v

2

的出

度为2。所以在有向图中，顶点v的度定义为该顶点的入度和出度之和，即

D(v)=ID(v)+OD(v)。例如在上图（a）G

1中顶点v

2

的人度为l，出度为2，则度为

3。

从上述我们可以得知，无论有向图还是无向图，顶点数n、边数e和度数之间有如下关系：

[例4.12]G是一个非连通无向图，共有28条边，则该图至少有个顶点。[解答]8个顶点的完全图共有28条边，再加一个孤立顶点使G成为非连通的。其他情况，由于点未充分利用必定多于9个。所以答案是9。

（三）子图

设G=(V，E)是一个图，若V'是V的子集，E'是E的子集，且E'中的边所关联的顶点均在V'中，则G'=(V'，E')也是一个图，并称其为G的子图(Subgraph)。

例如下面图（a）给出了有向图G

l 的若干子图；图（b）给出了无向图G

2

的若干

个子图。

再比如，设V'={v

1，v

2

，v

3

}，E'={(v

l

，v

2

)，(v

2

，v

4

)}，显然，V'属于V(G

2

)，

E'属于E(G

2)，但因为E'中序偶对(v

2

，v

4

)所关联的顶点v

4

不在V'中，所以(V'，

E')不是图，也就不可能是G

2

的子图。

（四）路径(Path)

1．无向图的路径

在无向图G中，若存在一个顶点序列v

p ,v

i1

，v

i2

,…，v

im

，v

q

，使得(v

p

，v

i1

)，

(v

i1，v

i2

)，…，(v

im

，v

q

)均属于E(G)，则称顶点v

p

到v

q

存在一条路径(Path)。

(a) (b)

2．有向图的路径

在有向图G中，路径也是有向的,它由E(G)中的有向边

p ，v

i1

>，

i1

，v

i2

>，…，

im ，v

q

>组成。

3．路径长度

路径长度定义为该路径上边的数目。4．简单路径

若一条路径上除了v

p 和v

q

可以相同外，其余顶点均不相同，则称此路径为一

条简单路径。例如在图G

2中顶点序列v

l

，v

2

，v

3

，v

4

是一条从顶点v

1

到顶点v

4

的

长度为3的简单路径。例如在图G

2中，顶点序列v

1

，v

2

，v

4

，v

1

，v

3

是一条从顶

点v

1到顶点v

3

的长度为4的路径，但不是简单路径；

5．简单回路或简单环(Cycle)

起点和终点相同(v

p =v

q

)的简单路径称为简单回路或简单环(Cycle)。例如图

G 2中，顶点序列v

1

，v

2

，v

4

，v

1

是一个长度为3的简单环。例如有向图G

1

中，顶

点序列v

1，v

2

，v

1

是一长度为2的有向简单环。

6．有根图和图的根

在一个有向图中，若存在一个顶点v，从该顶点有路径可以到达图中其它所有顶点，则称此有向图为有根图，v称作图的根。

（五）连通图和连通分量

1．顶点间的连通性

在无向图G中，若从顶点v

i 到顶点v

j

有路径(当然从v

j

到v

i

也一定有路径)，

则称v

i 和v

j

是连通的。

2．连通图

若V(G)中任意两个不同的顶点v

i 和v

j

都连通(即有路径)，则称G为连通图

(Con-nected Graph)。例如图G

2，和G

3

是连通图。

3．连通分量

无向图G的极大连通子图称为G的连通分量(Connected Component)。注意：任何连通图的连通分量只有一个，即是其自身；另外非连通的无向图有多个连通

分量。例如下图中的G

4是非连通图，它有两个连通分量H

1

和H

2

。

（六）强连通图和强连通分量1．强连通图

有向图G中，若对于V(G)中任意两个不同的顶点v

i 和v

j

，都存在从v

i

到v

j

以及从v

j 到v

i

的路径，则称G是强连通图。

2．强连通分量

有向图的极大强连通子图称为G的强连通分量。强连通图只有一个强连通分

量，即是其自身。非强连通的有向图有多个强连分量。例如下图中的G 1不是强连通图，因为v 3到v 2没有路径，但它有两个强连通分量，如右图所示。

（七）图的存储结构

图的存储方法有很多，我们这里只介绍图的邻接矩阵和邻接表两种表示法。 1、邻接矩阵（数组）

在图的邻接矩阵表示法中：

① 用邻接矩阵表示顶点间的相邻关系 ② 用一个顺序表来存储顶点信息

设G=(V ，E)是具有n 个顶点的图，则G 的邻接矩阵是具有如下性质的n 阶方阵，其规模为n ×n ：

例如下图中无向图G 5和有向图G 6的邻接矩阵分别为A l 和A 2。

1（或权）， （vi ,vj ）∈E ； A[i,j]= 0（或∞）， （vi ,vj ）∈E ；

图的类型定义：

Cconst n=< 图的顶点上限 >

Type adj=0..1;

adjm=array[1..n,1..n]OF adj;{邻接矩阵}

graph=RECORD

V：array[1..n]OF Vtype；{顶点元素}

E：adjm；

END；

2、邻接表（链表）

邻接表是图的一种链式存储结构。在邻接表中，对图的每一个顶点建立一个单链表，第i个单链表中的结点表示依附于顶点Vi的边。每个结点由2个域组成：

顶点域——指示与顶点Vi邻接的点的序号；

链域——指向依附于顶点Vi的下一条边所对应的结点。

—>

—>

—>

—>

—>

一个图的邻接表存储结构可形式地说明如下：

TYPE

arcptr=^arcnode;

arcnode=RECORD

adjvex:1..num; {邻接点域}

next:atrcptr; {链域}

END;

vexnode=RECORD

vertex:vertype; {顶点信息}

firstatc:arcptr

END

adj1=ARRAY[1..num] of vexnode;

图的应用

1、一笔画问题

图的典型应用是一笔画问题，其他应用将在图论算法中涉及。

[例题] 编程找出图1－2（1）的一笔画路线。

[分析与解]：

(1)首先用邻接矩阵来表示图：如果i,j两点间有线段连接则值为1，否则为0。

0 1 0 0 1 1

1 0 1 1 0 1

0 1 0 1 0 0

O 1 1 0 1 1

1 0 0 1 0 1

1 1 0 1 1 0

可用数组常量links[i,j] 表示，即：

const links:array[1..n, 1..n] OF Integer=

((0,1,0,0,1,1), (1,0,1,1,0,1),(0,1,0,1,0,0),

(O,1,1,0,1,1),(1,0,0,1,0,1), (1,1,0,1,1,0));

(2)计算每个点的度数存dgr[i]中，如对于第i个顶点，可这样统计：

for j:=1 to n do dgr[i]:=dgr[i]+links[i,j];

sum:=sum+dgr[i];

(3)统计奇点的个数，即dgr中有几个奇数，存odt中。

if odd(dgr[i]) then odt:=odt+1;

start;=i;

(4)如果odt>2则无解，否则从一个奇点开始搜索路线，其算法如下

[程序清单]

Program postal_route;

const n = 6;

links:array[1..n, 1..n] OF Integer=

((0,1,0,0,1,1), (1,0,1,1,0,1),

(0,1,0,1,0,0), (O,1,1,0,1,1),

(1,0,0,1,0,1), (1,1,0,1,1,0));

var

dgr: array[1..n] of integer;

i, j, r, sum, odt, start, nowd: integer;

Procedure find_degree;

Begin

sum:=0; odt:=0; start:=1;

For i:= 1 to n Do

Begin

dgr[i]:= 0;

For j:= 1 to n do dgr[i]:= dgr[i] + links[i,j]; sum:= sum + dgr[i];

If odd(dgr[i]) Then

Begin odt := odt + 1; start:= i End

End;

End;

{ main code .... }

BEGIN

Find_degree

if odt>2 Then

Begin writeln ('no sulution . ');exit End;

Nowd:= start;

write(start);

repeat

r:=0;

repeat

r:=r+1;

until (links[nowd,r]>0) and ((dgr[r]>1) or ((dgr[r]=1) and (sum=2)));

links[nowd,r]:=0; links[r,nowd]:=0; sum:=sum-2;

dec(dgr[nowd]); dec(dgr[r]);

nowd :=r;

write('->',r);

until sum = 0;

writeln; readln

END.

运行结果为：

5->1->2->3->->4->2->6->4->5->6->1

2、图的遍历

给出一个图G和其中任意一个结点V

0，从V

出发系统地访问G中所有结点，

每一个结点被访问一次，这就叫图的遍历。遍历图的结果是按访问顺序将结点排成一个线性序列。通常有两种遍历方法：深度优先搜索和广度优先搜索，他们对无向图和有向图都适用。

1．深度优先搜索

深度优先搜索类似于树的前序遍历，是树的前序遍历的推广。假设初始时所

有结点未曾被访问，深度优先搜索从某个结点V

0出发，然后依次访问从V

的未

被访问的邻接点出发深度优先搜索遍历图，直至图中所有和V

有路径相连的结点都被访问到。若此时图中尚有结点未被访问，则以另选一个未曾访问的结点为起始点，重复上述过程，直至图中所有结点都被访问为止。换句话说，深度优先搜

索遍历图的过程是以V

0为起始点，由左而右，依次访问由V

出发的每条路径。

例如，上图G6，从V

2

出发，按深度优先搜索得到的序列是：

V 2→V

1

→V

→V

4

→V

3

。

深度优先在搜索过程中也为结点着色以表示结点的状态。每个顶点开始均为

白色，搜索中被发现时置为灰色，结束时又被置成黑色(即当其邻接表被完全检索之后)。这一技巧可以保证每一顶点搜索结束时只存在于一棵深度优先树上，因此这些树都是分离的。

除了创建一个深度优先森林外，深度优先搜索同时为每个结点加盖时间戳。每个结点v有两个时间戳：当结点v第一次被发现(并置成灰色)时记录下第一个时间戳d[v]，当结束检查v的邻接表时(并置v为黑色)记录下第二个时间截

f[v]。许多图的算法中都用到时间戳，他们对推算深度优先搜索进行情况是很有帮助的。

下列过程DFS记录了何时在变量d[u]中发现结点u以及何时在变量f[u]中完成对结点u的检索。这些时间戳为1到2|V|之间的整数，因为对每一个v中结点都对应一个发现事件和一个完成事件。对每一顶点u，有

d[u]

在时刻d[u]前结点u为白色，在时刻d[u]和f[u]之间为灰色，以后就变为黑色。

下面的伪代码就是一个基本的深度优先搜索算法，输人图G可以是有向图或无向图，变量time是一个全局变量，用于记录时间戳。

procedure DFS(G);

begin

1 for 每个顶点u∈V[G] do

begin

2 color[u]←White;

3 π[u]←NIL;

end;

4 time←0;

5 for 每个顶点u∈V[G] do

6 if color[u]=White

7 then DFS_Visit(G,u);

end;

procedure DFS_Visit(G,u);

begin

1 color[u]←Gray; Δ白色结点u已被发现

2 d[u]←time←time+1;

3 for 每个顶点v∈Adj[u] do Δ探寻边(u,v)

4 if color[v]=White

then begin

5 π[v]←u;

6 DFS_Visit(G,v);

end;

7 color[u]←Black; Δ完成后置u为黑色

8 f[u]←time←time+1;

end;

图2说明了DFS在图1所示的图上执行的过程。被算法探寻到的边要么为阴影覆盖 (如果该边为树枝)，要么成虚线形式 (其他情况)。对于非树枝的边，分别标明B(或F)以表示反向边、交叉边或无向边。我们用发现时刻Z完成时刻的形式对结点加盖时间戳。

图1 一个有向图图

图2 深度优先搜索算法DFS在有向图图1上的执行过程

过程DFS执行如下。第1-3行把所有结点置为白色，所有π域初始化为NIL。第4行复位全局变量time，第5-7行依次检索V中的结点，发现白色结点时，调用DFS_Visit去访问该结点。每次通过第7行调用DFS_Visit时，结点u就成为深度优先森林中一棵新树的根，当DFS返回时，每个结点u都对应于一个发现时刻d[u]和一个完成时刻f[u]。

每次开始调用DFS_Visit(u)时结点u为白色，第1行置u为灰色，第2行使全局时间变量增值并存于d[u]中，从而记录下发现时刻d[u]，第3-6行检查和u相邻接的每个顶点v，且若v为白色结点，则递归访问结点v。在第3行语句中考虑到每一个结点v∈Adj[u]时，我们可以说边(u,v)被深度优先搜索探寻。最后当以u为起点的所有边都被探寻后，第7-8行语句置u为黑色并记录下完成时间f[u]。

算法DFS运行时间的复杂性如何？DFS中第1-2行和5-7行的循环占用时间为O(V),这不包括执行调用DFS_Visit过程语句所耗费的时间。事实上对每个顶点v∈V，过程DFS_Visit仅被调用一次，因为DFS_Visit仅适用于白色结点且过程首先进行的就是置结点为灰色，在DFS_Visit(v)执行过程中，第3-6行的循环要执行|Adj[v]|次。因为∑

v∈V

|Adj[v]| =θ(E)，因此执行过程DFS_Visit 中第2-5行语句占用的整个时间应为θ(E)。所以DFS的运行时间为θ(V+E)。

2．广度优先搜索

广度优先搜索算法（又称宽度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和广度优先搜索类似的思想。

广度优先搜索类似于树的按层次遍历的过程。假设从图中某结点V

出发，在

访问了V

0之后依次访问V

的各个未曾访问的邻接点，然后分别从这些邻接点出

发按广度优先搜索的顺序遍历图，直至图中所有可被访问的结点都被访问到。若此时图中尚有结点未被访问，则以另选一个未曾访问的结点为起始点，重复上述过程，直至图中所有结点都被访问为止。换句话说，广度优先搜索遍历图的过程

是以V

0为起始点，由近及远，依次访问和V

有路径相连且路径长度为1，2，3，……

的结点。例如，上图G6，从V

2

出发，按广度优先搜索得到的序列是：

V 2→V

1

→V

3

→V

→V

4

。

之所以称之为广度优先算法，是因为算法自始至终一直通过已找到和末找到

顶点之间的边界向外扩展，就是说，算法首先搜索和s距离为k的所有顶点，然后再去搜索和S距离为k+l的其他顶点。

为了保持搜索的轨迹，广度优先搜索为每个顶点着色：白色、灰色或黑色。算法开始前所有顶点都是白色，随着搜索的进行，各顶点会逐渐变成灰色，然后成为黑色。在搜索中第一次碰到一顶点时，我们说该顶点被发现，此时该顶点变为非白色顶点。因此，灰色和黑色顶点都已被发现，但是，广度优先搜索算法对它们加以区分以保证搜索以广度优先的方式执行。若(u,v)∈E且顶点u为黑色，

那么顶点v要么是灰色，要么是黑色，就是说，所有和黑色顶点邻接的顶点都已被发现。灰色顶点可以与一些白色顶点相邻接，它们代表着已找到和未找到顶点之间的边界。

在广度优先搜索过程中建立了一棵广度优先树，起始时只包含根节点，即源顶点s.在扫描已发现顶点u的邻接表的过程中每发现一个白色顶点v，该顶点v 及边(u,v)就被添加到树中。在广度优先树中，我们称结点u是结点v的先辈或父母结点。因为一个结点至多只能被发现一次，因此它最多只能有--个父母结点。相对根结点来说祖先和后裔关系的定义和通常一样：如果u处于树中从根s到结点v的路径中，那么u称为v的祖先，v是u的后裔。

图1展示了用BFS在例图上的搜索过程。黑色边是由BFS产生的树枝。每个节点u内的值为d[u]，图中所示的队列Q是while循环中每次迭代起始时的队列。队列中每个结点下面是该结点与源结点的距离。

图1 BFS在一个无向图上的执行过程

下面的广度优先搜索过程BFS假定输入图G=(V,E)采用邻接表表示，对于图中的每个顶点还采用了几种附加的数据结构，对每个顶点u∈V，其色彩存储于变量color[u]中，结点u的父母存于变量π[u]中。如果u没有父母(例如u=s 或u还没有被检索到)，则π[u]=NIL，由算法算出的源点s和顶点u之间的距离存于变量d[u]中，算法中使用了一个先进先出队列Q来存放灰色节点集合。其中head[Q]表示队列Q的队头元素，Enqueue(Q,v)表示将元素v入队，Dequeue(Q)表示对头元素出队；Adj[u]表示图中和u相邻的节点集合。

procedure BFS(G,S);

begin

1. for 每个节点u∈V[G]-{s} do

begin

2. color[u]←White; {置每个结点为白色}

3. d[u]←∞; {置d[u]为无穷大}

4. π[u]←NIL; {每个结点的父母置为NIL}

end;

5. color[s]←Gray; {置源结点S为灰色}

6. d[s]←0; {初始化d[s]为0}

7. π[s]←NIL; {置源结点的父母结点为NIL}

8. Q←{s} {初始化队列为0}

9. while Q≠φ do

begin

10. u←head[Q]; {确定队列头的灰色结点为u}

11. for 每个节点v∈Adj[u] do

12. if color[v]=White then

begin {发现结点的处理}

13. color[v]←Gray; {置为灰色}

14. d[v]←d[v]+1; {距离+1}

15. π[v]←u; {把u记为该节点的父母}

16. Enqueue(Q,v); {放在队列Q的队尾}

end;

17. Dequeue(Q); {使u 弹出队列并置成黑色} 18. color[u]←Black; end; end;

过程BFS 按如下方式执行，第1-4行置每个结点为白色，置d[u]为无穷大，每个结点的父母置为NIL ，第5行置源结点S 为灰色，即意味着过程开始时源结点已被发现。第6行初始化d[s]为0，第7行置源结点的父母结点为NIL ，第8行初始化队列0，使其仅含源结点s ，以后Q 队列中仅包含灰色结点的集合。 程序的主循环在9-18行中，只要队列Q 中还有灰色结点，即那些已被发现但还没有完全搜索其邻接表的结点，循环将一直进行下去。第10行确定队列头的灰色结点为u 。第11-16行的循环考察u 的邻接表中的每一个顶点v 。如果v 是白色结点，那么该结点还没有被发现过，算法通过执行第13-16行发现该结点。首先它被置为灰色，距离d[v]置为d[u]+1，而后u 被记为该节点的父母，最后它被放在队列Q 的队尾。当结点u 的邻接表中的所有结点都被检索后，第17-18行使u 弹出队列并置成黑色。

[例4.13]如图有向图，试给出（1）邻接矩阵（2）强连通分量（3）从①出发的深度优先遍历序列（4）从⑥出发的广度优先遍历序列

[解答]（1）邻接矩阵：?

?

?

???

????

?????

????

?010010001011000000111000

000101001000

（2）强连通分量：在有向图G 中，如果对于每一对vi ，vj ∈V （顶点集），

且vi ≠vj ，从vi 道vj 和从vj 的vi 都存在路径，则称G 是强连通图。有向图中的极大强连通子图称作有向图的强连通分量。由

此得到强连通分量如图说示。

（3）从①出发的深度优先遍历序列可以为：①④②③⑤⑥。 （4）从⑥出发的广度优先遍历序列可以为： ⑥②⑤①③④。（注意（3）（4）答案不唯一） 小结：

1、顶点数n 和边数e 的关系

（1）若G 是无向图，则0≤e≤n(n -1)/2

恰有n(n-1)/2条边的无向图称无向完全图(Undireet-ed Complete Graph) （2）若G 是有向图，则0≤e≤n(n -1)。

恰有n(n-1)条边的有向图称为有向完全图(Directed Complete Graph)。

①

②

③

④

⑤ ⑥ ① ② ③ ④

⑤ ⑥

【本章练习】 一、选择题

1.如图说示，在下面的5个序列中符合深度优先遍历的序列

有 个。 (1)aebdfc (2)acfdeb (3)aedfcb (4)aefdcb (5)aefdbc

A.5个

B.4个

C.3个

D.2个 2.设无向图的顶点个数为n ，则该无向图最多有 条边。 A.n-1 B.n(n-1)/2 C.n(n+1)/2 D.0

E.n 2

3.一个图中包含有k 个连通分量，若按深度优先（DFS ）搜索方法访问所有结点，则必须调用 次深度优先遍历算法。 A.k B.1 C.k-1 D.k+1

4.具有n 个顶点的有向图最多有 条边。 A.n B.n(n-1) C.n(n+1) D.n 2

5.一个n 个顶点的连通无向图，其边的个数至少为 。 A.n-1 B.n C.n+1 D.nlog 2n

6.在一个具有n 个顶点的有向图中，若所有顶点的出度之和为s ，则所有顶点的入度之和为 。

A.s

B.s-1

C.s+1

D.n

7.在一个无向图中，若两个顶点之间的路径长度为k ，则该路径上的顶点数为 。

A.k

B.k+1

C.k+2

D.2k

8.一个有n 个顶点的无向连通图，它说包含的连通分量个数为 。 A.0 B.1 C.n D.n+1

二、问题求解

1. 无向图G 有16条边，有3个4度顶点、4个3度顶点，其余顶点的度均小于3，则G 至少 个顶点。

三、程序填空 求关键路径

设有一个工程网络如下图表示(无环路的有向图)：

其中，顶点表示活动，①表示工程开始，⑤表示工程结束(可变，用N 表示)，边上的数字表示活动延续的时间。

如上图中，活动①开始5天后活动②才能开始工作，而活动③则要等①、②完成之后才能开始，即最早也要7天后才能工作。

在工程网络中，延续时间最长的路径称为关键路径。上图中的关键路径为：①—②—③—④—⑤共18天完成。 关键路径的算法如下：

a b c d e f

1.数据结构：

R[1..N，1..N]OF INTEGER；表示活动的延续时间，若无连线，则用-1表示；

EET[1..N] 表示活动最早可以开始的时间

ET[1..N] 表示活动最迟应该开始的时间

关键路径通过点J，具有如下的性质：EET[J]=ET[J]

2.约定：

结点的排列已经过拓扑排序，即序号前面的结点会影响序号后面结点的活动。程序清单：

PROGRAM GAO7_6；

VAR I，J，N，MAX，MIN，W，X，Y：INTEGER；

R：ARRAY[1..20，1..20] OF INTEGER；

EET，ET：ARRAY[1..20] OF INTEGER；

BEGIN

READLN(N)

FOR I:=1 TO N DO

FOR J:=1 TO N DO

R[I，J]:=-1；

READLN(X，Y，W)；{输入从活动X到活动Y的延续时间，以0为结束} WHILE X<>0 DO

BEGIN

R[X，Y]:=W；①

END；

EET[1]：=0；{认为工程从0天开始}

FOR I：=2 TO N DO

BEGIN

MAX:=0；

FOR J:=1 TO N DO

IF R[J，I]<>-1 THEN

IF ②THEN MAX:=R[J，I]+EET[J]；

EET[I]:=MAX；

END；

③

FOR I：=N-1 DOWNTO 1 DO

BEGIN

MIN：=10000；

FOR J：=1 TO N DO

IF R[I，J]<>-1 THEN

IF ④THEN MIN：=ET[J] - R[I，J]；

ET[I]：=MIN；

END；

WRITELN(EET[N])；

FOR I：=1 TO N -1 DO

IF ⑤THEN WRITE(I，'→')；