数字信号处理答案10

Chapter 10 Solutions10.1 (a) The impulse response is given by h[n] = –0.8h[n –1] + 0.1h[n –2] + δ[n]. The first ten samples are listed in the table.(b) The impulse response contains an infinite number of non-zero terms.10.3 (a)(i) Without pre-warping, the transfer function for the analog filter is15708s 15708)2500(2s )2500(2s )s (H 1p 1p +=π+π=ω+ω=The bilinear transformation 1z 1z f 2s S +-=gives11z00921.01)z1(4954.0157081z 1z 1600015708)z (H ---+=++-=(ii)The analog frequency 2.5 kHz is converted to a digital frequency Ωp1 =8000/)2500(2π =1.9635 rads. 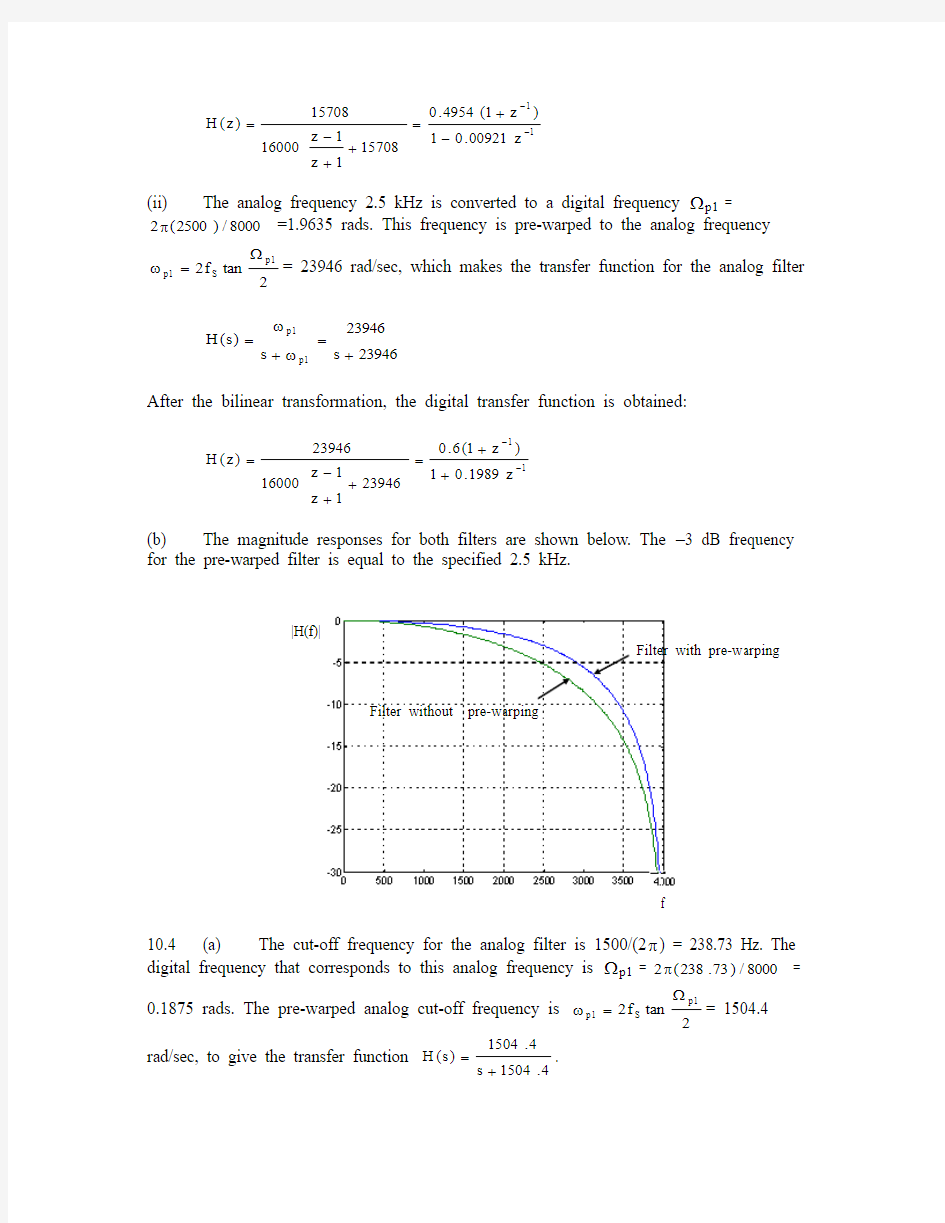This frequency is pre-warped to the analog frequency2tanf 21p S 1p Ω=ω= 23946 rad/sec, which makes the transfer function for the analog filter23946s 23946s )s (H 1p 1p +=ω+ω=After the bilinear transformation, the digital transfer function is obtained:11z1989.01)z1(6.0239461z 1z 1600023946)z (H --++=++-=(b) The magnitude responses for both filters are shown below. The –3 dB frequency for the pre-warped filter is equal to the specified 2.5 kHz.10.4 (a) The cut-off frequency for the analog filter is 1500/(2π) = 238.73 Hz. The digital frequency that corresponds to this analog frequency is Ωp1 = 8000/)73.238(2π = 0.1875 rads. The pre-warped analog cut-off frequency is 2tan f 21p S 1p Ω=ω= 1504.4rad/sec, to give the transfer function 4.1504s 4.1504)s (H +=.Filter with pre-warping |H(f)| f(b) Use the bilinear transformation to get the digital transfer function11z8281.01)z 1(0859.04.15041z 1z 160004.1504)z (H ---+=++-=(c) The difference equation is y[n] = 0.8281y[n –1] + 0.0859x[n] + 0.0859x[n –1]. (d)The frequency response is Ω-Ω--+=Ωj j e8281.01)e 1(0859.0)(H . The magnitude responsemay be found by taking the magnitudes of this expression for several values of Ω. It is plotted below against frequency in Hz.(e) The magnitude for the analog transfer function is224.15044.1504)(H +ω=ωThe shape of the digital filter may be found by substituting 2tan f 2S Ω=ω:2222S 4.15042tan 160004.15044.15042tan f 24.1504)(H +⎪⎭⎫ ⎝⎛Ω=+⎪⎭⎫ ⎝⎛Ω=ΩThis function may be plotted for various values of Ω. The magnitude response is plotted below against digital frequency in rads. When digital frequencies are converted to frequencies in Hz, the plot becomes identical to the one in part (d).10.5 The –3 dB frequency for this filter is 1 kHz. This is the edge of the pass band. The stop band edge can chosen at any convenient place. For example, the gain at 3 kHz is about –46 dB. The stop band ripple is given by 20log δs = –46, or δs = 0.005. The digital frequencies at the edges of the pass band and stop band areΩp1 = π=π=π25.0800010002f f 2S1p radiansΩs1 =π=π=π75.0800030002f f 2S1s radiansωp1 = 4.66272tanf 21p S =Ω rad/secωs1 = 4.386272tanf 21s S =Ω rad/secThe order for the filter is10.6 The stop band attenuation gives 20log δs = –28, or δs = 0.0398. Ωp1 = π=π=π542.02400065002f f 2S1p radians34.66274.38627log 21)005.0(1log log 211log n 21p 1s 2s =⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ≥|H(Ωs1 =π=π=π667.02400080002f f 2S1s radiansωp1 = 4.547912tanf 21p S =Ω rad/secωs1 = 1.832392tanf 21s S =Ω rad/secThe order for the filter can be calculated usingso an order of 8 should be chosen. For this order, the magnitude response for the analog filter is given by14.54791111)(H 16n21p +⎪⎭⎫ ⎝⎛ω=+⎪⎪⎭⎫ ⎝⎛ωω=ωTherefore, the transfer function for the digital filter is14.547912tan 48000114.547912tan f 21)(H 1616S+⎪⎪⎪⎪⎭⎫⎝⎛Ω=+⎪⎪⎪⎪⎭⎫⎝⎛Ω=ΩThe plot of |H(Ω)| versus Ω is the same as the plot of |H(f)| versus f, except that, along the horizontal axis, digital frequencies between 0 and π radians are converted tofrequencies between 0 and 12000 Hz (half the sampling rate). The magnitude response is shown below. The eighth order filter matches the specifications.7.74.547911.83239log 21)0398.0(1log log 211log n 21p 1s 2s =⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ≥10.7 The stop band attenuation gives 20log δs = –35, or δs = 0.01778.Ωp1 = π=π=π625.0800025002f f 2S1p radiansΩs1 =π=π=π95.0800038002f f 2S1s radiansωp1 = 239462tanf 21p S =Ω rad/secωs1 = 2032992tanf 21s S =Ω rad/secThe order for the filter can be calculated usingso an order of 2 should be chosen.10.8 The 600 Hz transition width puts the stop band edge at 1.9 kHz. The digital pass band edge frequencies areΩp1 = π=π=π26.01000013002f f 2S1p radians|H(f)|f9.123946203299log 21)01778.0(1log log 211log n 21p 1s 2s =⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ≥Ωs1 =π=π=π38.01000019002f f 2S1s radiansωp1 = 8.86542tanf 21p S =Ω rad/secωs1 = 0.135922tanf 21s S =Ω rad/secSince the order for the filter is 5,This expression gives96.111log 2s =⎪⎪⎭⎫⎝⎛-δor,3.91101196.12s==-δwhich gives δs = 0.1047, which in turn means a stop band gain of 20log(0.1047) = –19.6 dB. Thus, the stop band attenuation is 19.6 dB.10.9 With 16 kHz sampling, an analog frequency of 3.5 kHz corresponds to a digital frequency of π=π=π=Ω4375.01600035002f f 2S'p rads. Pre-warping gives 'p ω =7.262612tanf 2'p S =Ω rad/sec. The analog transfer function for a first order high passfilter is obtained by transforming a first order low pass transfer function such as⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-δ=⎪⎪⎭⎫⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ==8.86540.13592log 211log log 211log 5n 2s 1p 1s 2s5.2360s 5.2360s )s (H pp L +=ω+ω=(Any low pass filter with a known cut-off frequency will do.) The high pass transfer function can be found as follows:()()⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛ωω=s 7.262615.2360H s H )s (H L 'pp L H ()()7.26261s s 5.2360s7.262615.23605.2360+=+⎪⎭⎫⎝⎛=The digital counterpart is given by the bilinear transformation:()11H z0985.01z 15492.07.262611z 1z 320001z 1z 32000)z (H ----=++-+-=The difference equation for the high pass filter is y[n] = 0.0985y[n –1] + 0.5492x[n] – 0.5492x[n –1].10.10 A stop band attenuation of 40 dB gives 20log δs = –40 dB, which means δs = 0.01. The low pass prototype for the high pass filter will have a cut-off at f S /2 – 9 = 22 – 9 = 13 kHz. The pass band frequencies are:Ωp1 = π=π=π591.044000130002f f 2S1p radiansωp1 = 1175892tanf 21p S =Ω rad/sec(a)With an order n = 3,⎪⎭⎫⎝⎛ω⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ==117589log 21)01.0(1log log 211log 3n 1s 21p 1s 2s⎪⎭⎫ ⎝⎛ω117589log 1s = 0.667ωs1 = 546219This result can be used to solve for f s1:546219 = 2tan f 21s S Ω411.1207.6tan211s ==Ω-Ωs1 = 2.822 = S1s f f 2πso 748.192f 822.2f S1s =π= kHz. The transition width is 19748 – 13000 = 6748 Hz.(b) With an order n = 6,⎪⎭⎫⎝⎛ω⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ==117589log 21)01.0(1log log 211log 6n 1s 21p 1s 2s ⎪⎭⎫ ⎝⎛ω117589log 1s = 0.333ωs1 = 253143This result can be used to solve for f s1:253143 = 2tanf 21s S Ω667.01s 10117589=ω207.62tan1s =Ω333.01s 10117589=ω877.22tan1s =Ω236.1877.2tan211s ==Ω-Ωs1 = 2.472 = S1s f f 2πso 311.172f 472.2f S1s =π=kHz. The transition width is 17311 – 13000 = 4311 Hz.10.11 The transfer function for a second order low pass analog Butterworth filter is:21p 1p 221p s 2s )s (H ω+ω+ω=The cut-off frequency givesΩp1 = π=π=π625.0800025002f f 2S1p radiansωp1 = 239462tanf 21p S =Ω rad/secfor an analog transfer function573410916s 33865s 573410916)s (H 2++=The bilinear transformation1z 1z 16000s +-=converts this transfer function to a digital transfer function:5734109161z 1z 16000338651z 1z 16000573410916)z (H 2+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-=2121z20971.0z46295.01z41817.0z83634.041817.0----++++=10.12 (a) An FIR design for this filter requires a Hanning window with N =3.32f S /T.W.= 3.32(8000)/(1500–1000) = 53.1 or 53 terms. This filter requires 53 filter coefficients. (b) The stop band attenuation gives 20log δs = –44, or δs = 0.00631.Ωp1 = π=π=π25.0800010002f f 2S1p radiansΩs1 =π=π=π375.0800015002f f 2S1s radiansωp1 = 66272tanf 21p S =Ω rad/secωs1 = 106912tanf 21s S =Ω rad/secThe order for the filter can be calculated usingso an order of 11 should be chosen. For this order, 2(11) + 1 = 23 filter coefficients are required, many fewer than the FIR design.10.13 The gain at the edge of the pass band for this Chebyshev filter is –2 dB, which means 20log(1–δp ) = –2, or δp = 0.2057. The pass band edge is located at 2 kHz. The stop band edge may be located at any convenient point, perhaps at 3 kHz, where the gain is about –46 dB. Since 20log δs = –46, or δs = 0.005.()()7649.012057.01111122p=--=-δ-=ε()0.2001005.011122s=-=-δ=δ6.10662710691log 21)00631.0(1log log 211log n 21p 1s 2s =⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ≥The digital frequencies at the edges of the pass and stop bands are:Ωp1 = π=π=π4.01000020002f f 2S1p radiansΩs1 =π=π=π6.01000030002f f 2S1s radiansωp1 = 9.145302tanf 21p S =Ω rad/secωs1 = 6.275272tanf 21s S =Ω rad/secThe order for the filter should be99.49.145306.27527cosh 7649.00.200coshcoshcosh n 111p 1s 11=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛ωω⎪⎭⎫ ⎝⎛εδ≥---- or 510.14 (a) The Chebyshev filter has a gain at the edge of the pass band of –0.5 dB, which means 20log(1–δp ) = –0.5, or δp = 0.0559. The pass band edge is located at 10 kHz. The stop band edge is located at 12 kHz, where the gain is about –20 dB. Since 20log δs = –20, or δs = 0.1.()()3492.010559.01111122p=--=-δ-=ε()95.911.011122s=-=-δ=δThe digital frequencies at the edges of the pass and stop bands are:Ωp1 = π=π=π625.032000100002f f 2S1p radiansΩs1 =π=π=π75.032000120002f f 2S1s radiansωp1 = 8.957822tanf 21p S =Ω rad/secωs1 = 7.1545092tanf 21s S =Ω rad/secThe order for the filter should be83.38.957827.154509cosh 3492.095.9coshcoshcosh n 111p 1s 11=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛ωω⎪⎭⎫ ⎝⎛εδ≥---- or 4(b) The magnitude response for a 4th order analog Chebyshev Type I filter is given by()⎪⎭⎫⎝⎛ω+=⎪⎪⎭⎫⎝⎛ωωε+=ω8.95782C 3492.011C 11)(H 2421p 2n2The filter shape for the digital filter is given by⎪⎪⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛Ω+=⎪⎪⎪⎪⎭⎫⎝⎛ω⎪⎭⎫ ⎝⎛Ωε+=Ω8.957822tan 64000C 1219.0112tan f 2C 11)(H 241p S 2n2⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛Ω+=2tan 6682.0C 1219.01124where⎩⎨⎧=--))x (cosh 4cosh())x (cos 4cos()x (C 114 1 |x |1|x |>≤This function can be computed for various values of Ω.The results are shown below, where digital frequencies have been converted to frequencies in Hz using Sf f 2π=Ω. The pass band edge occurs at 10 kHz with a gain of –0.5 dB, as expected. The stop gain gain of –20 dB is achieved slightly before 12 kHz because the order was rounded up to 4.10.15 For both filters, the digital frequencies at the edges of the pass and stop bands are:Ωp1 = π=π=π64.01500048002f f 2S1p radiansΩs1 =π=π=π72.01500054002f f 2S1s radians|H(f)|fωp1 = 472722tanf 21p S =Ω rad/secωs1 = 637532tanf 21s S =Ω rad/sec(a) Note that the pass band ripple for the filter is chosen so that a Butterworth design is possible. The order for the Butterworth filter isso an order of 8 should be chosen. (b) For the Chebyshev version:()()9975.01292.01111122p=--=-δ-=ε()46.12108.011122s=-=-δ=δ96.34727263753cosh 9975.046.12coshcoshcosh n 111p 1s 11=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛ωω⎪⎭⎫ ⎝⎛εδ≥----so an order of 4 should be chosen. Note that the order required for the Chebyshev filter is lower than that required for the Butterworth filter.10.16 The Chebyshev filter has a pass band ripple of –0.5 dB, which means 20log(1–δp ) = –0.5, or δp = 0.0559. Since the center frequency is 5 kHz and the width of the pass band is 1.6 kHz, the pass band edges are located at 4.2 kHz and 5.8 kHz. Because of the 400 Hz transition width, the stop band edges are located at 3.8 kHz, and 6.2 kHz, where the gain is –35 dB. Since 20log δs = –35, or δs = 0.01778.()()3492.010559.01111122p=--=-δ-=ε4.84727263753log 21)08.0(1log log 211log n 21p 1s 2s =⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛ωω⎪⎪⎭⎫ ⎝⎛-δ≥()23.56101778.011122s=-=-δ=δThe low pass prototype for this band pass filter has its pass band edge at (5.8 – 5) = 0.8 kHz. The transition width is 400 Hz, so the stop band is located at 1.2 kHz. Thus, the digital frequencies at the edges of the pass and stop bands are:Ωp1 = π=π=π107.0150008002f f 2S1p radiansΩs1 =π=π=π16.01500012002f f 2S1s radiansωp1 = 3.50902tanf 21p S =Ω rad/secωs1 = 7.77022tanf 21s S =Ω rad/secThe order for the filter should be9.53.50907.7702cosh 3492.023.56coshcoshcosh n 111p 1s 11=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛ωω⎪⎭⎫ ⎝⎛εδ≥---- or 610.17 The high pass filter may be obtained from an arbitrary first order low pass filter such as5.2360s 5.2360s )s (H pp L +=ω+ω=This low pass filter with cut-off ωp = 2360.5 rad/sec may be converted to a high passfilter with cut-off 'p ω using the conversion⎪⎪⎭⎫⎝⎛ωω=s H )s (H 'pp L HThe high pass cut-off of 3 kHz gives:'p Ω = π=π=π75.0800030002f f 2Sl radians'p ω= 4.386272tanf 21p S =Ω rad/secThe conversion formula becomes⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛ωω=s 7.91179977H s H )s (H L 'pp L HThe transfer function for the analog filter is4.38627s s5.2360s 7.911799775.2360)s (H H +=+⎪⎭⎫⎝⎛=The bilinear transformation 1z 1z 160001z 1z f 2S +-=+- produces the digital transfer function: 11z 4142.01)z 1(2929.04.386271z 1z 160001z 1z 16000)z (H --+-=+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-=10.18 The lower cut-off frequency is Ωl = =π8000100020.25π rads , or ωl =4.6627225.0tan f 2S =π rad/sec. The upper cut-off frequency will be Ωu ==π8000150020.375π rads, or ωu = 9.106902375.0tanf 2S =π rad/sec after pre-warping. Theband pass filter may be obtained from an arbitrary first order low pass filter such as5.2360s 5.2360s )s (H pp L +=ω+ω=The transfer function of the band pass filter may be obtained by transforming that of the low pass filter:()()⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛ω-ωωω+ω=4.66279.10690s )9.10690)(4.6627(s 5.2360H s s H )s (H 2L l u u l 2pL BP⎪⎪⎭⎫⎝⎛+=s 5.4063)9.10690)(4.6627(s 5.2360H 2L 7.70852870s 5.4063s s5.40635.2360s5.4063)9.10690)(4.6627(s 5.23605.236022++=++=The bilinear transformation gives the digital transfer function:7.708528701z 1z 160005.40631z 1z 160001z 1z 160005.4063)z (H 2BP +⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-=()212z6682.0z9449.01z 11659.0---+--=10.19 The lower pre-warped cut-off frequency is Ωl = =π20005520.055π rads , or ωl =4.3462055.0tan f 2S =π rad/sec. The upper pre-warped cut-off frequency is Ωu ==π20006520.065π rads , or ωu = 8.4092065.0tanf 2S =π rad/sec. A band stop filter maybe obtained from an arbitrary low pass filter, such as,5.2360s 5.2360s )s (H pp L +=ω+ω=Transforming the low pass transfer function into a band stop transfer function,()()()()⎪⎪⎭⎫⎝⎛+-=⎪⎪⎭⎫ ⎝⎛ωω+ω-ωω=8.4094.346s 4.3468.409s 5.2360H s s H )s (H 2L u l 2l up L BS ()()⎪⎪⎭⎫ ⎝⎛+=8.4094.346s s4.635.2360H 2L ()()7.141954s 4.63s 7.141954s 5.23608.4094.346s s4.635.23605.2360222+++=++=The transfer function for the digital filter is found using the bilinear transformation:7.1419541z 1z 40004.631z 1z 40007.1419541z 1z 4000)z (H 22BS +⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-=2121z9691.0z9344.11z9845.0z 9344.19845.0----+-+-=The frequency response of the filter isΩ-Ω-Ω-Ω-+-+-=Ω2j j 2j j BS e9691.0e9344.11e9845.0e 9344.19845.0)(HIt may be used to find the magnitude response for the filter, plotted below against frequency in Hz.10.20 The low pass prototype for the filter has a cut-off of 30 Hz, equal to the bandwidth of the filter. The transfer function for a second order low pass analog Butterworth filter is:21p 1p 221p s 2s )s (H ω+ω+ω=A low pass filter with a cut-off frequency of 30 Hz would giveΩp1 = π=π=π3.0200302f f 2S1p radians|Hωp1 = 8.2032tanf 21p S =Ω rad/secThis gives a low pass analog transfer function41209s 2.288s 41209)s (H 2++=This low pass filter with cut-off ωp = ωp1 = 203.8 rad/sec may be converted to a high pass filter with cut-off 'p ω using the conversion⎪⎪⎭⎫⎝⎛ωω=s H )s (H 'pp L HThe high pass cut-off, f S /2 – 30 = 100 – 30 = 70 Hz gives:'p Ω = π=π=π7.0200702f f 2Sl radians'p ω= 0.7852tanf 21p S =Ω rad/secThe conversion formula becomes⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛ωω=s 159983H s H )s (H L 'pp L HThe analog transfer function for the band pass filter is41209s 1599832.288s 159********)s (H 2+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=5.621091s 9.1118s s22++=The bilinear transformation1z 1z 4001z 1z f 2s S+-=+-=converts this transfer function to a digital transfer function:5.6210911z 1z 4009.11181z 1z 4001z 1z 400)z (H 22+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-=2121z2715.0z7506.01)zz 21(1302.0----+++-=10.21 (a)For a 1 kHz tone at a sampling rate of 4 kHz, the digital frequency isπ=π=π=Ω5.0400010002f f 2S. The z transform for a sine wave, and therefore also thetransfer function for a sine wave generator, is 2122z1z1z z 1cos z 2z sin z )z (H --+=+=+Ω-Ω=.(b)The frequency response for the filter is Ω-Ω-+=Ω2j j e1e)(H . The magnitude response,or filter shape, is plotted below.10.22 (a) Using t = nT, the sampled version of the impulse response is h[n] = nT 2e -With β = e –2T , the third row of Table 6.1 gives the transfer functionH(z) =1T2T2ze11ez z ----=-The filter shape can be obtained from the frequency response H(Ω) =Ω---j T2ee11(i) Ω---=Ωj 2ee11)(H (ii) Ω---=Ωj 1ee 11)(H(b)Analog frequencies in Hz are converted to analog frequencies in rad/sec throughω = 2πf, and to digital frequencies in rads through fT2f f 2Sπ=π=Ω. The figure belowshows the results. Note that the Nyquist frequency for T = 1 is 0.5 Hz, and the Nyquist frequency for T = 0.5 is 1 Hz. This explains the repetitive shapes in the figure. (c) Within Nyquist limits, the faster the sampling rate, the better the approximation to the analog filter, but even T = 0.5 is not sufficient. To follow the analog filter shape for the range shown in the figure, a sampling rate of more than 8 samples per second is needed, that is T < 1/8.10.23 The first order Butterworth transfer function H(s) for a 4 kHz cut-off frequency isπ+π=π+π=ω+ω=8000s 8000)4000(2s )4000(2s )s (H 1p 1pThe filter shape for this analog filter is180001)(H 2+⎪⎭⎫ ⎝⎛πω=ωThis shape is to be duplicated by a digital filter designed with the impulse invariancemethod. The transfer function of the digital filter is111p ze18000ze1)z (H T8000T1p --π-ω--π=-ω=The frequency response of the digital filter isΩ-π-Ω-ω--π=-ω=Ωj T8000j T1p ee18000ee1)(H 1pWith T = 1/f S = 1/32000, the digital filter shape becomesΩ-π-Ω-ω--π=-ω=Ωj 25.0j T1p ee18000ee1)(H 1pUsing the tricks described in the solution to question 10.22, the analog and digital filter shapes can be compared against frequency in Hz, as shown below.10.24 The digital impulse response h[n] obtained by sampling is:h[n] =()T n 300sin e3001nT200-u[n]From Table 6.1, the z transform of ]n [u )n sin(n Ωβ is22cos z 2z sin z β+Ωβ-Ωβ. WithT200e-=β and T 300=Ω, the transfer function for the digital filter becomesH(z) =()()T400T2002T200eT 300cos z e2z T 300sin z e3001---+-With a sampling interval of 2 msec, this transfer function becomesH(z) =()()2118.04.024.0z4493.0z1065.11z00126.0e6.0cos z e2z 6.0sin z e3001------+-=+-The filter shape |H(Ω)| may be found from the frequency responseΩ-Ω-Ω-+-=Ω2j j j e4493.0e1065.11e00126.0)(HFrequency (Hz)The filter shape is shown below. The same trick as was used in the last two solutions is used here to plot the analog and digital filter shapes on the same graph. The 2 msec sampling interval corresponds to a 500 Hz sampling rate, so the Nyquist limit for the digital filter is evident at 250 Hz. Note that the digital filter shape could also be obtained by taking the DTFT of some large number of samples of h[n].10.25 (a) Quantized to 4 bits, the transfer function becomes321321z0625.0z6875.0z0625.11z375.0z0625.1z0625.1375.0)z(H------++++++=(b) Quantized to 5 bits, the transfer function becomes321321z09375.0z6875.0z0625.11z34375.0z0625.1z0625.134375.0)z(H------++++++=The filter shape for the original filter and two quantized copies of it are shown below.。