向量的直角坐标运算教学设计
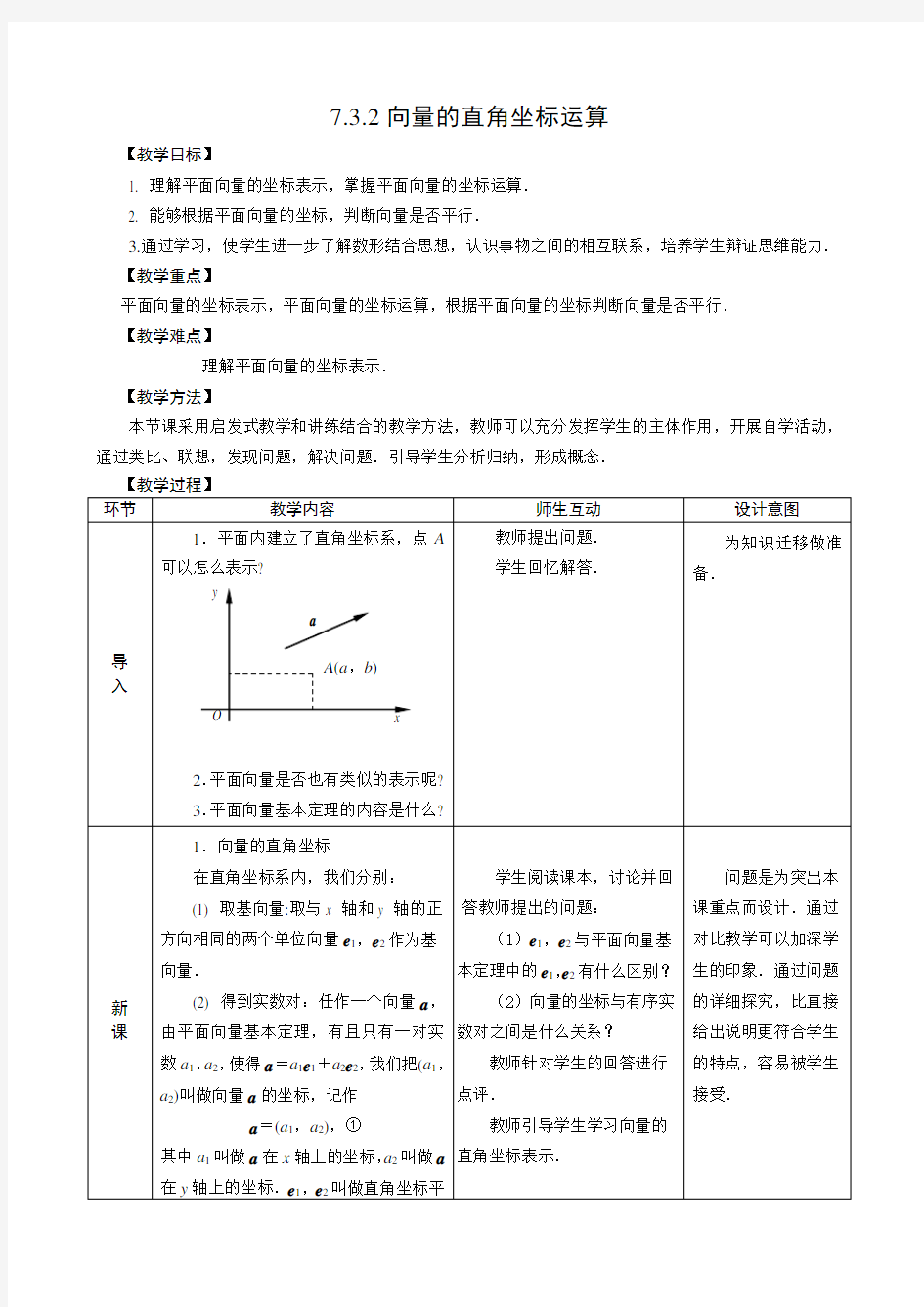

7.3.2向量的直角坐标运算
【教学目标】
1. 理解平面向量的坐标表示,掌握平面向量的坐标运算.
2. 能够根据平面向量的坐标,判断向量是否平行.
3.通过学习,使学生进一步了解数形结合思想,认识事物之间的相互联系,培养学生辩证思维能力.
【教学重点】
平面向量的坐标表示,平面向量的坐标运算,根据平面向量的坐标判断向量是否平行.
【教学难点】
理解平面向量的坐标表示.
【教学方法】
本节课采用启发式教学和讲练结合的教学方法,教师可以充分发挥学生的主体作用,开展自学活动,通过类比、联想,发现问题,解决问题.引导学生分析归纳,形成概念.
【教学过程】
高中数学-空间直角坐标系与空间向量典型例题
高中数学-空间直角坐标系与空间向量 一、建立空间直角坐标系的几种方法 构建原则: 遵循对称性,尽可能多的让点落在坐标轴上。 作法: 充分利用图形中的垂直关系或构造垂直关系来建立空间直角坐标系. 类型举例如下: (一)用共顶点的互相垂直的三条棱构建直角坐标系 例1 已知直四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,底面ABCD 是直角梯形,∠ A 为直角,A B ∥CD ,AB =4,AD =2,D C =1,求异面直线BC 1与DC 所成角的余弦 值. 解析:如图1,以D 为坐标原点,分别以DA 、DC 、DD 1所在直线为x 、y 、z 轴建立空间直角坐标系,则C 1(0,1,2)、B (2,4,0), ∴1(232)BC =--u u u u r ,,,(010)CD =-u u u r ,,. 设1BC u u u u r 与CD uuu r 所成的角为θ, 则11317 cos 17BC CD BC CD θ== u u u u r u u u r g u u u u r u u u r . (二)利用线面垂直关系构建直角坐标系 例2 如图2,在三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于 C 、C 1的一点,EA ⊥EB 1.已知2AB = ,BB 1=2,BC =1,∠BCC 1= 3 π .求二面角A -EB 1-A 1的平面角的正切值. 解析:如图2,以B 为原点,分别以BB 1、BA 所在直线为y 轴、z 轴,过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系. 由于BC =1,BB 1=2,AB = 2,∠BCC 1= 3 π,
空间向量的坐标运算练习
空间向量的坐标运算练 习 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
空间向量的坐标运算——1 1、已知向量b ,a 分别平行于x 、y 轴,则它们的坐标各有什么特点 答:a 的__________________________; b 的________________________________ 2、如果的横坐标为0,其它坐标都不为0,则与哪个坐标平面平行答:_________ 4、点P(2,-3,4)在xoy 面上的射影坐标是___________;在xoz 面上的射影坐标是 ___________; 在yoz 面上的射影坐标是___________ 5、点Q (-3,2,5)关于原点对称的点的坐 标是___________;关于xoz 面对称的点的坐标是__________________ 6、已知A (3,4,5),B (0,2,1),若 AB 5 2OC =,则C 点的坐标是______________ 7、写出与原点距离等于3的点所满足的条件________________________________ 8、已知A(2,0,0),B(6,2,2),C(4,0, 2) A :2 D 3C 4B 6ππππ ::: 9、如图,ABC-A 1B 1C 1是正三棱柱(即底面是正三角形,沿着垂直于底面的向量平移所得到的轨迹),若AB =2,AA 1=4,R 是BB 1的中点,取AB 的中点为原点建立坐标系如图,写出下列向量的坐标: ______________= ______________=______________=A A'
《空间向量运算的坐标表示》说课稿
《空间向量运算的坐标表示》——说课稿 各位评委、老师:大家好! 今天我说课的内容是《空间向量运算的坐标表示》的第一课时,我将从教材分析、教学目标、学生情况、教法学法分析、教学过程、教学效果及反思六个方面来介绍: 一、教材分析 (一)地位和作用 本节课内容选自人教数学选修2-1第三章,这节课是在学生学习了空间向量几何形式及其运算、空间向量基本定理的基础上进一步学习的知识内容,是在学生已经学过的二维的平面直角坐标系的基础上的推广,是《空间向量运算的坐标表示》的第一课时,是以后学习“立体几何中的向量方法”等内容的基础。它将数与形紧密地结合起来。这节课学完后,如把几何体放入空间直角坐标系中来研究,几何体上的点就有了坐标表示,一些题目如两点间距离、异面直线成的角等就可借助于空间向量来解答,所以,这节课对于沟通高中各部分知识,完善学生的认知结构,起到了很重要的作用。 (二)目标的确定及分析 根据新课标和我对教材的理解,结合学生实际水平,从知识与技能;过程和方法;情感态度价值观三个层面出发,我将本课的目标定位以下三个:(1)知识与技能:通过与平面向量类比学习并掌握空间向量加法、减法、数乘、数量积运算的坐标表示以及向量的长度、夹角公式的坐标表示,并能初步应用这些知识解决简单的立体几何问题。(2)过程与方法:①通过将空间向量运算与熟悉的平面向量的运算进行类比,使学生掌握空间向量运算的坐标表示,渗透类比的数学方法;②会用空间向量运算的坐标表示解决简单的立体几何问题,体会向量方法在研究空间图形中的作用,培养学生的空间想象能力和几何直观能力。(3)情感态度价值观:通过提问、讨论、合作、探究等主动参与教学的活动,培养学生主人翁意识、集体主义精神。 (三)重难点的确定及分析 本节课的重点是:空间向量运算的坐标表示,应用向量法求两条异面直线所
空间向量的坐标运算(人教A版)(含答案)
空间向量的坐标运算(人教A版) 一、单选题(共10道,每道10分) 1.已知点的坐标分别为与,则向量的相反向量的坐标是( ) A. B. C. D. 答案:A 解题思路: 试题难度:三颗星知识点:空间向量运算的坐标表示 2.已知空间直角坐标系中且,则点的坐标为( ) A. B. C. D. 答案:A 解题思路:
试题难度:三颗星知识点:空间向量运算的坐标表示 3.若向量,,则向量的坐标是( ) A. B. C. D. 答案:D 解题思路: 试题难度:三颗星知识点:空间向量运算的坐标表示 4.已知向量,,则=( ) A. B. C. D. 答案:C
解题思路: 试题难度:三颗星知识点:空间向量运算的坐标表示 5.已知向量是空间的一组单位正交基底,若向量在基底下的坐标为,那么向量在基底下的坐标为( ) A. B. C. D. 答案:C 解题思路: 试题难度:三颗星知识点:空间向量的基本定理及其意义 6.已知为空间的一组单位正交基底,而是空间的另一组
基底,若向量在基底下的坐标为,则向量在基底下的坐标为( ) A. B. C. D. 答案:A 解题思路: 试题难度:三颗星知识点:空间向量的基本定理及其意义 7.已知三点不共线,点为平面外的一点,则下列条件中,能使得平面成立的是( ) A. B. C. D. 答案:B 解题思路:
试题难度:三颗星知识点:共线向量与共面向量 8.已知,,,若,,三向量共面,则实数=( ) A. B.
C. D. 答案:D 解题思路: 试题难度:三颗星知识点:共线向量与共面向量 9.已知空间三点的坐标为,,,若三点共线,则=( ) A. B. C. D. 答案:D 解题思路:
空间向量的基本运算
第六节 空间向量 1. 空间向量的概念:在空间,我们把具有 和 的量叫做向量。 2. 空间向量的运算。 定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。 OB OA AB a b =+=+;BA OA OB a b =-=-;()OP a R λλ=∈ 运算律:⑴加法交换律:a b b a +=+ ⑵加法结合律:)()(c b a c b a ++=++ ⑶数乘分配律:b a b a λλλ+=+)( 3. 共线向量。 (1)如果表示空间向量的有向线段所在的直线 或 ,那么这些向量也叫做共 线向量或平行向量,a 平行于b ,记作b a //。 (2)共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 存在实数λ, 使a = 。 4. 共面向量 (1)定义:一般地,能平移到同一 内的向量叫做共面向量。 说明:空间任意的两向量都是 的。 (2)共面向量定理:如果两个向量,a b 不共线,p 与向量,a b 共面的条件是存在实数,x y ,使 。 5. 空间向量基本定理:如果三个向量,,a b c 不共面,那么对空间任一向量p ,存在一个唯一的有序实数组,,x y z ,使 。 若三向量,,a b c 不共面,我们把{,,}a b c 叫做空间的一个基底,,,a b c 叫做基向量,空间任意三个 的向量都可以构成空间的一个基底。 推论:设,,,O A B C 是不共面的四点,则对空间任一点P ,都存在唯一的三个有序实数,,x y z ,使OP xOA yOB zOC =++。 6. 空间向量的直角坐标系: (1)空间直角坐标系中的坐标: 在空间直角坐标系O xyz -中,对空间任一点A ,存在唯一的有序实数组(,,)x y z ,使zk yi xi OA ++=,有序实数组 (,,)x y z 叫作向量A 在空间直角坐标系O xyz -中的坐标,记作
空间向量的坐标运算
空间向量的坐标运算 第一课时空间直角坐标系 教学目标: ㈠知识目标: ⒈空间直角坐标系; ⒉空间向量的坐标表示; ⒊空间向量的坐标运算; ⒋平行向量、垂直向量坐标之间的关系; 5.中点公式。 ㈡能力目标: ⒈掌握空间右手直角坐标系的概念,会确定一些简单几何体(正方体、长方体)的顶点坐标; ⒉掌握空间向量坐标运算的规律; 3.会根据向量的坐标,判断两个向量共线或垂直; 4.会用中点坐标公式解决有关问题。 教学重点:空间右手直角坐标系,向量的坐标运算 教学难点:向量坐标的确定 教学方法:讨论法. 教具准备:多媒体投影. 教学过程: 复习回顾 空间向量基本定理 探索研究 1、空间右手直角坐标系的概念 ⑴单位正交基底如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用{i,j,k}表示。 ⑵空间直角坐标系O-xyz 在空间选定一点O和一个单位正交基底{i,j,k},以点O 为原点,分别以i、j、k的方向为正方向建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们说建立了一个直角坐标系O-xyz,点O叫做原点,向量i,j,k叫做坐标向 量,通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面,yOz平面,zOx平面。 ⑶空间直角坐标系的画法作空间直角坐标系O-xyz 时,一般使∠xOy=135°(或45°),∠yOz=90°。 注:在空间直角坐标系O-xyz中,让右手拇指指向x轴 的正方向,食指指向y轴的正方向,如果中指能指向z轴的正 方向,则称这个坐标系为右手直角坐标系。 ⑷空间向量的坐标表示给定一空间直角坐标系和向
向量的直角坐标运算设a=(a 1,a 2,a 3),b=(b 1,b 2,b 3),则a+b=(a 1+b 1,a 2+b 2,a 3+b 3) a -b=(a 1- b 1,a 2-b 2,a 3-b 3)λa=(λa 1,λa 2,λa 3) a ?b=a 1 b 1+a 2b 2+a 2b 2 a//b a 1=λb 1,a 2=λb 2,a 3=λb 3(λ∈R)a ⊥b a 1b 1+a 2b 2+a 3b 3=0设A(x 1,y 1,z 1),B(x 2,y 2,z 2),则 AB =OB -OA =(x 2-x 1,y 2-y 1,z 2-z 1) 量a ,且设i,j,k 为坐标向量(如图),由空间向量基本定理,存在唯一的有序实数组(a 1,a 2,a 3)叫做向量a 在此直角坐标系中的坐标,可简记作a =(a 1,a 2,a 3)。 在空间直角坐标系O -xyz 中,对于空间任一点A ,对应一个向量OA ,若 ,k z j y i x OA ++=则有序数组(x,y,z)叫做点A 在 此空间直角坐标系中的坐标,记为A(x,y,z),其中x 叫做A 的横坐标,y 叫做点A 的纵坐标,z 叫做点A 的竖坐标,写点的坐标时,三个坐标间的顺序不能变。 ⑸空间任一点P 的坐标的确定 过P 分别作三个与坐标平面平行的平面(或垂面),分别交坐标轴于A 、B 、C 三点,|x|=|OA|,|y|=|OB|,|z|=|OC|,当OA 与i 方向相同时,x >0,反之x <0,同理可确定y 、z (如图) 例1已知ABCD -A 1B 1C 1D 1是棱长为2的正方体,E 、F 分别是BB 1和DC 的中点,建立如图所示的空间直角坐标系,试写出图中各点的坐标。 分析:要求点E 的坐标,过点E 与x 轴、y 轴垂直的平面已存在,只要过E 作平面垂直于z 轴交E ‘ 点,此时|x|=|,|DA |y|=|,|DC |z|=||'DE ,当DA 的方向与x 轴正向相同时,x >0,反之x <0,同理确定y 、z 的符号,这样可求得点E 的坐标。 解:D(0,0,0),A(2,0,0),B(0,2,0),C(0,0,2), A 1(2,0,2), B 1(2,2,2), C 1(0,2,2),, D 1(0,0,2),E(2,2,1),F(0,1,0) 2、向量的直角坐标运算 注:3 32 21 1i 321321b a b a b a b //a 1,2,3),0(i b ),b ,b ,(b b ),a ,a ,(a a = = ? =≠==则若
高考试题分类考点空间直角坐标系空间向量及其运算
高考试题分类考点空间直角坐标系空间向量及其运算
————————————————————————————————作者:————————————————————————————————日期:
考点37 空间直角坐标系、空间向量及其运算 一、解答题 1.(2012·北京高考理科·T16)如图1,在Rt △ABC 中,∠C=90°,BC=3,AC=6,D ,E 分别是AC ,AB 上的点,且DE ∥BC ,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD,如图 2. (1) 求证:A 1C ⊥平面BCDE ; (2) 若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小; (3) 线段BC 上是否存在点P ,使平面A 1DP 与平面A 1BE 垂直?说明理由. 【解题指南】(1)利用线面垂直的判定定理证明;(2)(3)找出三个垂直关系, 建系,利用向量法求解. 【解析】(1)//,,DE BC AC BC DE AC ⊥∴⊥Q ,1,DE A D DE CD ∴⊥⊥, 111 ,,A D CD D DE ACD DE AC =∴⊥∴⊥Q I 面 又11,,AC CD CD DE D AC BCDE ⊥=∴⊥Q I 面. (2)由(1)可知,1,,CB CD AC 两两互相垂直,分别以它们为x 轴、y 轴、z 轴 建立空间直角坐标系,则1(0,0,23)A ,(0,1,3),(0,1,3),(1,2,0),M CM BE ==-u u u u r u u u r 1(3,0,23)A B =-u u u r ,设平面1A BE 的法向量为1111(,,)n x y z =u r , 由 1111111203230n BE x y n A B x z ??=-+=???=-=??u r u u u r u r u u u r ,令11x =,得113(1,,)22 n =u r , A B C D E C B E D A M 图图
空间向量及其运算练习题
空间向量及其运算练习题 一、选择题 1、在空间直角坐标系中,已知点P (x ,y ,z ),下列叙述中正确的个数是 ①点P 关于x 轴对称点的坐标是P 1(x ,-y ,z ) ②点P 关于yOz 平面对称点的坐标是P 2(x ,-y ,-z ) ③点P 关于y 轴对称点的坐标是P 3(x ,-y ,z ) ④点P 关于原点对称的点的坐标是P 4(-x ,-y ,-z ) A.0 B.1 C.2 D.3 2、点(2,3,4)关于xoz 平面的对称点为( ) A 、(2,3,-4) B 、(-2,3,4) C 、(2,-3,4) D 、(-2,-3,4) 3、在空间直角坐标系中,设z 为任意实数,相应的点(3,1,)P z 的集合确定的图形为 ( )A .点 B .直线 C .圆 D .平面 4、在平行六面体ABCD —A 1B 1C 1D 1中,M 为AC 与BD 的交点,若B A 1=a ,11D A =b , A A 1=c .则下列向量中与M B 1相等的向量是( ) A .c b a ++- 21 21 B . c b a ++21 21 C .c b a +-2 1 21 D .c b a +--2 1 21 5、在下列条件中,使M 与A 、B 、C 一定共面的是 ( ) A .OC O B OA OM --=2 B .O C OB OA OM 2 1 3151++= C .=++MC MB MA 0 D .=+++OC OB OA OM 0 5、已知平行六面体''' ' ABCD A B C D -中,AB=4,AD=3,' 5AA =,0 90BAD ∠=, ''060BAA DAA ∠=∠=,则'AC 等于 ( ) A .85 B .85 C .52 D .50 图
最新空间向量运算的坐标表示练习题
课时作业(十七) [学业水平层次] 一、选择题 1.已知a =(1,-2,1),a -b =(-1,2,-1),则b =( ) A .(2,-4,2) B .(-2,4,-2) C .(-2,0,-2) D .(2,1,-3) 【解析】 b =a -(-1,2,-1)=(1,-2,1)-(-1,2,-1)=(2,-4,2). 【答案】 A 2.设A (3,3,1),B (1,0,5),C (0,1,0),则AB 的中点M 到点C 的距离|CM |的值为( ) A.534 B.532 C.532 D.132 【解析】 ∵AB 的中点M ? ? ???2,32,3,∴CM →=? ????2,12,3,故|CM | =|CM → |= 22+? ?? ??122+32=532. 【答案】 C 3.(2014·德州高二检测)已知向量a =(2,3),b =(k,1),若a +2b 与a -b 平行,则k 的值是( ) A .-6 B .-23 C.2 3 D .14 【解析】 由题意得a +2b =(2+2k,5),且a -b =(2-k,2),又因为a +2b 和a -b 平行,则2(2+2k )-5(2-k )=0,解得k =2 3.
【答案】 C 4. (2014·河南省开封高中月考)如图3-1-32,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=2,E ,F 分别是面A 1B 1C 1D 1、面BCC 1B 1的中心,则E ,F 两点间的距离为( ) 图3-1-32 A .1 B.52 C.62 D.32 【解析】 以点A 为原点,建立如图所示的空间直角坐标系,则 E (1,1,2), F ? ???? 2,1,22,所以|EF |= (1-2)2 +(1-1)2 +? ??? ?2-222 =6 2,故选C. 【答案】 C 二、填空题 5.(2014·青岛高二检测)已知点A (1,2,3),B (2,1,2),P (1,1,2),O (0,0,0),点Q 在直线OP 上运动,当QA →·QB →取得最小值时,点Q 的坐标为________. 【解析】 设OQ →=λOP →=(λ,λ,2λ),故Q (λ,λ,2λ),故QA → =
3.1.4空间向量的直角坐标运算 自制 2014年
3.1.4空间向量的直角坐标运算(课前预习案) 班级:___ 姓名:______ 一、新知导学 1、空间向量的直角坐标运算律: (1)若123(,,)a a a a =,(,,)123b b b b =,则 a b += , a b -= , a λ= , a b ?= , //a b ? a b ⊥? . (2)若(,,)111A x y z ,222(,,)B x y z ,则AB = . 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的______的坐标减去_________的坐标 2、模长公式: 若123(,,)a a a a =,123(,,)b b b b =, 则||a a a = ?= ,||b b b =?= . 3、夹角公式:2cos ||||a b a b a b a ??== ?+ 4、两点间的距离公式: 若111(,,)A x y z ,222(,,)B x y z ,则2 ||(AB AB x ==, 或,A B d =
;,,i j k ??,求下列向量的坐标:)346a i j k =+- ()2 323 b i j k =--+ 若(2,1,3),(5,3,2)a b =-=-,则a +b =____________,32a b -=___________, a b ?=_____,(2)(3)a b a b +?-=______________1)(0,0,4),(0,0,7) (2)((3,4,0),(0,0,6) (2)(-2,1,,-5,7) 已知(1,1,1),(1,0,1)a b =--=-,则______,a =,a b <>=____________3.1.4 空间向量的直角坐标运算(课堂探究案)一、空间向量的直角坐标 向量(,,a a a a =二、向量的坐标运算 已知(1,1,0),(0,1,1),(1,0,1)a b c ===,,2p a b q a b c =-=+-,求: ,p q ,p q ?。
空间向量的直角坐标及其运算
课 题:9 6 空间向量的直角坐标及其运算 (一) 教学目的: ⒈掌握空间右手直角坐标系的概念,会确定一些简单几何体(正方体、长方体)的顶点坐标; ⒉掌握空间向量坐标运算的规律; 3.会根据向量的坐标,判断两个向量共线或垂直; 4.会用中点坐标公式解决有关问题 教学重点:空间右手直角坐标系,向量的坐标运算 教学难点:空间向量的坐标的确定及运算 内容分析: 本节有两个知识点:向量和点的直角坐标及向量的坐标运算、夹角和距离公式这一小节,我们在直角坐标系下,使向量运算完全坐标化去掉基底,使空间一个向量对应一个三维数组,这样使向量运算更加方便在上一小节已学习向量运算的基础上,把向量运算完全坐标化,对学生已不会感到抽象和困难在第2个知识点中,我们给出空间解析几何两个最基本的公式:夹角和距离公式在这个知识点中,作为向量坐标计算的例题,还顺便证明了直线与平面垂直的“性质定理”通过解一些立体几何的应用题,就可为学生今后进一步学习空间解析几何、高维向量和矩阵打下基础 要求学生理解空间向量坐标的概念,掌握空间向量的坐标运算,掌握两点的距离公式垂直于平面的性质定理 教学过程: 一、复习引入: 平面向量的坐标表示 分别取与x 轴、y 轴方向相同的两个单位向量i 、j 作为基底任作一个向量a ,由平面向量基本 定理知,有且只有一对实数x 、y ,使得j y i x a += 把),(y x 叫做向量a 的(直角)坐标,记作),(y x a = 其中x 叫做a 在x 轴上的坐标,y 叫做a 在y 轴上的坐 标, 特别地,)0,1(=i ,)1,0(=j ,0,0(0= 2.平面向量的坐标运算 若),(11y x a = ,),(22y x b = , 则b a +),(2121y y x x ++=,b a -),(2121y y x x --=,,(y x a λλλ= 若),(11y x A ,),(22y x B ,则()1212,y y x x --= 3.a ∥b (b ≠0)的充要条件是x 1y 2-x 2y 1=0 4平面两向量数量积的坐标表示 已知两个非零向量),(11y x a = ,),(22y x b = ,试用a 和b 的坐标表示b a ? 设i 是x 轴上的单位向量,j 是y 轴上的单位向量,那么 j y i x a 11+=,j y i x b 22+= 所以))((2211j y i x j y i x b a ++=?2211221221j y y j i y x j i y x i x x +?+?+= 又1=?i i ,1=?j j ,0=?=?i j j i 所以b a ?2121y y x x += 这就是说:两个向量的数量积等于它们对应坐标的乘积的和 5.平面内两点间的距离公式 (1)设),(y x a = ,则222||y x a += 或||a = (2)如果表示向量a 的有向线段的起点和终点的坐标分别为),(11y x 、),(22y x ,那么 221221)()(||y y x x a -+-= (平面内两点间的距离公式) 6.向量垂直的判定 设),(11y x a = ,),(22y x b = ,则b a ⊥ ?02121=+y y x x 7.两向量夹角的余弦(πθ≤≤0) cos <a ,b >= co s θ=||||b a b a ?? 8.空间向量的基本定理:若{,,}a b c 是空间的一个基底,p 是空间任意一向量,存在唯一的实数 组,,x y z 使p xa yb zc =++ . 二、讲解新课: 1 空间直角坐标系: (1)若空间的一个基底的三个基向量互相垂直,且长为1, 这个基底叫单位正交基底,用{,,}i j k 表示;
空间向量运算的坐标公式
空间向量运算的坐标公式 如果三个向量不共面那么对空间任一向量存在一个唯一的 有序实数组x、y、z使得cbapczbyaxpcba叫做空间的一个 ______基底空间任意三个不共面向量都可以构成空间的一 个基底一、空间直角坐标系单位正交基底如果空间的一个基底的三个基向量互相垂直且长都为1则这个基底叫做单位正交基底常用i j k 来表示.点O叫做原点向量i、j、k都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面。分别称为xOy平面yOz平面xOz平面.空间直角坐标系在空间选定一 点O和一个单位正交基底i、j、k 。以点O为原点分别以i、j、k的正方向建立三条数轴x轴、y轴、z轴它们都叫做坐 标轴.这样就建立了一个空间直角坐标系O--xyzOxyzijk二、 向量的直角坐标aaaa 1 2 3给定一个空间坐标系和向量且设i、j、k为坐标向量由空间向量基本定理存在唯一的有序实数组1 2 3使1i 2j 3k 有序数组1 2 3叫做在空间直角坐标系 O--xyz中的坐标记作.aaaaaaaaaaaaxyzOAa1a2a3ijka在空间直角坐标系O--xyz中对空间任一点A对应一个向量OA于是 存在唯一的有序实数组xyz使OAxiyjzk在单位正交基底i j k 中与向量OA对应的有序实数组xyz叫做点A在此空间直角坐标系中的坐标记作Axyz其中x叫做点A的横坐标y叫做点A的纵坐标z叫做点A的竖坐标.xyzOAxyzijka三、向量 的直角坐标运算.111222axyzbxyz设则 121212abxxyyzz111axyzR121212abxxyyzz121212abxxyyzz例
空间向量及其运算的坐标表示
1.3 空间向量及其运算的坐标表示 【学习目标】 1.空间直角坐标系 在空间选定一点O和一个单位正交基底{i,j,k},以O为原点,分别以i,j,k方向为正方向,以它们的长为单位长度建立三条数轴:x轴,y轴,z轴,它们都叫做坐标轴,这时我们就建立,O叫做,i,j,k都叫做。 对于空间任意一个向量p,存在有序实数组{x,y,z},使得p=x e1+y e2+z e3,则把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作。 2.空间向量的坐标运算 空间向量a,b,其坐标形式为a=(a1,a2,a3),b=(b1,b2,b3). 3. 设a=(a1,a2,a3),b=(b1,b2,b3),则
夹角 cos 〈a ,b 〉=a ·b |a ||b | cos 〈a ,b 〉= a 1 b 1+a 2b 2+a 3b 3 a 21+a 22+a 2 3 b 21+b 22+b 2 3 1.已知i ,j ,k 分别是空间直角坐标系Oxyz 中x 轴,y 轴,z 轴的正方向上的单位向量,且AB → =-i +j -k ,则点B 的坐标是( ) A .(-1,1,-1) B .(-i ,j ,-k ) C .(1,-1,-1) D .不确定 2、判断对错。 (1)空间直角坐标系中,向量AB → 的坐标与终点B 的坐标相同.( ) (2)设a =(x 1,y 1,z 1),b =(x 2,y 2,z 2)且b ≠0,则a ∥b ∥x 1x 2 =y 1y 2 =z 1 z 2 .( ) (3)四边形ABCD 是平行四边形,则向量AB →与DC → 的坐标相同.( ) (4)设A (0,1,-1),O 为坐标原点,则OA → =(0,1,-1).( ) 【经典例题】 题型一 空间直角坐标系 注意:建系时要充分利用图形的线面垂直关系,选择合适的基底,在写向量的坐标时,考虑图形的性质,充分利用向量的线性运算,将向量用基底表示. 例1已知P A 垂直于正方形ABCD 所在的平面,M 、N 分别是AB 、PC 的中点,并且P A =AD =1,建立适当坐标系,求向量MN → 的坐标.
空间向量及其坐标运算练习题
空间向量及其坐标运算 一.选择题 1.若a =(2x ,1,3),b =(1,-2y ,9),如果a 与b 为共线向量,则 A.x =1,y =1 B.x = 21,y =-21 C.x =61,y =-23 D.x =-61,y =2 3 2.在空间直角坐标系中,已知点P (x ,y ,z ),下列叙述中正确的个数是 ①点P 关于x 轴对称点的坐标是P 1(x ,-y ,z ) ②点P 关于yOz 平面对称点的坐标是P 2(x ,-y ,-z ) ③点P 关于y 轴对称点的坐标是P 3(x ,-y ,z ) ④点P 关于原点对称的点的坐标是P 4(-x ,-y ,-z ) A.0 B.1 C.2 D.3 3.已知向量a =(1,1,0),b =(-1,0,2),且k a +b 与2a -b 互相垂直,则k 值是 A.1 B.51 C.53 D.5 7 4.设OABC 是四面体,G 1是△ABC 的重心,G 是OG 1上一点,且OG =3GG 1,若OG = x OA +y OB +z OC ,则(x ,y ,z )为 A.( 41,41,41) B.(43,43,43) C.(31,31,31) D.(32,32,32 ) 5.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成的角为的余弦值 A D B C B C D 1 1 1 1 M N A. 2 3 B. 10 10 C. 5 3 D. 5 2 二.填空题 6.已知空间三点A (1,1,1)、B (-1,0,4)、C (2,-2,3),则AB 与CA 的夹角 θ的大小是_________. 7.已知点A (1,2,1)、B (-1,3,4)、D (1,1,1),若AP =2PB ,则|PD |的值是__________. 8.命题:①若a 与b 共线,b 与c 共线,则a 与c 共线;②向量a 、b 、c 共面,则它们所在的直线也共面;③若a 与b 共线,则存在唯一的实数λ,使b =λa ;④若A 、B 、C 三点不共线,O 是平面ABC 外一点,OM = 31OA + 31OB + 3 1 OC ,则点M 一定在平面ABC 上,且在△ABC 内部. 上述命题中的真命题是_____________.
空间向量的坐标表示及其运算
空间向量的坐标表示及其运算 1. 已知()2,1,3=,()3,2,1-B ,则A 的坐标是 . 2. 已知()()m b a ,4,2,2,2,1-=-= ,若b a //,则实数=m . 3. 在空间直角坐标系中,已知点A (1,0,2),B(1,-3,1),点M 在y 轴上,且M 到A 与到B 的距离相等,则M 的坐标是______ . 4. 若()1,1,1A ,()4,0,1-B ,()3,2,2-C ,则以AC AB ,为邻边的平行四边形的面积为 . 5. 若A(3cos α,3sin α,1),B(2cos α,2sin α,1),则|AB → |的取值范围是 . 6. 若()()222111,,,,,z y x A z y x A ,且P 为AB 中点,则P 的坐标为 . 7. 在长方体1111D C B A ABCD -中,3,4,51===AA BC AB ,如图,建立空间直角坐标系,写 出11,,CB B A AC 及D B 1. 8. 已知()()1,2,3,3,6,4--B A ,且3 2 -=,求点P 的坐标。 9. 已知()()5,3,2,1,5,1-==b a , (1)当()() b a b a 3//-+λ,求实数λ的值; (2)当()() b a b a 3/-⊥+λ,求实数λ的值 y
10. 已知空间三点()2,0,2-A ,()()4,0,3,2,1,1--C B ,求: (1)BAC ∠; (2)若向量k k +与向量k 2-垂直,求实数k 值。 11. 已知()3,2,1=,()2,1,2=,()2,1,1=,点S 在直线OP 上,求?的最小值,并指出此时S 的坐标。 12. 在棱长为a 的正四面体ABCD 中,建立恰当的坐标系, (1)求D C B A ,,,的坐标; (2)求AB BC ? +AC BD ? 的值。 C P A
空间向量的直角坐标运算
高二数学《空间向量的直角坐标运算》学案 学习目标: 1.掌握空间向量的坐标运算,会判定两个向量平行或垂直。 2.掌握模长公式,夹角公式,两点间距离公式,并会用这些公式解决有关问题。 学习重点: 向量的坐标运算,夹角和距离的求法以及平行,垂直的条件。 学习难点: 向量坐标的确定及公式的应用。 课题:空间向量的直角坐标运算(预习学案) 预习新知识 1.坐标运算: (1)建立空间直角坐标系O xyz -,分别沿x 轴,y 轴,z 轴的正方向引单位向量,,i j k , 则{,,}i j k 叫做 ,单位向量,,i j k 都叫做 . (2)在空间直角坐标系中,对空间任一点A ,存在唯一的有序实数组(,,)x y z ,使 O A x i y j z k =+ + ,有序实数组 叫作向量在空间直角坐标系O xyz -中的坐 标,记作 . (3)若123(,,)a a a a = ,123(,,)b b b b = ,则 _________________a b += ,_________________a b -= , __________________a λ= ,___________________a b ?= 。 2.平行垂直的条件 (1) //________________________a b ? , (2) ________________________a b ⊥? . 3.向量夹角与长度的坐标计算公式 (1)若123(,,)a a a a = ,123(,,)b b b b = , 则||______________a = = ,||________________b = = , cos ______________________|||| a b a b a b ??==? . 若111(,,)A x y z ,222(,,)B x y z 则 __________________AB = ,||___________________________AB = = .
空间向量的直角坐标运算
空间向量的直角坐标运算 一、目标与策略 明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数! 学习目标: ● 掌握空间向量的坐标表示、坐标运算、夹角公式、距离公式。 ● 能通过坐标运算判断向量的共线与垂直。 ● 理解直线的方向向量与平面的法向量,会求平面的法向量。 重点难点: ● 重点:掌握空间向量的坐标运算,能通过坐标运算判断向量的共线与垂直。 ● 难点:向量坐标的确定以及夹角公式,距离公式的应用。 学习策略: ● 空间向量的直角坐标运算和平面向量的直角坐标运算类似,两个向量的加、减、数乘运算就是向量的横坐标、纵坐标、竖坐标分别进行加、减、数乘运算;空间两个向量的数量积等于它们对应坐标的乘积之和。 ● 对于垂直问题,一般是利用0a b a b ⊥?=进行证明;对于平行问题,一般是利用共线向量和共面向量定理进行证明。 二、学习与应用 空间向量的基本定理 (一)共线向量定理: 空间任意两个向量a 、b (b ≠0),a //b 的充要条件是 (二)共面向量定理(平面向量的基本定理): 两个向量a 、b 不共线,向量p 与向量a 、b 共面的充要条件是 *推论:P 、A 、B 、C 四点共面的充要条件:对空间任意一点O ,有OP = (三)空间向量基本定理: 如果三个向量,,a b c 不共面,那么对空间任一向量p ,存在 的有序实数组{,,}x y z ,使p = 。 “凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对 知识回顾——复习 学习新知识之前,看看你的知识贮备过关了吗? 详细内容请参看网校资源ID :#tbjx7#281331
空间直角坐标系、空间向量及其运算专题
空间直角坐标系、空间向量及其运算专题 [基础训练组] 1.O 为空间任意一点,若OP →=34OA →+18OB →+18OC → ,则A ,B ,C ,P 四点( ) A .一定不共面 B .一定共面 C .不一定共面 D .无法判断
2.在空间四边形ABCD 中,AB →·CD →+AC →·DB →+AD →·BC → =( ) A .-1 B .0 C .1 D .不确定 3.如图所示,PD 垂直于正方形ABCD 所在平面,AB =2,E 为PB 的中点,cos 〈DP →,AE → 〉= 3 3 ,若以DA ,DC ,DP 所在直线分别为x ,y ,z 轴建立空间直角坐标系,则点E 的坐标为( ) A .(1,1,1) B.? ????1,1,12 C.? ????1,1,32 D .(1,1,2) 4.在△ABC 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF → =( ) A.89 B.109 C.259 D.269 5.如图所示,已知空间四边形OABC ,OB =OC ,且∠AOB =∠AOC =π3 ,则cos 〈OA →,BC → 〉
的值为( ) A .0 B.12 C.32 D.22 6.在四面体O -ABC 中,OA →=a ,OB →=b ,OC →=c ,D 为BC 的中点,E 为AD 的中点,则OE → = ________ .(用a ,b ,c 表示). 7.若向量a =(1,λ,2),b =(2,-1,2)且a 与b 的夹角的余弦值为8 9,则λ= ________ . 8.如图所示,已知二面角α—l —β的平面角为θ? ?? ?? θ∈? ????0, π2,AB ⊥BC ,BC ⊥CD ,AB 在平面β内,BC 在l 上,CD 在平面α内,若AB =BC =CD =1,则AD 的长为 ________ . 9.如图,四棱柱ABCD -A 1B 1C 1D 1的各个面都是平行四边形,E 、F 分别在B 1B 和D 1D 上,且BE =13BB 1, DF =2 3 DD 1.
空间向量直角坐运算
空间向量的直角坐标运算 目标认知 学习目标: 1.掌握空间向量的坐标表示、坐标运算、夹角公式、距离公式。 2.能通过坐标运算判断向量的共线与垂直. 3.理解直线的方向向量与平面的法向量.会求平面的法向量 重点: 掌握空间向量的坐标运算,能通过坐标运算判断向量的共线与垂直. 难点: 向量坐标的确定以及夹角公式,距离公式的应用 学习策略: ①空间向量的直角坐标运算和平面向量的直角坐标运算类似,两个向量的加、减、数乘运算就是向量的 横坐标、纵坐标、竖坐标分别进行加、减、数乘运算;空间两个向量的数量积等于它们对应坐标的乘 积之和。 ②对于垂直问题,一般是利用进行证明;对于平行问题,一般是利用共线向量和共面 向量定理进行证明. 知识要点梳理 知识点一:空间向量的基本定理 1.共线向量定理: 空间任意两个向量、(≠),//的充要条件是存在实数λ,使=λ 2.共面向量定理(平面向量的基本定理) 两个向量、不共线,向量与向量、共面的充要条件是存在唯一实数对,使. *推论:P、A、B、C四点共面的充要条件:,其中O为空间任意一点,x、y、z为实数,且x+y+z=1. 3.空间向量基本定理 如果三个向量不共面,那么对空间任一向量,存在唯一的有序实数组,使。 若三个向量、、不共面,我们把叫做空间的一个基底,叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。 知识点二:空间直角坐标系及空间向量的坐标表示 (1)单位正交基底 若空间的一个基底的三个基向量互相垂直,且长为,这个基底叫单位正交基底,常用表示; (2)空间直角坐标 在空间选定一点和一个单位正交基底,以点为原点,分别以的方向为正方向建立三条数轴: 轴、轴、轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系,点叫原点,向量都叫坐标向量。 通过每两个坐标轴的平面叫坐标平面,分别称为平面,平面,平面;
知识讲解_空间向量的直角坐标运算
空间向量的直角坐标运算 编稿:张林娟审稿:孙永钊 【学习目标】 1. 理解空间向量的基本定理,掌握空间向量的正交分解及其坐标表示; 2. 掌握空间向量的坐标运算、夹角公式、距离公式; 3. 能通过坐标运算判断向量的共线与垂直. 【要点梳理】 要点一:空间向量基本定理 1.空间向量基本定理 空间向量基本定理:如果123e e e ,,是空间三个不共面的向量,a 是空间任一向量,那么存在唯一一组实数123λλλ,,,使得 112233=++λλλa e e e . 特别地,当123e e e ,,两两垂直时,就能得到这个向量的一个正交分解. 2.基底、基向量概念 由空间向量的基本定理知,若三个向量123e e e ,,不共面,那么所有空间向量所组成的集合就是{a |112233=++λλλa e e e ,123λλλ,,∈R },这个集合可看做是由向量123e e e ,,生成的,所以我们把{123e e e ,,}称为空间的一个基底.123e e e ,,叫做基向量,空间任意三个不共面的向量都可构成空间的一个基底. 要点诠释: (1)空间任意三个不共面的向量都可以作为空间向量的一个基底; (2)由于零向量可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是零向量0; (3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念. 要点二:空间向量的坐标表示 1.单位正交基底 若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位正交基底,常用{,,}i j k 表示; 2.空间直角坐标系 在空间选定一点O 和一个单位正交基底()i j k ,,,以点O 为原点,分别以i j k ,,的方向为正方向建立三条数轴:x 轴、y 轴、z 轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系O xyz ,点O 叫原点,向量i j k ,,都叫坐标向量. 通过每两个坐标轴的平面叫坐标平面,分别称为xOy 平面,yOz 平面,zOx 平面;
