数学分析华东师大定积分

数学分析华东师大定积分 Revised by Jack on December 14,2020

第九章定积分

§1 定积分概念

一问题提出

不定积分和定积分是积分学中的两大基本问题.求不定积分是求导数的逆运算, 定积分则是某种特殊和式的极限, 它们之间既有区别又有联系.现在先从两个例子来看定积分概念是怎样提出来的.

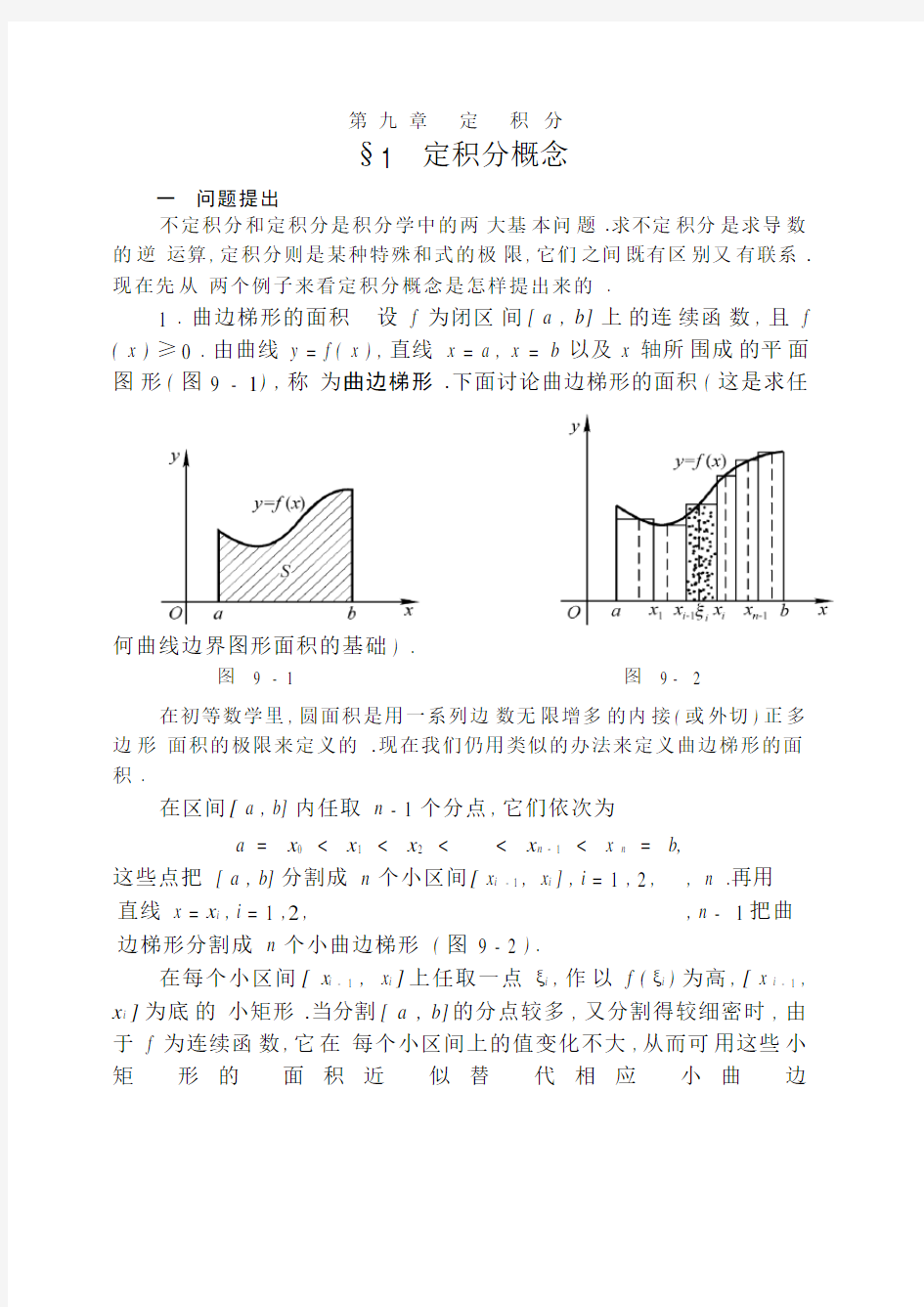
1 . 曲边梯形的面积设 f 为闭区间[ a , b] 上的连续函数, 且 f ( x ) ≥0 . 由曲线y = f ( x ) , 直线x = a , x = b 以及x 轴所围成的平面图形( 图9 - 1) , 称为曲边梯形.下面讨论曲边梯形的面积( 这是求任

何曲线边界图形面积的基础) .

图9 - 1 图9 - 2

在初等数学里, 圆面积是用一系列边数无限增多的内接( 或外切) 正多边形面积的极限来定义的.现在我们仍用类似的办法来定义曲边梯形的面积.

在区间[ a , b] 内任取n - 1 个分点, 它们依次为

a = x0 < x1 < x2 < < x n - 1 < x n = b,

这些点把[ a , b] 分割成n 个小区间[ x i - 1 , x i ] , i = 1 , 2 , , n .再用

直线x = x i , i = 1 , 2, , n - 1把曲边梯形分割成n 个小曲边梯形( 图9 - 2 ) .

在每个小区间[ x i - 1 , x i ]上任取一点ξi , 作以 f (ξi ) 为高, [ x i - 1 , x i ]为底的小矩形.当分割[ a , b] 的分点较多, 又分割得较细密时, 由于 f 为连续函数, 它在每个小区间上的值变化不大, 从而可用这些小矩形的面积近似替代相应小曲边

§1 定积分概念201

梯形的面积.于是, 这n 个小矩形面积之和就可作为该曲边梯形面积S 的近似值,即

n

f (ξi )Δx i (Δx i = x i - x i - 1 ) . ( 1)

S ≈ ∑

i = 1

注意到(1 ) 式右边的和式既依赖于对区间[ a , b]的分割, 又与所有中间点ξi ( i = 1 , 2 , , n ) 的取法有关.可以想象, 当分点无限增多, 且对[ a , b] 无限细分时, 如果此和式与某一常数无限接近, 而且与分点x i 和中间点ξi 的选取无关, 则就把此常数定义作为曲边梯形的面积S .

2 . 变力所作的功设质点受力F 的作

用沿x 轴由点a 移动到点b, 并设 F 处处平行

于x 轴( 图9 - 3 ) .如果F 为常力, 则它对质

点所作的功为W = F( b - a) .现在的问题是, 图9 - 3

F 为变力, 它连续依赖于质点所在位置的坐标x , 即F = F( x) , x ∈[ a , b] 为一连续函数, 此时 F 对质点所作的功W 又该如何计算

由假设F( x ) 为一连续函数, 故在很小的一段位移区间上F( x ) 可以近似地看作一常量.类似于求曲边梯形面积那样, 把[ a , b] 细分为n 个小区间[ x i - 1 , x i ] ,Δx i = x i - x i - 1 , i = 1 , 2 , , n ; 并在每个小区间上任取一点ξi , 就有F( x) ≈F(ξi ) , x ∈[ x i - 1 , x i ] , i = 1 , 2 , , n .

于是, 质点从x i - 1 位移到x i 时, 力 F 所作的功就近似等于F(ξi )Δx i , 从而

n

W ≈∑F(ξi )Δx i . ( 2)

i = 1

同样地, 对[ a , b] 作无限细分时, 若(2 ) 式右边的和式与某一常数无限接近, 则就把此常数定义作为变力所作的功W .

上面两个例子, 一个是计算曲边梯形面积的几何问题, 另一个是求变力作功的力学问题, 它们最终都归结为一个特定形式的和式逼近.在科学技术中还有许多同样类型的数学问题, 解决这类问题的思想方法概括说来就是“分割, 近似求和, 取极限”.这就是产生定积分概念的背景.

二定积分的定义

定义1 设闭区间[ a, b] 内有n - 1 个点, 依次为

a = x0 < x1 < x2 < < x n - 1 < x n = b,

它们把[ a , b] 分成n 个小区间Δi = [ x i - 1 , x i ] , i = 1 , 2 , , n .这些分点或这些闭子区间构成对[ a , b] 的一个分割, 记为

T = { x0 , x1 , , x n } 或{Δ1 ,Δ2 , ,Δn } .

小区间Δi 的长度为Δx i = x i - x i - 1 , 并记

∫

∫

202 第九章 定 积 分

称为分割 T 的模 . ‖ T ‖ = max {Δ x i } ,

1 ≤ i ≤ n

注 由于 Δ x i ≤‖ T ‖ , i = 1 , 2 , , n , 因此 ‖ T ‖可 用来 反映 [ a , b] 被 分 割的细密程度 .另外 , 分割 T 一旦给出 , ‖ T ‖就随之而确定 ; 但是 , 具有同 一细 度‖ T ‖的分割 T 却有无限多个 .

定义 2 设 f 是定义在 [ a , b] 上的 一个 函数 .对于 [ a , b] 的一 个 分割 T = {Δ1 , Δ2 ,

,Δn } , 任取点 ξi ∈Δi ,

i = 1 , 2 , , n , 并作和式n

∑ i = 1

f (ξi )Δ x i .称此和式为函数 f 在 [ a , b] 上的一个积分和 , 也称黎曼和 .

显然 , 积分和既与分割 T 有关 , 又与所选取的点集 {ξi }

有关 . 定义 3 设 f 是定义在 [ a , b] 上的 一个 函数 , J 是一 个确 定的实 数 .若对 任 给的正数 ε, 总存在某一正数 δ, 使得对 [ a , b] 的任何分割 T , 以及在其上任意选 取的点集 {ξ

i

}

, 只要‖ T ‖ <

δ, 就有

n

∑

i = 1

f (ξi

)Δx i

- J < ε,

则称函数 f 在区间 [ a , b] 上可积 或黎 曼可 积 ; 数 J 称为 f 在 [ a , b] 上 的 定积 分

或黎曼积分 , 记作

b

J =

f ( x) d x . ( 3)

a

其中 , f 称为被积函数 , x 称为积分变量 , [ a , b] 称为积分 区间 , a 、b 分别 称为 这 个定积分的下限和上限 .

以上定义 1 至定义 3 是定积分抽象 概念 的完 整叙述 .下 面是 与定积 分概 念 有关的几点补充注释 .

注 1 把定积分定 义的 ε- δ说法和 函数极限 的ε- δ说法相 对照 , 便会 发 现两者有相似的陈述方式 , 因此我们也常用极限符号来表达定积分 , 即把它写作

J = lim

‖ T ‖ → 0

n

∑ i = 1

b

f (ξi

)Δx i

= f ( x )d x . ( 4)

a

然而 , 积 分 和 的 极 限 与 函 数 的 极 限 之 间 其 实 有 着 很 大 的 区 别 : 在 函 数 极 限

lim x → a

f ( x) 中

, 对每一个极限变量 x 来说 , f ( x ) 的值是唯 一确定 的 ; 而 对于积分 和的极限而言 , 每一个‖ T ‖并不唯一对应积分和的一个值 .这使得积 分和的极 限 要比通常的函数极限复杂得多 .

注 2 可积性是函数的又一分析性质 .稍后 ( 定理 9 .3) 就会知道连续函数是 可积的 , 于是本节开头两个实例都可用定积分记号来表示 :

1) 连 续 曲 线 y = f ( x) ≥ 0 在 [ a , b] 上 形 成 的 曲 边 梯 形 面 积 为

∫

∫

∫

i i §1 定积分概念

203

b

S =

f ( x ) d x ; a

2) 在 连 续 变 力 F ( x ) 作 用 下 , 质 点 从 a 位 移 到 b 所 作 的 功 为 W = b

F( x )d x . a 注 3 ( 定积 分的几 何意 义 ) 由 上 述 1) 看到 , 对 于 [ a , b] 上 的 连 续 函 数 f , 当 f ( x) ≥0 , x ∈ [ a , b] 时 , 定积 分 (3 ) 的几 何 意义就是该曲边梯形的面积 ; 当 f ( x ) ≤0 , b

x ∈ [ a , b] 时 , 这 时 J = -

[ - f ( x) ] d x a 是位 于 x 轴 下 方 的 曲 边 梯形面积的 相 反

图 9 - 4

数 , 不妨称之为“ 负面积”; 对于一般非定号的 f ( x ) 而 言 ( 图 9 - 4 ) , 定积 分 J 的

值则是曲线 y = f ( x ) 在 x 轴 上方 部分所 有曲 边梯 形的 正面 积与 下 方部 分所 有 曲边梯形的负面积的代数和 .

注 4 定积分作为积分和的极限 , 它的值只与被积函数 f 和积分区间 [ a, b]

有关 , 而与积分变量所用的符号无关 , 即

b b b

∫f ( x ) d x =∫f ( t ) d t =∫f (θ) d θ =

.

a

a

a

例 1 求 在 区 间 [ 0 , 1 ] 上 , 以抛 物 线 y = x 2

为 曲 边 的 曲 边 三 角 形 的 面 积 ( 图 9 - 5) .

解 由注 3 , 因 y = x 2

在 [ 0 , 1] 上连 续 , 故所 求面积为

1

S =

∫

x 2

d x = lim

n

∑ξ2

Δ

x .0

‖ T ‖ → 0 i = 1

为求得此极限 , 在定 积 分 存 在的 前 提 下 , 允 许 选 择某种特殊的分割 T 和特殊的点集 {ξi } .在此只 需取等分分割 :

T = { 0 , 1 , 2 , , n - 1 , 1} , ‖ T ‖ = 1

;

n i - 1 n n

i - 1 i

n 图 9 - 5

并取 ξi =

n ∈ n , n , i = 1 , 2 , , n .则有n

S = lim ∑ i - 1 · 1 = lim 1 n ( i - 1) 2n → ∞

i = 1 n n n → ∞ 3 ∑ i = 1= lim n → ∞ ( n - 1) n (2 n - 1 ) 1 6 n

3

= 3 .2 n

∫∫∫

204 第九章定积分

习题

1 . 按定积分定义证明∫: b k d x = k( b - a) .

a

2 . 通过对积分区间作等分分割, 并取适当的点集{ξi } , 把定积分看作是对应的积分和的

极限, 来计算下列定积分:

( 1∫)n

x3 d x; 提示: ∑i3 = 1 n2 ( n + 1 )2

0 i= 1 4

1 b

( 2∫)e x d x; (3 ) 0

b

e x d x; a

( 4∫) d x (0 < a < b) .(提示: 取ξ= x x )

a x2 i i - 1 i

§2 牛顿—莱布尼茨公式

从上节例题和习题看到, 通过求积分和的极限来计算定积分一般是很困难的.下面要介绍的牛顿—莱布尼茨公式不仅为定积分计算提供了一个有效的方法, 而且在理论上把定积分与不定积分联系了起来.

定理9 .1若函数 f 在[ a , b]上连续, 且存在原函数 F , 即F′( x ) = f ( x ) ,

x ∈[ a , b] , 则 f 在[ a , b] 上可积, 且

b

f ( x ) d x = F( b) - F( a) . ( 1)

a

这称为牛顿—莱布尼茨公式,它也常写成

b b

f ( x ) d x = F( x) .

a a

证由定积分定义, 任给ε> 0 , 要证存在δ> 0 , 当‖T‖< δ时, 有

n

∑

i = 1

f (ξi )Δx i - [ F( b) - F( a) ]< ε.下面证明满足如此要求的δ确实是存在的.

事实上, 对于[ a , b] 的任一分割T = { a = x0 , x1 , , x n = b} , 在每个小区间[ x i - 1 , x i ]上对F( x) 使用拉格朗日中值定理, 则分别存在ηi ∈( x i - 1 , x i ) , i = 1 , 2 , , n , 使得

n

F( b) - F( a) = ∑[ F( x i ) - F( x i - 1 ) ]

i = 1

n

= ∑

i = 1

n

F′(ηi )Δx i = ∑

i = 1

f (ηi )Δx i . ( 2)

因为 f 在[ a , b]上连续, 从而一致连续, 所以对上述ε> 0 , 存在δ> 0 , 当x′、1

∫

x

∫

∫ §2 牛顿—莱布尼茨公式

205

x ″∈ [ a , b ] 且 | x ′- x ″| < δ时 , 有

f ( x ′) - f ( x ″) < ε

.

b - a

于是 , 当 Δx i ≤‖ T ‖ < δ时 , 任取 ξi ∈ [ x i - 1 , x i ] , 便有 |ξi - ηi | < δ, 这就证得

n

∑ i = 1 f (ξi

)Δ

x i

- [ F ( b) - F ( a) ]

n

=

∑

[ f (ξi

) - f (ηi ) ]Δx i

i = 1

n

≤ ∑ i = 1

f (ξi ) - f (ηi ) Δx i

<

ε

n Δx = ε .·∑ i

i = 1

所以 f 在 [ a , b] 上可积 , 且有公式 (1 ) 成立 .

注 1 在应用牛顿—莱布尼茨公式时 , F( x ) 可由积分法求得 . 注 2 定理条件尚可适当减弱 , 例如 : 1) 对 F 的要 求可 减 弱为 : 在 [ a , b] 上连 续 , 在 ( a , b) 内 可导 , 且 F ′( x ) = f ( x) , x ∈ ( a , b) .这不影响定理的证明 .

2) 对 f 的要 求可 减 弱为 : 在 [ a, b] 上可 积 ( 不 一定 连 续 ) .这 时 ( 2 ) 式 仍 成 b

立 , 且由 f 在 [ a , b] 上可积 , (2 ) 式右 边当 ‖ T ‖→ 0 时的 极限 就是

f ( x ) d x , a

而左边恒为一常数 .( 更一般的情形参见本节习题第 3 题 .)

注 3 至§5 证得连续函数 必有 原函 数之 后 , 本 定理 的条 件中 对 F 的假 设 便是多余的了 .

例 1 利用牛顿—莱布尼茨公式计算下列定积分 :

b

1∫)

2∫) x n d x( n 为正整数 ) ;

a

e x d x; 3 ) a π

d x

(0 < a < b) ; a x 2

24∫) sin x d x;

5 ) 0

x 4 - x 2

d x . 0

解 其中 1 ) — 3) 即为 §1 中 的例题和 习题 , 现在 用牛顿—莱布 尼茨公式 来 计算

就十分方便 :

1∫) b n + 1

x n d x = a n + 1

b

b

= 1 ( b n + 1 - a n + 1 ) .

a

n + 12∫) e x d x = e x

a

b

= e b

- e a

.

a b

3∫

)

d x 1 a

x

2

= -

x

1

1

a

=

a

-

b

.

b b - a b

b

2∫

1 2

2 ∫

206 第九章 定 积 分

4∫)

π sin x d x = - cos x

π = 2 .

( 这是图 9 - 6 所 示 正 弦 曲 线一 拱 下 的 面 积 , 其余各题也可作此联想 .)

5 ) 先 用 不 定 积 分 法 求 出 f ( x ) = x 4 - x 2 的任一原函 数 , 然 后完 成定 积分 计

算 :

图 9 - 6

∫

x

4 - x 2

d x = - 1

2 4 - x 2 d (4 - x 2

) = - 1

3

2 (4 - x 2 ) 3

+ C,

∫

x 4 - x 2

d x = - 1

(4 - x 2 )

3

= 8 .

3

3 例 2 利用定积分求极限 :

lim

n → ∞

1 n + 1 +

1

n + 2 +

+ 1 2 n

= J . 解 把此极限式化为某个积分和的极限式 , 并转化为计算定积分 .为此作如 下变

形 :

n

J = lim ∑

1 ·

1

.

n → ∞ i = 1

1 + i n

n 不难看出 , 其中的和式是函数 f ( x ) = 1

在区间 [ 0 , 1 ] 上 的一 个积分 和 ( 这 里 1 + x

所取的是等分分割 ,Δx i =

1 , ξi = i ∈ i - 1 , i

, i = 1 , 2 , , n ) .所以 n n n n J =∫

d x 0 1 + x

= ln ( 1 + x ) = ln 2 .

当然 , 也可把 J 看作 f ( x) = 1

在 [1 , 2 ] 上的定积分 , 同样有

x

3 J =

∫ d x d x 1 x =∫

2 x - 1

= = ln 2 .习 题

1 . 计算下列定积分 :

1

1

2

( 1∫) ( 2 x + 3) d x; ( 2) 0

1 - x d x ;

0 1 + x

2e 2

1

x

- x

( 3∫) d x ; ( 4) e

x ln x

π e - e d x;

0 2

9( 5∫

)

3

tan x d x;

( 6)

4

x + 1

x

d x;

1

π ∫

x

e

§3 可 积 条 件

207

( 7∫

)

4

d x

e

1 2

; ( 8)

( ln x) d x .0

1 + x

1

2 . 利用定积分求极限 :

( 1) lim 1 (1 + 23 + + n 3

) ;

n → ∞ n 4

( 2) lim

n 1 + 1 + + 1

;n → ∞ ( n + 1) 2 ( n + 2) 2 ( n + n )

2

( 3) lim n 1 + 1 + + 1 ;n → ∞ n 2 + 1 n 2 + 22 2 n

2( 4) lim 1 sin π + sin 2π+ + sin n - 1

.

n → ∞ n n n n

3 . 证明 : 若 f 在 [ a , b ] 上可积 , F 在 [ a , b ] 上连续 , 且除有限个 点外有 F ′( x ) = f ( x ) , 则 有

b

f ( x )d x = F( b) - F( a) . a §3 可 积 条 件

从定理 9 .1 及其后 注 中看 到 , 要 判 别一 个 函数 是 否 可积 , 必须 研 究可 积 条

件 .

一 可积的必要条件

定理 9 .2 若函数 f 在 [ a , b] 上可积 , 则 f 在 [ a , b] 上必定有界 . 证 用反证法 .若 f 在 [ a , b] 上 无界 , 则对 于 [ a , b] 的 任一 分割 T , 必存 在 属于 T 的某个小区间Δk , f 在 Δk 上无界 .在 i ≠ k 的各个小区间 Δi 上任意取定 ξi , 并记

G =

∑

f (ξi

)Δx i

.

i ≠ k

现对任意大的正数 M , 由于 f 在 Δk 上无界 , 故存在 ξk ∈Δk , 使得

于是有

f (ξk ) > M + G Δx k

n

∑ i = 1

f (ξi

)Δ x

i

≥ f (ξk )Δx k - ∑ f (ξi )Δ

x i i ≠ k

> M + G ·Δ x k - G = M .

Δx k

由此可见 , 对于无论多小的‖ T ‖ , 按上 述 方法 选取 点集 {ξi } 时 , 总 能使 积分 和 的绝对值大于任何预先给出的正数 , 这与 f 在 [ a, b] 上可积相矛盾 .

.

208 第九章 定 积 分

这个定理指出 , 任何可积函数一 定是 有界的 ; 但要注 意 , 有界 函数却 不一 定 可积 .

例 1 证明狄利克雷函数在 [0 , 1 ] 上有界但不可积 .

D( x) =

1 , x 为有理数 , 0 , x 为无理数

证 显然 | D( x ) | ≤1 , x ∈ [0 , 1 ] . 对于 [0 , 1 ] 的任一分割 T , 由有理数和无 理数在 实数中的 稠密性 , 在属 于 T

n

n

的任一小区间 Δi 上 , 当取 ξi 全为有理数时 , ∑ D(ξi )Δ

x i = ∑Δ x i = 1 ; 当 取i = 1

n

i = 1

ξi 全为无理数时 , ∑ D(ξi )Δ x i = 0 .所以不论 ‖ T ‖ 多 么小 , 只要点集 {ξi } 取

i = 1

法不同 ( 全取有理数或全取无理数 ) , 积分和有不同 极限 , 即 D( x) 在 [ 0 , 1] 上 不 可积 .

由此例可见 , 有界是可积的必要 条件 .所 以在 以后讨 论函 数的可 积性 时 , 总 是首先假设函数是有界的 , 今后不再一一申明 .

二 可积的充要条件

要判断一个函数是否可积 , 固然可以根据定义 , 直接考察积分和是否能无限 接近某一常数 , 但由于积分和的复杂性和那个常数不易预知 , 因此这是极其困难 的 .下面即将给出的可积准则只与被积函数本身有关 , 而不涉及定积分的值 .

设 T = {Δi | i = 1 , 2 , , n} 为对 [ a , b] 的任一分割 .由 f 在 [ a , b] 上有界 , 它 在每个 Δi 上存在上、下确界 :

M i = sup f ( x) , m i = inf f ( x ) , i = 1 , 2 ,

, n .

x ∈ Δ

i

作和

x ∈Δ

i

n

S( T ) = ∑ i = 1

n

M i Δ x i , s( T) =

∑

i = 1

m i

Δx i

,分别称为 f 关于 分 割 T 的 上 和 与 下 和 ( 或 称 达 布 上 和 与 达 布 下 和 , 统 称 达 布

和 ) .任给 ξi ∈

Δi , i = 1 , 2 , , n , 显然有n

s( T ) ≤ ∑

i = 1

f (ξi )Δ x i ≤ S ( T ) . ( 1)

与积分和相比较 , 达布和只与分割 T 有关 , 而与点 集 {ξi } 无关 .由不等 式 ( 1 ) , 就 能通过讨论上和与下和当‖ T ‖→0 时的极限来揭示 f 在 [ a , b] 上是否可积 .所 以 , 可积性理论总是从讨论上和与下和的性质入手的 .

定理 9 .3 ( 可积准则 ) 函数 f 在 [ a , b] 上可积的充要条件是 : 任给 ε> 0 ,

i i i

i i §3 可 积 条 件

209

总存在相应的一个分割 T , 使得

S( T ) - s( T) < ε .

( 2)

本定理的证明依赖对上和与下和性质的详尽讨论 , 这里从略 ( 完整证明补述 于

§6) .

设 ω = M - m , 称为 f 在 Δ 上的振幅 , 有必要时也记为 ωf

.由于 n

S( T ) - s( T ) = ∑ωi Δx i ( 或记为∑ωi Δ

x i ) ,因此可积准则又可改述如下 :

i = 1

T

定理 9 .3′ 函数 f 在 [ a , b] 上 可 积的 充要 条件 是 : 任 给 ε> 0 , 总存 在相 应

的某一分割 T , 使得

∑ωi

Δ

x i

< ε . ( 2′)

T

不等式 (2 ) 或 ( 2′) 的几 何意 义 是 : 若 f 在

[ a , b] 上 可 积 , 则 图 9 - 7 中 包 围 曲 线 y = f ( x) 的一系列小矩形面积之和可以达到 任意 小 , 只要分割充分地细 ; 反之亦然 .

三 可积

函

数类

根据可 积 的 充 要 条 件 , 我 们 证 明 下 面 一 些类 型 的 函 数 是 可 积 的 ( 即 可 积 的 充 分 条 件 ) .

图 9 - 7

定理 9 .4 若 f 为 [ a , b] 上的连续函数 , 则 f 在 [ a , b] 上可积 .

证 由于 f 在闭区间 [ a , b] 上 连续 , 因 此在 [ a , b] 上 一致 连续 .这就 是说 , 任给 ε> 0 , 存在 δ> 0 , 对 [ a, b ] 中任意两点 x ′、x ″, 只要 | x ′- x ″| < δ, 便有

f ( x ′) - f ( x ″) < ε

.

b - a 所以只要对 [ a , b] 所 作 的分 割 T 满足 ‖ T ‖ < δ, 在 T 所 属 的任 一 小区 间 Δi 上 , 就能使 f 的振幅满足

从而导致

ωi = M i - m i = sup x ′, x ″∈ Δ i

| f ( x ′) - f ( x ″) | ①

ε ε

b - a ,

∑ωi

Δx

i

≤ b - a ∑Δ x i = ε . T T

由定理 9 .2′证得 f 在 [ a , b ] 上可积 .

①

此 等式成 立的 证明留 作本节 习题 ( 第 5 题 ) .

≤

2

210 第九章 定 积 分

读者应该注意到 , 一致连续性在本定理证明中所起的重要作用 .

定理 9 .5 若 f 是区间 [ a, b]上只有有限个间断点的有界函数 , 则 f 在 [ a, b]

上可积 .

证 不失一般性 , 这里只证明 f 在 [ a , b] 上仅有一个间断点的情形 , 并假 设 该间断点即为端点 b .

任给 ε> 0 , 取 δ′满足 0 < δ′<

ε

2 ( M - m) < b - a , 其中 M 与 m 分别为 f 在

[ a , b] 上的上确界与下确界 ( 设 m < M , 否则 f 为常量函数 , 显然 可积 ) .记 f 在 小区间 Δ′= [ b - δ′, b ] 上的振幅为 ω′, 则

ω′δ′< ( M - m) · ε 2 ( M - m) = ε

.

2

因为 f 在 [ a , b - δ′] 上连续 , 由 定理 9 .3 知 f 在 [ a , b - δ′] 上 可积 .再 由定 理 9 .2′( 必要性 ) , 存在对 [ a , b - δ′] 的某个分割 T ′= {Δ1 ,Δ2 ,

,Δn - 1 } , 使得 ε

∑ωi

Δ

x i

<

.

T ′

令Δn =Δ′, 则 T = {Δ1 ,Δ2 ,

, Δn - 1 ,Δn } 是对 [ a , b ] 的一个分割 , 对于 T , 有

∑ωi Δx i = ∑ωi Δ x i + ω′δ′< ε ε

2 + 2 = ε .T T ′

根据定理 9 .2′( 充分性 ) , 证得 f 在 [ a , b ] 上可积 .

定理 9 .6 若 f 是 [ a , b] 上的单调函数 , 则 f 在 [ a , b] 上可积 . 证 设 f 为增函数 , 且 f ( a ) < f ( b) ( 若 f ( a ) = f ( b) , 则 f 为常量 函数 , 显 然可积 ) .对 [ a , b] 的任一分割 T , 由 f 的增 性 , f 在 T 所属的 每个 小区 间 Δi 上 的振幅为

ωi = f ( x i ) - f ( x i - 1 ) ,

于是有

n

∑ωi

Δx i

≤ ∑

[ f ( x i

) - f ( x i - 1 ) ] ‖ T ‖

T

i = 1

= [ f ( b) - f ( a) ] ‖ T ‖ .

由此可见 , 任给 ε> 0 , 只要‖ T ‖ <

ε

, 这时就有

f ( b) - f ( a )

∑ωi

Δ

x i

< ε,

T

所以 f 在 [ a , b] 上可积 .

注意 , 单调函数即使有无限多个间断点 , 仍不失其可积性 .

例 2 试用两种方法证明函数

0 ,

x = 0 ,

f ( x) = 1

n

, 1

n + 1 < x ≤ 1

n

, n = 1 , 2 ,

∫

ε

2

§3 可 积 条 件

211

在区间 [0 , 1 ] 上可积 .

证 [ 证法一 ] 由 于 f 是 一增函数 ( 图 9 - 8) ,

虽然它在 [0 , 1 ] 上有无限多个间断点 x n = 1

, n = 2 ,

n

3 , , 但由定理 9 .5 , 仍保证它在 [0 , 1] 上可积 .

[ 证法二 ] ( 仅利用定理 9 .2′和定理 9 .4 ) 任给

ε> 0 , 由于 lim 1 = 0 , 因此当 n 充分大时 1 < ε

, 这

n → ∞

n

n 2

说明 f 在

ε, 1 上 只 有 有 限 个 间 断 点 .利 用 定 理

2

9 .4 和定理 9 .2′推知 f 在

ε

, 1 上可 积 , 且存 在对

2

图 9 - 8

ε

2

, 1 的某一分割 T ′, 使得

∑ωi Δ

x i < . T ′

再把小区间 0 ,

ε

2 与 T ′合并 , 成为对 [ 0 , 1 ] 的一 个分 割 T .由于 f 在 0 , ε

上

2

的振幅 ω0 < 1 , 因此得到

ε

ε

ε

∑ωi

Δ

x i

= ω0 · 2 + ∑ωi Δ

x i < 2 + 2 = ε . T

T ′

所以 f 在 [0 , 1 ] 上可积 .

事实上 , 例 2 的第二种证法并不限于该例中的具体函数 , 更一般的命题见本 节习题第 4 题 .下面例 3 的证明思想与它可谓异曲同工 .

例 3 证明黎曼函数

f ( x ) = 1 q

, x = p

q

, p 、q 互素 , q > p ,

在区间 [0 , 1 ] 上可积 , 且 0 ,

x = 0 , 1 以及 (0 , 1 ) 内的无理数

1

f ( x) d x = 0 . 0 分析 已 知 黎曼 函 数 在 x = 0 , 1 以 及一切无理 点处 连续 , 而 在 ( 0 , 1 ) 内 的 一 切有理点处 间断 .证 明它 在 [ 0 , 1 ] 上 可 积 的直观

构思如下 : 如图 9 - 9 所示 , 在黎 曼

函数的图象中画一条水平直线 y = ε

.在

2

图 9 - 9 此直线上方只有函数图象中有限个点 , 这

些点所对应的自变量可被含于属于分割 T 的有限 个小区间 中 , 当‖ T ‖足够

小

T

于ε 1

ε

2

212 第九章 定 积 分

时 , 这有限个小区间的总长 可为任 意小 ; 而 T 中 其余 小区间 上函 数 的振 幅不 大

2

, 把这两部分相合 , 便可证得 ∑ωi

Δx

i

< ε .下面写出这个证明 .

证 任给 ε> 0 , 在 [0 , 1 ] 内 使得

1

>

ε

的有 理 点 p 只 有有 限个 , 设它 们 为

q 2

q

ε

r 1 , , r k .现对 [ 0 , 1] 作分割 T = {Δ1 ,Δ2 , ,Δn } , 使‖ T ‖ < 2 k

, 并把 T 中所有

小区间分为 {Δ′i | i = 1 , 2 , , m } 和 {Δ″i | i = 1 , 2 , , n - m } 两 类 .其中 {Δ′i } 为 含有 { r i | i = 1 , 2 , , k} 中点的 所有小区 间 , 这类小 区间的个 数 m ≤ 2 k( 当所 有 r i 恰好都是 T 的分割点时才有 m = 2 k ) ; 而 {Δ″i } 为 T 中所

有其余不 含 { r i } 中 点的小区间 .由于 f 在 Δ′i 上的振幅 ω′i ≤ 1

2 , 于是

m

∑

ω′i Δ x ′i ≤ 1 m Δ x ′i ≤ 1 ·2 k ‖ T ‖ < ;i = 1

∑

i = 1

ε

而 f 在 Δ″i 上的振幅 ω″i ≤ 2 , 于是

n - m

n - m

ε ε

∑ω″i

Δ x ″i

≤ i = 1

把这两部分合起来 , 便证得

∑Δ x ″i

< .

i = 1

n

m

n - m

∑ωi

Δx

i

= ∑ω′i Δx ′i + ∑ω″i Δx ″i <

ε,i = 1

即 f 在 [0 , 1 ] 上可积 .

i = 1

i = 1

因为已经证得 f 在 [0 , 1 ] 上可积 , 所 以当取 ξi 全为无 理点时 , 使 f (ξi ) = 0

, 从而

n

∫

f ( x ) d x = lim ∑ f (ξi )Δ

x i = 0 . 0

‖ T ‖ → 0 i = 1

习 题

1 . 证明: 若 T ′是 T 增加若干个分点后所得的分割 , 则 ∑ω′i Δx ′i ≤ ∑ωi Δ

x i . T ′

T

2 . 证明: 若 f 在 [ a , b]上可积 , [α,β] ì [ a , b] , 则 f 在[α,β]上也可积 .

3 . 设 f 、g 均为定义在[ a, b]上的有界函数 .证明:若仅在[ a, b]中有限个点处 f ( x)≠ g( x) , b b

则当 f 在[ a , b ] 上可积时 , g 在[ a , b ] 上也可积 , 且

∫f ( x ) d x =∫g( x )d x .

a

a

4 . 设 f 在[ a , b] 上有界 , { a n } ì [ a , b] , lim a n = c .证明 :若 f 在 [ a , b] 上只有 a n ( n = 1 , n → ∞

2 ,

) 为其间断点 , 则 f 在 [ a , b] 上可积 . 5 . 证明: 若 f 在区间 Δ上有界 , 则

sup x ∈Δ

f ( x ) - inf x ∈Δ

f ( x ) = sup x ′, x ″∈Δ

| f ( x ′

) - f ( x ″) | .2 2

2

2

∫∫∫

a

a

∫

§4 定积分的性质213§4 定积分的性质

一定积分的基本性质

性质1 若f 在[ a , b] 上可积, k 为常数, 则k f 在[ a , b] 上也可积, 且

b

k f ( x ) d x = k

a

证当k = 0 时结论显然成立.

当k≠0 时, 由于

n b

f ( x) d x . ( 1) a

n

∑k f (ξi )Δx i - kJ = | k |·∑f (ξi )Δx i - J ,

i = 1

b

i = 1

其中J = f ( x ) d x , 因此当 f 在[ a , b] 上可积时, 由定义, 任给ε>0 , 存在δ> a

0 , 当‖T‖< δ时,

n

∑

i = 1 从而f (ξi )Δx i - J <

ε

| k |

,

即k f 在[ a , b] 上可积, 且

b

n

∑

i = 1

kf (ξi )Δx i - kJ < ε.

b

∫k f ( x ) d x = kJ = ∫k f ( x) d x .

a

性质2 若f 、g都在[ a , b] 上可积, 则 f ±g 在[ a , b] 上也可积, 且

b b b

∫[f ( x ) ±g( x ) ]d x =∫f ( x) d x ±∫g( x ) d x . ( 2)

a a a

证明与性质1 类同, 留给读者.

性质1 与性质2 是定积分的线性性质, 合起来即为

b

∫[αf ( x ) + βg ( x ) ]d x = ∫α其中α、β为常数. b

f ( x) d x + β

a

b

g( x )d x ,

a

性质3 若f 、g都在[ a , b] 上可积, 则f·g 在[ a, b] 上也可积. 证由f 、g都在[ a , b] 上可积, 从而都有界, 设

A = sup

x ∈ [ a , b] f ( x ) , B = sup

x ∈ [ a , b]

g( x) ,

且 A > 0 , B > 0 ( 否则 f 、g中至少有一个恒为零值函数, 于是f·g 亦为零值函数, 结论显然成立) .

任给ε> 0 , 由 f 、g 可积, 必分别存在分割T′、T″, 使得

i i

i i 2 ∑ ∑ 214

第九章 定 积 分

∑ωf

ε εi Δ x i <

T ′ , ωg

Δx i 2 B T ″

< 2 A .

令 T = T ′+ T ″( 表示把 T ′、T ″的所有分割点合并而成的一个新的分割 T ) .对于

[ a , b] 上 T 所属的每一个 Δi , 有

ωf · g i = sup x ′, x ″∈Δ

i

≤ sup

x ′, x ″∈Δ i

f ( x ′) g( x ′) - f ( x ″) g( x ″)

[ g( x ′) · f ( x ′) - f ( x ″) + f ( x ″) · g( x ′) - g( x ″) ]

≤ B ωf

+ A ωg

.

利用§3 习题第 1 题 , 可知

∑ω

f ·

g f

g

i

Δx i ≤ B ∑ωi Δ x i + A ∑ωi Δx i

T

T

T

∑ωg

Δx T ′

T ″

< B · ε 2 B + A · ε

2 A

= ε,

这就证得 f ·g 在 [ a , b] 上可积 .

b b b

注意 , 在一般情形下

∫f ( x ) g( x ) d x ≠∫f ( x ) d x ·∫g( x ) d x .

a

a

a

性质 4 f 在 [ a , b] 上可 积 的充 要 条件 是 : 任给 c ∈ ( a , b ) , f 在 [ a , c] 与 [ c, b] 上都可积 .此时又有等式

b

c

b

∫ f ( x ) d x =∫f ( x ) d x +∫

f ( x ) d x . ( 3)

a

a

c

证 [ 充分性 ] 由于 f 在 [ a , c] 与 [ c, b] 上都可积 , 故任 给 ε> 0 , 分别存 在 对 [ a , c ] 与 [ c, b ] 的分割 T ′与 T ″, 使得

∑ω′i Δx ′i < T ′ ε ε , ω″i Δx ″i < . T ″

2现令 T = T ′+ T ″, 它是对 [ a , b ] 的一个分割 , 且有

∑ωi

Δ

x i

= ∑ω′i Δ x ′i + ∑ω″i Δx ″i <

ε . T

T ′

T ″

由此证得 f 在 [ a , b] 上可积 .

[ 必要性 ] 已知 f 在 [ a , b] 上可积 , 故任给 ε > 0 , 存在对 [ a , b] 的某分割

T , 使得∑ωi Δx i < ε

.在 T 上再增加一个分点 c, 得到一个新的分割 T .由 §3T

习题第 1 题 , 又有

i

Δ x i ≤ ∑ωi Δ

x i < ε . T *

T

分割 T *

在 [ a, c] 和 [ c, b] 上的部分 , 分别 构成对 [ a , c] 和 [ c, b] 的分 割 , 记 为 T ′和 T ″, 则有

i

i

i

*

∑ω′i Δx ′i ≤ ∑ω ∑ω″i Δx ″i ≤ ∑ω ∫

∫ ∫

∫

b i i i

i §4 定积分的性质

215

* Δx * < ε,

T ′

T *

* Δx *

< ε .

T ″

T *

这就证得 f 在 [ a , b] 与 [ b, c] 上都可积 .

在证得上面结果 的基础 上最后来 证明等式 ( 3 ) .为此对 [ a , b] 作分 割 T , 恒 使点 c 为其中的一个分点 , 这时 T 在 [ a , c] 与 [ c, b] 上的部分各自构成对 [ a , c]

与 [ c, b ] 的分割 , 分别记为 T ′与 T ″.由于

∑

f (ξi

)Δx i

= ∑ f (ξ′i )Δx ′i + ∑ f (ξ″i )Δx ″i ,

T

T ′

T ″

因此当‖ T ‖→0( 同时有‖ T ′‖→ 0 , ‖ T ″‖→ 0) 时 , 对上式 取极限 , 就得到 ( 3)

式成立 .

性质 4 及公 式 ( 3 ) 称 为 关 于 积 分 区 间 的 可加性 .当 f ( x ) ≥ 0 时 , (3 ) 式的 几何 意义 就 是曲边梯形面积的可 加性 .如 图 9 - 10 所示 , 曲边 梯 形 AabB 的 面 积 等 于 曲 边 梯 形 AacC 的面积与 CcbB 的面积之和 .

b

按定积分的定义 , 记号

f ( x )d x 只 有当 a a < b 时才有意义 , 而当 a = b 或 a > b 时 本来 是没有意义的 .但为了运用上的方便 , 对它作如下规定 :

a

规定 1 当 a = b 时 , 令

f ( x ) d x = 0; a

图 9 - 10

b

a

规定 2 当 a > b 时 , 令∫ f ( x ) d x = -∫ f ( x )d x . a

b

有了这个规定之后 , 等式 ( 3) 对于 a 、b 、c 的 任何 大小 顺序 都 能成 立 .例如 , 当 a < b < c 时 , 只要 f 在 [ a, c] 上可积 , 则有

c

b

b

c

c

∫f ( x ) d x +∫f ( x ) d x = ∫

f ( x ) d x +∫f ( x )d x -∫f ( x ) d x a

c

a

b

b

b = f ( x ) d x . a

性质 5 设 f 为 [ a , b] 上的可积函数 .若 f ( x) ≥0 , x ∈ [ a , b] , 则

b

f ( x ) d x ≥ 0 . ( 4)

a 证 由于在 [ a , b] 上 f ( x) ≥ 0 , 因此 f 的任一 积分和都 为非负 .由 f 在 [ a ,

b] 上可积 , 则有

∫f ( x) d x =

lim

n

∑

f (ξi

)Δ x i

≥ 0 .

a

‖ T ‖ → 0 i = 1

i

∫ ∫ ∫ ∫

∫ ∫ 216 第九章 定 积 分

推论( 积分不等式性 ) 若 f 与 g 为[ a, b]上的两个可积函数 , 且 f ( x) ≤ g( x) , x ∈ [ a , b] , 则有

b

b

∫ f ( x ) d x ≤∫g( x ) d x .

( 5)

a

a

证 令 F( x ) = g ( x ) - f ( x ) ≥0 , x ∈ [ a , b] , 由性质 2 知道 F 在 [ a , b] 上 可积 , 且由性质 5 推得

b b b

0 ≤

∫F ( x ) d x =∫g( x ) d x ∫

- f ( x ) d x ,a

a

a

不等式 (5 ) 得证 .

性质 6 若 f 在 [ a , b] 上可积 , 则 | f | 在 [ a , b] 上也可积 , 且

b

b

∫ f ( x ) d x ≤∫ f ( x )

d x . ( 6)

a

a

证 由于 f 在 [ a, b ]上可积 , 故任给 ε> 0 , 存在某分割 T , 使得 ∑ωf Δx < ε.由绝对值不等式

T

f ( x ′) - f ( x ″)

≤ f ( x ′) - f ( x ″) ,

可得 ω| f |

f

i ≤ωi , 于是有

∑ω

| f | f

i

Δx i ≤ ∑ωi Δ x i < ε .

T

T

从而证得 | f | 在 [ a, b] 上可积 .

再由不等式 - | f ( x ) | ≤ f ( x) ≤ | f ( x ) | , 应用 性质 5 ( 推论 ) , 即 证得不等 式 (6 ) 成立 .

注意 这个性质的逆命题一般不成立 , 例如

1 , x 为有理数 ,f ( x ) =

- 1 ,

x 为无理数

在 [0 , 1 ] 上不可积 ( 类似于狄利克雷函数 ) ; 但 | f ( x ) | ≡1 , 它在 [0 , 1 ] 上可积 .

1

例 1 求

- 1

f ( x) d x , 其中 f ( x) =

2 x - 1 , - 1 ≤ x < 0 , e - x

,

0 ≤ x ≤ 1 .

解 对于分段函数的定积分 , 通常利用积分区间可加性来计算 , 即

1 0

f ( x ) d x = - 1

- 1

1 f ( x) d x + f ( x )d x 0

0 1 = (2 x - 1) d x + e - x

d x

- 1

= ( x 2

- x )

0 1

+ ( - e

- x

)

- 1

i