定积分与微积分基本定理

教学过程一、课堂导入
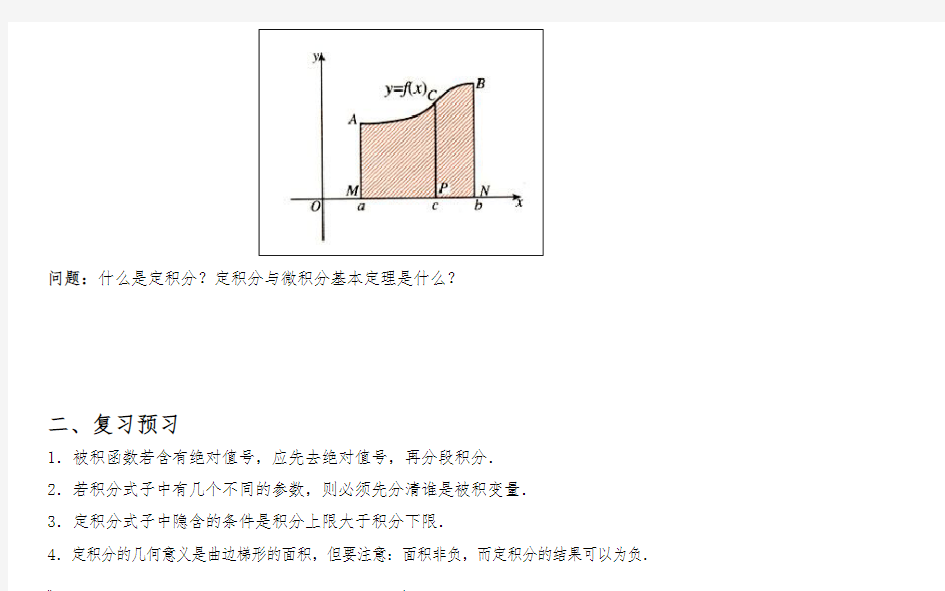
问题:什么是定积分?定积分与微积分基本定理是什么?
二、复习预习
1.被积函数若含有绝对值号,应先去绝对值号,再分段积分.
2.若积分式子中有几个不同的参数,则必须先分清谁是被积变量.
3.定积分式子中隐含的条件是积分上限大于积分下限.
4.定积分的几何意义是曲边梯形的面积,但要注意:面积非负,而定积分的结果可以为负.
5.将要求面积的图形进行科学而准确的划分,可使面积的求解变得简捷.
三、知识讲解
考点1 定积分的概念
设函数y =f (x )定义在区间[a ,b ]上用分点a =x 0 近于0,在每个小区间任取一点ξi ,作和式I n =∑n -1 i =0 f (ξi )Δx i .当λ→0时,如果和式的极限存在,把和式I n 的极限叫做函数f (x )在区间[a ,b ]上的定积分,记作?b a f (x )d x ,即?b a f (x )d x =lim λ→0∑n -1 i =0f (ξi )Δx i ,其中f (x )叫做被积函数,f (x )d x 叫做被积式,a 为积分下限,b 为积分上限. (1)?b a kf(x)d x=k?b a f(x)d x (k为常数). (2)?b a[f(x)±g(x)]d x=?b a f(x)d x±?b a g(x)d x. (3)?b a f(x)d x=?c a f(x)d x+?b c f(x)d x (a 如果F′(x)=f(x),且f(x)在[a,b]上可积,则?b a f(x)d x=F(b)-F(a).其中F(x)叫做f(x)的一个原函数. 四、例题精析 考点一定积分的计算 例1 若定积分?m -2-x2-2x d x= π 4 ,则m等于 ( ) A.-1 B.0 C.1 D.2 定积分与微积分基本定理(理) 基础巩固强化 1.求曲线y =x 2与y =x 所围成图形的面积,其中正确的是( ) A .S =?? ?0 1(x 2-x )d x B .S =?? ?0 1 (x -x 2)d x C .S =?? ?0 1 (y 2-y )d y D .S =??? 1 (y - y )d y [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解析] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x ≥x 2,故函数y =x 2与y =x 所围成图 形的面积S =?? ?0 1 (x -x 2)d x . 2.如图,阴影部分面积等于( ) A .2 3 B .2-3 [答案] C [解析] 图中阴影部分面积为 S =??? -3 1 (3-x 2 -2x )d x =(3x -1 3x 3-x 2)|1 -3=32 3. 4-x 2d x =( ) A .4π B .2π C .π [答案] C [解析] 令y =4-x 2,则x 2+y 2=4(y ≥0),由定积分的几何意义知所求积分为图中阴影部分的面积, ∴S =1 4×π×22=π. 4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为v 甲和v 乙(如图所示).那么对于图中给定的t 0和t 1,下列判断中一定正确的是( ) A .在t 1时刻,甲车在乙车前面 B .在t 1时刻,甲车在乙车后面 C .在t 0时刻,两车的位置相同 D .t 0时刻后,乙车在甲车前面 [答案] A [解析] 判断甲、乙两车谁在前,谁在后的问题,实际上是判断在t 0,t 1时刻,甲、乙两车行驶路程的大小问题.根据定积分的几何意义知:车在某段时间内行驶的路程就是该时间段内速度函数的定积 1.6 微积分基本定理( 2) 一、【教学目标】 重点:使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分. 难点:利用微积分基本定理求积分;找到被积函数的原函数. 能力点:正确运用基本定理计算简单的定积分. 教育点:通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩 证唯物主义观点,提高理性思维能力. 自主探究点:通过实例探求微分与定积分间的关系,体会微积分基本定理的重要意义. 易错点:准确找到被积函数的原函数,积分上限与下限代人求差注意步骤,以免符号出错. 考试点:高考多以填空题出现,以考查定积分的求法和面积的计算为主. 二、【知识梳理】 1. 定积分定义:如果函数() f x在区间[,] a b上连续,用分点 0121- =<<<<<<<= i i n a x x x x x x b,将区间[,] a b等分成n个小区间,在每一个小区间 1 [,] i i x x - 上任取一点(1,2,,) ξ= i i n,作和 1 ()() ξξ = - ?=∑n i i i i b a f x f n ,当n→∞时,上述和式无限接近某个常数,这个常数叫做函数() f x在区间[,] a b上的定积分,记作() b a f x dx ?,即 1 ()lim() n b a i n i b a f x dx f n ξ →∞ = - =∑ ?,这里a、b分别叫做积分的下限与上限,区间[,] a b叫做积分区间,函数() f x叫做被积函数,x叫做积分变量,() f x dx叫做被积式. 2.定积分的几何意义 如果在区间[,] a b上函数连续且恒有()0 f x≥,那么定积分() b a f x dx ?表示由直线, x a x b ==(a b ≠),0 y=和曲线() y f x =所围成的曲边梯形的面积. 微积分基本定理 一、教材分析 1、教材的地位及作用 微积分基本定理是普通高中课程标准实验教科书(人教版)高二年级数学(选修2-2)第一章第六节内容,本节内容共设计两个课时,这是第一课时,这节课的主要内容是微积分基本公式的导出以及用它求定积分。 本节课是学生学习了导数和定积分这两个概念后的学习,它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。 2、教学目标 根据学生的认知结构特征以及教材内容的特点,依据新课程标准要求,确定本节课的教学目标如下: (1)知识与技能目标:通过实例,直观了解微积分基本定理的含义,会求简单的定积分。 (2)过程与方法目标:通过实例体会用微积分基本定理求定积分的方法。 (3)情感、态度与价值观目标:通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力。 3、教学重点、难点 重点:通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分。(根据教材内容特点及教学目标的要求) 难点:了解微积分基本定理的含义。(根据学生的年龄结构特征和心理认知特点) ——以学生现有的知识水平对于微积分基本定理的严密证明是存在着一定难度的,而突破难点的关键在于让学生主动去探索,体会微积分基本公式的导出以及利用它来计算简单的定积分,这样才能从真正意义上把握该定理的含义,提高学生的能力,体现学生的主体地位。 二、教法和学法 1、教法: 素质教育理论明确要求:教师是主导,学生是主体,只有教师在教学过程中注重引导,才能充分发挥学生的主观能动性,有利于学生创造性思维的培养和能力的提高,根据本节的教学内容及教学目标和学生的认识规律,我采用类比、启发、引导、探索式相结合的方法,启发、 1.4定积分与微积分基本定理练习题及答案 1.(2011·一中月考)求曲线y =x2与y =x 所围成图形的面积,其中正确的是( ) A .S =??01(x2-x)dx B .S =??01(x -x2)dx C .S =??01(y2-y)dy D .S =??01(y -y)dy [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解读] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x ≥x2,故函数y =x2与y =x 所围成图形的面积S =??0 1(x -x2)dx. 2.(2010·日照模考)a =??02xdx ,b =??02exdx ,c =??02sinxdx ,则a 、b 、c 的大小关系是 ( ) A .a 1.6 微积分基本定理 一、教学目标 知识与技能目标 通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分 过程与方法 通过实例体会用微积分基本定理求定积分的方法 情感态度与价值观 通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力。 二、教学重难点 重点 通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分。 难点 了解微积分基本定理的含义 三、教学过程 1、复习: 定积分的概念及用定义计算 2、引入新课 我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法。 变速直线运动中位置函数与速度函数之间的联系 设一物体沿直线作变速运动,在时刻t 时物体所在位置为S(t),速度为v(t)(()v t o ≥), 则物体在时间间隔12[,]T T 内经过的路程可用速度函数表示为 21()T T v t dt ?。 另一方面,这段路程还可以通过位置函数S (t )在12[,]T T 上的增量12()()S T S T -来表达,即 2 1()T T v t dt ?=12()()S T S T - 而()()S t v t '=。 对于一般函数()f x ,设()()F x f x '=,是否也有 ()()()b a f x dx F b F a =-? 若上式成立,我们就找到了用()f x 的原函数(即满足()()F x f x '=)的数值差()()F b F a -来计算()f x 在[,]a b 上的定积分的方法。 注:1:定理 如果函数()F x 是[,]a b 上的连续函数()f x 的任意一个原函数,则 ()()()b a f x dx F b F a =-? 证明:因为()x Φ=()x a f t dt ?与()F x 都是()f x 的原函数,故 ()F x -()x Φ=C (a x b ≤≤) 其中C 为某一常数。 令x a =得()F a -()a Φ=C ,且()a Φ= ()a a f t dt ?=0 即有C=()F a ,故()F x =()x Φ+()F a ∴ ()x Φ=()F x -()F a =()x a f t dt ? 令x b =,有()()()b a f x dx F b F a =-? 此处并不要求学生理解证明的过程 为了方便起见,还常用()|b a F x 表示()()F b F a -,即 ()()|()()b b a a f x dx F x F b F a ==-? 该式称之为微积分基本公式或牛顿—莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。 它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。 例1.计算下列定积分: (1)2 11dx x ?; (2)3211(2)x dx x -?。 解:(1)因为'1(ln )x x =, 所以22111ln |ln 2ln1ln 2dx x x ==-=?。 (2))因为2''211()2,()x x x x ==-, 所以3332211111(2)2x dx xdx dx x x -=-??? 233111122||(91)(1)33x x =+=-+-=。 练习:计算 120x dx ? 解:由于313 x 是2x 的一个原函数,所以根据牛顿—莱布尼兹公式有 120x dx ?=3101|3x =33111033?-?=13 例2.计算下列定积分:1-定积分与微积分基本定理(理)含答案版
微积分基本定理(17)
微积分基本定理
定积分及微积分基本定理练习题及答案
高中数学选修2-2公开课教案16微积分基本定理
7.微积分基本定理练习题
