三角函数常用公式表
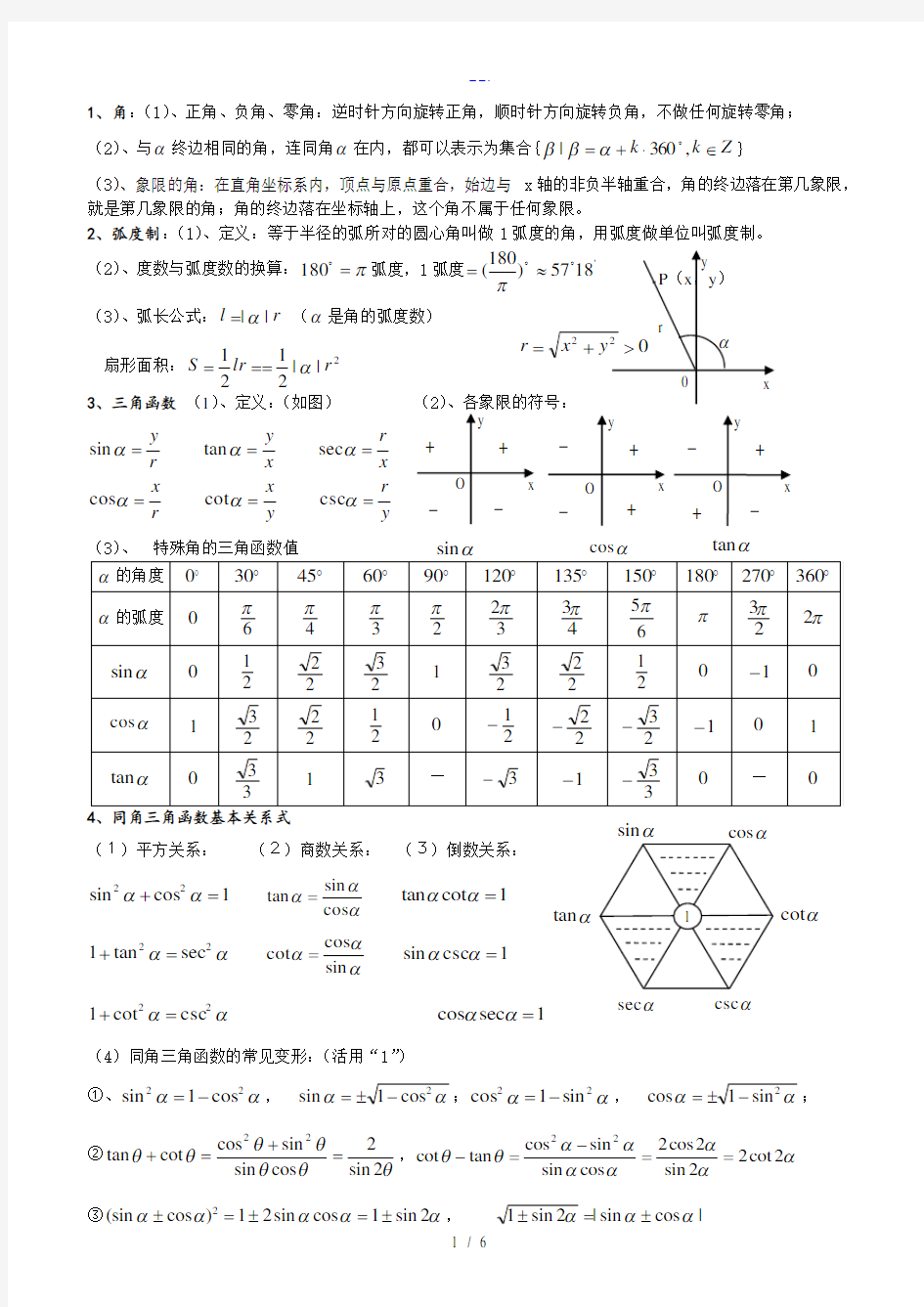

1、角:(1)、正角、负角、零角:逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角; (2)、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈?+=,360|
αββ}
(3)、象限的角:在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角;角的终边落在坐标轴上,这个角不属于任何象限。 2、弧度制:(1)、定义:等于半径的弧所对的圆心角叫做1弧度的角,用弧度做单位叫弧度制。 (2)、度数与弧度数的换算:π=
180弧度,1弧度
)180
( =π
(3)、弧长公式:r l ||α= (α是角的弧度数)
扇形面积:2||2
121r lr S α===
3
、三角函数 (1)、定义:(如图) (2)y
r
y x r x x
r
x y r y ======ααααααcsc cot cos sec tan sin
4、同角三角函数基本关系式
(1)平方关系: (2)商数关系: (3)倒数关系:
1cos sin 22=+αα α
α
αcos sin tan = 1cot tan =αα αα22sec tan 1=+ α
α
αsin cos cot =
1csc sin =αα αα22csc cot 1=+ 1sec cos =αα
(4)同角三角函数的常见变形:(活用“1”) ①、αα22
cos 1sin
-=, αα2cos 1sin -±=;αα22sin 1cos -=, αα2sin 1cos -±=;
②θ
θθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,ααα
ααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-
③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=±
x
y
+ + _
_
O x
y
+
+
_
_ O
αtan
x
y
+ +
_
_
O
=r αsec
αsin
αtan αcot
csc
5、诱导公式:(奇变偶不变,符号看象限)
公式一: ααααααtan )360tan(cos )360cos(sin )360sin(=??+=??+=??+k k k
公式二: 公式三: 公式四: 公式五:
ααααα
αtan )180tan(cos )180cos(sin )180sin(-=-?-=-?=-? ααααα
αtan )180tan(cos )180cos(sin )180sin(=+?-=+?-=+? ααααααtan )tan(cos )cos(sin )sin(-=-=--=- α
αααααtan )360tan(cos )360cos(sin )360sin(-=-?=-?-=-?
补充:α
απααπααπ
cot )2
tan(sin )2cos(cos )2sin(
=-=-=- ααπααπα
απ
cot )2tan(sin )2cos(cos )2sin(
-=+-=+=+ ααπ
ααπααπcot )23tan(sin )2
3cos(cos )2
3sin(
=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(
-=+=+-=+
6、两角和与差的正弦、余弦、正切 7 .辅角公式 ???
? ??++++=+x b a b x b a a b a x
b x a cos sin cos sin 2
22222 )sin()sin cos cos (sin 2222???+?+=?+?+=x b a x x b a
(其中?称为辅助角,?的终边过点),(b a ,a
b =
?tan ) (多用于研究性质) 8、二倍角公式:(1)、α2S : αααcos sin 22sin = (2)、降次公式:(多用于研究性质) α2C : ααα2
2
sin cos 2cos -= ααα2sin 21
cos sin =
1cos 2sin 2122-=-=αα 2
12cos 2122cos 1sin 2
+-=-=ααα
α2T : α
αα2
tan 1tan 22tan -= 212cos 2122cos 1cos 2
+=+=ααα (3)、二倍角公式的常用变形:①、|sin |22cos 1αα=-, |cos |22cos 1αα=+;
②、
|sin |2cos 2121αα=-, |cos |2cos 2
121αα=+
③2
2sin 1cos sin 21cos sin 22
2
4
4
ααααα-=-=+; ααα2cos sin cos 4
4=-;
④半角:2cos 12
sin αα
-±
=,2cos 12cos αα+±=,α
ααcos 1cos 12tan +-±=αααα
cos 1sin sin cos 1+=
-=
9、三角函数的图象性质 (1)、函数的周期性:①、定义:对于函数f (x ),若存在一个非零常数T ,当x 取定义域内的每一个值时,都有:f (x +T )= f (x ),那么函数f (x )叫周期函数,非零常数T 叫这个函数的周期;
②、如果函数f (x )的所有周期中存在一个最小的正数,这个最小的正数叫f (x )的最小正周期。 (2)、函数的奇偶性:①、定义:对于函数f (x )的定义域内的任意一个x , 都有:f (-x )= - f (x ),则称f (x )是奇函数,f (-x )= f (x ),则称f (x )是偶函数
②、奇函数的图象关于原点对称,偶函数的图象关于y 轴对称; ③、奇函数,偶函数的定义域关于原点对称;
x y sin =图象的五个关键点:(0,0),(
2
,1),(π,0),(2,-1),(π2,0);
π
,0),(π,-1),(3π,0),(π2,1);
x y sin =的对称中心为(0,πk )
;对称轴是直线2
π
π+=k x ; )sin(?ω+=x A y 的周期ωπ
2=
T ;
x y cos =的对称中心为(0,2ππ+k );对称轴是直线πk x =; )cos(?ω+=x A y 的周期ω
π
2=T ; x y tan =的对称中心为点(0,πk )和点(0,2ππ+k ); )tan(?ω+=x A y 的周期ω
π
=T ; (4)、函数)0,0)(sin(>>+=ω?ωA x A y 的相关概念:
)sin(?ω+=x A y 的图象与x y sin =的关系:
①、振幅变换:x y sin = x A y sin =
②、周期变换:x y sin = x y ωsin =
③、相位变换:x y sin = )sin(?+=x y
④、平移变换:x A y ωsin = )sin(?ω+=x A y 常叙述成: ①、把x y sin =上的所有点向左(0>?时)或向右(0
平移|?|个单位得到)sin(?+=x y ; ②、再把)sin(?+=x y 的所有点的横坐标缩短(1>ω)或伸长(<01<ω)到原来的
ω
1
