汪荣鑫版数理统计 随机过程课后题标准答案打包下载

第一部分:数理统计习题解答第一章
1.解:
2. 解:子样平均数
子样方差
子样标准差
3. 解:因为
所以
所以
成立
因为
所以
成立
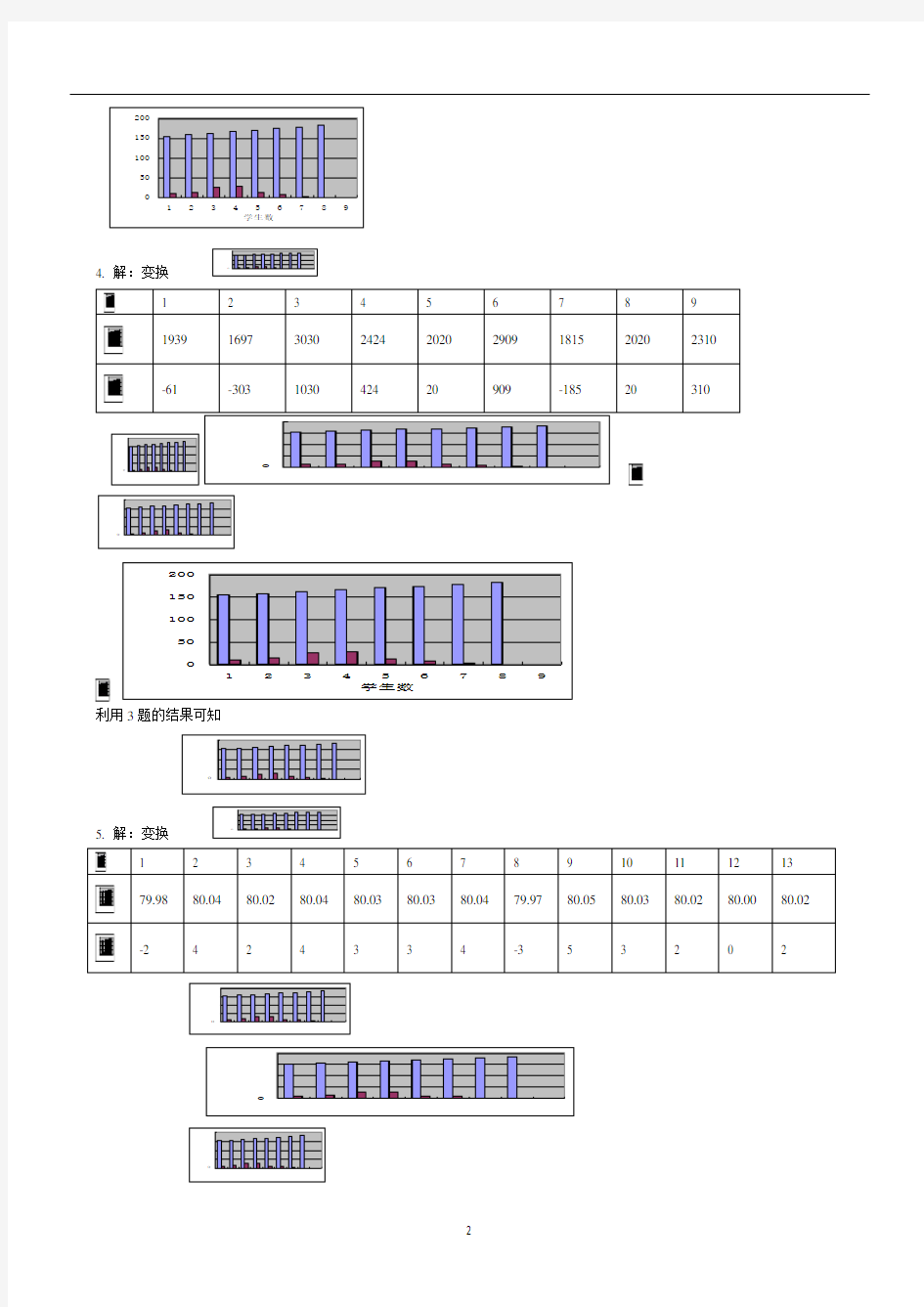
4. 解:变换
利用3题的结果可知
5. 解:变换
利用3题的结果可知
6.
7解:
8解:将子样值重新排列(由小到大)
-4,-2.1,-2.1,-0.1,-0.1,0,0,1.2,1.2,2.01,2.22,3.2,3.21
9解:
10.某射手进行20次独立、重复的射手,击中靶子的环数如下表所示:
解:
12. 解:
()
i
x P λ
i Ex λ
=
i Dx λ
=
1,2,,i n =???
112
211
1111
n n i i i i n n
i i i i n E X E x Ex n n n
n DX D x Dx n n
n n λ
λ
λλ
===========
=∑∑∑∑
13.解:
()
,i
x U a b
2i a b
Ex += ()2
12
i b a Dx -=
1,2,,i n =???
在此题中
()
1,1i
x U - 0
i Ex =
1
3i Dx =
1,2,,i n =???
11
2
11
110
11
1
3n n
i i i i n n
i i i i E X E x Ex n n DX D x Dx n n
n ==========
∑∑∑∑
14.解:因为
()2
,i
X N μσ
i X E
μ
σ
-=
1
i X D
μ
σ
-=
所以
()
0,1i X N μ
σ
-
1,2,,i n =???
由2χ分布定义可知
()
2
2
2
1
11
n
n
i
i
i i X Y X
μμσ
σ==-??
=
-= ??
?∑∑服从
2χ分布
所以
()
2Y
n χ
15. 解:因为
()
0,1i
X N
1,2,,i n =??? ()
123
0,3X X X N ++
0E
=
1=
所以
()
0,1N
()
2
21χ
同理
()
2
21χ
由于2
χ分布的可加性,故
()
22
2123Y χ=+
可知
1
3C =
16. 解:(1)因为
()20,i
X N σ
1,2,,i n =???
()
0,1i
X N σ
所以
()
2
2121n
i i X Y n χσσ=??= ?
??
∑
(){}11122Y Y
y F y P Y y P σ
σ??=≤=≤??
??
()2
20
y
f x dx
σχ=
?
()()211'22
1
Y Y y f y F y f χσσ
??==? ???
因为
()2122202200n x n x e x n f x x χ--??>?
??
=?Γ ????
?≥?
所以
()21122202200n y n n
Y y e y n f y y σσ--??>?
??=?Γ ????
?≤?
(2) 因为
()20,i X N σ
1,2,,i n =???
()
0,1i
X N σ
所以
()
2
2221n
i i X nY n χσσ=??= ?
??
∑
(){}()2
2222220ny
Y nY ny F y P Y y P f x dx
σχσσ??
=≤=≤=?????
()()222'22
Y Y ny n
f y F y f χσσ
??== ???
故 ()221222202200n n
ny n n Y n y e y n f y y σσ--??>?
??
=?Γ ?
???
?≤?
(3)因为
()20,i
X N σ
1,2,,i n =???
()
1
0,1n
i N =
所以
()
2
23
1
1n
i Y n χσ
=?= ?
(){}()()2
2333210
y
n Y Y F y P Y y P y f x dx
n σ
χσ??
=≤=≤=?????
()()()233'22
11
Y Y y f y F y f n n χσσ
??== ???
()(
)22
1000x x f x x χ-?>=≤?
故 (
)2
32000
y
n Y y f y y σ-?>=≤?
(4)因为
()
20,i
X N σ
1,2,,i n =???
所以
(
)
()
1
2
242
10,11n
i n i N Y χσ
==?= ?
(){}()()()()()2
242244
42210'22
11
y
Y Y Y y F y P Y y P f x dx
y f y F y f σχχχσ
σσσ
??=≤=≤=??????== ????
故
(
)242000y Y y f y y σ-?>=≤?
17.解:因为 ()
X
t n
存在相互独立的U ,V
()
0,1U
N
()
2V
n χ
使
X =
()
2
21U χ
则
2
21
U X V n
=
由定义可知
()
2
1,F n χ
18解:因为
()20,i
X N σ
1,2,,i n =???
()
1
0,1n
i N =
()
2
21n m
i i n X m χσ+=+?? ???
∑
所以
()
1n
n
i
X Y t m =
=
(2)因为
()
0,1i
X N σ
1,2,,i n m =???+
()
()
2
212
21n
i i n m
i i n X n X m χσχσ=+=+?? ???
?? ???
∑∑
所以
()
2
211
22211,n
i n i i
i n m n m
i i
i n i n X m X n Y F n m X n X m σσ==++=+=+??
???==?? ???
∑∑∑∑
19.解:用公式计算
(
)2
0.010.01
9090χ=
查表得
0.01 2.33
U =
代入上式计算可得 ()20.01909031.26121.26
χ=+=
20.解:因为
()
2X
n χ
2E n χ= 22D n χ=
由2
χ分布的性质3可知
()
0,1N
{
}P X c P ≤=≤
2
2lim t n P dt -→∞-∞
≤==Φ
故 {
}P X c ≤≈Φ
第 二 章 1.
,0
()0,0()()1
()
1
1
1
x x x x x
e x
f x x E x f x xdx xe dx
xe e d x e x
λλλλλλλλλ
λ
λ
λ
-+∞
+∞
--∞+∞
+∞--+∞-?≥=?
?==-+=-=
=?
?
?
令
从而有 1x λ∧
=
2.
()1
1
1
1
2
1).()(1)
(1)1
1
11k k x x E x k p p p k p p
p
p ∞
∞
--===-=-==
??--??
∑∑
令1
p =X
2).其似然函数为1`
1
1
()(1)
(1)n
i x i i n
X n
n
i L P P p p p -=-=∑=-=-∏
解之得
1
1
n
i
i n
p X
X
∧
==
=
∑
3. 解:因为总体X服从U(a ,b )所以
()21
22!
2!!
()12n
i i a b n E X r n r X X X X a b S X b X =∧
∧
+=--?=???-?=???=-???=+?∑2
2
2(a-b )() D (X )=
12令E (X )= D (X )=S ,
1S =
n a+b
2
()a
4. 解:(1)设
12,,
n
x x x 为样本观察值则似然函数为:
11
1
()(),01,1,2,,ln ()ln ln ln ln 0
n n
i i i n
i
i i n
i
i L x x i n
L n x d L n
x
d θθθθθθθθ
-====<<==+=+
=∏∑∑(-1)
解之得:
1
1
ln ln n
i
i n
i
i n
x
n
x
θθ=∧
==-
==
∑∑
(2)母体X 的期望
1
()()1E x xf x dx x dx θθθθ+∞
-∞
===
+?
?
而样本均值为:
5.。解:其似然函数为:
1
1
11
1
11()2(2)1
ln ()ln(2)1
0n
i
i
i x n
x n
i n i i n
i
i L e e L n x x σσσσ
σσσσ
σσ
=-
-==∧
=∑
=?=?=--=
∏∑=∑令
得:
(2)由于
00
1
1
2221
1
1
()(
)()x x x x
n
n
i i i i x x E e dx e dx x e e
dx E E x E x n n
n
n
σσσ
σ
σ
σσ
σσσ+∞
----
+∞
+∞+∞
-∞
∧
===
==-+
===
=
?=?
??
∑
∑
所以
11n i
i x n σ∧
==∑ 为σ的无偏估计量。 6. 解:其似然函数为:
(1)(1)()()(1)!
(1)!11k k n n k x n x i k i L x e x e
i i k k i i βββββ----∏==∏--==
ln ()ln (1)ln()11n n
L nk k X X i i
i i βββ=+--∑∑==
1
ln ()0
n
i
i d L nk
d X
βββ
==-
=∑
解得
1
n
i
i nk
k
X
X
β∧
==
=
∑1
(),0,
f x x ββ=≤≤
7.解:由题意知:均匀分布的母体平均数
22
β
βμ=
-=
,
方差
1212)0(2
22
ββλ=
-=
用极大似然估计法求
β得极大似然估计量
似然函数:
∏
==n
i n
L 1
1
)(θβ
β
≤≤≤≤≤n
i i i i x x 1)
(max min 0
选取
β使L 达到最大
取
n
i i
x ≤≤∧
=1max β
由以上结论当抽得容量为6的子样数值1.3,0.6,1.7,2.2,0.3,1.1,时
2.2=∧
β即
,
1.12
==
∧
∧
β
μ
4033.0122
.22.212
2
2
≈?=
=
∧
βσ
8. 解:取子样值为
)(),,,(21θ≥i n x x x x
则似然函数为:
∏=--=n
i x i e L 1)
()(θθ
θ
≥i x
∑∑==+-=--=n
i n
i i i n x x L 1
1
)()(ln θ
θθ
要使似然函数最大,则需θ取
)
,,,min(21n x x x
即
∧
θ=),,min(21n x x x
9. 解:取子样值)
0)(,,(2,1>i n x x x x
则其似然函数
∑===-=-∏n
i i
i
x n
n
i x e
e
L 1
1
)(λ
λλλλ
∑=-=n
i i
x n L 1
ln )(ln λλλ
∑=-=n
i i
x n
d L 1
)(ln λλλ
x
x
n
n
i i
1
1
=
=
∑=∧
λ
由题中数据可知
20)6525554545703510025150152455365(10001
=?+?+?+?+?+?+?=
x
则
05.0201
==
∧
λ
10. 解:(1)由题中子样值及题意知:
极差7.45.12.6=-=R 查表2-1得4299.01
5
=d 故0205.27.44299.0=?=∧
λ
(2)平均极差115.0=R ,查表知3249.01
10
=d
0455.0115.03249.0=?=∧
λ
解:设∧
u 为其母体平均数的无偏估计,则应有
x =∧
μ
又因
4)26261034018(601
=?+?+?+?=
x
即知
4=∧
μ
12. 解:
)1,(~μN X
μ
=∴)(i x E ,
1
)(=i x D ,
)2,1(=i 则
μμ=+=
∧
21132
31)(EX EX E
μμ=+=
∧
21243
41)(EX EX E
μ
μ=+=∧21321
21)(EX EX E 所以三个估计量
321,,∧
∧∧μμμ均为μ的无偏估计
9591949194)3132()(2121=
+=+=+=∧
DX DX X X D D μ
同理可得
85)(2=∧
μD ,21)(2=
∧μD 可知
3∧μ的方差最小也亦∧
2
μ最有效。
13解:
)(~λP X λλ==∴)(,)(X D X E
])(11[)(12
2
*∑=--=n i i X X n E S E )]()([1121
2X nE X E n n
i i
--=∑=
])()([11122∑=+-+-=n
i n n n λλλλλλλ=--=)(11n n 即
2
*S 是λ的无偏估计
又因为λ
====∑∑∑===n
i i n
i i n i i EX n X E n X n E X E 1
111)(1)1()(
即
X
也是λ的无偏估计。
又]1,0[∈?α
λλλαλααα=-+=-+=-+)1()()1()())1((2
*2
*S E X E S X a E
因此
2
*
)1(S X αα-+也是λ的无偏估计
14.解:由题意:
),(~2
σμN X
因为
]
)(()([)()(2111
1212
i i n i i i i i X X E X X D C X X E C E -+-=-=+-=++∧
∑∑λ
2
11
211
1)1(22]0)()([λλ-==++=∑∑-=-=+n C C X D X D C n i n i i i
要使
2
2
)(λ
λ=∧E 只需
)1(21+=
n C 所以当)
1(21
-=
n C 时2
∧λ为2
λ的无偏估计。
15.证明: 参数θ的无偏估计量为∧
θ,∧
θD 依赖于子样容量n 则
,0>?ε由切比雪夫不等式
0lim =∧
∞→θD n 故有
1lim =??????<-∧∞
→εθθp n 即证∧
θ为θ的相合估计量。 16证明:设X 服从
),(p N B ,则分布律为
k
k k
N P P k X P C )1()(-==
),2,1(N k =
这时NP X E =)( )1()(P NP X D -=
2
222)1()(P N P NP EX DX EX +-=+= 例4中
N
X
p -
∧
=
所以
P N NP
N X E P E ===
-
∧
)((无偏)
Nn P P n
N P NP N X D P D )
1()1(2
2-=-==
-
∧
罗—克拉美下界满足
∑=----??=n
k P N K K
N P N K K N R P P P P Ln p
n I C C 02)1(])1([1
∑=----++??=N
K K N K K
N K N P P P Ln P N KLnP Ln P
n C C 02)1())]1()(([
∑=-----=N
K K N K
K N P P P P N P K n C 02)1(]1[ ])1(2)1(22[2
22222P EX NEX N P P EX NEX P EX n -+-+---=
2
2
2222222222)1()1(2)1()1(2)1([P P N P NP P N N P P N P NP P N P P N P NP n -+-+-+
-----+-=
)1(]111[
P P nN P P nN -=
-+= 所以∧=-=P D nN P P I R )
1(即∧
p 为优效估计
17. 解:设总体X 的密度函数
2
22)(21)(σμσ
π--
=
x e
x f
似然函数为
∏
=---
-∑===n
i x n
x n
i i i e
e
L 1
2)(2
2
2)(2
2
1
2
2
2
)2(21)(σμσμπσσ
πσ
2
1
2
222)(222)(σ
μσπσ∑=--
--=n
i i
x
Ln n
Ln n LnL
2)(24
1
2
2
2=-+-=∑=σμσσn
i i
x
n
d dLnL
∑=-=n
i i x n 1
2
2
)(1μσ
因为?+∞
∞-??dx x f x Lnf )())((2
2σ=
?∞+∞---
--dx
e
x x 2
22)(2242
21]212)([σμσ
πσσμ
=]2)()([41
4
2248
σσμμσ+---X E X E =
4
2σn
故2
σ的罗—克拉美下界
42σn I R =
又因
∑=∧-=n i i X n E E 12
2
))(1(μσ∑=-=n
i i X E n 12)
)((1μ2σ= 且
∑=-=n
i i X n D D 122
))(1()(μσ4
2σn = 所以2
∧σ
是2
∧σ
的无偏估计量且
)(2
∧=σD I R 故2
∧σ
是2
∧σ
的优效估计
18. 解:由题意:n=100,可以认为此为大子样,
所以
n
S X U μ
-=
近似服从
)1,0(N
α
α-=1}{2
u U P
得置信区间为n
s u x 2
(α
-
)
2
n
s u x α
+
已知95.01=-α
s=40 x =1000 查表知
96
.12
=αu 代入计算得
所求置信区间为(992.16 1007.84)
19.解:(1)已知cm 01.0=σ
则由)
1,0(~N n
X U σ
μ
-=
α
α-=<1}{2
u U P
解之得置信区间
n
u X σ
α
2
(-
)
2
n
u X σ
α
+
将n=16
X
=2.125
645
.105.02
==u u α
01.0=σ
代入计算得置信区间(2.1209 2.1291)
(2)σ未知
)1(~--=
n t n S X T μ
α
α-=<1}{2
t T P
解得置信区间为
2
(α
t n
s X -
)
2
αt n
s X +
将n=16
753
.1)15()15(05.02
==t t α
00029.02=S 代入计算得
置信区间为(2.1175 2.1325)。
20.。解:用T 估计法
)1(~--=
*
n t n S
X T μ
α
α-=-<1)}1({2
n t T P
解之得置信区间2
(α
t n
S X *-
)
2
*αt n
S X +
将6720
=X
220=*S n=10 查表2622
.2)9(025.0=t
代入得置信区间为(6562.618 6877.382)。
21.解:因n=60属于大样本且是来自(0—1)分布的总体,故由中心极限定理知 )
1()
1(1
p np np X n p np np
X
n
i i
--=
--∑=近似服
从
)1,0(N 即
α
α-=<--1})
1()({
2
u p np P X n p
解得置信区间为
2
)
1((α
u n p p X --
))
1(2
αu n p p X -+
本题中将n U n
代替上式中的X 由题设条件知25
.0=n U n
055.0)()1(2=-=-n U n U n p p n n 查表知96.1025.0==U U n
代入计算的所求置信区间为(0.1404 0.3596)
22. 解:2
σ未知 故
)
1,0(~N n
X U σ
μ
-=
由
α
α-<<1}{2
u U P 解得
置信区间为
2(ασu n X -
)2ασ
u n X +
区间长度为
2
2α
σ
u n
于是
L
u n
≤2
2ασ
计算得
2
2
224α
σU L n ≥ 即为所求
23.解:μ未知,用2χ估计法
)
1(~)1(22
2
2
--=
n S n χσχ
α
χχχαα-=-<-<--
1)}1()1()1({22
2221n n n P
解得σ的置信区间为2
2
2
)1((
αχS n -
)
)1(22
12
α
χ--S n
(1)当n=10,*S =5.1时 查表)9(2005.0χ=23.59 )9(2995.0χ=1.73
代入计算得σ的置信区间为(3.150 11.616) (2)当n=46,*
S =14时 查表
)
45(2005.0χ=73.166
)
45(2995.0χ24.311
代入计算可得σ的置信区间为(10.979 19.047) 24.解:(1)先求
μ的置信区间 由于σ
未知
)1(~--=
n t n S X T μ
α
α-=<1}{2
t T P
得置信区间为
2
(α
t n
S X -
)
2
αt n
S X +
经计算2203.012
.5==S X 查表093
.2)19(025.0=t n=20
代入计算得置信区间为(5.1069 5.3131)
(2)
μ未知 用统计量
)
1(~)1(22
2
2
--=
n S n χσχ
α
χχχαα-=<<-1}{2
2
222
1P
得σ的置信区间为22
2)1((
α
χS n -
)
)1(22
12
αχ
-
-S n
查表
)
19(2025.0χ=32.85
)
19(2975.0χ=8.91
代入计算得σ的置信区间为(0.1675 0.3217) 25.解:因
1
+n X 与
n
X X X ,,21相互独立,所以
1
+n X 与
X
相互独立,故
)
)11(,0(~21σn N X X n +-+
又因
)
1(~22
2
-n nS χσ 且与
X
X n -+1相互独立,有T 分布的定义知
)1(~1
1
)1(1
12
21-+--=-+-++n t n n S
X X n nS n n X X n n σσ
26. 解:因)
,(~21σμN X i
m i ,2,1= ),(~2
2σμN Y j n j ,2,1=
所以)
,
0(~)(2
21m
N X σαμα-,
)
,
0(~)(2
22n
N Y σβμβ-
由于
X
与Y 相互独立,则
)]
(,0[~)()(2
2
21n
m
N Y X βαμβμα+
-+-
即
)
1,0(~)
()(2
2
21N n
m
Y X σ
β
α
μβμα+
-+-又因
)
1(~22
2-m ms x
χσ
)
1(~22
2-n ns y
χσ
则
)
2(~22
22
2-++
n m ns ms y
x
χσσ
构造t 分布
n m
Y X 2
2
21)
()(β
α
σ
μβμα+
-+-=
)
2(~2)
()(2
2
2221-++
-++-+-n m t n
m
n m ns
ms Y X y
x
β
α
μβμα
27. 证明:因抽取n>45为大子样
)
1(~)1(22
2
*
2--=
n s n χσχ
由2χ分布的性质3知
)
1(2)
1(2---=
n n U χ近似服从正态分布
)1,0(N
所以
α
α-=≤1}{2u U P
得
2
2)
1(2)
1(αχu
n n ≤--- 或
2
2
2
2)
1(2)
1()1(αασ
u n n s n u ≤----≤
-
可得2
σ的置信区间为
???????????
?---+22
2
2121,121ααu n s u n s 28. 解: 因2
2221σσσ==未知,故用T 统计量
