物理竞赛中数学知识

物理竞赛中的数学知识

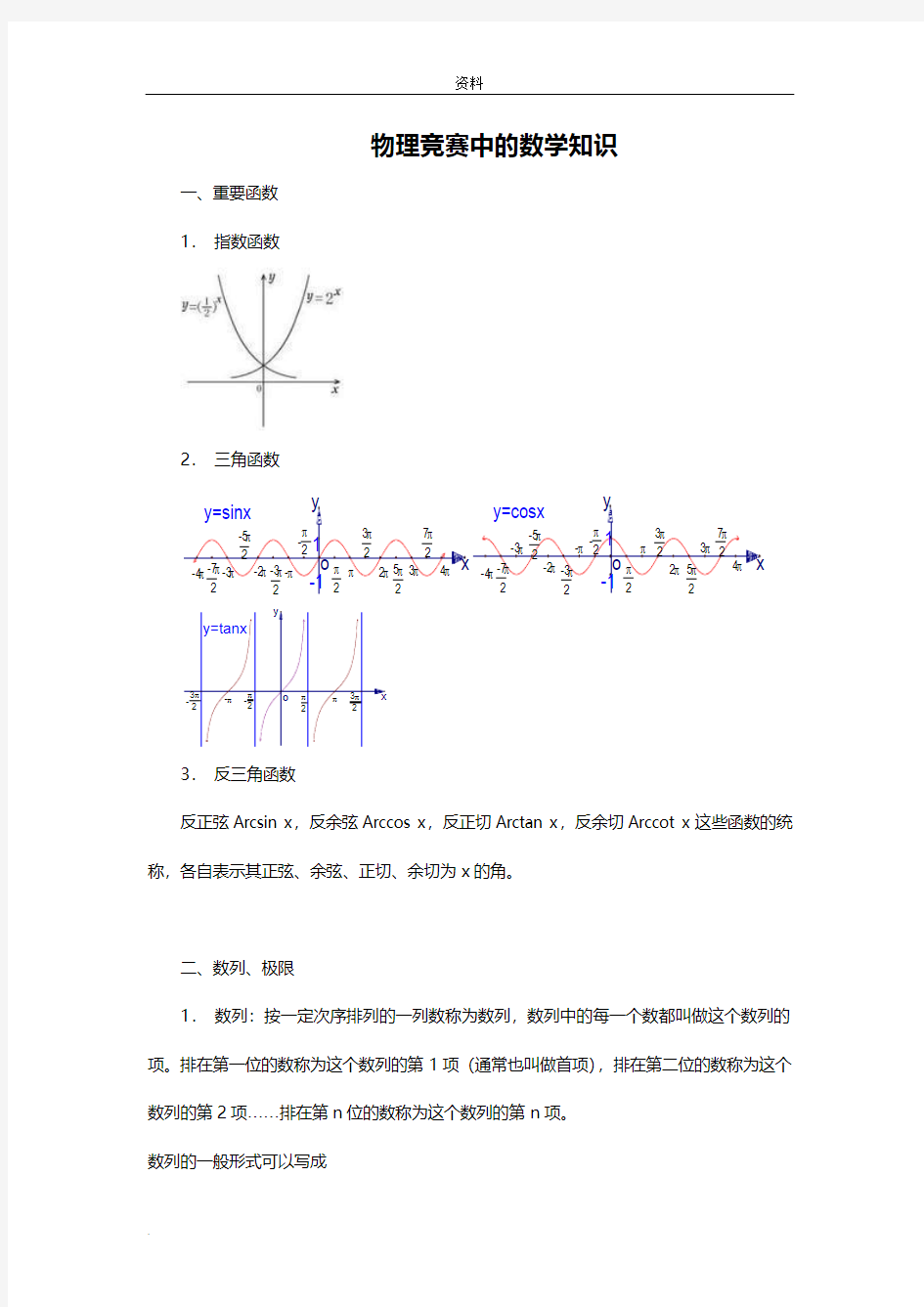
一、重要函数

1．指数函数

2．三角函数

3．反三角函数

反正弦Arcsin x，反余弦Arccos x，反正切Arctan x，反余切Arccot x这些函数的统称，各自表示其正弦、余弦、正切、余切为x的角。

二、数列、极限

1．数列：按一定次序排列的一列数称为数列，数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项。

数列的一般形式可以写成

a 1，a 2，a 3，…，a n ，a （n+1），… 简记为｛an ｝，

通项公式：数列的第N 项a n 与项的序数n 之间的关系可以用一个公式表示，这个公式就叫做这个数列的通项公式。

2．等差数列：一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示。通项公式a n =a 1+(n-1)d ，前n 项和11(1)

n n a a n n S n na d +-=

=+ 等比数列：一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同

一个常数，这个数列就叫做等比数列。这个常数叫做等比数列的公比，公比通常用字母q

表示。通项公式a n =a 1q (n-1)，前n 项和11

(1)(1)11n

n n a a q a q S q q q

--=

=≠-- 所有项和1

(1)1n a S q q

=<-

3．求和符号

4．数列的极限：

设数列{}n a ,当项数n 无限增大时,若通项n a 无限接近某个常数A ,则称数列{}n a 收敛于

A ,或称A 为数列{}n a 的极限,记作A a n n =∞

→lim

否则称数列{}n a 发散或n n a ∞

→lim 不存在.

三、函数的极限：在自变量x 的某变化过程中，对应的函数值f (x )无限接近于常数A ，则称常数A 是函数f (x )当自变量x 在该变化过程中的极限。

设f (x )在x>a (a >0)有定义,对任意ε>0,总存在X >0,当x>X 时，恒有| f (x )-A |<ε，则称常数A 是函数f (x )当x →+∞时的极限。记为+∞

→x lim f (x )=A ，或f (x ) → A (x →+∞)。

运算法则

lim x x →[f (x )± g (x )]=0

lim x x →f (x ) ±0

lim x x →g (x )

lim x x →[f (x ) ? g (x )]=0

lim x x →f (x ) ?0

lim x x →g (x )

)

(lim )(lim )()(lim 0

0x g x f x g x f x x x

x x x →→→=，其中0lim x x →g (x )≠ 0.

四、无穷小量与无穷大量

1．若0)(lim 0

=→x f x x ，则称)(x f 是0x x →时的无穷小量。

（若,)(lim 0

∞=→x g x x 则称)(x f 是0x x →时的无穷大量）。

或：若0

lim x x →α(x )=0 ,则称α(x )当x → x 0时为无穷小。

在自变量某变化过程中，|f (x )|无限增大，则称f (x )在自变量该变化过程中为无穷大。记为 lim ().f x =∞

2．无穷小量与无穷大量的关系

无穷小量的倒数是无穷大量；无穷大量的倒数是无穷小量。 3．无穷小量的运算性质

（i ）有限个无穷小量的代数和仍为无穷小量。（ii ）无穷小量乘有界变量仍为无穷小量。（iii ）有限个无穷小量的乘积仍为无穷小量。 4．无穷小的比较

定义：设0

lim →x α (x )=0，0

lim →x β (x )=0，

1)若)

()

(lim

0x x x αβ→=0，则称当x → x 0时β (x )是比α (x )高阶无穷小。

2)若)

()

(lim

0x x x αβ→=∞，则称当x → x 0时β (x )是比α (x )低阶无穷小。

3)若)

()

(lim

0x x x αβ→=C (C ≠0)，则称当x → x 0时β (x )与α (x )是同阶无穷小，

4)若)

()

(lim

0x x x αβ→=1,则称当x → x 0时β (x )与α (x )是等价无穷小。

5．常用的等价无穷小为：

当x →0时： sin x ~x ，tan x ~x ，arcsin x ~x ，arctan x ~x ，1-cos x ~22

1x ，

11-+n

x ~x n 1。等价无穷小可代换

五、二项式定理

1．阶乘： n!=1×2×3×……×n

2．组合数：从m 个不同元素中取出n （n ≤m ）个元素的所有组合的个数，叫做从m 个不同元素中取出n 个元素的组合数

3．二项式定理

即

六、常用三角函数公式

sin （π＋α）＝－sin α cos （π＋α）＝－cos α tan （π＋α）＝tan α sin （π/2＋α）＝cos α cos （π/2＋α）＝—sin α tan （π/2＋α）＝－cot α

sin()sin cos cos sin A B A B A B +=+ s i n ()s i n c o s c o s s i A B A B A B -=- cos()cos cos sin sin A B A B A B +=- c o s ()c o s

c o s

s i n s i

A B A B A B -=+ sin 22sin cos A A A = 2222cos 2cos sin 12sin 2cos 1A A A A A =-=-=- 2

2tan tan 21tan A

A A

sin

2A = cos 2A = s i n t a n 21c o s

A A A ==+ 和差化积公式

sin sin 2sin

cos 22a b a b a b +-+=? sin sin 2cos sin

22a b a b

a b +--=? cos cos 2cos cos 22a b a b a b +-+=? cos cos 2sin sin

a b a b

a b +--=-? ()

sin tan tan cos cos a b a b a b

++=?

积化和差公式

()()1sin sin cos cos 2a b a b a b =-+--???? ()()1

cos cos cos cos 2a b a b a b =++-????

()()1s i n c o s s i n s i n 2a b a b a b =++-???? ()()1

c o s s i n s i n s i n 2

a b a b a b =+--????

万能公式

22tan

2sin 1tan 2

a a

+ 2

1tan 2cos 1tan 2a a a -=+ 22t a n

2t a n 1t a n 2

a a =-

典型物理问题

数列极限等应用

1．蚂蚁离开巢穴沿直线爬行，它的速度与到蚁巢中心的距离成反比，当蚂蚁爬到距巢中心距离L 1=1m 的A 点处时，速度是V 1=2cm/s 。试问蚂蚁继续由A 点到距巢中心L 2=2m 的B 点需要多长时间？

2．

常见近似处理

1．人在岸上以v 0速度匀速运动，如图位置时，船的速度是多少？

2．如图所示，顶杆AB 可在竖直滑槽K 内滑动，其下端由凹轮M 推动，凸轮绕O 轴以匀角速度ω转动.在图示的瞬时，OA=r ，凸轮轮缘与A 接触，法线n 与OA 之间的夹角为α，试求此瞬时顶杆AB 的速度.(第十一届全国中学生物理竞赛预赛试题)

3．三个芭蕾舞演员同时从边长为L的正三角形顶点A,B,C出发，速率都是v，运动方向始终保持着A朝着B,B朝着C,C朝着A。经过多少时间三人相遇？每人经过多少路程？

4．如图所示，半径为R2的匀质圆柱体置于水平放置的、半径为R1的圆柱上，母线互相垂直，设两圆柱间动摩擦因数足够大，不会发生相对滑动，试问稳定平衡时，R1与R2应满足什么条件?

5.一只狐狸以不变的速度1υ沿着直线AB 逃跑，一只猎犬以不变的速率2υ追击，其运动方向始终对准狐狸.某时刻狐狸在F 处，猎犬在D 处，FD ⊥AB ，且FD=L ，如图14—1所示，求猎犬的加速度的大小.

解析：猎犬的运动方向始终对准狐狸且速度大小不变，故猎犬

做匀速率曲线运动，根据向心加速度r r

a ,22

υ=

为猎犬所在处的曲

率半径，因为r 不断变化，故猎犬的加速度的大小、方向都在不断变化，题目要求猎犬在D 处的加速度大小，由于2υ大小不变，如果求出D 点的曲率半径，此时猎犬的加速度大小也就求得了.

猎犬做匀速率曲线运动，其加速度的大小和方向都在不断改变.在所求时刻开始的一段

很短的时间t ?内，猎犬运动的轨迹可近似看做是一段圆弧，设其半径为R ，则加速度 =

a R

其方向与速度方向垂直，如图14—1—甲所示.在t ?时间内，设狐狸与猎犬分别到达

D F ''与，猎犬的速度方向转过的角度为=α2υt ?/R

而狐狸跑过的距离是：1υt ?≈L α 因而2υt ?/R ≈1υt ?/L ，R=L 2υ/1υ

所以猎犬的加速度大小为=

a R

υ=1υ2υ/L

6．如图所示，半径为R ，质量为m 的圆形绳圈，以角速率ω绕中心轴O 在光滑水平面上匀速转动时，绳中的张力为多大？

解析取绳上一小段来研究，当此段弧长对应的圆心角θ?很小时，有近似关系式.sin θθ?≈?

若取绳圈上很短的一小段绳AB=L ?为研究对象，设这段绳所对应

的圆心角为θ?，这段绳两端所受的张力分别为A T 和B T （方向见图14

—3—甲），因为绳圈匀速转动，无切向加速度，所以A T 和B T 的大小相等，均等于T . A T 和

B T 在半径方向上的合力提供这一段绳做匀速圆周运动的向心力，设这段绳子的质量为m ?，

根据牛顿第二定律有：R m T 22sin 2ωθ?=?；

因为L ?段很短，它所对应的圆心角θ?很小所以22sin θθ?=?

将此近似关系和π

πθ22?=

??=?m R m R m 代入上式得绳中的张力为π

ω22R

m T =

7．在某铅垂面上有一固定的光滑直角三角形细管轨道ABC ，光滑小球从顶点A 处沿斜边轨道自静止出发自由地滑到端点C 处所需时间，恰好等于小球从顶点A 处自静止出发自由地经两直角边轨道滑到端点C 处所需的时间.这里假设铅垂轨道AB 与水平轨道BC 的交接处B 有极小

的圆弧，可确保小球无碰撞的拐弯，且拐弯时间可忽略不计.

在此直角三角形范围内可构建一系列如图14—4中虚线所示的光滑轨道，每一轨道是

由若干铅垂线轨道与水平轨道交接而成，交接处都有极小圆弧（作用同上），轨道均从A 点出发到C 点终止，且不越出该直角三角形的边界，试求小球在各条轨道中，由静止出发自由地从A 点滑行到C 点所经时间的上限与下限之比值.

解析直角三角形AB 、BC 、CA 三边的长分别记为

1l 、2l 、3l ，如图14—4—甲所示，小球从A 到B 的时间记为1T ，再从B 到C 的时间为2T ，而从A 直接沿斜边到C

所经历的时间记为3T ，由题意知321T T T =+，可得1l ：2l ：3l =3：4：5，由此能得

1T 与2T 的关系. 因为2112112

T gT l gT l ==

所以

1212T T l l = 因为1l ：2l =3：4，所以 123

2T T =

小球在图14—4—乙中每一虚线所示的轨道中，经各垂直线段所需时间之和为11T t =，

经各水平段所需时间之和记为2t ，则从A 到C 所经时间总和为21t T t +=，最短的2t 对应t 的下限min t ，最长的2t 对应t 的上限.m ax t

小球在各水平段内的运动分别为匀速运动，同一水平段路程放在低处运动速度大，所需

时间短，因此，所有水平段均处在最低位置（即与BC 重合）时2t 最短，其值即为2T ，故

min t =.3

5121T T T =+

2t 的上限显然对应各水平段处在各自可达到的最高位置，实现它的方案是垂直段每下降

小量1l ?，便接一段水平小量2l ?，这两个小量之间恒有αcot 12l l ?=?，角α即为∠ACB ，水平段到达斜边边界后，再下降一小量并接一相应的水平量，如此继续下去，构成如图所示

的微齿形轨道，由于1l ?、2l ?均为小量，小球在其中的运动可处理为匀速率运动，分别所经的时间小量)(1i t ?与)(2i t ?之间有如下关联：

αcot )()(1

12=??=??l l i t i t

于是作为)(2i t ?之和的2t 上限与作为)(1i t ?之和的1T 之比也为.cot α故2t 的上限必为

1T αcot ，即得：.3

cot 111max T T T t =+=α

这样:max t min t =7:5

求导与微分

一、导数的概念

1．导数定义

设y=f(x)在x 0的某邻域内有定义,在该邻域内给自变量一个改变量x ?,函数值有一相应改变量)()(00x f x x f y -?+=?,若极限

x x f x x f x y x x ?-?+=??→?→?)

()(lim

lim

0000 存在,则称此极限值为函数y=f(x)在x 0点的导数,此时称y=f(x)在x 0点可导,用

???

==='

'00

(,,)(x x dx x df x x dyx dy

x x y x f 或

或

表示.

若)(x f y =在集合D 内处处可导（这时称f(x)在D 内可导）,则对任意D x ∈0,相应的导数)(0x f '将随0x 的变化而变化,因此它是x 的函数,称其为y=f(x)的导函数,记作

?''dx x df dx

dy y x f )(,,)(或或

或

. 2．导数的几何意义

若函数f(x)在点x 0处可导,则)(0x f '就是曲线y=f(x)在点（x 0,y 0）处切线的斜率,此时切线方程为))((000x x x f y y -'=-.

当)(0x f '=0,曲线y=f(x)在点（x 0,y 0）处的切线平行于x 轴,切线方程为)(00x f y y ==. 若f(x)在点x 0处连续,又当0x x →时∞→')(x f ,此时曲线y=f(x)在点（x 0,y 0）处的切线垂直于x 轴,切线方程为x=x 0.

1．几个基本初等函数的导数 ⑴()0c '= ⑵1

x x

μμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=-

2．导数的四则运算（1）)(])([x u c x u c '?='?；（2）)()(])()([x v x u x v x u '+'='±；

（3）)()()()()]()([x v x u x v x u x v x u '?+'?'=?；

（4）)()

()()()()()(2

x v x v x u x v x u x v x u '-'='

????

二、微分

1．微分的概念

设)(x f y =在0x 的某邻域内有定义,若在其中给0x 一改变量x ?,相应的函数值的改变量y ?可以表示为

).0()

(0)()(00→??+?=-?+=?x x x A x f x x f y

其中A 与x ?无关,则称)(x f 在0x 点可微,且称A x ?为)(x f 在0x 点的微分,记为

x A x x df

x x dy

?====

x A ?是函数改变量y ?的线性主部.

)(x f y =在0x 可微的充要条件是)(x f 在0x 可导,且)(00

x x f x x dy

?'==.当

x x f =)(时,可得x dx ?=,因此

.)(,)(00

dx x f dy dx x f x x dy

'='==

由此可以看出,微分的计算完全可以借助导数的计算来完成.

（2）微分的几何意义当x 由0x 变到x x ?+0时,函数纵坐标的改变量为y ?,此时过0

x 点的切线的纵坐标的改变量为dy.如图2-1所示.

当dy y ?时,切线在曲线上方,曲线为凸弧. 2．微分运算法则设)(),(x v x u 可微,则

)

()

()()()()()().()()()()]()([).()()]()([.

0)(),())((2x v x dv x u x du x v x v x u d

x du x v x dv x u x v x u d x du x du x v x u d c d x cdu x cu d -=+=?±=±==

三、不定积分

1．不定积分概念

【定义】(原函数) 若对区间I 上的每一点x ,都有

,)()()()(dx x f x dF x f x F =='或

则称F （x ）是函数f(x)在该区间上的一个原函数.

原函数的特性若函数f(x)有一个原函数F(x ),则它就有无穷多个原函数,且这无穷多个原函数可表示为F （x ）+C 的形式,其中C 是任意常数.

【定义】(不定积分) 函数f(x)的原函数的全体称为f(x)的不定积分,记作

?dx x f )(.若

F(x)是f(x)的一个原函数,则

?+=)()()(是任意常数C C

x F dx x f

2．不定积分的性质

（1）积分运算与微分运算互为逆运算.

()()????+=+='==.

)()()()(,

)()()()(C x F x dF C x F dx x F dx x f dx x f d x f dx x f dx

d 或或

（2）??

≠=)0()()(k dx

x f k dx x kf 常数

（3）???±=

±.)()()]()([dx x g dx x f dx x g x f

3．基本积分公式

kdx kx c =+? 1

1x x dx c μμ

μ+=++?

c o s s i n x

d x x c =+? sin cos xdx x c =-+?

四、定积分

【定义】(定积分) 函数)(x f 在区间[a,b ]上的定积分定义为

∑?=→??==n

i i

x b

f dx x f I 1

)(lim

)(ξ，

【定理】(牛顿-莱布尼茨公式) 若函数)(x f 在区间[a,b ]上连续，)(x F 是)(x f 在[a,b ]上的一个原函数，则

)()()()(a F b F a

x F dx x f b

-==?

上述公式也称为微积分基本定理,是计算定积分的基本公式.

常见应用

1．一石砌堤，堤身在基石上，高为h，宽为b，如图所示。堤前水深等于堤高h，谁和堤身的单位体积重量分别为q和γ，问欲防止堤身绕A点翻倒，比值b/h应等于多少？

2．一个半径为四分之一的光滑球面置于水平桌面上．球面上有一条光滑均匀的匀质铁链，一端固定于球面顶点A，另一段恰好与桌面不接触，且单位长度铁链的质量为p，求铁链A 端所受到拉力以及铁连所受球面的支持力．

3．质量为m的均匀橡皮圈处于自然状态下的半径为r1，弹性系数为k。现将它保持水平套在半径为r2的竖直圆柱上（r2＞r1），套上后橡皮圈的质量分布仍是均匀的，橡皮圈与柱面之间的静摩擦因数为μ。现在圆柱体绕竖直轴转动起来，如图所示：问要保持橡皮圈不滑下，圆柱转动的角速度ω不能超过多少？

常用数学知识汇总

一、三角函数公式 1.两角和公式

sin()sin cos cos sin A B A B A B +=+ s i n ()s i n c o s c o s s i A B A B A B -=- cos()cos cos sin sin A B A B A B +=- c o s ()c o s

c o s

s i n s i

A B A B A B -=+ tan tan tan()1tan tan A B A B A B ++=

- tan tan tan()1tan tan A B

A B A B --=+

cot cot 1cot()cot cot A B A B B A ?-+=

+ cot cot 1

cot()cot cot A B A B B A ?+-=- 2.二倍角公式

sin 22sin cos A A A = 2222cos 2cos sin 12sin 2cos 1A A A A A =-=-=- 2

2tan tan 21tan A

A A

- 3.半角公式

sin

2A = cos 2A =

sin tan

21cos A A A ==+ sin cot 21cos A A A

==- 4.和差化积公式

sin sin 2sin

cos 22a b a b a b +-+=? sin sin 2cos sin

a b a b

a b +--=?

cos cos 2cos

cos 22a b a b a b +-+=? cos cos 2sin sin

a b a b

a b +--=-? ()

sin tan tan cos cos a b a b a b

++=?

5.积化和差公式

()()1sin sin cos cos 2a b a b a b =-+--???? ()()1

cos cos cos cos 2a b a b a b =++-????

()()1s i n c o s s i n s i n 2a b a b a b =++-???? ()()1

c o s s i n s i n s i n 2

a b a b a b =+--???? 6.万能公式

22tan

2sin 1tan 2

a a

+ 2

1tan 2cos 1tan 2a a a -=+ 22t a n

2t a n 1t a n 2

a a =- 7.平方关系

22sin cos 1x x += 22sec n 1x ta x -= 22csc cot 1x x -=

8.倒数关系

tan cot 1x x ?= sec cos 1x x ?= c sin 1cs x x ?=

9.商数关系

sin tan cos x x x =

cos cot sin x

x x

= 二、重要公式（1）0sin lim 1x x

x →= （2）()1

0lim 1x x x e →+= （3

）)1n a o >=

（4

）1n = （5）limarctan 2

x x π

→∞

（6）lim tan 2

x arc x π

→-∞

（7）limarccot 0x x →∞= （8）lim arccot x x π→-∞= （9）lim 0x

x e →-∞

（10）lim x

x e →+∞

=∞ （11）0

lim 1x

x x +

→=

三、下列常用等价无穷小关系（0x →）

sin x

x tan x x a r c s i n x

x arctan x x 2

11c o s

x x -

()

ln 1x x + 1x e x - 1

l n x a x a - ()11x x ?

+-?

四、导数的四则运算法则

()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-??= ???

五、基本导数公式

⑴()0c '= ⑵1

x x

μμ-= ⑶()sin cos x x '=

⑷()cos sin x x '=- ⑸()2

tan sec x x '= ⑹()2

cot csc x x '=- ⑺()sec sec tan x x x '=? ⑻()csc csc cot x x x '=-?

⑼()x

'= ⑽()ln x

a '= ⑾()1

ln x x

⑿(

log ln x

x a

'= ⒀(

)arcsin x '= ⒁(

)arccos x '=⒂()21arctan 1x x '=

+ ⒃()2

1arccot 1x x '=-+⒄()1x '=

⒅

八、微分公式与微分运算法则 ⑴()0d c = ⑵()1

d x

dx μ

μμ-= ⑶()sin cos d x xdx =

⑷()cos sin d x xdx =- ⑸()2

tan sec d x xdx = ⑹()2

cot csc d x xdx =- ⑺()sec sec tan d x x xdx =? ⑻()csc csc cot d x x xdx =-? ⑼()x

x d e

e dx = ⑽()ln x x d a a adx = ⑾()1

ln d x dx x

⑿(

log ln x

d dx x a =

⒀(

)arcsin d x =

⒁(

)arccos d x = ⒂()21arctan 1d x dx x =

+ ⒃()2

arccot 1d x dx x

=-+ 九、微分运算法则

⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2

u vdu udv

d v v -??=

???