一次函数动点问题-精心总结版

1、直线3

y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运

动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．

（1）直接写出A B 、两点的坐标；

（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式；

（3）当48

S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点

M 的坐标．

（2）设经过x 秒后点P 与点Q 第一次相遇，由题意，得

32104

x x =+?，解得803x =秒．∴点P 共运动了80

3803

?=厘米．

∵8022824=?+，∴

点P 、点Q 在AB 边上相遇，∴经过80

秒点P 与点

Q 第一次在边AB 上

相遇

2解（1）A （8，0）B （0，6）（2）86OA OB ==Q ，10AB ∴=

Q 点Q 由O 到A 的时间是

881=（秒）∴点P 的速度是610

+=（单位/秒）当P 在线段OB 上运动（或03t ≤≤）时，2OQ t OP t ==， 2S t =

当P 在线段BA 上运动（或38t <≤）时，6102162OQ t AP t t ==+-=-，, 如图，作PD OA ⊥于点D ，由

PD AP BO AB =

，得4865

PD -=， 21324

255S OQ PD t t ∴=?=-+

（3）82455P ?? ???，12382412241224555555I M M 2??????

-- ? ? ???

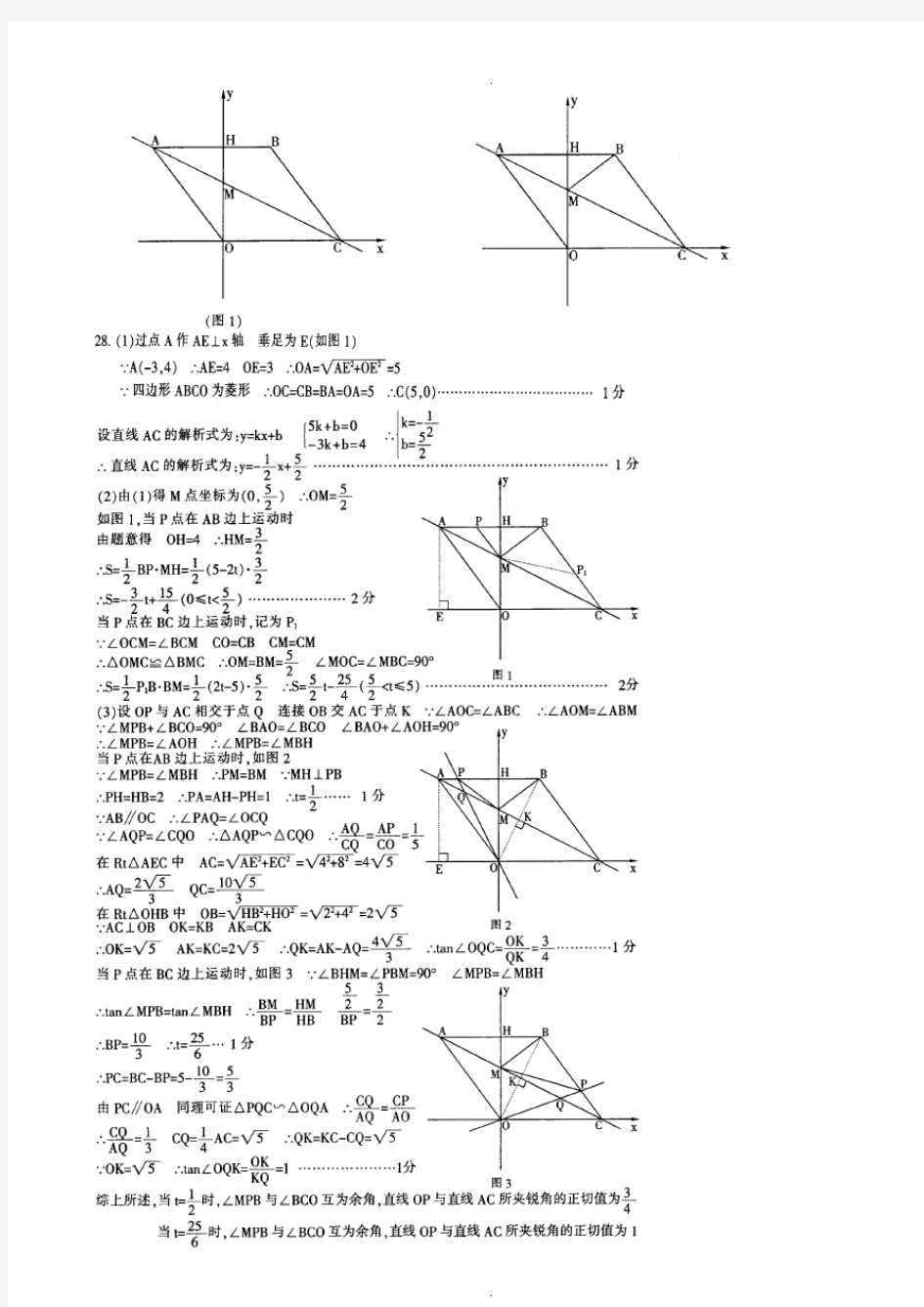
????，，，，， 2 如图1，在平面直角坐标系中，点O 是坐标原点，四边形ABCO 是菱形，点A 的坐标为（－3，4），

点C 在x 轴的正半轴上，直线AC 交y 轴于点M ，AB 边交y 轴于点H ．（1）求直线AC 的解析式；

（2）连接BM ，如图2，动点P 从点A 出发，沿折线ABC 方向以2个单位／秒的速度向终点C 匀速运动，设△PMB 的面积为S （S ≠0），点P 的运动时间为t 秒，求S 与t 之间的函数关系式（要求写出自变量t 的取值范围）；

（3）在（2）的条件下，当 t 为何值时，∠MPB 与∠BCO 互为余角，并求此时直线OP 与直线AC 所夹锐角的正切值．

3.（2010年金华）如图，把含有30°角的三角板ABO 置入平面直角坐标系中，A ，B 两点坐标分别为（3，0）和(0，

.动点P 从A 点开始沿折线AO-OB-BA 运动，点P 在AO ，OB ，BA 上运动的速度分别为1

2 (长度单位/秒)﹒一直尺的上边缘l 从x 轴的位置开始以

(长度单位/秒)的速度向上平行移动（即移动过程中保持l ∥x 轴），且分别与OB ，AB 交于E ，F 两

点﹒设动点P 与动直线l 同时出发，运动时间为t 秒，当点P 沿折线AO -OB -BA 运动一周时，直线l 和动点P 同时停止运动．请解答下列问题：

（1）过A ，B 两点的直线解析式是 ▲ ；

（2）当t ﹦4时，点P 的坐标为 ▲ ；当t ﹦ ▲ ，点P 与点E 重合；（3）① 作点P 关于直线EF 的对称点P′. 在运动过程中，若形成的四边形PEP′F 为

菱形，则t 的值是多少？

② 当t ﹦2时，是否存在着点Q

解：（1）333+-=x

y ；

（2）（0,3），2

（3）①当点P 在线段AO 上时，过F 作FG ⊥G 为垂足（如图1）

∵FG OE =,FP EP =,∠=EOP ∠FGP ∴△EOP ≌△FGP ，∴PG OP =﹒

又∵t FG OE 33

=,∠=A 60°,∴AG 而t AP =，∴t OP -=3,t AG AP PG 3

=-= 由t t 3

3=-得 59=t ；

当点P 在线段OB 当点P 在线段BA 上时，

过P 作PH ⊥EF ，PM ⊥OB ，H 、 ∵t OE 33=

,∴t BE 33

33-=,∴tan t BE EF =

∴6

921t EF EH MP -===，又∵(2-=t BP 在Rt△BMP 中，MP BP =?0

60cos

即6

921)6(2t

t -=?-，解得745=t

②存在﹒理由如下：

∵2=t ，∴33

OE ,2=AP ，1=OP 将△BEP 绕点E 顺时针方向旋转90°，得到 △EC B '（如图3）

∵OB ⊥EF ，∴点B '在直线EF 上，

C 点坐标为（

332，33

2－1）过F 作FQ ∥C B '，交EC 于点Q , 则△FEQ ∽△EC B '

图1

由

='=QE CE FE E B FE BE ，可得Q 的坐标为（－3

，33）根据对称性可得，Q 关于直线EF 的对称点Q '（－3

，3）也符合条件

9．（2010，浙江义乌）如图1，已知∠ABC ＝90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B 不重合），连结

AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F .

（1）如图2，当BP ＝BA 时，∠EBF ＝ ▲ °，猜想∠QFC ＝ ▲ °；

（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB ＝32，设BP ＝x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．

第9题【答案】（1）=∠EBF 30°.QFC ∠＝ 60° （2）QFC ∠＝60°

不妨设BP ＞3AB , 如图1所示 ∵∠BAP ＝∠BAE+∠EAP ＝60°+∠EAP ∠EAQ ＝∠QAP+∠EAP ＝60°+∠EAP

∴∠BAP ＝∠EAQ

在△ABP 和△AEQ 中 AB ＝AE ，∠BAP ＝∠EAQ ， AP ＝AQ ∴△ABP ≌△AEQ （SAS ） ∴∠AEQ ＝∠ABP ＝90°

∴∠BEF 180180906030AEQ AEB =?-∠-∠=?-?-?=? ∴QFC ∠＝∠EBF +∠BEF ＝30°+30°＝60°

(事实上当BP ≤3AB 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分）(3) 在图1中，过点F 作FG ⊥

BE 于点G

∵△ABE 是等边三角形 ∴BE ＝AB ＝32

，由（1）得=∠EBF 30°

在Rt △BGF 中，32

BE BG

= ∴BF ＝

2cos30BG

=? ∴EF ＝2 ∵△ABP ≌△AEQ ∴QE ＝BP ＝x ∴QF ＝QE ＋EF 2x =+

过点Q 作QH ⊥BC ，垂足为H

在Rt △QHF 中，3

sin 60(2)2

y QH QF x ==?=+g （x ＞0）即y 关于x 的函数关系式是：3

y x =+

11已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；

解（Ⅰ）如图①，折叠后点B 与点A 重合，则ACD BCD △≌△.

设点C 的坐标为()()00m m >，.则4BC OB OC m =-=-. 于是4AC BC m ==-.

在Rt AOC △中，由勾股定理，得2

AC OC OA =+，

即()2

42m m -=+，解得32m =

.∴点C 的坐标为302??

???

，（Ⅱ）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；

（Ⅱ）如图②，折叠后点B 落在OA 边上的点为B ',

则B CD BCD '△≌△.由题设OB x OC y '==，，则

B C BC y '

==-，

在Rt B OC '△中，由勾股定理，得222B C OC OB ''=+.()24y ∴-

即2

128

y x =-

+ 由点B '在边OA 上，有02x ≤≤， ∴ 解析式21

28y x =-+()02x ≤≤为所求.Q 当02x ≤≤时，y 随x 的增大而减小，

y ∴的取值范围为3

y ≤≤.

（Ⅲ）若折叠后点B 落在边OA 上的点为B '，且使B D OB '∥，求此时点C 的坐标．

（Ⅲ）如图③，折叠后点B 落在OA 边上的点为B ''，且B D OB ''∥. 则OCB CB D ''''∠=∠.

又CBD CB D OCB CBD ''''∠=∠∴∠=∠Q ，，有CB BA ''∥.

Rt Rt COB BOA ''∴△∽△.有

OB OC

OA OB

''=，得2OC OB ''=. 在Rt B OC ''△中，

设()00OB x x ''=>，则02OC x =.由（Ⅱ）的结论，得2

001228

x x =-+，解得000808x x x =-±>∴=-+，

∴点C 的坐标为()

016.

复变函数总结

第一章复数的运算与复平面上的拓扑 1.复数的定义一对有序实数（x,y ）构成复数z x iy =+,其中()()Re ,Im x z y z ==.21i =-， X 称为复数的实部，y 称为复数的虚部。复数的表示方法 1）模： z = 2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值 ()arg z 是位于(,]ππ-中的幅角。 3）()arg z 与 arctan y x 之间的关系如下：当0,x > arg arctan y z x =；当0,arg arctan 0,0,arg arctan y y z x x y y z x ππ? ≥=+??

4）若 12 1122,i i z z e z z e θθ==, 则 () 121212i z z z z e θθ+=； ()121122 i z z e z z θθ-= 5.无穷远点得扩充与扩充复平面复平面对内任一点z , 用直线将z 与N 相连, 与球面相交于P 点, 则球面上除N 点外的所有点和复平面上的所有点有一一对应的关系, 而N 点本身可代表无穷远点, 记作∞.这样的球面称作复球面这样的球面称作复球面. 扩充复平面---引进一个“理想点”: 无穷远点 ∞ 复平面的开集与闭集复平面中领域，内点，外点，边界点，聚点，闭集等概念复数序列的极限和复数域的完备性复数的极限，，柯西收敛定理，魏尔斯特拉斯定理，聚点定理等从实数域里的推广，可以结合实数域中的形式来理解。第二章复变量函数 1.复变量函数的定义 1）复变函数的反演变换（了解） 2）复变函数性质反函数有界性周期性， 3）极限与连续性极限：连续性 2.复变量函数的形式偏导 1）复初等函数 ). ( ),( , , , , . z f w z w iv u w z G iy x z G =+=+=记作复变函数简称的函数是复变数那末称复变数之对应与就有一个或几个复数每一个复数中的对于集合按这个法则个确定的法则存在如果有一的集合是一个复数设. )( )(,)0(0 )( ,0 , , 0 )( 0000时的极限趋向于当为那末称有时使得当相应地必有一正数对于任意给定的存在如果有一确定的数内的去心邻域定义在设函数z z z f A A z f z z A z z z z f w ερδδεδερ<-≤<<-<><-<= . )( , )( . )( ),()(lim 000 内连续在我们说内处处连续在区域如果处连续在那末我们就说如果D z f D z f z z f z f z f z z =→

(完整版)复变函数知识点梳理解读

第一章:复数与复变函数这一章主要是解释复数和复变函数的相关概念,大部分内容与实变函数近似,不难理解。一、复数及其表示法介绍复数和几种新的表示方法,其实就是把表示形式变来变去,方便和其他的数学知识联系起来。二、复数的运算高中知识,加减乘除,乘方开方等。主要是用新的表示方法来解释了运算的几何意义。三、复数形式的代数方程和平面几何图形就是把实数替换成复数,因为复数的性质,所以平面图形的方程式二元的。四、复数域的几何模型——复球面将复平面上的点,一一映射到球面上,意义是扩充了复数域和复平面,就是多了一个无穷远点,现在还不知道有什么意义,猜想应该是方便将微积分的思想用到复变函数上。五、复变函数不同于实变函数是一个或一组坐标对应一个坐标,复变函数是一组或多组坐标对应一组坐标,所以看起来好像是映射在另一个坐标系里。六、复变函数的极限和连续性与实变函数的极限、连续性相同。第二章:解析函数

这一章主要介绍解析函数这个概念,将实变函数中导数、初等函数等概念移植到复变函数体系中。一、解析函数的概念介绍复变函数的导数,类似于实变二元函数的导数,求导法则与实变函数相同。所谓的解析函数,就是函数处处可导换了个说法,而且只适用于复变函数。而复变函数可以解析的条件就是:μ对x与ν对y的偏微分相等且μ对y和ν对x的偏微分互为相反数,这就是柯西黎曼方程。二、解析函数和调和函数的关系出现了新的概念:调和函数。就是对同一个未知数的二阶偏导数互为相反数的实变函数。而解析函数的实部函数和虚部函数都是调和函数。而满足柯西黎曼方程的两个调和函数可以组成一个解析函数,而这两个调和函数互为共轭调和函数。三、初等函数和实变函数中的初等函数形式一样,但是变量成为复数,所以有一些不同的性质。第三章:复变函数的积分这一章,主要是将实变函数的积分问题,在复变函数这个体系里进行了系统的转化,让复变函数有独立的积分体系。但是很多知识都和实变函数的知识是类似的。可以理解为实变函数积分问题的一个兄弟。一、复积分的概念复积分就是复变函数的积分,实质是两个实二型线积分。所以应该具有相应的实二型线积分的性质。复积分存在的充分条件是实部函数和虚部函数都连续。二、柯西积分定理

寄生虫-寄生虫总结完整版(网上来的)

寄生虫总结阅读笔记：红色部分：历年考题涉及的内容红色部分：历年考题中比较重要的内容蓝色部分：是课上老师强调的比较重要的内容蓝色部分：是老师强调的重要的概念or是历年考试的大题例题黑色部分：了解就可以的内容（为了保持学习内容的完整性）黑色部分：原理，概念，专用名词和标题等等绿色部分：备注灰色部分：貌似大课没有讲，实习课时候讲过考试的时候有的题型会是英文的，本总结里面用的都是中文，所以最好尽可能的掌握总结中出现过的英文名词。根据历年考试经验，题目大多出自于应试指南，所以该练习册很有参考价值。总体上寄生虫内容还是比较少的，用两三天的时间复习应该就没有问题了。加油，祝考出理想的成绩~ 第一节总论 1.Notes on the Powerpoint 1. 医学寄生虫学分为：医学原虫学、医学蠕虫学、医学节肢动物学 2. TDR、世界卫生组织重点防治的五种寄生虫病：疟疾（malaria）血吸虫病（schistosomiasis) 丝虫病（filariasis) 锥虫病（trypanosomiasis) 利什曼病（leishmaniasis） 3.我国建国初期五大寄生虫病：疟疾（malaria）血吸虫病（schistosomiasis) 丝虫病（filariasis) 钩虫病（hookworm disease) 利什曼病（leishmaniasis） 4. 概念：寄生现象（parasitism）：两种生物间共同生活的三种方式互利共生（mutualism）：双方均获益片利共生（commensalism）：一方获利，另一方既无益也无害寄生（parasitism）：一方获利，称寄生虫（parasite）；一方受害，称宿主（host）宿主的分类：终宿主（definitive host）：寄生虫成虫或有性生殖阶段寄生的宿主中间宿主（intermediate host）：寄生虫幼虫或无性生殖阶段寄生的宿主保虫宿主（reservoir host）：强调是脊椎动物转续宿主（paratenic host）：非正常宿主，蠕虫感染宿主能存活但不能发育

高考复习函数知识点总结

高考复习函数知识点总结一．函数概念的理解以及函数的三要素（1）函数的概念 ①设A 、B 是两个非空的数集，如果按照某种对应法则f ，对于集合A 中任何一个数x ，在集合B 中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →． ②函数的三要素:定义域、值域和对应法则． ③只有定义域相同，且对应法则（函数关系式）也相同的两个函数才是同一函数．（2）区间的概念及表示法 ①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a x b <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做 [,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做 [,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b < ．（3）求函数的定义域时，一般遵循以下原则： ① 分式的分母不为0； ② 偶次根式下被开方数大于0； ③ 0y x = ，则有0x ≠ ； ④ 对数函数的真数大于0，底数大于0切不等于1 注意：①解析式为整式的函数定义域为R ； ②若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则

其定义域一般是各基本初等函数的定义域的交集； ③对于求复合函数定义域问题，一般步骤是：若已知() f x的定义域为[,] a g x b ≤≤解出． f g x的定义域应由不等式() a b，其复合函数[()] （4）求函数的值域或最值常用方法： ①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值． ②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值． ③判别式法：若函数() =可以化成一个系数含有y的关于x的二次方程 y f x 2 ++=，则在()0 a y x b y x c y ()()()0 a y≠时，由于,x y为实数，故必须有 2()4()()0 ?=-?≥，从而确定函数的值域或最值． b y a y c y ④不等式法：利用基本不等式确定函数的值域或最值． ⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题． ⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．（5）函数解析式 ①换元法；（用于求复合函数的解析式） ②配凑法；（用于求复合函数的解析式）

复变函数学习指导书

复变函数复习提纲 (一)复数的概念 1.复数的概念：z x iy =+，,x y 是实数, ()()Re ,Im x z y z ==.2 1i =-. 注：两个复数不能比较大小. 2.复数的表示 1 ）模：z = 2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ-中的幅角。 3）()arg z 与arctan y x 之间的关系如下：当0,x > arg arctan y z x =；当0,arg arctan 0,0,arg arctan y y z x x y y z x ππ? ≥=+??

(完整版)【工程数学】复变函数复习重点

复变函数复习重点 (一)复数的概念 1.复数的概念：z x iy =+，,x y 是实数, ()()Re ,Im x z y z ==.21i =-. 注：一般两个复数不比较大小，但其模（为实数）有大小. 2.复数的表示 1）模：z = 2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ-中的幅角。 3）()arg z 与arctan y x 之间的关系如下：当0,x > arg arctan y z x =；当0,arg arctan 0,0,arg arctan y y z x x y y z x ππ? ≥=+??

高中数学函数知识点总结

高中数学函数知识点总结（1）高中函数公式的变量：因变量，自变量。在用图象表示变量之间的关系时，通常用水平方向的数轴上的点自变量，用竖直方向的数轴上的点表示因变量。（2）一次函数：①若两个变量 ,间的关系式可以表示成（为常数，不等于0）的形式，则称是的一次函数。②当 =0时，称是的正比例函数。（3）高中函数的一次函数的图象及性质 ①把一个函数的自变量与对应的因变量的值分别作为点的横坐标与纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象。 ②正比例函数 =的图象是经过原点的一条直线。 ③在一次函数中，当 0， O，则经2、3、4象限；当 0， 0时，则经1、 2、4象限；当 0， 0时，则经1、 3、4象限；当 0， 0时，则经1、2、3象限。 ④当 0时，的值随值的增大而增大，当 0时，的值随值的增大而减少。（4）高中函数的二次函数： ①一般式： ( )，对称轴是顶点是； ②顶点式： ( )，对称轴是顶点是； ③交点式： ( )，其中（），（）是抛物线与x轴的交点（5）高中函数的二次函数的性质 ①函数的图象关于直线对称。 ②时，在对称轴（）左侧，值随值的增大而减少；在对称轴（）右侧；的值随值的增大而增大。当时，取得最小值

③时，在对称轴（）左侧，值随值的增大而增大；在对称轴（）右侧；的值随值的增大而减少。当时，取得最大值 9 高中函数的图形的对称（1）轴对称图形：①如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴。②轴对称图形上关于对称轴对称的两点确定的线段被对称轴垂直平分。（2）中心对称图形：①在平面内，一个图形绕某个点旋转180度，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做他的对称中心。②中心对称图形上的每一对对应点所连成的线段都被对称中心平分。

《复变函数》总结

复变小结 1.幅角（不赞成死记，学会分析） .2 argtg 20,0,0,0,arctg 0,0,20,arctg arg ππ πππ<<-???? ?????=<≠<±≠=±>=x y y x y x x y y x x x y z 其中 -∏

b.对于P12例题 1.11可理解为高中所学的平面上三点（A,B,C ）共线所满足的公式: (向量) OC=tOA+（1-t ）OB=OB+tBA c.对于P15例题1.14中可直接转换成X 和Y 的表达式后判断正负号来确定其图像。 d.判断函数f(z)在区域D 内是否连续可借助课本P17定义1.8 4.解析函数，指数，对数，幂、三角双曲函数的定义及表达式，能熟练计算，能熟练解初等函数方程 a.在某个区域内可导与解析是等价的。但在某一点解析一定可导，可导不一定解析。 b.柯西——黎曼条件，自己牢记:（注意那个加负那个不加） c.指数函数:复数转换成三角的定义。 d.只需记住：Lnz=ln[z]+i(argz+2k π) e.幂函数：底数为e 时直接运算（一般转换成三角形式）当底数不为e 时，w= z a = e aLnz (幂指数为Ln 而非ln) 能够区分：的计算。 f.三角函数和双曲函数：只需记住：及其他可自己试着去推导一下。反三角中前三个最好自己记住，特别 iz iz i z -+-=11Ln 2Arctg 因为下一章求积分会用到 11)(arctan ,2+=z z (如第三章的习题9) 5.复变函数的积分 ,,,i e e i i e i ππ+)15.2(.2e e sin ,2e e cos i z z iz iz iz iz ---=+=???????=-==+=--y i i iy y iy y y y y sh 2e e sin ch 2e e cos

复变函数总结完整版

第一章复数 1 i 2=-1 i = ?, -1 欧拉公式z=x+iy 实部Re Z 虚部Im Z 2运算① z1≡z2^ Rez1=Rez2Imz1=Imz2 ②(z1±z2)=Re(z1±z2)+lm(z1±z2)= (Rez1±Rez2)+(lm z1+ Im Z2) 乙Z2 ③=χ1 iy1 χ2 iy2 X1X2iχ1y2iχ2y1- y1y2 =X1X2 -y』2 i χ1y2 χ2y1 ④z1 _ z1z2 一χ1 i y1 χ2 -iy2 _ χ1χ2 y1y2 i y1χ2 -χ1y2 2 2 2 2 Z2 Z2Z2 χ2 iy2 χ2 -iy2 χ2 y2 χ2 y2 ⑤z = X - iy 共轭复数 z z =(x+iy I x — iy )=χ2+ y2共轭技巧运算律P1页 3代数，几何表示 ^X iy Z与平面点χ,y-------- 对应，与向量--- 对应辐角当z≠0时，向量Z和X轴正向之间的夹角θ ,记作θ =Arg z= V0■ 2k二k= ± 1 ± 2± 3… 把位于-∏v二0≤∏的厲叫做Arg Z辐角主值记作^0= argz0 4如何寻找arg Z π 例：z=1-i 4 π z=i 2 π z=1+i 4 z=-1 π 5 极坐标: X = r CoSr , y = r sin 二Z=Xiy = r COSr isin

利用欧拉公式e i 71 =COS71 i Sin71 例2 f Z = C 时有(C )=0

可得到z= re° Z z2=r1e i J r2e i72=r1r2e iτe i72= r1r2e i 71'y^ 6高次幂及n次方 n n in 「n Z Z Z Z ............ z=re r COS 1 Sin nv 凡是满足方程国=Z的ω值称为Z的n次方根，记作CO =^Z ☆当丄二f Z o时，连续例1 证明f Z =Z在每一点都连续证：f（Z f（Z o ）= Z - Z o = Z - Z o τ 0ZT Z o 所以f z = Z在每一点都连续 3导数 f Z o Jm fZ 一 f z o z-?z°Z-Z o ,2 n 第二章解析函数 1极限 2函数极限 ①复变函数对于任一Z- D都有W FP与其对应川=f Z 注：与实际情况相比，定义域，值域变化例f z = z Z—Z o 称f Z当Z-:Z o时以A为极限 df(z l Z=Zo 1

人体寄生虫学总结归纳_共4页

(一)在我国能引起肝脏损伤的寄生虫有哪些?各是由哪个阶段造成的? 刚地弓形虫滋养体(速殖子)、、溶组织内阿米巴滋养体、华枝睾吸虫成虫、日本血吸虫卵、杜氏利什曼原虫无鞭毛体?斯氏狸殖吸虫童虫、细粒棘球绦虫棘球蚴、似蚓蛔线虫成虫异位寄生于肝胆管。 (二)在我国能引起肺脏损害的寄生虫有哪些?各是由哪个阶段造成的? 刚地弓形虫滋养体(速殖子)、溶组织内阿米巴滋养体、卫氏并殖吸虫成虫、日本血吸虫虫卵、细粒棘球绦虫棘球蚴、卡氏肺孢子虫滋养体和包囊、旋毛形线虫、钩虫和似蚓蛔线虫幼虫游移至肺。 (三)在我国能引起眼损伤的寄生虫有哪些?各是由哪个阶段造成的? 刚地弓形虫滋养体(速殖子)、细粒棘球绦虫棘球蚴、链状带绦虫囊尾蚴、曼氏迭宫绦虫裂头蚴、蝇蛆、结膜吸吮线虫成虫。 (四)在我国以贫血为主要临床表现的寄生虫有哪些?其贫血机制有何不同? 在我国以贫血为主要临床表现的寄生虫有钩虫、疟原虫和杜氏利什曼原虫。钩虫贫血机理①钩虫口囊内有钩齿或板齿咬附、破坏肠粘膜并吸血。②钩虫吸血时，分泌抗凝素，加重血液的丢失。③因钩虫寄生造成人丢失的血量，为吸血量、移位伤口渗血量、咬附点渗血量和偶尔肠粘膜大面积渗血量的总和。每条十二指肠钩口线虫每日所致失血量为0.14～0.4d，而美洲板口线虫为0.01～0.1m1。④钩虫破坏肠粘膜，影响营养成分的吸收，加重贫血的发生。⑤宿主全身营养不佳时，虽有少量钩虫寄生，也可出现贫血。疟原虫贫血机理①疟原虫直接破坏，每完成一个红细胞内裂体增殖周期，就破坏大量红细胞，以恶性疟原虫破坏红细胞为重。②脾肿大，脾功能亢进，破坏血细胞的能力增强。③免疫溶血。④骨髓造血功能受抑制。杜氏利什曼原虫贫血机理①脾肿大，脾功能亢进，破坏血细胞能力增强。②免疫溶血。③骨髓造血功能受抑制。 (五)在我国能引起脑部损害的寄生虫有哪些?各是由哪个阶段造成的? 刚地弓形虫滋养体(速殖子)、溶组织内阿米巴滋养体、疟原虫(脑型疟主要由恶性疟原虫引起，而间日疟偶发)红细胞内期、卫氏并殖吸虫童虫和成虫、日本血吸虫虫卵、细粒棘球绦虫棘球蚴、链状带绦虫囊尾蚴、旋毛形线虫幼虫。 (六)粪便检查时，主要能发现哪些寄生虫卵? 似蚓蛔线虫卵、钩虫卵、毛首鞭形线虫卵、日本血吸虫卵、卫氏并殖吸虫卵、华枝睾吸虫卵、布氏姜片虫卵和微小膜壳绦虫卵。 (七)人粪处理不当能引起哪些寄生虫病的流行? 蛔虫病、钩虫病、鞭虫病、肺吸虫病、血吸虫病、肝吸虫病、肠吸虫病、猪带绦虫病和囊虫病、牛带绦虫病、微小膜壳绦虫病、阿米巴痢疾、贾第虫病、隐孢子虫病、结肠小袋纤毛虫病。 (八)在人肠道内寄生的寄生虫主要有哪些? 似蚓蛔线虫、钩虫、毛首鞭形线虫、蠕形住肠线虫、旋毛形线虫、布氏姜片吸虫、链状带绦虫、肥胖带绦虫、微小膜壳绦虫、曼氏迭宫绦虫、溶组织内阿米巴、蓝氏贾第鞭毛虫、隐孢子虫和结肠小袋纤毛虫。

初高中函数知识点总结大全

初高中函数知识点总结大全正比例函数形如y=kx （k为常数，k≠0）形式，y是x的正比例函数。 1.定义域:R(实数集) 2.值域:R(实数集) 3.奇偶性:奇函数 4.单调性: 当k>0时，图像位于第一、三象限，y随x的增大而增大(单调递增);当k<0时，图像位于第二、四象限，y随x的增大而减小(单调递减)。一次函数一、定义及定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。特别地，当b=0时，y是x的正比例函数。即：y=kx （k为常数，k ≠0）一次函数及正比例函数的识别方法：若y=kx+b(k,b是常数，k≠0)，那么y叫做x的一次函数，特别的，当b=0时，一次函数就成为y=kx(k是常数，k≠0)，这时，y叫做x的正比例函数，当k=0时，一次函数就成为若y=b，这时，y叫做常函数。 ☆A及B成正比例A=kB(k≠0) 二、一次函数的性质：

1.y的变化值及对应的x的变化值成正比例，比值为k，即：y=kx+b （k 为任意不为零的实数 b取任何实数） 2.当x=0时，b为函数在y轴上的截距。三、一次函数的图像及性质： 1．作法及图形：通过如下3个步骤（1）列表；（2）描点；（3）连线，可以做出一次函数的图像——一条直线。因此，作一次函数的图像只需知道2点，并连成直线即可。（通常找函数图像及x 轴和y轴的交点） 2．性质：（1）在一次函数上的任意一点P（x，y），都满足等式：y=kx+b。（2）一次函数及y轴交点的坐标总是（0，b)，及x轴总是交于（-b/k，0）正比例函数的图像总是过原点。 3．k，b及函数图像所在象限：当k＞0时，直线必通过一、三象限，y随x的增大而增大；当k＜0时，直线必通过二、四象限，y随x的增大而减小。当b＞0时，直线必通过一、二象限；当b=0时，直线通过原点当b＜0时，直线必通过三、四象限。特别地，当b=0时，直线通过原点O（0，0）表示的是正比例函数的图像。

(完整版)复变函数第六章留数理论及其应用知识点总结

第六章留数理论及其应用 §1.留数 1.（定理6.1 柯西留数定理）： ∫f(z)dz=2πi∑Res(f(z),a k) n k=1 C 2.（定理6.2）：设a为f(z)的m阶极点， f(z)= φ(z) (z?a)n , 其中φ(z)在点a解析，φ(a)≠0，则 Res(f(z),a)=φ(n?1)(a) (n?1)! 3.（推论6.3）：设a为f(z)的一阶极点， φ(z)=(z?a)f(z),则 Res(f(z),a)=φ(a) 4.（推论6.4）：设a为f(z)的二阶极点 φ(z)=(z?a)2f(z)则 Res(f(z),a)=φ′(a) 5.本质奇点处的留数：可以利用洛朗展式 6.无穷远点的留数： Res(f(z),∞)= 1 2πi ∫f(z)dz Γ? =?c?1 即，Res(f(z),∞)等于f(z)在点∞的洛朗展式中1 z 这一项系数的反号 7.（定理6.6）如果函数f(z)在扩充z平面上只有有限个孤立奇点（包括无穷远点在内），设为a1,a2,…,a n,∞,则f(z)在各点的留数总和为零。注：虽然f(z)在有限可去奇点a处，必有Res(f(z),∞)=0，但是，如果点∞为f(z)的可去奇点（或解析点），则Res(f(z),∞)可以不为零。 8.计算留数的另一公式：

Res (f (z ),∞)=?Res (f (1t )1t 2,0) §2.用留数定理计算实积分一.∫R (cosθ,sinθ)dθ2π0型积分 → 引入z =e iθ 注：注意偶函数二.∫P(x)Q(x)dx +∞?∞型积分 1.（引理6.1 大弧引理）：S R 上 lim R→+∞zf (z )=λ 则 lim R→+∞∫f(z)dz S R =i(θ2?θ1)λ 2.（定理6.7）设f (z )=P (z )Q (z )为有理分式，其中 P (z )=c 0z m +c 1z m?1+?+c m (c 0≠0) Q (z )=b 0z n +b 1z n?1+?+b n (b 0≠0) 为互质多项式，且符合条件：（1）n-m ≥2; （2）Q(z)没有实零点于是有 ∫ f (x )dx =2πi ∑Res(f (z ),a k )Ima k >0 +∞ ?∞ 注：lim R→R+∞ ∫f(x)dx +R ?R 可记为P.V.∫f(x)dx +∞?∞ 三. ∫P(x)Q(x)e imx dx +∞?∞ 型积分 3.（引理6.2 若尔当引理）：设函数g(z)沿半圆周ΓR :z =Re iθ(0≤θ≤π，R 充分大)上连续，且 lim R→+∞g (z )=0 在ΓR 上一致成立。则 lim R→+∞ ∫g(z)e imz dz ΓR =0 4.（定理6.8）：设g (z )=P (z )Q (z )，其中P(z)及Q(z)为互质多项式，且符合条件：

复变函数积分方法总结

复变函数积分方法总结The final revision was on November 23, 2020

复变函数积分方法总结经营教育乐享 [选取日期] 复变函数积分方法总结数学本就灵活多变，各类函数的排列组合会衍生多式多样的函数新形势，同时也具有本来原函数的性质，也会有多类型的可积函数类型，也就会有相应的积分函数求解方法。就复变函数： z=x+iy i2=-1 ，x,y分别称为z的实部和虚部，记作x=Re(z),y=Im(z)。arg z=θθ称为主值 -π＜θ≤π，Arg=argz+2kπ。利用直角坐标和极坐标的关系式x=rcosθ，y=rsinθ,故z= rcosθ+i rsinθ；利用欧拉公式 e iθ=cosθ+isinθ。z=re iθ。 1.定义法求积分：定义：设函数w=f(z)定义在区域D内，C为区域D内起点为A终点为B 的一条光滑的有向曲线，把曲线C任意分成n个弧段，设分点为A=z0，

z 1，…，z k-1，z k ，…，z n =B ，在每个弧段z k-1 z k (k=1,2…n)上任取一点k 并作和式S n =∑f( k )n k?1(z k -z k-1)= ∑f( k )n k?1z k 记 z k = z k - z k-1，弧段z k-1 z k 的长度 δ=max 1≤k≤n {S k }(k=1,2…,n),当 δ→0时，不论对c 的分发即k 的取法如何，S n 有唯一的极限，则称该极限值为函数f(z)沿曲线C 的积分为： ∫f(z)dz c =lim δ 0 ∑f(k )n k?1z k 设C 负方向(即B 到A 的积分记作) ∫f(z)dz c?.当C 为闭曲线时，f(z)的积分记作∮f(z)dz c (C 圆周正方向为逆时针方向) 例题：计算积分1)∫dz c 2) ∫2zdz c ,其中C 表示a 到b 的任一曲线。（1）解：当C 为闭合曲线时，∫dz c =0. ∵f(z)=1 S n =∑f(k)n k?1(z k -z k-1)=b-a ∴lim n 0 Sn =b-a,即1)∫dz c =b-a. (2)当C 为闭曲线时，∫dz c =0. f(z)=2z;沿C 连续，则积分∫zdz c 存在，设k =z k-1,则 ∑1= ∑Z n k?1（k ?1）(z k -z k-1) 有可设k =z k ，则 ∑2= ∑Z n k?1（k ?1）(z k -z k-1) 因为S n 的极限存在，且应与∑1及∑2极限相等。所以 S n = (∑1+∑2)= ∑k?1n z k (z k 2?z k?12)=b 2-a 2 ∴ ∫2zdz c =b 2-a 2 定义衍生1：参数法： f(z)=u(x,y)+iv(x,y), z=x+iy 带入∫f(z)dz c 得：

寄生虫实验总结

寄生虫实验总结医学原虫（油镜观察）溶组织内阿米巴【观察结构：包囊】形态特点：未成熟糖原泡、拟染色体成熟包囊为四核感染阶段：成熟四核包囊感染特点：经口、口腔性行为寄生部位：盲肠、升结肠、乙状结肠终宿主：人实验诊断：生理盐水：滋养体碘液涂片：包囊镜下特点：球形，包囊内有泡状核蓝氏贾第鞭毛虫（贾第虫）【观察结构：包囊】形态特征：蓝色染液，呈椭圆形，囊壁较厚，与虫体间有明显间隙感染阶段：4 核成熟包囊致病阶段：滋养体感染途径：经口寄生部位：十二指肠及小肠上段终宿主：人或某些哺乳动物实验诊断：粪便检查（生理盐水涂片检查滋养体，碘液涂片检查包囊）、小肠液检查、小肠活体组织检查阴道毛滴虫【观察结构：滋养体】形态特点:呈梨形,5根鞭毛,泡状核上缘有5个毛基体,发出5根鞭毛,后鞭毛与波动膜相连感染阶段:滋养体致病阶段：滋养体感染途径: 直接接触:性传播间接接触:公共泳衣泳裤、坐式马桶、公共浴盆等寄生部位：女性：阴道后穹男性：尿道、前列腺、睾丸、附睾实验诊断：生理盐水直接涂片、姬氏染色涂片、培养基培养镜下检查：蓝色（姬氏），梨形，轴柱伸出体外很明显，4根明显的鞭毛

疟原虫（红细胞内期形态）形态特点：早期滋养体：核小，胞质少，虫体环状晚期：细胞变大变淡，出现红色薛氏点未成熟滋养体：核开始分裂，空泡消失，疟色素开始集中成熟滋养体：红细胞胀大，有裂殖子，疟色素集中雌配子：圆形或卵圆形，胞质蓝色，核小致密，深红色，偏一侧，疟色素分散雄配子：圆形，胞质蓝略带红色，核大，疏松，疟色素分散感染阶段：子孢子感染特点：按蚊叮咬寄生部位：肝细胞，红细胞实验诊断：厚薄血涂片镜检（厚血涂片查虫，薄血片鉴别虫种）镜下特点：同形态特点医学蠕虫吸虫华支睾吸虫（10*40 ）【观察结构：虫卵】形态特点：形似芝麻，淡黄褐色，一端较宽且有盖，卵盖周围的卵壳增厚形成肩峰，另一端有小疣。卵小，卵内有毛蚴。感染阶段：囊蚴感染途径：经口中间宿主：第一中间宿主淡水螺（豆螺）第二中间宿主（淡水鱼，虾）终宿主：人和肉食类哺乳动物寄生部位：肝胆管内实验诊断：粪便直接涂片法镜下特点：在高倍镜下，有卵盖。淡黄褐色。姜片吸虫（10*10 ）【观察结构：虫卵】形态特点：虫卵椭圆形，吸虫中最大，淡黄色，卵盖薄而均匀，一端有一不明显小盖，卵内含有一个卵细胞和约20-40 个卵黄细胞。中间宿主：扁卷螺终宿主：人和猪感染阶段：囊蚴感染途径：经口寄生部位：人小肠实验诊断：粪便直接涂片法（检查虫卵）镜下特点：肥厚，淡黄色，吸虫中最大

高一数学必修一第二章基本初等函数知识点总结

第二章基本初等函数知识点整理〖2.1〗指数函数 2.1.1指数与指数幂的运算（1）根式的概念 ①如果,,,1n x a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n 表示；当n 是偶数时，正数a 的正的n n 次方根用符号0的n 次方根是0；负数 a 没有n 次方根． n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥． ③根式的性质：n a =；当n a =；当n 为偶数时， (0) || (0) a a a a a ≥?==? -∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m n n a a m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质 ①(0,,)r s r s a a a a r s R +?=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r a b a b a b r R =>>∈ 2.1.2指数函数及其性质（4）指数函数

〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义 ①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数． ②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =?=>≠>．（2）几个重要的对数恒等式: log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数：常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么 ①加法：log log log ()a a a M N MN += ②减法：log log log a a a M M N N -= ③数乘： log log ()n a a n M M n R =∈ ④log a N a N = ⑤log log (0,)b n a a n M M b n R b =≠∈ ⑥换底公式：log log (0,1)log b a b N N b b a = >≠且

复变函数考试试题与答案各种总结

《复变函数》考试试题（一）一、判断题（20分）： 1.若f(z)在z 0的某个邻域内可导，则函数f(z)在z 0解析. ( ) 2.有界整函数必在整个复平面为常数. ( ) 3.若 } {n z 收敛，则 } {Re n z 与 } {Im n z 都收敛. ( ) 4.若f(z)在区域D 内解析，且 0)('≡z f ，则C z f ≡)(（常数）. ( ) 5.若函数f(z)在z 0处解析，则它在该点的某个邻域内可以展开为幂级数. ( ) 6.若z 0是)(z f 的m 阶零点，则z 0是1/)(z f 的m 阶极点. ( ) 7.若 ) (lim 0 z f z z →存在且有限，则z 0是函数f(z)的可去奇点. ( ) 8.若函数f(z)在是区域D 内的单叶函数，则)(0)('D z z f ∈?≠. ( ) 9. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=? C dz z f . ( ) 10.若函数f(z)在区域D 内的某个圆内恒等于常数，则f(z)在区域D 内恒等于常数.（）二.填空题（20分） 1、 =-?=-1||0 0)(z z n z z dz __________.（n 为自然数） 2. =+z z 22cos sin _________. 3.函数z sin 的周期为___________. 4.设 11 )(2+= z z f ，则)(z f 的孤立奇点有__________. 5.幂级数 n n nz ∞ =∑的收敛半径为__________. 6.若函数f(z)在整个平面上处处解析，则称它是__________. 7.若ξ =∞ →n n z lim ，则= +++∞→n z z z n n (i) 21______________. = )0,(Re n z z e s ，其中n 为自然数.

人体寄生虫总结(详尽)

保虫宿主（reserboir host）:有些寄生虫即可寄生于人也可寄生于脊椎动物，脊椎动物体内的寄生虫在一定条件下可传给人，从流行病学角度上看，这些动物称保虫宿主。（例子：日本血吸虫的保虫宿主为牛、羊、鼠）。幼虫移行症（larva migrans）一些蠕虫侵入非正常宿主人后，不能发育为成虫，长期以幼虫状态存在，在皮下，组织，器官间窜扰，造成的局部或全身病变；分为内脏幼虫移行症和皮肤幼虫移行症；其共同特征是嗜酸性粒细胞增多，血中丙球蛋白及IgE水平升高。变态（metamorphosis）：昆虫从幼虫到成虫性成熟的过程中发生的外部形态、内部结构、生理功能到生态习性、行为的一系列变化。全变态(complete metamorphosis)：昆虫在个体发育中,经过卵、幼虫、蛹和成虫等4个时期地叫完全变态。不完全变态(Hemimetabolism)：昆虫发育过程不需要经历蛹期。世代交替（alternation of generation）：需要有性生殖与无性生殖交替进行才能完成生活史的现象。中间宿主．．．．（intermediate host）：指寄生虫的幼虫或无性生殖阶段所寄生的宿主。保虫宿主．．．．（reservoir host）亦称储存宿主，指某些寄生虫既可寄生于人，也可寄生于脊椎动物，后者在一定条件下可将体内的寄生虫传播给人。在流行病学上将这些脊椎动物称之为储存宿主或保虫宿主。转续宿主（．．．．． paratenic host ）有些寄生虫幼虫侵入非适宜宿主后不能发育成虫，但能存活并长期维持幼虫状态，只有当该幼虫有机会进入其适宜宿主体内时，才能发育为成虫。这种非适宜的宿主称为～。机会致病寄生虫．．．．．．．(opportunistic parasite)：某些寄生虫在宿主免疫功能正常时处于隐性感染状态，当宿主免疫功能低下时，虫体出现异常繁殖、致病力增强，导致宿主出现临床症状，称之。如弓形虫、微小隐孢子虫。共栖 ( commensalism )：两种不同的生物共同生活，其中一方受益，另一方既不受益，也不受害，此种现象称为共栖。鮣鱼与鲨鱼，海葵与寄居蟹。互利共生( mutualism ) ：两种生物共同生活，双方互相依靠，彼此受益，称为互利共生。河马与小鸟。寄生．．(parasitism)：两种生物共同生活，其中一方受益，另一方受害，受害者提供营养和居住场所给受益者，这种关系称为寄生。受益者称为寄生物(parasite)，受害者称为宿主(host)。。机会致病性寄生虫：某些寄生虫在健康的人体内寄生时，通常不表现明显致病性，但当人体免疫功能低下或缺陷时，则可出现异常增殖且致病力明显增强，引起人体急性感染或严重发作，甚至死亡。这类寄生虫称为机会致病性寄生虫。寄生虫生活史．．．．．．：是指寄生虫完成一代的生长、发育与繁殖的整个过程。包括寄生虫侵入宿主的途径、虫体在宿主体内移行、定居及离开宿主的方式，以及发育过程中所需的宿主种类（包括传播媒介）和内外环境条件等。我国五大寄生虫病：血吸虫病、疟疾、丝虫病、钩虫病、黑热病。寄生虫对宿主的损害：1、掠夺营养2、机械性损伤3、毒性与免疫损伤。宿主对寄生虫的抵抗：1、全部清除寄生虫，并具有抵御再感染能力。2、部分清除寄生虫，并具有部分抵御再感染能力。3、不能有效控制寄生虫，寄生虫发育并大量繁殖。导致寄生虫病。寄生虫感染．．．．．(．parasitic infection)：寄生虫侵入人体并能生活或长或短一段时间，若不引起明显的临床表现，这种现象称为寄生虫感染。有明显临床表现的寄生虫感染则称为寄生虫病。感染阶段(infection stage)：寄生虫生活史中能使人体感染的阶段，又称感染期。异位寄生．．．．(ectopic parasitism)：有些寄生虫在常见寄生部位以外的器官、组织内寄生,这种寄生现象称为异位寄生。人兽共患寄生虫病(parasitic zoonoses)：有些人体寄生虫病可以在人与动物之间自然的传播，这些寄生虫病称之。人兽共患寄生虫病主要有黑热病、弓形虫病、血吸虫病、肺吸虫病、肝吸虫病、姜片虫病、囊虫病、包虫病、曼氏迭宫绦虫裂头蚴病、旋毛虫病和广州管圆线虫等。自然疫源性：不需要人的参与而存在于自然界的人兽共患寄生虫病具有明显的自然疫源性。伴随免疫（concomitant immunity）：宿主感染蠕虫后对再感染产生不同程度的抵抗力，这种免疫力能作用于再次感染的幼虫或童虫，而对初次感染的成虫无杀伤作用，这种不完全非消除性免疫称伴随免疫，如血吸虫。终宿主（definitive host）:成虫或有性生殖阶段所寄生的宿主。