函数概念与基本初等函数典型例题解析

第二章 函数概念与基本初等函数 §2.1 映射、函数、反函数 7/16/2012

二、疑难知识导析 1.对映射概念的认识

(1) 与 是不同的，即 与 上有序的.或者说：映射是有方向的，

(2) 输出值的集合是集合B 的子集.即集合B 中可能有元素在集合A 中找不到对应的输入值.集合A 中每一个输入值，在集合B 中必定存在唯一的输出值.或者说：允许集合B 中有剩留元素；允许多对一，不允许一对多. (3)集合A ，B 可以是数集，也可以是点集或其它类型的集合. 2.对函数概念的认识

(2)注意定义中的集合 A ，B 都是非空的数集,而不能是其他集合； （3）函数的三种表示法：解析法，列表法，和图像法. 3.对反函数概念的认识 （1）函数y=

()f x 只有满足是从定义域到值域上一一映射，才有反函数；

（2）反函数的定义域和值域分别是原函数的值域和定义域，因此反函数的定义域一般不能由其解析式来求，而应该通过原函数的值域而得.

（3）互为反函数的函数有相同的单调性，它们的图像关于y=x 对称. 三、经典例题导讲

[例1]设M ＝｛a ，b ，c ｝，N ＝｛－2,0,2｝,求（1）从M 到N 的映射种数； （2）从M 到N 的映射满足 f

(a)>

f

(b)≥f(c),试确定这样的映射

f

的种数.

[例2]已知函数

()f x 的定义域为[0，1]，求函数(1)f x +的定义域

[例3]已知：*

,x N

∈5

(6)()(2)

(6)

x x f x f x x -≥?=?

+

(3)f .

[例4]已知

()f x 的反函数是1()f x -，如果()f x 与1()f x -的图像有交点，那么交点必在直线y x =上，判断此命题是否正确？

116

1()log 16x y y x ==与的图像的交点中，点1111(,),2442（，）

不在直线y x =上，由此可以说明“两互为反函数图像的交点必在直线

y x =上”是不正确的.

[例5]求函数2()46y f x x x ==-+，[1,5)x ∈的值域.

[例6]已知

()34f x x =+，求函数1(1)f x -+的解析式.

[例7]根据条件求下列各函数的解析式： （1）已知

()f x 是二次函数，若(0)0,(1)()1f f x f x x =+=++，求()f x .

（2）已知(1)2f x x x +=+

，求()

f x （3）若

()f x 满足1

()2(),f x f ax x

+=求()

f x

[例9]设

()f x 是R 上的函数，且满足(0)1,f =并且对任意的实数,x y 都有

()()(21)f x y f x y x y -=--+，求()f x 的表达式.

四、典型习题导练

1. 已知函数f(x)，x ∈F ，那么集合{(x ，y)|y=f(x)，x ∈F}∩{(x ，y)|x=1｝中所含元素的个数是（ ） A.0 B.1 C.0或1 D.1或2

2.对函数

b ax x x f ++=23)(作代换x =g(t)，则总不改变f (x )值域的代换是( )

A.t t g 2

1log )

(=

B.t t g )2

1()

(=

C.g(t)=(t －1)2

D.g(t)=cost

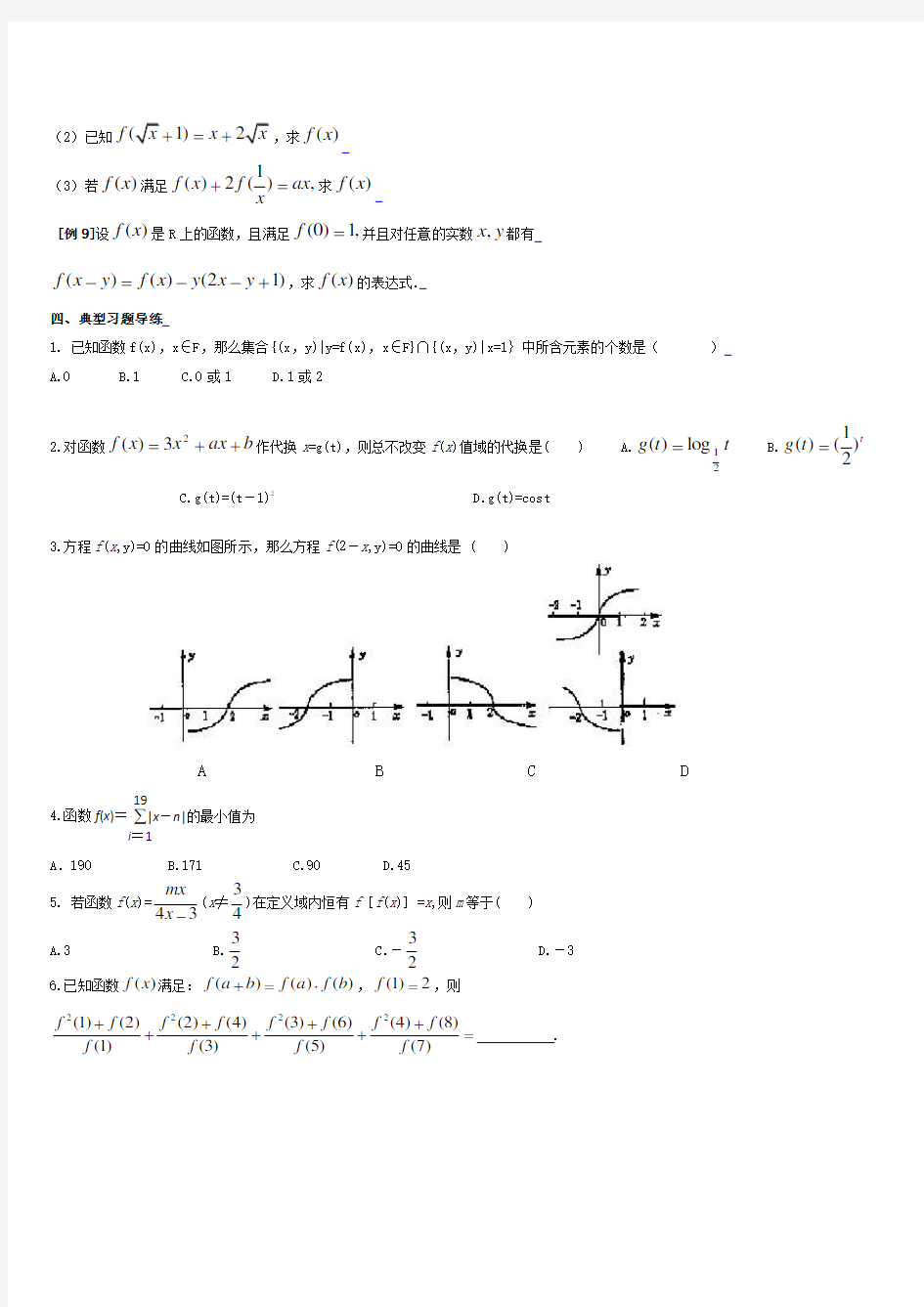
3.方程f (x ,y)=0的曲线如图所示，那么方程f (2－x ,y)=0的曲线是 ( )

4.函数f (x )＝∑i ＝1

19

|x －n |的最小值为

A ．190 B.171 C.90 D.45

5. 若函数f (x )=

34-x mx (x ≠4

3

)在定义域内恒有f ［f (x )］=x ,则m 等于( )

A.3

B.23

C.－2

3

D.－3

6.已知函数()f x 满足：()()()f a b f a f b +=?，(1)2f =，则

2222(1)(2)(2)(4)(3)(6)(4)(8)

(1)(3)(5)(7)

f f f f f f f f f f f f +++++++= .

A B C D

§2.2函数的性质

三、经典例题导讲 [例1]判断函数

1

()3

x y -=的单调性.

[例2]判断函数

1()(1)

1x f x x x

-=++的奇偶性. [定义域]

[例3] 判断

22()log (1)f x x x =++的奇偶性.

[例4]函数y=

2

45x x --的单调增区间是_________.

[例5] 已知奇函数f (x )是定义在(－3，3)上的减函数，且满足不等式f (x －3)+f (x 2

－3)<0,求x 的取值范围.

A ={x |2

[例7]若f(x)=

2

1

++x ax 在区间（－2，＋∞）上是增函数，求a 的取值范围

a ＞

2

1 [例8] 已知函数f (x )在(－1，1)上有定义，f (2

1

)=－1,当且仅当0

试证明：

(1)f (x )为奇函数；(2)f (x )在(－1，1)上单调递减 四、典型习题导练

1.某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了，再走余下的路，下图中y 轴表示离学校的距离，x 轴表示出发后的时间，则适合题意的图形是( )

2. 若函数)(x f 是定义在R 上的偶函数，在 ]0,(-∞上是减函数，且(2)0f = ，则使得x x f 的0)(<的取值范围是

（ ）

A.)2,(-∞

B. ),2(+∞

C. ),2()2,(+∞--∞

D.（－2，2）

3. 若函数)2(log )(22a x x x f n ++=是奇函数，则a = .

4. 已知

)(x f y =是定义在R 上的单调函数，实数21x x ≠，

,1,121λλλ++=

-≠x x a λ

λβ++=11

2

x x ，若|)()(||)()(|21βαf f x f x f -<-，则（ ）

A.0<λ

B.0=λ

C.10<<λ

D.1≥λ.

5.已知()f x 是定义在R 上的奇函数，且当(0,)x ∈+∞时，()f x

＝(1x +，求()f x .

§2.3 基本初等函数

一、知识导学 1.

二次函数的概念、图像和性质.

（1）注意解题中灵活运用二次函数的一般式2()(0)f x ax bx c a =++≠

二次函数的顶点式2()()(0)f x a x m n a =-+≠和

二次函数的坐标式

12()()()

(0)f x a x x x x a =--≠

2.指数函数

x y a =(0,1)a a >≠和对数函数log a y x =(0,1)a a >≠的概念和性质.

（1）有理指数幂的意义、幂的运算法则： ①m

n m n a

a a +?=；②()m n mn a a =；③()n n n a

b a b =（这时m,n 是有理数）

对数的概念及其运算性质、换底公式.

log ()log log ;

log log log a a a a

a a M

M N M N M N N

?=+=-

1

log log ;

log log n a a a a M n M M n

==

；

log log log c a c b

b a

=

二、疑难知识导析 （1

a ，

6.幂函数

y x α=的性质，要注意α

的取值变化对函数性质的影响.

（1）当奇奇=

α时，幂函数是奇函数；（2）当奇偶=α时，幂函数是偶函数；（3）当偶

奇=α时，定义域不关于原点对称，幂函数为非奇非偶函数.

三、经典例题导讲 [例1]已知18

log 9,185,b a ==求36log 45

1818183621818181818log 45log 5log 9

log 451818log 36log 4log 9

2log ()2log ()99

b a b a b a

a a a

++++=

==

==+-++

[例2]分析方程

2()0f x ax bx c =++=（0a >）的两个根都大于1的充要条件.

[例3]求函数

361265x x y =-?-的单调区间.

单调递减区间是(,1]-∞，单调递增区间为[1,)+∞

[例4]已知

)2(log ax y a -=在[0，1]上是x 的减函数，则a 的取值范围是

1＜a ＜2

[例5]已知函数

()log (3)a f x ax =-.

（1）当[0,2]x ∈时()f x 恒有意义，求实数a 的取值范围.

（2）是否存在这样的实数a 使得函数()f x 在区间[1，2]上为减函数，并且最大值为1，如果存在，试求出a 的值；如果不存在，请说明

理由.

[例6]已知函数f (x )=1

421lg 2+-?++a a a

x x , 其中a 为常数，若当x ∈(－∞, 1］时, f (x )有意义，求实数a 的取值范围.

分析：参数深含在一个复杂的复合函数的表达式中，欲直接建立关于a 的不等式（组）非常困难，故应转换思维角度，设法从原式中把a 分离出来，重新认识a 与其它变元(x )的依存关系，利用新的函数关系，常可使原问题“柳暗花明”.

解：

1

4212+-?++a a a x x >0, 且a 2

－a +1=(a －

21)2

+4

3

>0, ∴ 1+2x

+4x

·a >0, a >)2141(

x x +-, 当x ∈(－∞, 1]时, y =x 41与y =x 2

1

都是减函数，

∴ y =)2141(x x +-在(－∞, 1]上是增函数，)2

1

41(x x +-max =－43,

∴ a >－43, 故a 的取值范围是(－4

3

, +∞).

点评：发掘、提炼多变元问题中变元间的相互依存、相互制约的关系、反客为主，主客换位，创设新的函数，并利用新函数的性质创造性地使原问题获解，是解题人思维品质高的表现.本题主客换位后，利用新建函数y =)21

41(x

x +-的单调性转换为函数最值巧妙地求出了实数a 的取值范围.此法也叫主元法. 四、典型习题导练 1. 函数b x a x f -=)(的图像如图，其中a 、b 为常数，则下列结论正确的是（ ）

A.0,1<>b a

B.0,1>>b a

C.0,10><<

b a D.0,10<<<

b a

2、已知2lg(x －2y)=lgx+lgy,则y

x 的值为（ ） A.1 B.4

C.1或4

D.4 或 8

3、方程2)1(log 2=++x x a (0

A.0

B.1

C.2

D.3

4、函数f(x)与g(x)=(2

1

)x

的图像关于直线y=x 对称,则f(4－x 2

)的单调递增区间是 ( ）

A.

[)+∞,0 B.

(]0,∞-

C.

[)2,0 D.

(]0,2-

5、图中曲线是幂函数y ＝x n

在第一象限的图像，已知n 可取±2，±12

四个值,则相应于曲线c1、

c2、c3、c4的n 依次为( ) A.－2，－12，12，2 B ．2，12，－1

2

，－2 C. －

12，－2,2，12 D. 2，12，－2, －12

6. 求函数y = log 2 (x 2

－5x+6) 的定义域、值域、单调区间. 7. 若x 满足03log 14)(log 2422

1

≤+-x x ,求

f(x)=2

log 2

log 2

2

x x

最大值和最小

值.

8.已知定义在R 上的函数()2,2

x x a

f x =+

a 为常数 （1）如果()f x ＝()f x -，求a 的值；

（2）当

()f x 满足（1）时，用单调性定义讨论()f x 的单调性.

§2.4 函数与方程

一、知识导学

1.函数的零点与方程的根的关系： 一般地，对于函数

()y f x =（x D ∈）我们称方程()0f x =的实数根x 也叫做函数的零点，即函数的零点就是使函数值为零的自

变量的值. 求综合方程f (x )=g (x )的根或根的个数就是求函数()()y f x g x =-的零点.

2.函数的图像与方程的根的关系： 一般地，函数

()y f x =（x D ∈）的图像与x 轴交点的横坐标就是()0f x =的根.综合方程f (x )=g (x )的根，就是求函数y ＝f (x )

与y =g (x )的图像的交点或交点个数，或求方程()()y f x g x =-的图像与x 轴交点的横坐标.

3.判断一个函数是否有零点的方法： 如果函数

()y f x =在区间[a,b]上图像是连续不断的曲线，并且有()()0f a f b ?<，那么，函数()y f x =在区间（a,b ）上至少

有一个零点，即至少存在一个数(,)c a b ∈使得

()0f c =，这个c 也就是方程()0f x =的一个根.对于我们学习的简单函数，可以借助

()y f x =图像判断解的个数，或者把()f x 写成()()g x h x -，然后借助()y g x =、()y h x =的图像的交点去判断函数()f x 的零

点情况.

4. 二次函数、一元二次方程、二次函数图像之间的关系： 二次函数2y ax bx c =++的零点，就是二次方程20ax bx c ++=的根，也是二次函数2y ax bx c =++的图像与

x 轴交点的

横坐标. 5. 二分法：

对于区间[a,b]上的连续不断，且

()()0f a f b ?<的函数()y f x =，通过不断地把函数的零点所在的区间一分为二，使区间的两

个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法. 三、经典例题导讲 [例1]已知函数2()3f x x ax a =++-若[2,2]x ∈-时，()f x ≥0恒成立，求a 的取值范围.

综上，得－7≤a ≤2 [例2]已知2

10mx x ++=有且只有一根在区间（0,1）内，求m 的取值范围.

综上所得，m ＜－2 四、典型习题导练 1. 方程023

=-+x x

的实根的个数是（

）

A. 0

B. 1

C. 2

D. 3.

2.已知抛物线

2()27y f x x mx m ==++-与x 轴的两个交点在（1,0）两旁，则关于x 的方程221

(1)504

x m x m ++++=的根

的情况是（ ）

Ａ.有两个正数根 B.有两个负数根 C.有一个正数根和一个负数根 D.无实数根 3.若关于x 的方程2

210ax

x --=在（0,1）内恰有一解，则a 的取值范围为（

）

A. a ＜－1

B. a ＞1

C. －1＜a ＜1

D.0＜a ＜1

4.已知函数

d cx bx ax x f +++=23)(的图像如图所示，则b 的取值范围是（

）

A.(-∞,0)

B.(0,1)

C.(1,2)

D.(2,+∞) 5.已知函数

=y )(x f 对一切实数都有)2()2(x f x f -=+成立，

且方程)(x f =0恰有6个不同的实根，则这6个根的和是 . 6. 已知在二次函数的解析式2()f x ax bx c =++中，(1)f ＝－3，(0)f ＝－8，且它的两个零点间的距离等于2，求这个二次函数的

解析式.

§2.5 函数的综合运用

三、经典例题导讲 [例1] 不等式 ).23(log )423(log 2

)

2(2)2(22

+->--++x x x x x x

[例5] 定义在R 上的函数()f x 满足：对任意实数,m n ，总有()()()f m n f m f n +=?，且当0x >时，()01f x <<.

（1）试求()0f 的值；

（2）判断

()f x 的单调性并证明你的结论；

解：（1）在()()()f m n f m f n +=?中，令1,0m n ==.得：()()()110f f f =?.

因为

()10f ≠，所以，()01f =.

（2）要判断()f x 的单调性，可任取12,x x R ∈，且设12x x <.

在已知条件()()()f m n f m f n +=?中，若取21,m n x m x +==，则已知条件可化为：()()()

2121f x f x f x x =?-.

由于210x x ->，所以()2110f x x >->.

为比较()()21f x f x 、的大小，只需考虑()1f x 的正负即可.

在

()()()f m n f m f n +=?中，令m x =，n x =-，则得()()1f x f x ?-=. ∵ 0x

>时，()01f x <<，

∴ 当0x <时，

()()

1

10f x f x =

>>-.

又

()01f =，所以，综上，可知，对于任意1x R ∈，均有()10f x >.

∴

()()()()2112110f x f x f x f x x -=--

∴ 函数

()f x 在R 上单调递减.

[例6]设a 为实数，函数1||)(2+-+=a x x x f ，R x ∈

（1）讨论)(x f 的奇偶性；

（2）求

)(x f 的最小值.

解：（1）当0=a 时，函数)(1||)()(2x f x x x f =+-+-=-

此时，)(x f 为偶函数

当0≠a

时，1)(2+=a a f ，1||2)(2++=-a a a f ，

)()(a f a f -≠，)()(a f a f --≠

此时

)(x f 既不是奇函数，也不是偶函数

（2）（i ）当a x ≤时，4

3

)21(1)(22++-=++-=a x a x x x f

当21≤

a

，则函数)(x f 在],(a -∞上单调递减，从而函数)(x f 在],(a -∞上的最小值为1)(2

+=a a f . 若21>a ，则函数)(x f 在],(a -∞上的最小值为a f +=43)21(，且)()2

1

(a f f ≤.

（ii ）当a x ≥时，函数4

3)21(1)(22

+-+=+-+=a x a x x x f

若21-≤a ，则函数)(x f 在],(a -∞上的最小值为a f -=-43)21(，且)()21

(a f f ≤-

若2

1->a ，则函数)(x f 在),[+∞a 上单调递增，从而函数)(x f 在),[+∞a 上的最小值为1)(2

+=a a f .

综上，当21-≤a 时，函数)(x f 的最小值为a -4

3

当2121≤<-a 时，函数)(x f 的最小值为12

+a

当21>a 时，函数)(x f 的最小值为a +4

3

.

四、典型习题导练 1.对函数

b ax x x f ++=23)(作代换x =g(t)，则总不改变f (x )值域的代换是 ( )

A.t t g 2

1log )

(=

B.t t g )2

1

()

(=

C.g(t)=(t －1)2

D.g(t)=cost

2.用铁管做一个形状为直角三角形的铁框架，要使直角三角形面积为1平方米，有下列四种长度的铁管，最合理（够用，浪费又最少）的是（ ）

A.4.1米

B.4.8米

C.5米

D.5.2米 3.函数|1|||ln --=x e y x 的图像大致是（ ）

4.设x 1、x 2为方程4x 2

－4mx +m +2=0的两个实根，当m =_________时，x 12

+x 22

有最小值_________.