高等数学(同济版)上册第六章简明答案

习题6-2
1. 求图6-21 中各画斜线部分的面积:
(1)
解 画斜线部分在x 轴上的投影区间为[0, 1]. 所求的面积为
6
1]2132[)(102231
0=-=-=?x x dx x x A .
(2)
解法一 画斜线部分在x 轴上的投影区间为[0, 1]. 所求的面积为
1|)()(101
0=-=-=?x x e ex dx e e A ,
解法二 画斜线部分在y 轴上的投影区间为[1, e ]. 所求的面积为
1)1(|ln ln 1
11=--=-==??e e dy y y ydy A e
e e
.
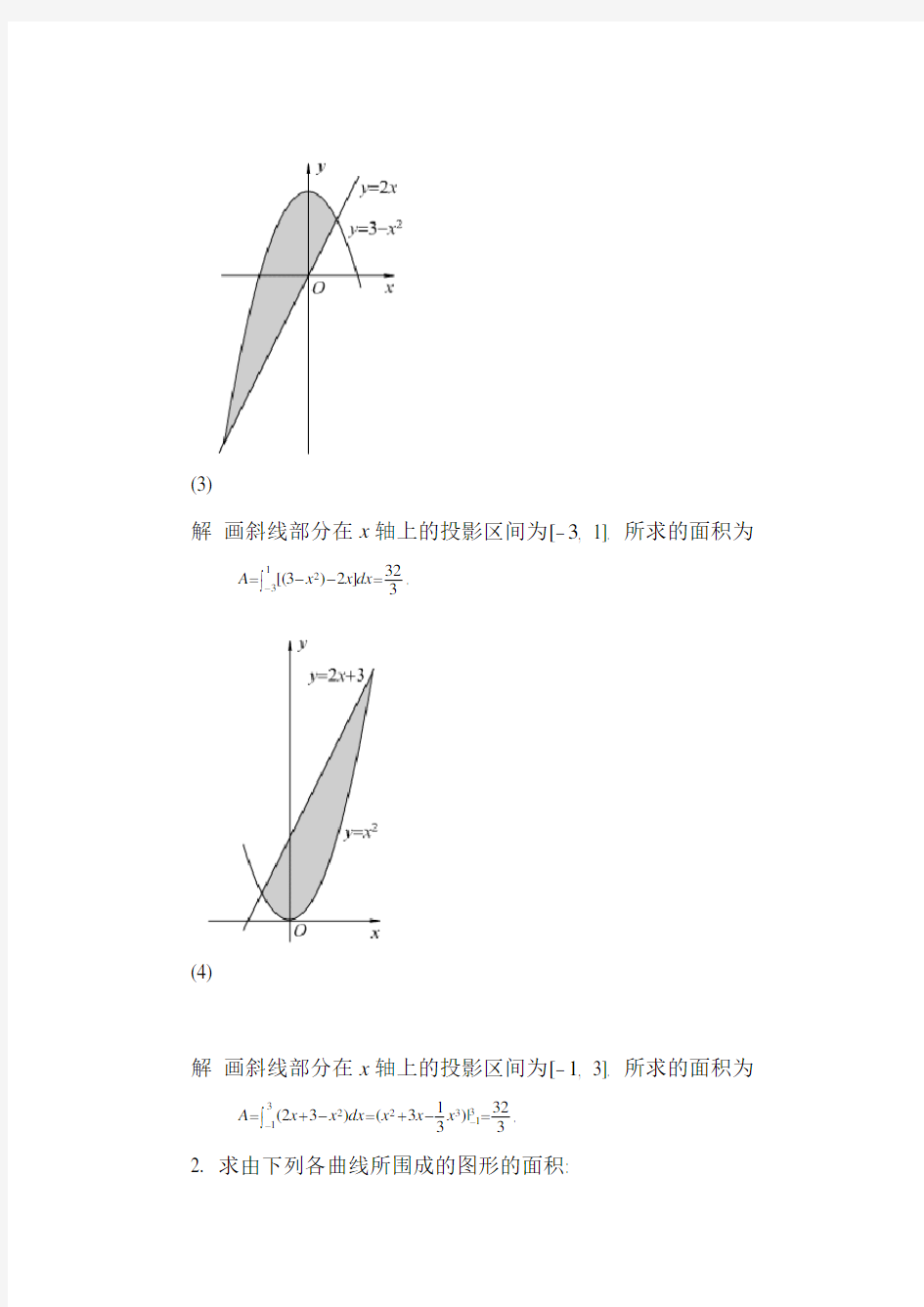
(3)
解 画斜线部分在x 轴上的投影区间为[-3, 1]. 所求的面积为
3
32]2)3[(1
32=--=?-dx x x A .
(4)
解 画斜线部分在x 轴上的投影区间为[-1, 3]. 所求的面积为
3
32|)313()32(31323
12=-+=-+=--?x x x dx x x A .
2. 求由下列各曲线所围成的图形的面积:
(1)
22
1x y =与x 2+y 2=8(两部分都要计算);
解:
3
88282)218(22
0220220220221--=--=--=????dx x dx x dx x dx x x A
3
4238cos 16402+=-=?ππ
tdt .
3
46)22(122-=-=ππS A . (2)x
y 1=与直线y =x 及x =2;
解: 所求的面积为
?-=-=2
12ln 2
3)1(dx x x A .
(3) y =e x , y =e -x 与直线x =1;
解:
所求的面积为
?-+=-=-1
21)(e
e dx e e A x x . (4)y =ln x , y 轴与直线y =ln a , y =ln b (b >a >0).
解
所求的面积为
a b e dy e A b
a y b
a y -===?ln ln ln ln 3. 求抛物线y =-x 2+4x -3及其在点(0, -3)和(3, 0)处的切线所围成的图形的面积. 解:
y '=-2 x +4.
过点(0, -3)处的切线的斜率为4, 切线方程为y =4(x -3). 过点(3, 0)处的切线的斜率为-2, 切线方程为y =-2x +6.
两切线的交点为)3 ,2
3(, 所求的面积为
49]34(62[)]34(34[23023
2
32=-+--+-+-+---=?
?
dx x x x x x x A .
4. 求抛物线y 2=2px 及其在点),2
(p p 处的法线所围成的图形的面积
. 解 2y ?y '=2p . 在点),2
(p p 处,
1)
,2(==
'p p y p
y , 法线的斜率k =-1,
法线的方程为)2
(p x p y --=-, 即y p x -=2
3.
求得法线与抛物线的两个交点为),2
(p p 和)3,2
9(p p -.
法线与抛物线所围成的图形的面积为
2332323
16)612123()223(p y p y y p dy p y y p A p
p
p
p =--=--=--?.
5. 求由下列各曲线 所围成的图形的面积; (1)ρ=2a cos θ ;
解: 所求的面积为
??==-202222
2cos 4)cos 2(21π
π
πθθθθd a d a A =πa 2.
(2)x =a cos 3t , y =a sin 3t ;
解 所求的面积为
???===204220
2
330sin cos 34)cos ()sin (44π
πtdt t a t a d t a ydx A a
2060428
3]sin sin [12a tdt tdt a ππ
π=-=??.
(3)ρ=2a (2+cos θ )
解
所求的面积为
2202220218)cos cos 44(2)]cos 2(2[2
1a d a d a A πθθθθθπ
π=++=+=??.
6. 求由摆线x =a (t -sin t ), y =a (1-cos t )的一拱(0≤t ≤2π)与横轴 所围
成的图形的面积. 解:
所求的面积为 ???-=--==a
a a dt t a dt t a t a ydx A 20222020)cos 1()cos 1()cos 1(π
π
22023)2
cos 1cos 21(a dt t t a a
=++-=?.
7. 求对数螺线ρ=ae θ(-π≤θ≤π)及射线θ=π所围成的图形面积.
解
所求的面积为
)(4
21)(21222222πππ
πθππθθθ----===??e e a d e a d ae A .
8. 求下列各曲线所围成图形的公共部分的面积. (1)ρ=3cos θ 及ρ=1+cos θ 解
曲线ρ=3cos θ 与ρ=1+cos θ 交点的极坐标为)3
,23(πA , )3
,2
3(π-B . 由对
称性, 所求的面积为
π
θθθθπ
ππ4
5])cos 3(21)cos 1(21[2202=++=??d d A .
(2)θ
ρsin 2=
及θρ2cos 2=.
解 曲线θ
ρsin 2=与θρ2cos 2=的交点M 的极坐标为M )6
,22(
π.
所求的面
积为 2
3
16]2c o s 21)sin 2(21[246602-+=+=??πθθθθπ
ππd d A .
9. 求位于曲线y =e x 下方, 该曲线过原点的切线的左方以及x 轴上方之间的图形的面积.
解 设直线y =kx 与曲线y =e x 相切于A (x 0, y 0)点, 则有 ???
??=='==k
e x y e y kx y x x 00)(0000,
求得x 0=1, y 0=e , k =e . 所求面积为
2
1ln 21)ln 1(00020e dy y y y y y e dy y y e e e e
e
=?+-=-??.
10. 求由抛物线y 2=4ax 与过焦点的弦所围成的图形的面积的最小值. 解 设弦的倾角为α. 由图可以看出, 抛物线与过焦点的弦所围成的图形的面积为 10A A A +=.
显然当2
πα=时, A 1=0; 当2πα<时, A 1>0.
因此, 抛物线与过焦点的弦所围成的图形的面积的最小值为 203
03
83822a x a dx ax A a a
===?
.
11. 把抛物线y 2=4ax 及直线x =x 0(x 0>0)所围成的图形绕x 轴旋转, 计算所得旋转体的体积.
解 所得旋转体的体积为
2
0020
222400
x a x a axdx dx y V x
x x ππππ====??.
12. 由y =x 3, x =2, y =0所围成的图形, 分别绕x 轴及y
轴旋转, 计算所得两个旋转体的体积. 解 绕x 轴旋转所得旋转体的体积为 ππππ7
128712
072
062
02
====??x dx x dx y V x .
绕y 轴旋转所得旋转体的体积为 ??-=-??=8
3
2
8
22
3282dy y dy x V y ππππ
πππ5
6453328035=-=y . 13. 把星形线3/23/23/2a y x =+所围成的图形, 绕x 轴旋转, 计算所得旋转体的体积.
解 由对称性, 所求旋转体的体积为
dx x a dx y V a
a ??-==0
3
32320
2)(22ππ
3023
4323234
2
105
32)33(2a dx x x a x a a a
ππ=-+-=?.
14. 用积分方法证明图中球缺的体积为)3(2H R H V -=π.
证明 ?
?
---==R
H
R R H
R dy y R dy y x V )()(222
ππ
)3()31(232H R H y y R R
H R -=-=-ππ.
15. 求下列已知曲线所围成的图形, 按指定的轴旋转所产生的旋转体的体积:
(1)2x y =, 2y x =, 绕y 轴;
解 ππππ10
3)5121()(1
0521
0221
0=-=-=??y y dy y ydy V .
(2)a
x a y ch =, x =0, x =a , y =0, 绕x 轴; 解 ???===102302
2
02
ch ch )(udu a au x dx a
x a dx x y V a
a
πππ令
10
22310
223)2
1221(4)2(4
u u u
u e u e a du e e a ---+=++=?ππ )2sh 2(4
3
+=
a π. (3)16)5(22=-+y x , 绕x 轴.
解 ??
------+=4
4
224
4
2
2)165()165(dx x dx x V ππ
24
21601640π?=-=dx x .
(4)摆线x =a (t -sin t ), y =a (1-cos t )的一拱, y =0, 绕直线y =2a . 解 ??--=π
πππa a dx y a dx a V 202202)2()2( ?----=π
ππ20223)sin ()]cos 1(2[8t t da t a a a
232023237sin )cos 1(8ππππa tdt t a a =+-=?. 16. 求圆盘222a y x ≤+绕x =-b (b >a >0)旋转所成旋转体的体积.
解 ??------+=a
a
a
a
dy y a b dy y a b V 2222
22
)()(ππ
22
2228ππb a dy y a b a
=-=?
.
17. 设有一截锥体, 其高为h , 上、下底均为椭圆, 椭圆的轴长分别为2a 、2b 和2A 、2B , 求这截锥体的体积.
解 建立坐标系如图. 过y 轴上y 点作垂直于
y 轴的平面, 则平面与截锥体的截面为椭圆, 易得其长短半轴分别为
y h a A A --, y h b B B --.
截面的面积为π)()(y h b B B y h a A A --?--.
于是截锥体的体积为
])(2[6
1)()(0bA aB AB ab h dy y h b B B y h a A A V h
+++=--?--=?ππ. 18. 计算底面是半径为R 的圆, 而垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积.
解 设过点x 且垂直于x 轴的截面面积为A (x ), 由已知条件知, 它是边长为x R -2的等边三角形的面积, 其值为
)(3)(22x R x A -=, 所以 3223
34)(3R dx x R V R
R
=-=?
-.
19. 证明 由平面图形0≤a ≤x ≤b , 0≤y ≤f (x )绕y 轴旋转所成的旋转体的体积为
?=b
a dx x xf V )(2π.
证明 如图, 在x 处取一宽为dx 的小曲边梯形, 小曲边梯形绕y
轴旋转所得的旋转体的体积近似为2πx ?f (x )dx , 这就是体积元素, 即 dV =2πx ?f (x )dx ,
于是平面图形绕y 轴旋转所成的旋转体的体积为 ??==b
a
b
a
dx x xf dx x xf V )(2)(2ππ.
20. 利用题19和结论, 计算曲线y =sin x (0≤x ≤π)和x 轴所围成的图形绕y 轴旋转所得旋转体的体积.
解 200
2)sin cos (2cos 2sin 2πππππ
π
π=+-=-==??x x x x xd xdx x V .
21. 计算曲线y =ln x 上相应于83≤≤x 的一段弧的长度. 解 ??
?
+=+='+=83283
2
83
2
1)1(1)(1dx x
x dx x dx x y s ,
令t x =+21, 即12-=t x , 则 23ln 2111111
1322323
222232
2+=-+=-=-?-=????
dt t dt dt t t dt t t
t t s .
22. 计算曲线)3(3x x y -=上相应于
1≤x ≤3的一段弧的长度.
解 x x x y 31-=, x x y 2121-=',
x x y 4121412+-=', )1(2112x x y +='+, 所求弧长为
3432)232(21)1(213
131-=+=+=?x x x dx x
x s .
23. 计算半立方抛物线32)1(32-=x y 被抛物线32x y =截得的一段弧
的长度.
解 由??
???=-=3)1(3223
2x y x y 得两曲线的交点的坐标为)36 ,2(, )36 ,2(-.
所求弧长为?'+=2
1
212dx y s .
因为
2
)1(22-='x y y , y
x y 2
)1(-=', )1(23)1(3
2)1()1(34242
-=--=-=
'x x x y x y . 所以 ]1)25[(98)13(13232)1(23122321
2
1
-=--=-+=??
x d x dx x s . 24. 计算抛物线y 2=2px 从顶点到这曲线上的一点M (x , y )的弧长. 解 ??
?
+=+='+=y y
y dy y p p dy p y dy y x s 0
220
20
2
1)(1)(1
y y p y p y p y p 022222])ln(2
2[1++++=
p
y p y p y p p y 222
2ln 22++++=. 25. 计算星形线t a x 3cos =, t a y 3sin =的全长.
解 用参数方程的弧长公式. dt t y t x s ?'+'=20
22)()(4π
??+-?=20
2222]cos sin 3[)]sin (cos 3[4π
dt t t a t t a
a tdt t 6cos sin 1220
==?π
.
26. 将绕在圆(半径为a )上的细线放开拉直, 使细线与圆周始终相切, 细线端点画出的轨迹叫做圆的渐伸线, 它的方程为 )sin (cos t t t a x +=, )cos (sin t t t a y -=.
计算这曲线上相应于t 从0变到π的一段弧的长度.
解 由参数方程弧长公式
?
?+='+'=π
π0
220
2
2
)sin ()cos ()]([)]([dt t at t at dt t y t x s
202
ππ
a tdt a ==?. 27. 在摆线x =a (t -sin t ), y =a (1-cos t )上求分摆线第一拱成1: 3的点的坐标.
解 设t 从0变化到t 0时摆线第一拱上对应的弧长为s (t 0), 则 ?
?
+-='+'=0
00
220
2
2
0]sin [)]cos 1([)]([)]([)(t t dt t a t a dt t y t x t s
)2
cos 1(42sin 2000t
a dt t a t -==?.
当t 0=2π时, 得第一拱弧长s (2π)=8a . 为求分摆线第一拱为1: 3的点为A (x , y ), 令
a t
a 2)2
cos 1(40=-,
解得3
20π=t , 因而分点的坐标为:
横坐标a a x )2332()32sin 32(-=-=πππ,
纵坐标a a y 23)32cos 1(=-=π,
故所求分点的坐标为)2
3 ,)2332((a a -π.
28. 求对数螺线θρa e =相应于自θ=0到θ=?的一段弧长. 解 用极坐标的弧长公式. θθθρθρ?
θθ?
d a
e e d s a a ?
?+='+=0
220
22
)()()()(
)1(112
2-+=+=?
θ?
θ
θa a e a
a d e a . 29. 求曲线ρθ=1相应于自43=θ至34=θ的一段弧长.
解 按极坐标公式可得所求的弧长 ?
?
-+='+=344
322234
4
32
2
)1()1()()(θθ
θθθρθρd d s
23ln 12511344
322+=+=?θθθd .
30. 求心形线ρ=a (1+cos θ )的全长. 解 用极坐标的弧长公式. θθθθθρθρπ
π
d a a d s ??
-++='+=0
2220
2
2
)sin ()cos 1(2)()(2
a d a 82
cos 40==?π
θθ.
习题6-3
1. 由实验知道, 弹簧在拉伸过程中, 需要的力F (单位: N )与伸长量s (单位: cm)成正比, 即F =ks (k 为比例常数). 如果把弹簧由原长拉伸6cm , 计算所作的功.
解 将弹簧一端固定于A , 另一端在自由长度时的点O 为坐标原点, 建立坐标系. 功元素为dW =ksds , 所求功为 182
16
026
0===?s k ksds W k(牛?厘米). 2. 直径为20cm 、高80cm 的圆柱体内充满压强为10N/cm 2的蒸汽. 设温度保持不变, 要使蒸汽体积缩小一半, 问需要作多少功? 解 由玻-马定律知:
ππ80000)8010(102=??==k PV .
设蒸气在圆柱体内变化时底面积不变, 高度减小x 厘米时压强 为P (x )牛/厘米2, 则
ππ80000)]80)(10[()(2=-?x x P , π-=80800)(x P .
功元素为dx x P dW )()10(2?=π,
所求功为 2ln 8008018000080800)10(40040
2
ππππ
π=-=-??=??
dx dx W (J). 3. (1)证明: 把质量为m 的物体从地球表面升高到h 处所作的功是
h
R mgRh
W +=
, 其中g 是地面上的重力加速度, R 是地球的半径;
(2)一颗人造地球卫星的质量为173kg , 在高于地面630km 处进入轨道. 问把这颗卫星从地面送到630的高空处, 克服地球引力要作多少功?已知g =9.8m/s 2, 地球半径R =6370km .
证明 (1)取地球中心为坐标原点, 把质量为m 的物体升高的功元素为
dy y kMm dW 2=,
所求的功为 )
(2h R R mMh k dy y kMm W h
R R
+?==?
+. (2)5333
2411
1075.910
)6306370(106370106301098.51731067.6?=?+???????=-W (kJ). 4. 一物体按规律3ct x =作直线运动, 媒质的阻力与速度的平方成正比. 计算物体由x =0移至x =a 时, 克服媒质阻力所作的功. 解 因为3ct x =, 所以
23)(cx t x v ='=, 阻力4
229t kc kv f -=-=. 而32)(c
x t =, 所以
3432342
9)(9)(x kc c
x kc x f -=-=. 功元素dW =-f (x )dx , 所求之功为 37
320
3
4320
3
43
20
7
2799)]([a kc dx x kc
dx x kc dx x f W a a
a
===-=?
??. 5. 用铁锤将一铁钉击入木板, 设木板对铁钉的阻力与铁钉击入木板的深度成正比, 在击第一次时, 将铁钉击入木板1cm . 如果铁锤每次打击铁钉所做的功相等, 问锤击第二次时, 铁钉又击入多少? 解 设锤击第二次时铁钉又击入h cm , 因木板对铁钉的阻力f 与铁钉击入木板的深度x (cm)成正比, 即f =kx , 功元素dW =f dx =kxdx , 击第一次作功为
k kxdx W 2
11
01==?,
击第二次作功为
)2(2
12112h h k kxdx W h
+==?+. 因为21W W =, 所以有 )2(21212h h k k +=, 解得12-=h (cm).
6. 设一锥形贮水池, 深15m , 口径20m , 盛满水, 今以唧筒将水吸尽, 问要作多少功?
解 在水深x 处, 水平截面半径为x r 3
210-=, 功元素为
dx x x dx r x dW 22)3210(-=?=ππ,
所求功为
?-=15
02)3
210(dx x x W π
?+-=15
032)9
440100(dx x x x π =1875(吨米)=57785.7(kJ).
7. 有一闸门, 它的形状和尺寸如图, 水面超过门顶2m . 求闸门上所受的水压力.
解 建立x 轴, 方向向下, 原点在水面. 水压力元素为
xdx dx x dP 221=??=, 闸门上所受的水压力为
2125
225
2===?x xdx P (吨)=205. 8(kN).
8. 洒水车上的水箱是一个横放的椭圆柱体, 尺寸如图所示. 当水箱装满水时, 计算水箱的一个端面所受的压力.
解 建立坐标系如图, 则椭圆的方程为 11)4
3()43(22
22=+-y x . 压力元素为
(完整版)同济大学高等数学上第七版教学大纲(64学时)
福建警察学院 《高等数学一》课程教学大纲 课程名称:高等数学一 课程编号: 学分:4 适用对象: 一、课程的地位、教学目标和基本要求 (一)课程地位 高等数学是各专业必修的一门重要的基础理论课程,它具有高度的抽象性、严密的逻辑性和应用的广泛性,对培养和提高学生的思维素质、创新能力、科学精神、治学态度以及用数学解决实际问题的能力都有着非常重要的作用。高等数学课程不仅仅是学习后继课程必不可少的基础,也是培养理性思维的重要载体,在培养学生数学素养、创新意识、创新精神和能力方面将会发挥其独特作用。 (二)教学目标 通过本课程的学习,逐步培养学生使其具有数学运算能力、抽象思维能力、空间想象能力、科学创新能力,尤其具有综合运用数学知识、数学方法结合所学专业知识去分析和解决实际问题的能力,一是为后继课程提供必需的基础数学知识;二是传授数学思想,培养学生的创新意识,逐步提高学生的数学素养、数学思维能力和应用数学的能力。 (三)基本要求 1、基本知识、基本理论方面:掌握理解极限和连续的基本概念及其应用;熟悉导数与微分的基本公式与运算法则;掌握中值定理及导数的应用;掌握不定积分的概念和积分方法;掌握定积分的概念与性质;掌握定积分在几何上的应用。 2、能力、技能培养方面:掌握一元微积分的基本概念、基本理论、基本运算技能和常用的数学方法,培养学生利用微积分解决实际问题的能力。
二、教学内容与要求 第一章函数与极限 【教学目的】 通过本章学习 1、理解函数的概念,了解函数的几种特性(有界性),掌握复合函数的概念及其分 解,掌握基本初等函数的性质及其图形,理解初等函数的概念。 2、理解数列极限的概念、掌握数列极限的证明方法、了解收敛数列的性质。 3、理解函数极限和单侧极限的概念,掌握函数极限的证明方法、理解极限存在与 左、右极限之间的关系,了解函数极限的性质。 4、理解无穷小和无穷大的概念、掌握无穷大和无穷小的证明方法。 5、掌握极限运算法则。 6、了解极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极 限的方法。 7、掌握无穷小的比较方法,会用等价无穷小求极限。 8、理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。 9、了解连续函数的运算和初等函数的连续性, 10、了解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理), 并会应用这些性质。 【教学重点与难点】 本章重点是求函数极限的方法(极限运算法则、两个重要极限、无穷小的比较、初等函数的连续性)。难点是数列、函数极限的证明方法。 【教学内容】 第一节映射与函数 一、映射 1.映射概念
高等数学(同济第七版)上册-知识点总结
高等数学(同济第七版)上册-知识点总结 第一章 函数与极限 一. 函数的概念 1.两个无穷小的比较 设0)(lim ,0)(lim ==x g x f 且l x g x f =) () (lim (1)l = 0,称f (x)是比g(x)高阶的无穷小,记以f (x) = 0[)(x g ],称g(x)是比f(x)低阶的无穷小。 (2)l ≠ 0,称f (x)与g(x)是同阶无穷小。 (3)l = 1,称f (x)与g(x)是等价无穷小,记以f (x) ~ g(x) 2.常见的等价无穷小 当x →0时 sin x ~ x ,tan x ~ x ,x arcsin ~ x ,x arccos ~ x , 1? cos x ~ 2/2^x , x e ?1 ~ x ,)1ln(x + ~ x ,1)1(-+αx ~ x α 二.求极限的方法 1.两个准则 准则 1. 单调有界数列极限一定存在 准则 2.(夹逼定理)设g (x ) ≤ f (x ) ≤ h (x ) 若A x h A x g ==)(lim ,)(lim ,则A x f =)(lim 2.两个重要公式 公式11sin lim 0=→x x x 公式2e x x x =+→/10 )1(lim 3.用无穷小重要性质和等价无穷小代换 4.用泰勒公式 当x 0→时,有以下公式,可当做等价无穷小更深层次 ) ()! 12()1(...!5!3sin ) (! ...!3!2112125332++++-+++-=++++++=n n n n n x x o n x x x x x x o n x x x x e )(! 2)1(...!4!21cos 2242n n n x o n x x x x +-+++-= )()1(...32)1ln(132n n n x o n x x x x x +-++-=++ )(! ))1()...(1(...!2)1(1)1(2n n x o x n n x x x +---++-++=+ααααααα )(1 2)1(...53arctan 121 2153+++++-+-+-=n n n x o n x x x x x 5.洛必达法则
(完整版)同济大学___高数上册知识点
高等数学上册复习要点 一、 函数与极限 (一) 函数 1、 函数定义及性质(有界性、单调性、奇偶性、周期性); 2、 反函数、复合函数、函数的运算; 3、 初等函数:幂函数、指数函数、对数函数、三角函数、反三角函数; 4、 函数的连续性与间断点; 函数)(x f 在 0x 连续 )()(lim 00 x f x f x x =→ 第一类:左右极限均存在. 间断点 可去间断点、跳跃间断点 第二类:左右极限、至少有一个不存在. 无穷间断点、振荡间断点 5、 闭区间上连续函数的性质:有界性与最大值最小值定理、零点定理、介值定 理及其推论. (二) 极限 1、 定义 1) 数列极限 εε<->?N ∈?>??=∞ →a x N n N a x n n n , , ,0lim 2) 函数极限 εδδε<-<-?>??=→A x f x x x A x f x x )( 0 , ,0 ,0)(lim 00 时,当 左极限:)(lim )(0 0x f x f x x - →-= 右极限:)(lim )(0 0x f x f x x +→+=
)()( )(lim 000 + -→=?=x f x f A x f x x 存在 2、 极限存在准则 1) 夹逼准则: 1))(0n n z x y n n n ≥≤≤ 2 ) a z y n n n n ==→∞ →∞ lim lim a x n n =∞ →lim 2) 单调有界准则:单调有界数列必有极限. 3、 无穷小(大)量 1) 定义:若0lim =α则称为无穷小量;若∞=αlim 则称为无穷大量. 2) 无穷小的阶:高阶无穷小、同阶无穷小、等价无穷小、k 阶无穷小 Th1 )(~ ααββαo +=?; Th2 αβαβαβββαα' ' =''''lim lim lim ,~,~存在,则(无穷小代换) 4、 求极限的方法 1) 单调有界准则; 2) 夹逼准则; 3) 极限运算准则及函数连续性; 4) 两个重要极限: a) 1sin lim 0=→x x x b) e x x x x x x =+=++∞→→)11(lim )1(lim 1 0 5) 无穷小代换:(0→x ) a) x x x x x arctan ~arcsin ~tan ~sin ~ b) 2 2 1~cos 1x x -
高等数学(同济第六版)上册期末复习重点
高等数学(同济第六版)上册期末复习重点 第一章:1、极限(夹逼准则) 2、连续(学会用定义证明一个函数连续,判断间断点类型) 第二章:1、导数(学会用定义证明一个函数是否可导)注:连续不一定可导,可导一定连续 2、求导法则(背) 3、求导公式也可以是微分公式 第三章:1、微分中值定理(一定要熟悉并灵活运用--第一节) 2、洛必达法则 3、泰勒公式拉格朗日中值定理 4、曲线凹凸性、极值(高中学过,不需要过多复习) 5、曲率公式曲率半径 第四章、第五章:积分 不定积分:1、两类换元法 2、分部积分法(注意加C ) 定积分: 1、定义 2、反常积分 第六章:定积分的应用 主要有几类:极坐标、求做功、求面积、求体积、求弧长 第七章:向量问题不会有很难 1、方向余弦 2、向量积 3、空间直线(两直线的夹角、线面夹角、求直线方程) 4、空间平面 5、空间旋转面(柱面)
第一章函数与极限 1、函数的有界性在定义域内有f(x)≥K1则函数f(x)在定义域上有下界,K1 为下界;如果有f(x)≤K2,则有上界,K2称为上界。函数f(x)在定义域内有界的充分必要条件是在定义域内既有上界又有下界。 2、数列的极限定理(极限的唯一性)数列{xn}不能同时收敛于两个不同的极限。 定理(收敛数列的有界性)如果数列{xn}收敛,那么数列{xn}一定有界。 如果数列{xn}无界,那么数列{xn}一定发散;但如果数列{xn}有界,却不能断定数列{xn}一定收敛,例如数列1,-1,1,-1,(-1)n+1…该数列有界但是发散,所以数列有界是数列收敛的必要条件而不是充分条件。 定理(收敛数列与其子数列的关系)如果数列{xn}收敛于a,那么它的任一子数列也收敛于a.如果数列{xn}有两个子数列收敛于不同的极限,那么数列{xn}是发散的,如数列1,-1,1,-1,(-1)n+1…中子数列{x2k-1}收敛于1,{xnk}收敛于-1,{xn}却是发散的;同时一个发散的数列的子数列也有可能是收敛的。 3、函数的极限函数极限的定义中0<|x-x0|表示x≠x0,所以x→x0时f(x)有没有极限与f(x)在点x0有没有定义无关。 定理(极限的局部保号性)如果lim(x→x0)时f(x)=A,而且A>0(或A<0),就存在着点那么x0的某一去心邻域,当x在该邻域内时就有f(x)>0(或f(x)>0),反之也成立。 函数f(x)当x→x0时极限存在的充分必要条件是左极限右极限各自存在并且相等,即f(x0-0)=f(x0+0),若不相等则limf(x)不存在。 一般的说,如果lim(x→∞)f(x)=c,则直线y=c是函数y=f(x)的图形水平渐近线。如果lim(x→x0)f(x)=∞,则直线x=x0是函数y=f(x)图形的铅直渐近线。 4、极限运算法则定理有限个无穷小之和也是无穷小;有界函数与无穷小的乘积是无穷小;常数与无穷小的乘积是无穷小;有限个无穷小的乘积也是无穷小;定理如果F1(x)≥F2(x),而limF1(x)=a,limF2(x)=b,那么a≥b. 5、极限存在准则两个重要极限lim(x→0)(sinx/x)=1;lim(x→∞)(1+1/x)x=1.夹逼准则如果数列{xn}、{yn}、{zn}满足下列条件:yn≤xn≤zn且limyn=a,limzn=a,那么limxn=a,对于函数该准则也成立。 单调有界数列必有极限。 6、函数的连续性设函数y=f(x)在点x0的某一邻域内有定义,如果函数f(x)当x→x0时的极限存在,且等于它在点x0处的函数值f(x0),即lim(x→x0)f(x)=f(x0),那么就称函数f(x)在点x0处连续。 不连续情形:1、在点x=x0没有定义;2、虽在x=x0有定义但lim(x→x0)f(x)不存在;3、虽在x=x0有定义且lim(x→x0)f(x)存在,但lim(x→x0)f(x)≠f(x0)时则称函数在x0处不连续或间断。 如果x0是函数f(x)的间断点,但左极限及右极限都存在,则称x0为函数f(x)的第一类间断点(左右极限相等者称可去间断点,不相等者称为跳跃间断点)。非第一类间断点的任何间断点都称为第二类间断点(无穷间断点和震荡间断点)。 定理有限个在某点连续的函数的和、积、商(分母不为0)是个在该点连续的函数。 定理如果函数f(x)在区间Ix上单调增加或减少且连续,那么它的反函数x=f(y)在对应的区间
同济大学2016-2017学年高等数学(B)上期末考试试卷
本资料仅供参考复习练手之用,无论是重修只求及格,还是为了拿优保研,复习课本上的基础知识点和例题、课后习题才是重中之重,作为一个重修过高数的学长,望大家不要舍本求末,记住这样一句话,只有当你付出了,你才可能有收获。 同济大学2016-2017学年第一学期高等数学B(上)期终试卷 一. 选择填空题(3'824'?=) 1. ()y f x =具有二阶导数, 且'()0f x ≠. 若曲线()y f x =在00(,)x y 的曲率为0k ≠, 其 反函数1()x f y -=所表示的曲线在对应点的曲率为'k , 则有 【A 】 ()'A k k = ; 1 ()'B k k =; ()C 'k k >; ()'D k k <. 2. 已知函数()y f x =满足(0)1f =, 如果在任意点x 处, 当x ?充分小时都有 2 ()1x y x o x x ?= ?+?+, 则有 【C 】 2 22 1()()(1)x A f x x -=+; 2()()11x B f x x =++; () C ()l 1 f x =+; ()D 题中所给的条件无法得到确定的函数()f x . 3. 下面的极限式中哪项等于连续函数()f x 的定积分 2 ()f x dx ? . 【D 】 12()l i m ()n n k k A f n n →∞=∑; 121()lim ()n n k k B f n n →∞=∑; 11()lim ()n n k k C f n n →∞=∑; 1 1 ()lim 2()n n k k D f n n →∞=∑. 4. 要使反常积分 +∞ ? 收敛, 则实数p 的取值范围是 【C 】 ()1A p >; ()1B p <; ()2C p >; ()2D p <. 5. 如果作换元sin x t =, 则积分3 (sin )f x dx π = ? .
高等数学同济第七版上册课后答案
习题1-10 1.证明方程x5-3x=1至少有一个根介于1和2之间. 证明设f(x)=x5-3x-1,则f(x)是闭区间[1, 2]上的连续函数. 因为f(1)=-3,f(2)=25,f(1)f(2)<0,所以由零点定理,在(1, 2)内至少有一点ξ(1<ξ<2),使f(ξ)=0,即x=ξ是方程x5-3x=1的介于1和2之间的根. 因此方程x5-3x=1至少有一个根介于1和2之间. 2.证明方程x=a sin x+b,其中a>0,b>0,至少有一个正根,并且它不超过a+b. 证明设f(x)=a sin x+b-x,则f(x)是[0,a+b]上的连续函数. f(0)=b,f(a+b)=a sin (a+b)+b-(a+b)=a[sin(a+b)-1]≤0. 若f(a+b)=0,则说明x=a+b就是方程x=a sin x+b的一个不超过a+b的根; 若f(a+b)<0,则f(0)f(a+b)<0,由零点定理,至少存在一点ξ∈(0,a+b),使f(ξ)=0,这说明x=ξ也是方程x=a sin x+b的一个不超过a+b的根. 总之,方程x=a sin x+b至少有一个正根,并且它不超过a+b. 3.设函数f(x)对于闭区间[a,b]上的任意两点x、y,恒有 |f(x)-f(y)|≤L|x-y|,其中L为正常数,且f(a)?f(b)<0.证明:至少有一点ξ∈(a,b),使得f(ξ)=0. .
. 证明 设x 0为(a , b )内任意一点. 因为 0||lim |)()(|lim 0000 0=-≤-≤→→x x L x f x f x x x x , 所以 0|)()(|lim 00 =-→x f x f x x , 即 )()(lim 00 x f x f x x =→. 因此f (x )在(a , b )内连续. 同理可证f (x )在点a 处左连续, 在点b 处右连续, 所以f (x )在[a , b ]上连续. 因为f (x )在[a , b ]上连续, 且f (a )?f (b )<0, 由零点定理, 至少有一点ξ∈(a , b ), 使得f (ξ)=0. 4. 若f (x )在[a , b ]上连续, a 高等数学 (同济第七版 )上册 -知识点总结 第一章 函数与极限 一. 函数的概念 1. 两个无穷小的比较 设 lim f (x) 0,lim g(x) 0且 lim 1) l = 0 ,称f (x) 是比g(x) 高 阶的无穷小,记以 f (x) = 0[ g(x) ] ,称g(x) 是比 f(x) 低阶的无穷小。 (2)l ≠ 0,称f (x) 与g(x) 是同阶无穷小。 (3)l = 1 ,称f (x) 与g(x) 是等价无穷小,记以 f (x) ~ g(x) 2. 常见的等价无穷小 当 x →0时 sin x ~ x , tan x ~ x , arcsin x ~ x , arccosx ~ x , 1- cos x ~ x^2/2 , e x -1 ~ x ,ln(1 x) ~ x ,(1 x) 1~ x 求极限的方法 1.两个准则 准则 1. 单调有界数列极限一定存在 准则 2. (夹逼定理)设 g(x) ≤ f (x) ≤ h(x) 若 lim g(x) A,lim h(x) A ,则 lim f (x) A 2.两个重要公式 3.用无穷小重要性质和等价无穷小代换 4.用泰勒公式 当 x 0 时,有以下公式,可当做等价无穷小更深层次 23 e x 1 x x x 2! 3! 35 xx sinx x ... ( 1) 3! 5! (2n 1)! g f ((x x )) l 公式 1 sin x 公式 2 l im(1 x) n x n! o(x n ) 2n 1 n x 2n 1 n o(x 2n 1) 2 4 2n x x n x 2n cosx 1 ... ( 1)n o(x 2n ) 2! 4! 2n! 2 3 n ln(1 x) x x x ... ( 1)n 1 x o(x n ) 2 3 n ( 1) 2 ( 1)...( (n 1)) n n (1 x) 1 x x 2 ... x n o(x n ) 2! n! 3 5 2n 1 x x n 1 x 2n 1 arctan x x ... ( 1) o(x ) 3 5 2n 1 5.洛必达法则 定理 1 设函数 f (x) 、 F ( x)满足下列条件: (1) lim f(x) 0, lim F(x) 0; x x 0 x x 0 (2) f(x)与 F(x)在 x 0的某一去心邻域内可导,且 F (x) 0; (3) lim f (x) 存在(或为无穷大) ,则lim f(x) lim f (x) x x 0 F (x) x x 0 F(x) x x 0 F (x) 这个定理说明:当 lim f (x) 存在时, lim f (x) 也存在且等于 lim f (x) ;当 x x0 F (x) x x0 F(x) x x0 F (x) lim f (x) 为无穷大时, lim f(x) 也是无穷大. x x 0 F (x) x x 0 F(x) 这种在一定条件下通过分子分母分别求导再求极限来确定未定式的极限值 的方法称为洛必达( LH ospital )法则 . 型未定式 定理 2 设函数 f (x) 、 F(x)满足下列条件: 注:上述关于 x x 0时未定式 型的洛必达法则,对于 x 时未定式 型 同样适用. 使用洛必达法则时必须注意以下几点: (1)洛必达法则只能适用于“ 0 ” 和“ ”型的未定式,其它的未定式须 0 先化简变形成“ 0 ”或“ ”型才能运用该法则; (2)只要条件具备,可以连续应用洛必达法则; (3) 洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不 能断定原极限不存在. 6.利用导数定义求极限 基本公式 li x m 0 f (x 0 x) f(x 0) f '( x 0 ) (如果存在) 7. 利用定积分定义求极限 基本格式 lim 1 f(k ) f (x)dx (如果存在) n n k 1 n 0 1) 2) 3) lim f(x) , lim F(x) ; x x 0 x x 0 f(x)与 F(x)在 x 0的某一去心邻域内可导,且 F (x) 0; F f ((x x )) 存在(或为无穷大),则 x lim x 0 f (x) F(x) lim f (x) x x 0 F (x) 高等数学第六版上册课后习题答案及解析 第一章 习题1-1 1. 设A =(- , -5) (5, + ), B =[-10, 3), 写出A B , A B , A \B 及A \(A \B )的表达式. 解 A B =(- , 3) (5, + ), A B =[-10, -5), A \ B =(- , -10) (5, + ), A \(A \B )=[-10, -5). 2. 设A 、B 是任意两个集合, 证明对偶律: (A B )C =A C B C . 证明 因为 x (A B )C x A B x A 或x B x A C 或x B C x A C B C , 所以 (A B )C =A C B C . 3. 设映射f : X Y , A X , B X . 证明 (1)f (A B )=f (A ) f (B ); (2)f (A B ) f (A ) f (B ). 证明 因为 y f (A B ) x A B , 使f (x )=y (因为x A 或x B ) y f (A )或y f (B ) y f (A ) f (B ), 所以 f (A B )=f (A ) f (B ). (2)因为 y f (A B ) x A B , 使f (x )=y (因为x A 且x B ) y f (A )且y f (B ) y f (A ) f (B ), 所以 f (A B ) f (A ) f (B ). 4. 设映射f : X Y , 若存在一个映射g : Y X , 使X I f g = , Y I g f = , 其中 I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x X , 有I X x =x ; 对于每一个y Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.高等数学(同济第七版)(上册)_知识点总结
高等数学第六版(同济大学)上册课后习题答案解析
