关于公布湖州市2008年高中数学竞赛高二A组获奖结果的通
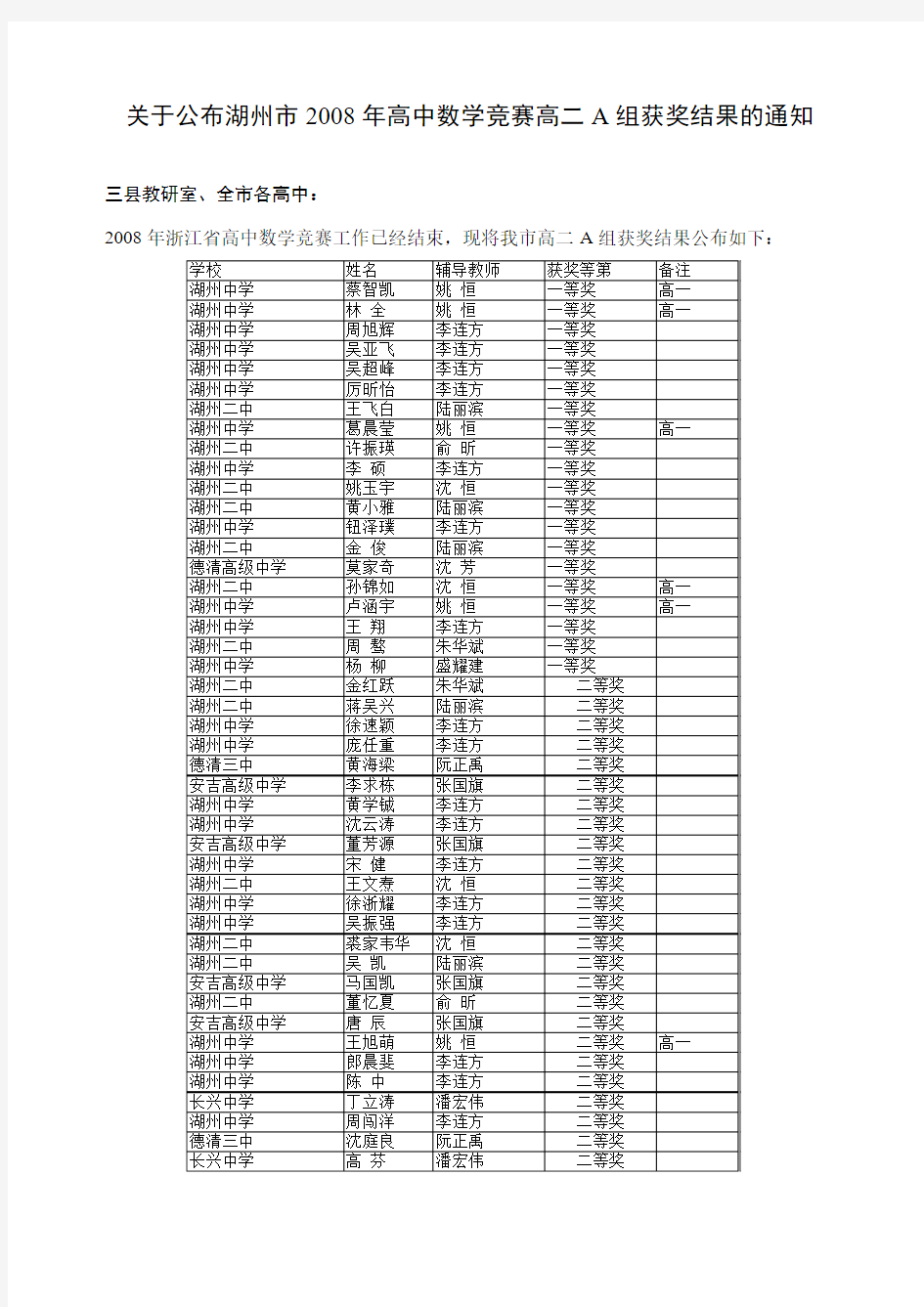

关于公布湖州市2008年高中数学竞赛高二A组获奖结果的通知
三县教研室、全市各高中:
2008年浙江省高中数学竞赛工作已经结束,现将我市高二A组获奖结果公布如下:
湖州市教育学会中学数学教学分会
2008年4月18日
人教版小学五年级上册数学竞赛试题
五年级数学知识竞赛试卷 班级———姓名————座号——评分———— 一、我会填。(23分,其中11至14题每空2分) 1、一个三位小数四舍五入到百分位是3.32,这个数最大是(),最小是()。 2、两个数相除的商是0.8,被除数扩大100倍,除数缩小10倍,商是()。 3、11÷7的商小数点后第50位是()。 4、在0.978、0.978、0.978、0.978四个数中最大的是(),最小是()。 5、一条彩带长6.4米,每1.6米剪一段,需要剪()次才能完成。 6、60升的油装入容量为6.5升的油桶中,需要()只这样的油桶才够装。 7、用一杯子向空瓶倒水,如果倒进3杯水,连瓶共重440克,如果倒进5杯水,连瓶共重600克,一杯水重()克,空瓶重()克。 8、把一个小数的小数点向右移动二位后,所得的数比原数增加了267.3,原数是()。 9、a去除一个数商7余5,这个数可表示为()。 10、在括号里填上﹥、﹤或= 。 0.95×2.34()2.34 0.98×0.87()0.87÷0.98 4.85×99+4.85()4.85×100 11、甲对乙说:“我的年龄是你的3倍,”,乙队甲说;“我5年后的年
龄和你去年的年龄一样”,乙今年()岁。 12、一个停车场停一次车至少要交0.5元的停车费,如果停车超时1小时,每多停0.5小时就要多交0.5元,这辆车一共交了5.5元,这辆车一共停了()小时。 13、小东奶奶今年的年龄减去15后,缩小4倍,再减去6之后,扩大10倍,恰好是100岁,小东的奶奶今年()岁。 14、右图中有()个三角形。 二、判断题。(5分) 1、小数点的后面添上0或去掉0,小数的大小不变。() 2、一个因数比1小时,积一定小于另一个因数。() 3、观察一个物体时,一次最多能看到3个面。() 4、无限小数一定大于有限小数。() 5、含有未知数的式子一定是方程。() 三、我会选(把正确答案的序号天灾括号里)。(5分) 1、如果a2=2a,那么a=()。 A、1 B、4 C、2 或 O D、无法确定 2、小刚今年(a-4)岁,小林今年a岁,再过x年后,他们相差()。 A、4岁 B、x岁 C、(a+4)岁 D、(x+4)岁 3、如果甲×1.1=乙÷1.1(甲、乙不为0),那么()。 A、甲=乙 B、甲﹥乙 C、甲﹤乙 D、无法确定 4、a÷b =c……7,若a 和 b 同时缩小10倍,则余数是()。 A、70 B、7 C、 0.7 D、0.07
高中数学竞赛模拟试题一汇总
高中数学竞赛模拟试题一 一 试 (考试时间:80分钟 满分100分) 一、填空题(共8小题,5678=?分) 1、已知,点(,)x y 在直线23x y += 上移动,当24x y +取最小值时,点(,)x y 与原点的距离是 。 2、设()f n 为正整数n (十进制)的各数位上的数字的平方之和,比如 ()22212312314 f =++=。记 1()() f n f n =, 1()(()) k k f n f f n +=, 1,2,3... k =,则 =)2010(2010f 。 3、如图,正方体1 111D C B A ABCD -中,二面角 1 1A BD A --的度数 是 。 4、在2010,,2,1 中随机选取三个数,能构成递增等差数列的概率是 。 5、若正数c b a ,,满足 b a c c a b c b a +- +=+,则c a b +的最大值是 。 6、在平面直角坐标系xoy 中,给定两点(1,2)M -和(1,4)N ,点P 在X 轴上移动,当MPN ∠取最大值时,点P 的横坐标是 。 7、已知数列...,,...,,,210n a a a a 满足关系式18)6)(3(1=+-+n n a a 且30=a ,则∑=n i i a 01 的值是 。 8、函数sin cos tan cot sin cos tan cot ()sin tan cos tan cos cot sin cot x x x x x x x x f x x x x x x x x x ++++=+++++++在(,)2 x o π∈时的最 小值为 。
二、解答题(共3题,分44151514=++) 9、设数列}{n a 满足条件:2,121==a a ,且 ,3,2,1(12=+=++n a a a n n n ) 求证:对于任何正整数n ,都有:n n n n a a 111+≥+ 10、已知曲线m y x M =-22:,0>x ,m 为正常数.直线l 与曲线M 的实轴不垂直,且依次交直线x y =、曲线M 、直线x y -=于A 、B 、C 、D 4个点,O 为坐标原点。 (1)若||||||CD BC AB ==,求证:AOD ?的面积为定值; (2)若BOC ?的面积等于AOD ?面积的3 1,求证:||||||CD BC AB == 11、已知α、β是方程24410()x tx t R --=∈的两个不等实根,函数=)(x f 1 22 +-x t x 的定义域为[,]αβ. (Ⅰ)求);(min )(max )(x f x f t g -= (Ⅱ)证明:对于) 2 ,0(π∈i u )3,2,1(=i ,若1sin sin sin 321=++u u u ,则 64 3 )(tan 1)(tan 1)(tan 1321<++u g u g u g . 二 试 (考试时间:150分钟 总分:200分) 一、(本题50分)如图, 1O 和2 O 与 ABC ?的三边所在的三条直线都相 切,,,,E F G H 为切点,并且EG 、FH 的 延长线交于P 点。 求证:直线PA 与BC 垂直。 二、(本题50分)正实数z y x ,,,满 足 1≥xyz 。证明: E F A B C G H P O 1。 。 O 2
2016年大梦杯福建初中数学竞赛试题参考答案
2016年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2016年3月13日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.在平面直角坐标系xOy 中,已知点(02)B ,,点A 在x 轴正半轴上且30BAO ∠=?。将 OAB △沿直线AB 折叠得CAB △,则点C 的坐标为( ) A .(13), B .(33), C .(33), D .(31), 【答案】 B 【解答】如图,设CD x ⊥轴于点D 。 依题意,23CA OA ==,260CAO BAO ∠=∠=?。 所以,3CD =,3AD =,3OD =。 因此,点C 的坐标为(33), 。 2.若实数a ,b 满足232a a +=,232b b +=,且a b ≠,则22(1)(1)a b ++=( ) A .18 B .12 C .9 D .6 【答案】 A 【解答】依题意,a ,b 为方程2320x x +-=的两个不同实根。 因此,由韦达定理得,3a b +=-,2ab =-。 []22(1)(1)(123)(123)9(1)(1)91()9(132)18a b a b a b a b ab ++=+-+-=--=-++=+-=。 或解:222222222(1)(1)11()2194418a b a b a b a b ab a b ++=+++=++-+=+++=。 3.若关于x 的方程22240224 x x x a x x x +-+++=-+-只有一个实数根,则符合条件的所有实数a 的值的总和为( ) A .6- B .30- C .32- D .38- 【答案】 D 【解答】方程 22240224 x x x a x x x +-+++=-+-化为22480x x a +++= ……………… ① 若方程①有两个相等实根,则168(8)0a =-+=△,6a =-。 6a =-时,方程①的根121x x ==-,符合要求。 若2x =是方程①的根,则8880a +++=,24a =-,此时,方程①的另一个根为4x =-,符合要求。 若2x =-是方程①的根,则8880a -++=,8a =-,此时,方程①的另一个根为0x =,符合要求。
六年级数学竞赛试题及答案
六年级数学竞赛试题 学校: 班级: 姓名: ★亲爱的同学,经过这段时间的中学数学学习,你的数学能力一定有了较大的提高,展示你才能的机会来了!祝你在这次数学竞赛中取得好成绩!别忘了要沉着冷静、细心答题哟! 一、选择题(每小题6分,共36分) 1、如果m 是大于1的偶数,那么m 一定小于它的……………………( ) A 、相反数 B 、倒数 C 、绝对值 D 、平方 2、当x=-2时, 37ax bx +-的值为9,则当x=2时,3 7ax bx +-的值是 ( ) A 、-23 B 、-17 C 、23 D 、17 3、255 ,344 ,533 ,622 这四个数中最小的数是………………………( ) A. 255 B. 344 C. 533 D. 622 4、把14个棱长为1的正方体,在地面上堆叠成如图1所示的立体,然后将露出的表面部分染成红色.那么红色部分的面积为 ( ). A 、21 B 、24 C 、33 D 、37 5、有理数的大小关系如图2所示,则下列式子 中一定成立的是…… ( ) A 、c b a ++>0 B 、c b a <+ C 、c a c a +=- D 、a c c b ->-
6、某动物园有老虎和狮子,老虎的数量是狮子的2倍。每只老虎每天吃肉4.5千克,每只狮子每天吃肉3.5千克,那么该动物园的虎、狮平均每天吃肉…… …… ( ) A 、 625千克 B 、 725千克 C 、825千克 D 、9 25千克 二、填空题(每小题6分,共36分) 7、定义a*b=ab+a+b,若3*x=27,则x 的值是_____ 8、三个有理数a、b、c之积是负数,其和是正数,当x = c c b b a a + + 时,则 ______29219=+-x x 。 9、当整数m =_________ 时,代数式 1 36 -m 的值是整数。 10、A 、B 、C 、D 、E 、F 六足球队进行单循环比赛,当比赛到某一天时,统计出A 、B 、C 、D 、E 、五队已分别比赛了5、4、3、2、1场球,则还没与B 队比赛的球队是______ 。 11、甲从A 地到B 地,去时步行,返回时坐车,共用x 小时,若他往返都座车,则全程 只需x 3 小时,,若他往返都步行,则需____________小时。 12、 ._______2007 20061431321211=?+?+?+?K 三、解答题(共28分) 13、现将连续自然数1至2009按图中的方式排列成一个长方形队列,再用正方形任意框出16个数。(14分) (1)设任意一个这样的正方形框中的最小数为n ,请用n 的代数式表示该框中的16个数,然后填入右表中相应的空格处,并求出这16个数中的最小数和最大数,然后填入右表中相应的空格处,并求出这16个数的和。(用n 的代数式表示) (2)在图中,要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能?若不可能,请说明理由;若可能,请求出该正方形框出的16个数中的最小数和最大数。 图1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 · · · · · · · 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 图2
三年级上数学竞赛试卷
2016-2017年三年级数学竞赛试题 一、你知道吗填一填。(每空2分,共32分) 1、350×4的积的末尾有()个0,积是()。 2、一个长方形的草坪周长是240米,长是70米,宽是()米,合()厘米。 3、用4个边长是3厘米的小正方形拼成一个大正方形,这个大正方形的周长是()厘米。 4、在〇里填上“>”、“<”或“=”。 3分○300秒 48毫米○50厘米 2米○200厘米 400千克○1吨 5、一根4分米长的绳子,对折再对折后,每段绳子长()厘米。 6、林叔今年34岁,林芳今年8岁,12年后,林叔和林芳相差()岁。 7、在“A÷9=B……C”中,其中B、C都是一位数,A最大是()。 8、菜场运来白菜和萝卜共75筐,白菜是萝卜的2倍,运来白菜()筐,白菜()筐。 9、一个两位数,其数字和是7,如果此数减去27,则两个数的位置正好互换。原来的两位数是()。 10、一根木料锯成3段要6分钟。如果每次锯的时间相同,那么锯7段要()分钟。 二、公正小法官(对的打∨,错的打×) (5分) 1、7×7和7+7意义相同。() 2、5千克的纸和5千克的铁球一样重。() 3、一个正方形的边长增加2厘米,它的周长增加8厘米。() 4、如果A×B=0,那么A和B中至少有一个是0。() 5、一个三位数和9相乘,积一定是四位数。() 三、我真棒能计算。(28分) 1、口算。(12分) 65–45 = 30×10= 3000×5= 500-60= 120×30= 505÷5= 960÷3= 0÷30= 51×9= 18÷5= 90×(50-50)= 350÷5= 2、列竖式计算。(4+3+3=10分) 409+391= 64÷9= 900-461= 验 算: 3、脱式计算。(6分) 483×2-751 205×9 +452 183×(36÷9)
2018全国高中数学联赛试题
2018年全国高中数学联合竞赛一试试题(A 卷) 一、填空题:本大题共 8小题,每小题 8分,共64分. 1.设集合{1,2,3,,99}A = ,{2}B x x A =∈,{2}B x x A =∈,则B C 的元素个数 . 解析:因为{1,2,3,,99}A = ,所以{2,4,6,,198}B = ,{1,2,3,,49}C = ,于是 {2,4,6,,48}B C = ,共24个元素. 2.设点P 到平面α Q 在平面α上,使得直线PQ 与α所成角不小于30 且不大于60 ,则这样的点Q 所构成的区域的面积为 . 解析:过点P 作平面α的垂线,这垂足为O ,则点Q 的轨迹是以O 为圆心,分别以1ON =和3OM =为半径的扇环,于是点Q 所构成的区域的面积为21S S S =-= 9 8πππ-=. 3. 将1,2,3,4,5,6随机排成一行,记为,,,,,a b c d e f ,则abc def +是偶数的概率为 . 解析:(直接法)将1,2,3,4,5,6随机排成一行,共有6 6720A =种不同的排法,要使 abc def +为偶数,abc 为与def 同为偶数或abc 与且def 同为奇数. (1)若,,a b c 中一个偶数两个奇数且,,d e f 中一个奇数两个偶数. 共324种情形; (2)若,,a b c 中一个奇数两个偶数且,,d e f 中一个偶数两个奇数. 共324种情形; 共有648种情形.综上所述,abc def +是偶数的概率为 6489 72010 =. (间接法)“abc def +是偶数”的对立事件为“abc def +是偶数”, abc def +是偶数分成两种情况:“abc 是偶数且def 是奇数”或“abc 是奇数且def 是偶数”,每 P O M N α
大梦杯福建省初中数学竞赛试题参考答案及评分标准
大梦杯福建省初中数学竞赛试题参考答案及评分标 准 The latest revision on November 22, 2020
2018年“大梦杯”福建省初中数学竞赛试题 考试时间 2018年3月18日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( ) A .3- B .2- C .1- D .1 2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。坐标原点O 为 AD 的中点,A 、D 、E 在y 轴上。若二次函数2y ax =的图像过C 、F 两点,则n m =( ) A .31+ B .21+ C .231- D .221- 3.如图,G 为ABC △的重心,点D 在CB 延长线上,且1 2 BD BC =,过D 、G 的直线交AC 于点E ,则 AE AC =( ) A .2 5 B .3 5 C . 3 7 D . 47 4.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=?,若ABC △外接圆的半径 为2,则AH =( ) A .23 B .22 C .4 D .31+ 5.满足方程22419151x xy y -+=的整数对()x y , 有( ) H O B C A (第4题图) (第2题图) E G B D (第3题图)
三年级上册数学竞赛试题
班级____________姓名______________成绩__________ 一、填空。(共31分,每小题4分,其中第4小题8分,第6小题7分。) 1、360秒=()分1千米-520米=()米 2千克68克=()克2时35分=()分 2、北京奥运会一场足球赛从下午3:30分开始,经过1小时55分后结束,这场足球赛结束的时间是()时()分。 3、将下列数量按从大到小的顺序排列:5600分米,5000厘米,550米,1千米60米 4、在算式□÷△=3……○中,当余数是4时,除数最小是(),被除数就是()。当除数是6时,余数最大是(),被除数最小是()。 5、一串彩灯有四种颜色,并且是按第一盏红、第二盏蓝、第三盏黄、第四盏绿这样的顺序排列的,照这样下去,第12盏是()色,第39盏是()色。 6、在小明的日记里填上合适的单位。 我家门前有一棵高5()的大树,家里有一台长约8()的电视、一张长约3()的沙发,阳台有一台90()高的洗衣机,书房里有一张6()高的书桌,书桌上有一盏高35()的台灯和一个厚约30()的文具盒。 二、选择题。(9分) 1、一幅画长12分米,宽8分米。这幅画放在下面第()个画架中最合适。 A、长14分米宽6分米 B、长16分米宽12分米 C、长13分米宽9分米 2、如右图,剪下一小长方形后,周长()。 A、变大了 B、变小了 C、不变 3、一筐苹果有50个,最少要增加()个,才能平均分给7个小朋友而刚好够分。最少拿走()个,就能刚好平均分给8个小朋友。 A、2 B、6 C、无法确定 三、作图题(10分)(1)画一条线将下边的图形改为平行四边形。(4分)(2)在图形的左边画一个与这个平行四边形对称的图形。(6分)
历年全国高中数学联赛试题及答案
1988年全国高中数学联赛试题 第一试(10月16日上午8∶00——9∶30) 一.选择题(本大题共5小题,每小题有一个正确答案,选对得7分,选错、不选或多选均得0分): 1.设有三个函数,第一个是y=φ(x ),它的反函数是第二个函数,而第三个函数的图象及第二个函数的图象关于x +y=0对称,那么,第三个函数是( ) A .y=-φ(x ) B .y=-φ(-x ) C .y=-φ-1(x ) D .y=-φ- 1(-x ) 2.已知原点在椭圆k 2x 2+y 2-4kx +2ky +k 2-1=0的内部,那么参数k 的取值范围是( ) A .|k |>1 B .|k |≠1 C .-1
2018年“大梦杯”福建省初中数学竞赛试题参考答案
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准 一、选择题(共5小题,每小题7分,共35分) 01.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32 442m m m ++-的值为( A ) A .3- B .2- C .1- D .1 【解答】依题意,2 1616(31)0m m D =++=,∴2 310 m m ++=,∴231m m =--,2 31m m +=-。 ∴3 2 2 2 442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。 02.如图,正方形ABCD 和正方形DEFG 的边长分别为()m n m n <、 。原点O 为AD 的中点,A D E 、、在y 轴上。若二次函数2 y ax =的图像经过C F 、 两点,则n m =( B ) A 1 B 1 C .1 D .1 【解答】依题意,点C 的坐标为()2m m ,,点F 的坐标为()2 m n n -+,。 由二次函数2 y ax =的图像经过C F 、两点得22 2()2 m am m n a n ì=??í?+=-??, 消去a 得22 20n mn m --=。 ∴2210n n m m 骣-?=琪桫 ,解得1n m =(舍负根)。∴ n m =03.如图,G 为ABC △的重心,点D 在CB 延长线上且12BD BC =,直线 A .25 B .35 C .37 D .4 7 ( D ) F B D F B 【解答】如图,连AG ,并延长交BC 于点F 。 ∵G 为ABC △的重心且12BD BC = ,∴F 为BC 中点且21 AG GF =,DB BF FC ==。 过点F 作FM DE ∥,交AC 于点M ,则13CM CF CE CD ==,2 1 AE AG EM GF ==。 设CM k =,则3CE k =,2EM k =,4AE k =,∴7AC k =,44 77AE k AC k ==。 另解:如图,连AG ,并延长交BC 于点F 。∵G 为ABC △的重心且1 2 BD BC =, ∴F 为BC 中点且21AG GF =,DB BF FC ==,∴23FD DC =,2 1 AG GF =。 在AFC △中,由梅涅劳斯定理得1FD CE AG DC EA GF 鬃=,22131CE EA 鬃=,34CE EA =,∴4 7 AE AC =。 (第03题答题图2) (第03题答题图1) (第03题图)
高中数学竞赛试卷A及答案
高中数学竞赛试卷A 及答案 考生注意:1、本试卷共三大题(16个小题),全卷满分150分。 2、用钢笔、签字笔或圆珠笔作答。 3、解题书写不要超出装订线。 4、不能使用计算器。 一、选择题(本大题共6小题,每小题6分,满分36分。在每小题给出的四个选项中,只有一项是符合题目要求的。) 1.记[x]为不大于x 的最大整数,设有集合}2]x [x |x {A 2=-=,}2|x ||x {B <=,则=B A ( ) A .(-2,2) B .[-2,2] C .}1,3{- D .}1,3{- 2.若()() 2006 34554 x 57x 53x 2x 2x f +--+=,则??? ? ??-21111f = ( ) A .-1 B . 1 C . 2005 D .2007 3.四边形的各顶点位于一个边长为1的正方形各边上,若四条边长的平方和为t ,则t 的取值区间是 ( ) A .[1,2] B .[2,4] C .[1,3] D .[3,6] 4.如图,在正方体ABCD -A 1B 1C 1D 1中,P 为棱 AB 上一点,过点P 在空间作直线l ,使l 与平面 ABCD 和平面ABC 1D 1均成 30角,则这样的直 线条数是 ( ) A . 1 B . 2 C . 3 D . 4 5.等腰直角三角形?ABC 中,斜边BC=24,一个 椭圆以C 为其焦点,另一个焦点在线段AB 上,且 椭圆经过A ,B 两点,则该椭圆的标准方程是(焦点在x 轴上) ( ) A .12 4y 246x 22=+ + B . 12 43y 2 46x 22=++ + C . 1246y 24x 2 2 =++ D . 1246y 243x 2 2 =++ + (注:原卷中答案A 、D 是一样的,这里做了改动) 6.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个数为 ( ) A .1372 B . 2024 C . 3136 D .4495 二、填空题(本大题共6小题,每小题6分,满分36分,请将正确答案填在横线上。) A C D
级上数学竞赛试卷
二年级数学竞赛试题 得分: 一、填空题。(38分) 1、最大的一位数与最小的两位数相加的和是( )。 2、请你根据口诀“三四一十二”,在下面的括号里写出两个乘法算式: ( ) ,( )。 3、 (1)上面共有( )个 。 (2)根据上图写成加法算式是( ),写成乘法算 式是( )。 4、在 里填上“+、-、×、>、<或=”。 3○5=15 3×4〇4×5 26+20○45 40○4=36 2×2○2+2 2×5+5○5×3-5 5、在括号里填上合适的数。 5 10 □ □ □ 30 □ · · · · · · · · · · · · · · □ 16 14 □ □ 8 □ 6、数一数。 有( )个☆,四种图形总共有( )个。 7、小丽在图画本上画了 ☆☆☆ 和一些 ○ 和 △,其中 ○ 的个数比 ☆ 多5个, ○ 有( )个,△ 的个数是 ☆ 和 ○ 的总数,△ 有( )个。 8、已知 □+△=25,△+△=16,请你算一算:□=( ) △=( )。 二、我是小法官。〔对的打“√”,错的打“×”〕(3分) 1、因为2×2=2+2,所以3×3=3+3。 ( ) 2、5张2元人民币和2张5元人民币的钱数一样多。 ( ) 3、5+5+5+5=20可以写成乘法算式是4×5=20或5×4=20。 ( ) 三、看图列算式。(11分) 1、 加法算式: 乘法算式: 读作:( )乘( ) 2、 加法算式: 乘法算式: 读作:( )乘( ) 3、把 与对应的连起来。 …………………密……………封……………线……………内……………不……………要…………… ……密……………封……………线……………内……………不……………要……………答……………密……………封……………线……………内……………不……………要……………答…………… 班级_ 姓名 座号 5×2 5×4 3×4 4×4 3×3 9 20 16 12 10
2015年全国高中数学联赛试题
2015年全国高中数学联合竞赛一试试题(A 卷) 一、填空题:本大题共8小题,每小题8分,满分64分 1.设,a b 为不相等的实数,若二次函数2()f x x ax b =++满足()()f a f b =,则(2)f 的值为 2.若实数α满足cos tan αα=,则41cos sin αα +的值为 3.已知复数数列{}n z 满足111,1(1,2,3,)n n z z z ni n +==++=,其中i 为虚数单位,n z 表示n z 的共轭复数,则2015z 的值为 4.在矩形ABCD 中,2,1AB AD ==,边DC (包含点,D C )上的动点P 与CB 延长线上(包含点B )的动点Q 满足DP BQ =,则向量PA 与向量PQ 的数量积PA PQ ?的最小值为 5.在正方体中随机取3条棱,它们两两异面的概率为 6.在平面直角坐标系xOy 中,点集{}(,)(36)(36)0K x y x y x y =+-+-≤所对应的平面区域的面积为 7.设ω为正实数,若存在,(2)a b a b ππ≤<≤,使得sin sin 2a b ωω+=,则ω的取值范围是 8.对四位数(19,0,,9)abcd a b c d ≤≤≤≤,若,,a b b c c d ><>,则称abcd 为P 类数,若 ,,a b b c c d <><,则称abcd 为Q 类数,用(),()N P N Q 分别表示P 类数与Q 类数的个数,则 ()()N P N Q -的值为 二、解答题:本大题共3小题,满分56分,解答应写出文字说明、证明过程或演算步骤 9.(本题满分16分)若实数,,a b c 满足242,424a b c a b c +=+=,求c 的最小值. 10.(本题满分20分)设1234,,,a a a a 是4个有理数,使得 {}311424,2,,,1,328i j a a i j ??≤<≤=----???? ,求1234a a a a +++的值. 11.(本题满分20分)在平面直角坐标系xOy 中,12,F F 分别是椭圆2 212 x y +=的左、右焦点,设不经过焦点1F 的直线l 与椭圆交于两个不同的点,A B ,焦点2F 到直线l 的距离为d ,如果直线11,,AF l BF 的斜率依次成等差数列,求d 的取值范围.
-2017年大梦杯福建省初中数学竞赛试题
2017年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2017年3月19日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.设a =1 a a + 的整数部分为( ) A .1 B .2 C .3 D .4 【答案】 B 【解答】由2226a =+-=,知a = 于是1 a a + =2111()62866a a +=++=+,214()9a a <+<。 因此,1 a a + 的整数部分为2。 (注: a ==== 2.方程2 2( )32 x x x +=-的所有实数根之和为( ) A .1 B .3 C .5 D .7 【答案】 A 【解答】方程2 2( )32 x x x +=-化为2222(2)3(2)x x x x -+=-。 即3251060x x x -+-=,2(1)(46)0x x x --+=。 解得1x =。经检验1x =是原方程的根。 ∴ 原方程所有实数根之和为1。 3.如图,A 、B 、C 三点均在二次函数2y x =的图像上,M 为线段AC 的中点,BM y ∥轴,且2MB =。设A 、C 两点的横坐标分别为1t 、2t (21t t >),则21t t -的值为( ) A .3 B . C .± D .【答案】 D 【解答】依题意线段AC 的中点M 的坐标为22 1212 ()22 t t t t ++,。 (第3题)
由BM y ∥轴,且2BM =,知B 点坐标为22 1212 (2)22t t t t ++-,。 由点B 在抛物线2 y x =上,知22 212122()22 t t t t ++-=。 整理,得2222 121122 2282t t t t t t +-=++,即221()8t t -=。 结合21t t > ,得21t t -= 4.如图,在Rt ABC △中,90ABC ∠=?,D 为线段BC 的中点,E 在线段AB 内,CE 与AD 交于点F 。若A E E F =,且7AC =,3FC =,则c o s A C B ∠的值为( ) A .37 B . C .314 D 【答案】 B 【解答】如图,过B 作BK AD ∥与CE 的延长线交于点K 。 则由AE EF =可得,EBK EAF AFE BKE ∠=∠=∠=∠。 ∴ EK EB =。 又由D 为BC 中点,得F 为KC 中点。 ∴ 3AB AE EB FE EK KF FC =+=+===。 ∴ BC === ∴ cos 7 BC ACB AC ∠= = 。 或解:对直线AFD 及BCE △应用梅涅劳斯定理得, 1BD CF EA DC FE AB ??=。 由D 为线段BC 的中点,知BD DC =。 又AE EF =,因此,3AB CF ==。 结合7AC =,90ABC ∠=? ,利用勾股定理得,BC = 所以,cos 7 BC ACB AC ∠==。 D B A E (第4题) K
全国大学生数学竞赛试题及答案
河北省大学生数学竞赛试题及答案 一、(本题满分10 分) 求极限))1(21(1 lim 222222--++-+-∞→n n n n n n Λ。 【解】 ))1(21(12 22222--++-+-= n n n n n S n Λ 因 21x -在]1,0[上连续,故dx x ?1 02-1存在,且 dx x ? 1 2 -1=∑-=∞→-1 21 .)(1lim n i n n n i , 所以,= ∞ →n n S lim n dx x n 1lim -11 2∞→-? 4 -1102π ==?dx x 。 二、(本题满分10 分) 请问c b a ,,为何值时下式成立.1sin 1 lim 22 0c t dt t ax x x b x =+-?→ 【解】注意到左边得极限中,无论a 为何值总有分母趋于零,因此要想极限存在,分子必 须为无穷小量,于是可知必有0=b ,当0=b 时使用洛必达法则得到 22 022 01)(cos lim 1sin 1lim x a x x t dt t ax x x x x +-=+-→→?, 由上式可知:当0→x 时,若1≠a ,则此极限存在,且其值为0;若1=a ,则 21)1(cos lim 1sin 1lim 22 220-=+-=+-→→?x x x t dt t ax x x x b x , 综上所述,得到如下结论:;0,0,1==≠c b a 或2,0,1-===c b a 。 三、(本题满分10 分) 计算定积分? += 2 2010tan 1π x dx I 。
【解】 作变换t x -= 2 π ,则 =I 22 20π π = ?dt , 所以,4 π= I 。 四、(本题满分10 分) 求数列}{1n n - 中的最小项。 【解】 因为所给数列是函数x x y 1- =当x 分别取ΛΛ,,,3,2,1n 时的数列。 又)1(ln 21-=--x x y x 且令e x y =?='0, 容易看出:当e x <<0时,0<'y ;当e x >时,0>'y 。 所以,x x y 1-=有唯一极小值e e e y 1)(-=。 而3 3 1 2 132> ? < 七年级(上)数学竞赛试题 班级 姓名 得分: 一、填空题(每小题3分,共30分) 1、有理数在数轴上的位置如图1所示,化简 2、已知:5||=a ,且0=+b a ,则_______=-b a ; 3、若0232=--a a ,则______6252 =-+a a 4、 已知x=5时,代数式ax 3+ bx -5的值是10,当x=-5时,代数式ax 3+bx+5= 。 5.(-2124 +7113 ÷24113 -38 )÷1512 = 。 6. 已知 与是同类项,则=__。 7、.有一列数,按照下列规律排列:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6,7,……这列数的第200个数是__________. 8、._______2019 20181431321211=?+?+?+? 9、某班学生去参加义务劳动,其中一组到一果园去摘梨子,第一个进园的学生摘了1个梨子,第二个学生摘了2个,第三个学生摘了3个,……以此类推,后来的学生都比前面的学生多摘1个梨子,这样恰好平均每个学生摘了6个梨子,请问这组学生的人数为 人。 10、某班45人参加一次数学比赛,结果有35人答对了第一题,有27人答对了第二题,有41人答对了第三题,有38人答对了第四题,则这个班四道题都对的同学至少有 人. 二、选择题(每小题3分,共24分) 11、(-0.125)2018×(-8)2019的值为( ) (A )-4 (B )4 (C)-8 (D)8 12、若,,,a b c m 是有理数,且23,2a b c m a b c m ++=++=,那么b 与c ( ) (A )互为相反数 (B )互为倒数 (C )互为负倒数 (D )相等 13.有理数a 等于它的倒数,则a 2016是( ) 1 2016年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2016年3月13日 9∶00-11∶00 满分150分 一、选择题(共5小题,每小题7分,共35分)。每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.在平面直角坐标系xOy 中,已知点(02)B ,,点A 在x 轴正半轴上且30BAO ∠=?。将 OAB △沿直线AB 折叠得CAB △,则点C 的坐标为( ) A .(1 B .3) C .(3 D .1) 2.若实数a ,b 满足232a a +=,232b b +=,且a b ≠,则22(1)(1)a b ++=( ) A .18 B .12 C .9 D .6 3.若关于x 的方程22240224 x x x a x x x +-+++=-+-只有一个实数根,则符合条件的所有实数a 的值的总和为( ) A .6- B .30- C .32- D .38- 4.如图,在ABC △中,6AB =,3BC =,7CA =,I 为ABC △的内心,连接CI 并延长交AB 于点D 。记CAI △的面积为m , DAI △的面积为n ,则 m n =( ) A .32 B .43 C .53 D .74 5.已知x ,y 为实数,且满足2244x xy y -+=,记224u x xy y =++的最大值为M ,最小 A B C D I 2 值为m ,则M m +=( ) A .403 B .64 15 C .13615 D .315 二、填空题(共5小题,每小题7分,共35分) 6.在平面直角坐标系内有两点(11)A ,,(23)B ,,若一次函数2y kx =+的图像与线段AB 有公共点,则k 的取值范围为 。 7.如图,在ABC △中,D 为BC 边上一点,E 为线段AD 上一点,延长BE 交AC 于点F 。若 25BD BC =,12AE AD =,则AF AC = 。 8.设1x ,2x ,3x ,…,n x 是n 个互不相同的正整数,且1232017n x x x x ++++=L ,则n 的最大值是 。 9.如图,AB 是O ⊙的直径,AC 是O ⊙的切线,BC 交O ⊙于E 点,若 OA CE =,则AE AB = 。 E O A B C F B C A D E 五年级数学竞赛试卷及答案 一、填空(共28分,每空2分) 1. 两个数的和是61.6,其中一个数的小数点向右移动一位,就与另一个数相 同。两个数分别是( )、( )。 2. 有三根木料,打算把每根锯成3段,每锯开一处需要3分钟,全部锯完需要 ( )分钟。 3. 笑笑同学的家住在5楼,每层楼梯有16级,她从1楼走到5楼, 共要走()级楼梯。 4. 把一张边长24厘米的正方形纸对折4次后得到一个小正方形,这个小正方 形的面积是()平方厘米。 5. 李师傅3小时生产96个零件,照这样计算生产288个零件要() 6. 一个长方形的长为9厘米,把它的长的一边减少3厘米,另一边不变,面积就减少9平方厘米,这时变成的梯形面积是()平方厘米。 7. 小明和小英两人同时从甲、乙两地相向而行,小明每分钟行a米,小英每分 钟行b米,行了4分钟两人相遇。甲、乙两地的路程是( )米。 8.哥哥7年前的年龄和妹妹5年后的年龄相等,当哥哥()岁时,正好是妹妹年龄的3倍。 9.按规律在括号里填数。 (1)1、3、7、15、31、()、()。 (2)2、8、5、20、7、28、11、44、()、12。 (3)1,1,2,3,5,8,(),21。 10. 五(1)班的同学去划船。他们算了一下,如果增加一条船,正好每条船坐6 人;如果减少一条船,正好每条船坐9人。这个班共有()名同学。 二、判断(正确的在括号里画“√”,错误的画“×”。共15分,每小题3分) 11. 用10张同样长的纸条接成一条长31厘米的纸带,如果每个接头都重叠1 厘米,那么每张纸条长4.1厘米。( ) 12. 用三个长3厘米、宽2厘米,高1厘米的长方体,拼成一个大长方体,有3 种拼法。() 13. 把一批圆木自上而下按1、2、3……14、15根放在一起,这批圆木共有240 根。 () 14. 在a÷b=5……3中,把a、b同时扩大3倍,商是5,余数是3。( ) 15. 右图中长方形的面积与阴影部分 的面积相等。() 三、选择(把正确答案的序号填在括号里。共12分,每小题3分) 16. “IMO”是国际数学奥林匹克竞赛的缩写,如果要把这三个字母写成三种不 同的颜色,现有五种不同的颜色,按上述要求可以写出()种不同颜色搭配的“IMO”。 A . 15 B. 20 C. 45 D. 60、 17.五(2)班有56个学生,在一次测验中,答对第一题的34人,答对第二题的29人,两题都答对的15人。那么,两题都不对的有()人。 A. 7 B. 8 C.12 D. 20 A. 6 B. 7 C. 8 D. 9 19. 小刘、小张和小徐在一起,一位是工人,一位是农民,一位是战士。现在只知道:(1) 小徐比战士年龄大;(2)小刘和农民不同岁;(3)农民比小张年龄小;那 么,( )工人。2018七年级上数学竞赛试题
历届“大梦杯”福建省初中数学竞赛试题及答案
五年级上册数学竞赛试卷及答案
