第四章 习题解

第四章 习题解

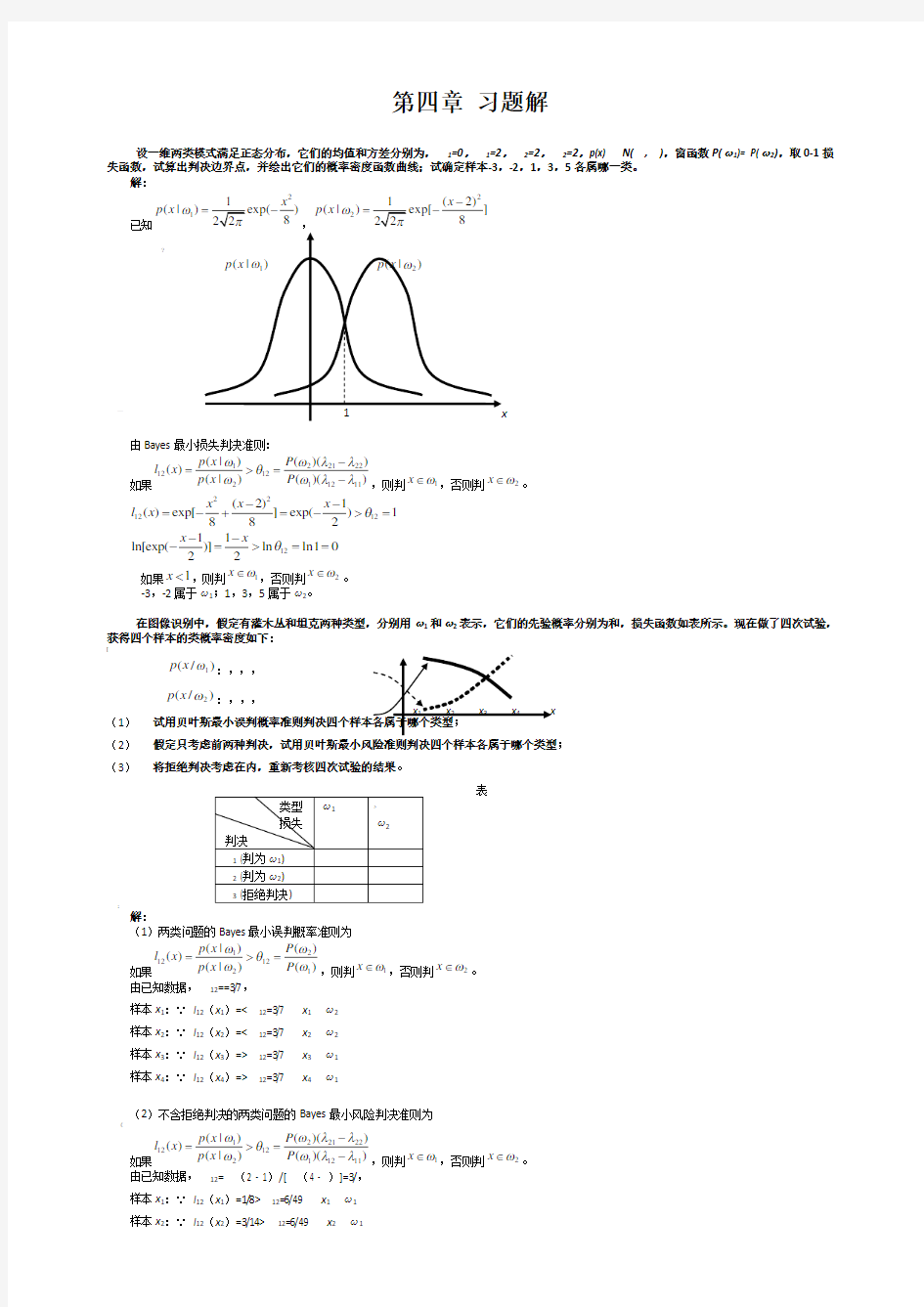
设一维两类模式满足正态分布，它们的均值和方差分别为，1=0，1=2，2=2，2=2，p(x) N(,)，窗函数P(ω1)= P(ω2)，取0-1损失函数，试算出判决边界点，并绘出它们的概率密度函数曲线；试确定样本-3，-2，1，3，5各属哪一类。 解： 已知211(|)exp()822x p x ωπ=-2

21(2)(|)exp[]822x p x ωπ-=-

?

1(|)p x ω 2(|)p x ω

—

由Bayes 最小损失判决准则： 如果1221221212211211(|)()()()(|)()()p x P l x p x P ωωλλθωωλλ-=

>=-，则判1x ω∈，否则判2x ω∈。

221212(2)1()exp[]exp()1882x x x l x θ--=-+=->=

1211ln[exp()]ln ln1022x x θ---=>==

如果1x <，则判

1x ω∈，否则判2x ω∈。 -3，-2属于ω1；1，3，5属于ω2。

在图像识别中，假定有灌木丛和坦克两种类型，分别用ω1和ω2表示，它们的先验概率分别为和，损失函数如表所示。现在做了四次试验，获得四个样本的类概率密度如下：

[

)/(1ωx p ：，，，

)/(2ωx p ：，，， （1） 试用贝叶斯最小误判概率准则判决四个样本各属于哪个类型；

（2） 假定只考虑前两种判决，试用贝叶斯最小风险准则判决四个样本各属于哪个类型；

（3） 将拒绝判决考虑在内，重新考核四次试验的结果。

表

类型 损失

判决

ω1

> ω2 1 (判为ω1)

2 (判为ω2)

3 (拒绝判决)

: 解：

（1）两类问题的Bayes 最小误判概率准则为

如果

12121221(|)()()(|)()p x P l x p x P ωωθωω=

>=，则判1x ω∈，否则判2x ω∈。 由已知数据，12==3

/7， 样本x 1：∵ l 12（x 1）=<12=3

/7 x 1ω2 样本x 2：∵ l 12（x 2）=<12=3

/7 x 2ω2 样本x 3：∵ l 12（x 3）=>12=3

/7 x 3ω1 样本x 4：∵ l 12（x 4）=>

12=3/7 x 4ω1 （2）不含拒绝判决的两类问题的Bayes 最小风险判决准则为

《 如果

1221221212211211(|)()()()(|)()()p x P l x p x P ωωλλθωωλλ-=

>=-，则判1x ω∈，否则判2x ω∈。

由已知数据，12=（2 - 1）/[（4 - ）]=3/，

样本x 1：∵ l 12（x 1）=1/8>12=6/49 x 1ω1

样本x 2：∵ l 12（x 2）=3/14>12=6/

49 x 2ω1 1

x

x 1 x 2 x 3 x 4 x

样本x 3：∵ l 12（x 3）=6/11>

12=6/49 x 3ω1 样本x 4：∵ l 12（x 4）=6/3>12=6/49 x 4ω1

（3）含拒绝判决的两类问题的Bayes 最小风险判决准则为

1,2,3if (|)min[(|)] then , 3i j i j R x R x x i ααω==∈=时为拒绝判决

^ 其中条件风险：

2

1(|)(|)(|),1,2,3j j i i i R x P x j αλαωω===∑ 后验概率： 21(|)(|)()/()(|)()/[(|)()]

i i i i i i i i P x p x P p x p x P p x P ωωωωωωω===∑

2

11(|)(|)(|)(),1,2,3()j j i i i i R x p x P j p x αλαωωω===∑

记21(|)(|)(|)(),1,2,3j j i i i i r x p x P j αλαωωω===∑

则，含拒绝判决的两类问题的Bayes 最小风险判决准则为 1,2,3if r(|)min[(|)] then , 3i j i j x r x x i ααω==∈=时为拒绝判决

对四个样本逐一列写下表，用式计算r (j |x )。

样本x 1：

(j |ωi ) 类型 > 损失

判决

ω1 p (x |ω1)P (ω1)= = ω2 p (x |ω2)P (ω2)= =

r (

j |x ) ) 1 (判为ω1)

*+2*= 2 (判为ω2)

4*+1*= 3 (拒绝判决) ？

*+*=

因为r (3|x 1)=最小，所以拒绝判决；

样本x 2：

(j |ωi ) 类型 损失 判决

ω1 p (x |ω1)P (ω1)= ) = ω2 p (x |ω2)P (ω2)= =

r (j |x )

1 (判为ω1)

￥ *+2*=

2 (判为ω2)

4*+1*= 3 (拒绝判决)

*+*= 因为r (1|x 2)=最小，所以判x 2

ω1，即灌木丛，或拒绝判决； ~ 样本x 3：

(j |ωi ) 类

型

损失

判决

ω1 p (x |ω1)P (ω1)= = ω2 p (x |ω2)P (ω2)= = [ r (j |x ) 1 (判为ω1)

*+2*= 2 (判为ω2)

| 4*+1*=

3 (拒绝判决)

*+*= 因为r (1|x 3)=最小，所以判x 3

ω1，即灌木丛； 4：

(j |ωi ) 类型 损失 判决

}

ω1

p (x |ω1)P (ω1)=

= ω2 p (x |ω2)P (ω2)= = r (j |x ) 1 (判为ω1) ，

*+2*= 2 (判为ω2)

4*+1*= 3 (拒绝判决)

.

*+*= 1441

假设两类二维正态分布参数为1=(-1，0)’，2=(1，0)’，先验概率相等。

（1）令1=2=I ，试给出负对数似然比判决规则；

（2）令

111/21/21??∑= ??? 211/21/2

1-??∑= ?-?? 试给出负对数似然比判决规则。 解： Bayes 最小误判概率似然比判决规则为 … 如果12121221(|)()()1(|)()p x P l x p x P ωωθωω=

>==，则判1x ω∈，否则判2x ω∈。 相应的负对数似然比判决规则为

如果122112ln ()ln (|)ln (|)ln ln10l x p x p x

ωωθ-=-<-=-=，则判1x ω∈，否则判2x ω∈。

对于正态分布

1/21/21

1(|)exp[()'()](2)||2i i i i n i p x x x ωμμπ-=--∑-∑ 1112121112221ln ()[ln ||ln ||()'()()'()]2l x x x x x μμμμ---=∑-∑+-∑---∑-

（1）由已知，

22111212211(1)111(|)exp[()'()]exp[]002222x x x x p x I x x ωππ--????????++=---=- ? ? ? ?????

????22111222211(1)111(|)exp[()'()]exp[]002222x x x x p x I x x ωππ????????-+=---=- ? ? ? ?????????

221221111ln ()ln (|)ln (|)(1)(1)4l x p x p x x x x ωω-=-=+--=

故，如果

10x <则判1x ω∈，否则判2x ω∈。

（2） ∵

111/2||3/41/21∑=

=， 21

1/2||3/4

1/21-∑==-

@ 11

111/211/241/211/213---????∑== ? ?-??

??，21111/211/241/211/213---????∑== ? ?-???? ''

1111122222111111/211/21414ln ()1/211/212323x x x x l x x x x x ++---????????????-=- ? ? ? ? ? ?-???????????? '

'1212111122221/21/21122113322x x x x x x x x x x x x +--+????+-???? ? ?=-+- ? ? ? ?-++ ? ?????????

111122*********[(1)(1/2)()(1)(1/2)()]322x x x x x x x x x x x x +-=++-+-+---+-+

1124(2)3x x x =-

1212if (2)0 then else x x x x ωω-<∈∈ 即，121212if [(<0)and( 2)][(0)and( 2)] then else x x or x x x x ωω<>>∈∈

{

补充题1：

假设两类一维模式的概率密度函数为

10.51, 02(|)0, x x p x ω-+≤≤?=??其它 20.50.5, 13(|)0, x x p x ω-≤≤?=??其它

先验概率相等。 （1）求Bayes 判决函数（用0-1损失函数）； " （2）求总的误判概率。

解：（1）

当用0-1损失函数且先验概率相等时，Bayes 最小损失判决规则为： 如果122122211211(|)()1(|)()p x P p x P ωωλλωωλλ->=-（）（），则判

1x ω∈，否则判2x ω∈。 即，

12(|)(|)p x p x ωω>，则判1x ω∈，否则判2x ω∈。 代入本题类概率密度函数得：

如果x <，则判x ω1，否则判x ω2。

故，Bayes 判决函数为d(x)= 。

^

（2）误判概率 211112()()(|)()(|)P e P p x dx P p x dx

ωωωωΩΩ=+??

2 1.51.51111()(0.51)(0.50.5)228P e x dx x dx =

-++-=??

补充题2：

在目标识别中，假定类型1为敌方目标，类型2为诱饵（假目标），已知先验概率P(1)=和P(2)=，类概率密度函数如下：

1, 01(|)2, 12

0, x x p x x x ω≤

其它 11, 12(|)3, 230, x x p x x x ω-≤

（2）求总错误概率P(e)； （3）假设正确判断的损失11=22=0，误判损失分别为12和21，若采用最小损失判决准则，

12和21满足怎样的关系时，会使上述对x=的判断相反 解：（1）应用贝叶斯最小误判概率准则如果 )()()(2112ωω=x p x p x l <>)()(12ωωP P 则判 ???ωω∈21x 得 l 12=1 < )()(12ωωP P =4，故 x=属于 2 。 （2）P(e)= 212121)()()(εω+εω=P P e P ??ΩΩωω+ωω=12)()()()(2211x

d x p P x d x p P

=dx x x x ??-+- 1.2

121.210.8d )2(0.2）（=

(3) 两类问题的最小损失准则的似然比形式的判决规则为： 如果 ))(())(()()(111212221221λ-λωλ-λω<>ωωP P x p x p

则判

???ωω∈21x 带入x=得到

12≥421 0 1 2 3 x 1 p(x|ω1) ，