基于MATLAB的可行方向法求极值问题讲解

基于MATLAB 可行方向法求极值的实现

姓名：xxx

学号：xxx

（北京理工大学机械与车辆学院车辆工程，北京 100081）

摘要：在工程实际的优化设计中，随着设计变量数和约束条件数的增加，随机方向搜索法和复合形法等直接优化解法的求解效率会偏低。可行方向法，顾名思义，一种始终在可行域内寻找下降方向的搜索法，以其收敛速度快、效果好的优点已成为求解约束非线性问题的一种有代表性的直接解法，同时也是求解大型约束优化问题的主要方法之一。本文将简单介绍可行方向法的数学思想，采用线性规划法和约束最优步长法编写MATLAB 程序，最后通过算例完成对优化问题的求解。 关键字：可行方向法；MATLAB ；优化方法。

1. 可行方向法的基本数学思想

1.1可行方向法的搜索策略

可行方向法迭代的第一步都是从可行域的某一初始点(0)X 出发，沿负梯度

(0)()f X -?方向移至某一个或J 个起作用约束面的交集()k X 上。以后的搜索路线和迭代计算可根据约束函数和目标函数的不同性状，分别采用以下三种不同策略继续搜索。

1）

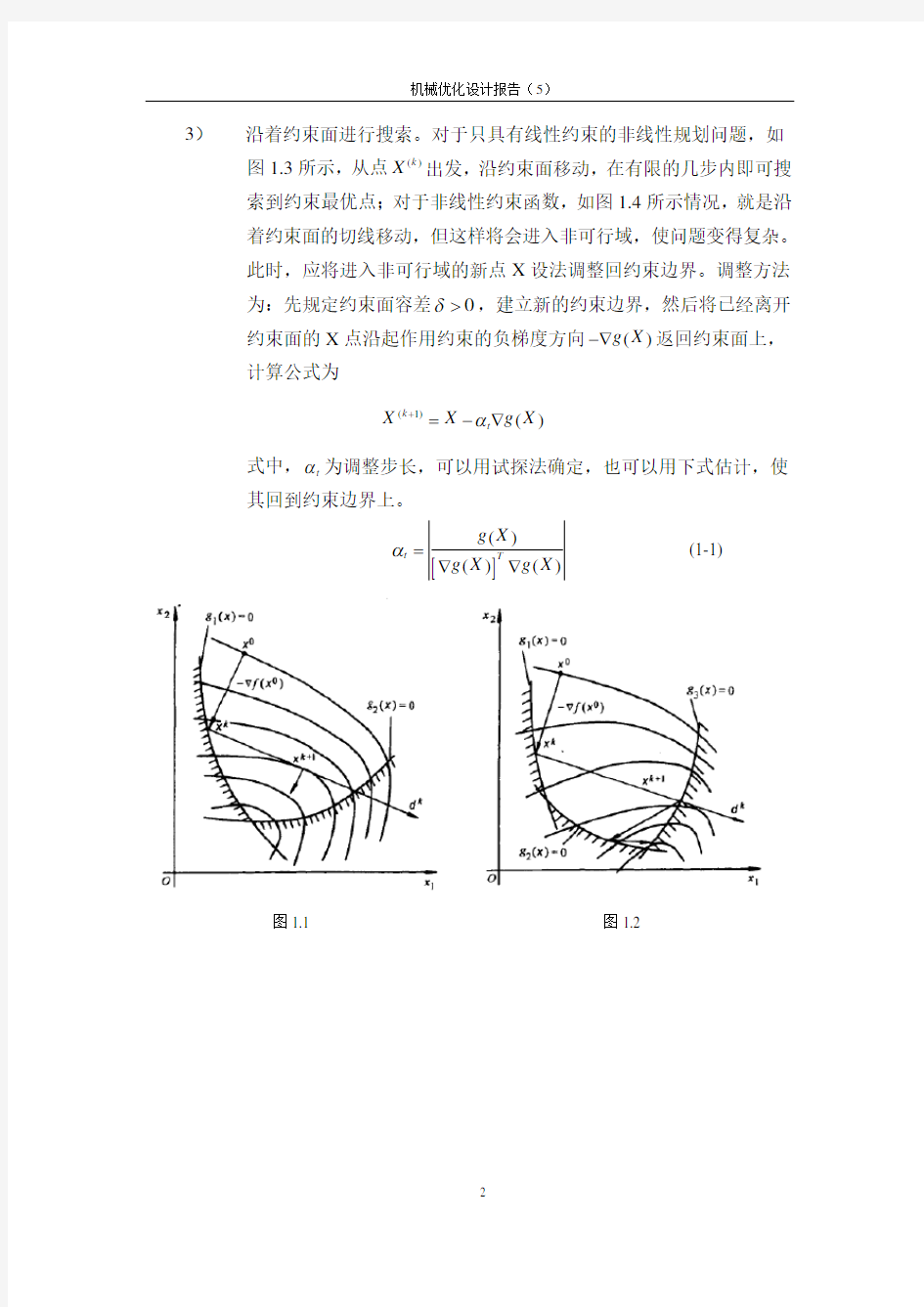
由点()k X 出发，沿可行方向作一维最优化搜索，若所得新点(1)k X +在可行域内，则再沿(1)()k f X +-?方向作一维最优化搜索；若所得的新点不在可行域内，则将它移至约束面上再反复重复上述步骤，若

(1)()k f X ε+?≤，则停止迭代，如图1.1所示。

2）

由点()k X 出发，沿可行方向作一维最优化搜索，若所得新点(1)k X +在可行域外，则沿可行方向以最大步长到达另一个约束面上一点，将该点作为迭代点(1)k X +进行反复搜索，直至满足给出的K-T 条件，如图1.2所示。

3） 沿着约束面进行搜索。对于只具有线性约束的非线性规划问题，如图1.3所示，从点()k X 出发，沿约束面移动，在有限的几步内即可搜索到约束最优点；对于非线性约束函数，如图1.4所示情况，就是沿着约束面的切线移动，但这样将会进入非可行域，使问题变得复杂。此时，应将进入非可行域的新点X 设法调整回约束边界。调整方法为：先规定约束面容差0δ>，建立新的约束边界，然后将已经离开约束面的X 点沿起作用约束的负梯度方向()g X -?返回约束面上，计算公式为

(1)()k t X X g X α+=-?

式中，t α为调整步长，可以用试探法确定，也可以用下式估计，使其回到约束边界上。

[]

()

()()

t T

g X g X g X α=

?? (1-1)

图1.1

图1.2

图1.3

图1.4

不管采用哪种搜索方法都要进行两条决策：一是产生一个适用的可行方向()k d ；二是沿()

k d 方向确定一个不会越出可行域的适当的步长因子。

1.2产生可行方向和步长的数学原理

可行方向要保证沿该方向作微小移动后所得的新点是可行点，且目标函数值有所下降。显然可行方向应满足可行和下降两个条件。这里从数学原理的角度分析可行性和下降性。

1.2.1可行性

设()

k X 为可行域D 中的一个点，即()

k X D ∈。对于某一方向()

k d 来说，若存

在数00A >，使其对于任意的A 0(0)A A ≤≤，式1-2均成立，则称方向()

k d 对()

k X 点满足可行性条件。

()

()

k k X

Ad D +∈ （1-2）

若点()k X 在可行域内，即()k X 为内点，则任何方向都满足可行性条件。 当点()k X 在某一约束边界上时，如图1.5所示，该约束面就是起作用约束。当点()k X 位于一个约束面上时，如图1.6所示，作出()k X 初起作用约束的梯度

()g X ?和切线，可见只要()

k d 与起作用约束的梯度成直角或钝角，则可指向可行

域内，满足可行性条件。当()k X 同时处于J 个约束面时，就要求()

k d 与这J 个约束面的梯度均垂直或交成钝角，如图1.6所示，写成数学表达式如下：

()()

()0(1,2,,)T k k j g X d j J ???≤=?? 式中，J 为起作用约束的个数。上式称为可行性条件。

图1.5

图1.6

1.2.2下降性

沿一方向搜索时，要求下降愈快愈好。对某一点来说，负梯度方向为最速下降方向。如果负梯度方向是可行方向，那么负梯度方向是最有利的方向；否则为

了保证目标函数值有所下降，至少要使搜索方向()

k d 与目标函数的负梯度方向成锐角或与梯度方向成钝角，写成数学表达式为

()()

()0T k k f X d ???

该式称为下降性条件。

如图1.7所示，可行下降方向显然位于点()k X 约束面的切线与目标函数等值线的切线所围成的扇形区域内，推广到一般的情况就是可行方向在目标函数超等值面的超切面和J 个起作用约束的超切面所围成的超锥体内。该区域称为可行下降方向区。

图1.7

综上所述，当点()k X 位于J 个起作用的约束面上时，满足

()()()()

()0(1,2,,)()0

T k k j T k k g X d j J f X d ????≤=???

??

???

（1-3） 式中，()

k d 即为可行方向。

1.3可行方向的产生

本文采用线性规划法来产生可行方向，用约束最优步长确定最优步长，为后面编制MATLAB 程序做理论基础。本节先阐述线性规划法，下节再对约束最优步长法进行描述。

线性规划法对包含线性和非线性的不等式约束的最优化问题都适用，但不允许有等式约束。其基本原理是将具有一阶连续偏导数的目标函数和约束条件在

()k X 点用Taylor 展开式展成线性近似函数（一次项），并用这些线性近似函数代

替目标函数和它的约束条件，使得问题线性化。这样min ()f X 成为

()()()min{()[()]()}()k k T k n f X f X X X X R +?-∈

约束条件()0u g X ≤变为

()()()()[()]()0(1,2,,)k k T k u u g X g X X X u m +?-≤=

用(1)k X +代替上式中的X ，得到

()()

()

min{()[()]}k k k T

k f X

f X

d α+?

s.t. ()

()()()[()]0(1,2,,)k k k T u k u g X g X d u m α+?≤=

式中，()

()k f X

、()

()k u g X

为常数，只有搜索方向()

k d 和k α是未知量。当迭

代点()k X 位于J 个起作用约束边界的交点上时，问题就变成求解线性规划问题：

()

()min[()]n

k k T X R

f X d ∈? s.t. ()

()

[()]0(1,2,,J)k k T

u g X

d u ?≤=

式中，()k d 只起到方向作用，故规定其向量的模是有界的，也就是规定()

k d 每个分量的绝对值不大于1，即

()

j ||1(1,2,,)k d j n ≤=

由于可行方向还得满足式1-3的可行性和下降性条件，故确定可行方向的线性规划数学模型如下：

()()

()min ()[()]n

k k k T X R

Z d f X d ∈=? s.t. ()

()

[()]0k k T

f X

d ?<

()

()

[()]0(1,2,,J)k k T

u g X

d u ?≤=

()

j 11(1,2,,)k d j n -≤≤= (1-4)

求解后，可得到迭代方向()

k d ，作为下一步的搜索方向。

1.4最优步长的确定

由线性规划法求的可行方向()

k d 后，由()k X 出发，找到该方向上的可行新点

(1)k X +。新点必须满足两个条件，一是新点(1)k X +必须还是可行点，二是目标函

数值具有最大的下降量。约束最优步长即可满足这两点，可用以下一维搜索法求

解：

()()

min ()k k f X

d α

α+

s.t. max 0αα≤≤

式中，()

()

max sup{|()0(1,2,,)}k k u g X

d u m αλα=+≤= 。

2. 可行方向法的迭代过程和算法流程图

2.1迭代过程

1)输入收敛精度ε；

2)形成可行初始点(0)X ，令k=1;

3)确定起作用约束下标集合，()()(){|()0(1)}k k i E X i g X i m ==≤≤； 4)判断E 是否为空集，若是空集则说明()k X 在可行域内，转步骤5）；否则说明()k X 在约束边界上，转步骤6)；

5)判断是否满足终止条件()()k f X ε?≤，若满足，转步骤10)；若不满足，

则取搜索方向为()

()()k k d f X =-? ，转步骤8)；

6)采用线性规划法，用式1-4求解后，得到可行方向()

k d ；

7)判断0k Z =是否成立，若成立，则转步骤10)输出，停机结束；若不成立，则继续下一步；

8)采用约束最优步长法进行一维搜索，得到新点(1)k X +; 9)令k=k+1，转步骤3)；

10)输出*()k X X =，**()f f X =，停机结束。

2.2算法流程图

算法流程图如图2-1。

图2-1 可行方向法的算法流程图3.可行方向法的MATLAB程序

function kxfxf(x0)

eps=1.0e-6;

%刚开始给的x0为行向量

x0=transpose(x0);

func

sz=length(x0);

G1 = G;

for k=1:1:50

%'f(x)梯度：'

sf=diff_val(x0);

sf=eval('sf');

%'f(x)梯度范数：'

norm_s=norm(diff_val(x0));

GL=length(G);

G1 = G;

G_copy=G;

for i=1:1:GL

g=subs(G1(i,:),x,x0);

G1(i,:)=g;

end

G_zero=eval('G1');

for i=GL:-1:1

if abs(G_zero(i,:))>0.1

G_zero(i,:)=[];

G_copy(i,:)=[];

end

end

I=size(G_zero,1);

add=-ones(I,1);

%根据E是否为空集(I==0)确定不同情况下的搜索方向

if I==0

if norm_s<=3

'最优解：'

'自变量值:'

x0

'目标函数值：'

f=fval(x0)

'迭代次数：'

k

'======================================================' return

else

d0=-diff_val(x0);

%线性搜索

d0=transpose(d0);

vmax = gmin(x0,d0);

h=fmin(x0,d0,vmax);

x0=x0+h*d0;

end

else

%线性规划

grad=jacobian(G_copy,x);

G_zero=subs(grad,x,x0);

Ac=[sf;G_zero];

lb=-1*ones(sz,1);

ub=ones(sz,1);

p=zeros(I+1,1);

dz = size(1,sz);

c=sf*dz';

[dz,mn,m1,m2,m3]=linprog(c,Ac,p,[],[],lb,ub);

z0 = sf*dz;

z0=abs(z0);

if z0<0.01

'最优解：'

'自变量值:'

x0

'目标函数值：'

f=fval(x0)

'迭代次数：'

k

'======================================================'

return

else

d0=dz;

%线性搜索

vmax = gmin(x0,d0);

h=fmin(x0,d0,vmax);

x0=x0+h*d0;

end

end

end

程序中用到一些回调函数，简单列举如下，.m文件详细内容见附录一。func记录函数及其自变量信息

fval(x0)计算函数在x0处得函数值

最小值

gmin(x0,d0) 求函数在满足约束条件下的

k

fmin(x0,d0,vmax)求函数在[0,vmax]上的最小值

diff_val(x0)计算函数在x0处得导数值。

4.利用MATLAB 求解实例

4.1实例

本文以课本例题5.3为例来验证可行方向法在MATLAB 里的实现。

已知目标函数2

12()412f X x x =+-，约束条件为 s.t. 22112()250g X x x =+-≤

22()0g X x =-≤ 31()0g X x =-≤

初始点为(0)32X ??

=????，求()f X 的极小值，计算精度210ε-=。

首先在func.m 文件中输入目标函数和约束条件，如下： f=4*x1+x2^2-12; g1=x1^2+x2^2-25; g2=-x2; g3=-x1; G = [g1;g2;g3];

在MATLAB 命令窗口里输入如下命令： >> x0=[3 2] >> kxfxf(x0) 计算结果为：

最优解： 自变量值: x0 =

1.0e-03 *

0.066121027424648 0.212777459551459 ans = 目标函数值： f =

-11.999735470616054 ans = 迭代次数： k = 3

与书中提供的精确解基本一致，最优解的相对误差为

11.9997(12)

100%

0.0025%

11.9997

---?=-， 说明此方法有效可行。 4.2实例结果分析

此处主要从以下三个方面来分析此算法及计算结果。 1) 可靠性。

通过对其他多元多次函数（教科书例5.1）进行求极值计算，结果都比较精确，说明此算法可靠性、通用性好。通过对教课书例5.1进行求解，可得以下结果：

x0 =

6.000146685451760 6.999853314348210 目标函数值： f =

2.000586785240415 迭代次数： k =

3

与课本上精确解相比，几乎完全吻合。

2)有效性。

对于本例，目标函数不是很复杂，其求解速率在1s内可完成，迭代次数为k=3次。

3)简便性。

此程序逻辑清晰，简明易懂，对计算机的要求也不是很高，其简便性不言而明。

参考文献

[1]李志锋。机械优化设计。高等教育出版社。

[2]孙靖民。机械优化设计。机械工业出版社。1999.5。

[3]蒲俊，吉家锋，伊良忠。MATLAB 6.0数学手册。浦东电子出版社。2002.1。

附录一回调函数内容

1.func 记录函数及其自变量信息

根据所求解的目标函数和相应的约束条件不同而不同，由用户进行手动

输入。示例见4.1。

2.fval(x0) 计算函数在x0处得函数值

function f_val=fval(x0)

x0=transpose(x0);

func;

f_val=subs(f,x,x0);

最小值

3.gmin(x0,d0) 求函数在满足约束条件下的

k

function h=gmin(x0,d0)

syms h;

func

n = length(G);

alpha = zeros(1,n);

a=x0+h*d0;

g_val=subs(G,x,a);

k = 1;

for i=1:1:n

alpha_temp = solve(g_val(i));

if length(alpha_temp)>1

if imag(alpha_temp) == 0

for j=1:1:length(alpha_temp)

if alpha_temp(j,1)>0 || alpha_temp(j,1) == 0

alpha(1,k) = alpha_temp(j,1);

k = k+1;

end

end

else

end

else

if alpha_temp > 0 || alpha_temp == 0

alpha(1,k) = alpha_temp;

k = k+1;

else

alpha(:,k) = [];

end

end

end

h_temp = alpha(1,1);

len = length(alpha);

for i=1:1:len

if h_temp > alpha(1,i)

h_temp = alpha(1,i);

end

end

h=h_temp;

4.fmin(x0,d0,vmax)求函数在[0,vmax]上的最小值

function h=fmin(x0,d0,vmax)

func

syms h;

a=x0+h*d0;

f_val=inline(subs(f,x,a));

if vmax==inf

min_h=fminbnd(f_val,0,10000);

else

min_h=fminbnd(f_val,0,vmax);

end

h=min_h;

5.diff_val(x0)计算函数在x0处得导数值

function s=diff_val(x0)

func

grad=jacobian(f,x);

s=subs(grad,x,x0);