最新(整理)压杆稳定计算.

第16章压杆稳定

16.1 压杆稳定性的概念

在第二章中，曾讨论过受压杆件的强度问题，并且认为只要压杆满足了强度条件，就能保证其正常工作。但是，实践与理论证明，这个结论仅对4

短粗的压杆才是正确的，对细长压杆不能应用上述结论，因为细长压杆丧6

失工作能力的原因，不是因为强度不够，而是由于出现了与强度问题截然7

不同的另一种破坏形式，这就是本章将要讨论的压杆稳定性问题。

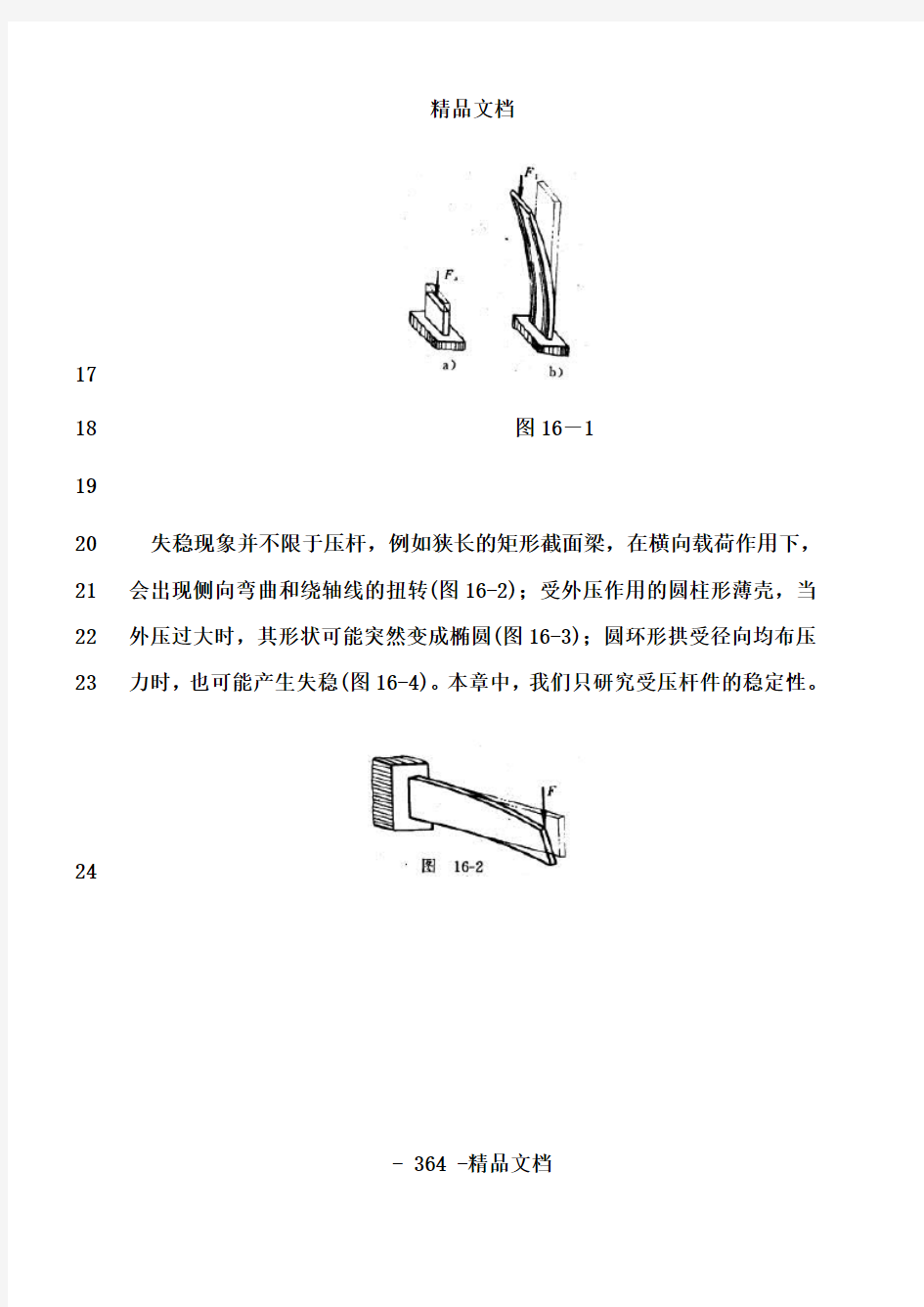
当短粗杆受压时(图16-1a)，在压力F由小逐渐增大的过程中，杆件始9

终保持原有的直线平衡形式，直到压力F达到屈服强度载荷F s(或抗压强度载荷F b)，杆件发生强度破坏时为止。但是，如果用相同的材料，做一根

与图16-1a所示的同样粗细而比较长的杆件(图16-1b)，当压力F比较小12

时，这一较长的杆件尚能保持直线的平衡形式，而当压力F逐渐增大至某13

—数值F1时，杆件将突然变弯，不再保持原有的直线平衡形式，因而丧失14

了承载能力。我们把受压直杆突然变弯的现象，称为丧失稳定或失稳。此15

时，F1可能远小于F s(或F b)。可见，细长杆在尚未产生强度破坏时，就因失稳而破坏。

- 363 -精品文档

图16－1

失稳现象并不限于压杆，例如狭长的矩形截面梁，在横向载荷作用下，

会出现侧向弯曲和绕轴线的扭转(图16-2)；受外压作用的圆柱形薄壳，当外压过大时，其形状可能突然变成椭圆(图16-3)；圆环形拱受径向均布压

力时，也可能产生失稳(图16-4)。本章中，我们只研究受压杆件的稳定性。

- 364 -精品文档

- 365 -精品文档

图16-3 25

所谓的稳定性是指杆件保持原有直线平衡形式的能力。实际上它是指平27

衡状态的稳定性。我们借助于刚性小球处于三种平衡状态的情况来形象地28

加以说明。 29

第一种状态，小球在凹面内的O 点处于平衡状态，如图16-5a 所示。先30

用外加干扰力使其偏离原有的平衡位置，然后再把干扰力去掉，小球能回31

到原来的平衡位置。因此，小球原有的平衡状态是稳定平衡。 32

第二种状态，小球在凸面上的O 点处于平衡状态，如图16-5c 所示。当33

用外加干扰力使其偏离原有的平衡位置后，小球将继续下滚，不再回到原34

来的平衡位置。因此，小球原有的干衡状态是不稳定平衡。 35

第三种状态，小球在平面上的O 点处于平衡状态，如图16-5b 所示，当36

用外加干扰力使其偏离原有的平衡位置后，把干扰力去掉后，小球将在新37

的位置O 1再次处于平衡，既没有恢复原位的趋势，也没有继续偏离的趋势。

因此。我们称小球原有的平衡状态为随遇平衡。

图16-5

图16-6

通过上述分析可以认识到，为了判别原有平衡状态的稳定性，必须使研47

究对象偏离其原有的平衡位置。因此。在研究压杆稳定时，我们也用一微48

小横向干扰力使处于直线平衡状态的压杆偏离原有的位置，如图16-6a所49

示。当轴向压力F由小变大的过程中，可以观察到：

1)当压力值F1较小时，给其一横向干扰力，杆件偏离原来的平衡位置。

若去掉横向干扰力后，压杆将在直线平衡位置左右摆动，最终将恢复到原

- 366 -精品文档

来的直线平衡位置，如图16-6b所示。所以，该杆原有直线平衡状态是稳

定平衡。

2)当压力值F2超过其一限度F cr时，平衡状态的性质发生了质变。这时，

只要有一轻微的横向干扰，压杆就会继续弯曲，不再恢复原状，如图16-6d

所示。因此，该杆原有直线平衡状态是不稳定平衡。

3)界于前二者之间，存在着一种临界状态。当压力值正好等于F cr时，58

一旦去掉横向干扰力，压杆将在微弯状态下达到新的平衡，既不恢复原状，59

也不再继续弯曲，如图16-6c所示。因此，该杆原有直线平衡状态是随遇60

平衡，该状态又称为临界状态。

临界状态是杆件从稳定平衡向不稳定平衡转化的极限状态。压杆处于临

界状态时的轴向压力称为临界力或临界载荷，用F cr表示。

由上述可知，压杆的原有直线平衡状态是否稳定，与所受轴向压力大小64

有关。当轴向压力达到临界力时，压杆即向失稳过渡。所以，对于压杆稳65

定性的研究，关键在于确定压杆的临界力。

16.2 两端铰支细长压杆的临界力

图16-7a为一两端为球形铰支的细长压杆，现推导其临界力公式。

- 367 -精品文档

- 368 -精品文档

图16-7 69

根据前节的讨论，轴向压力到达临界力时，压杆的直线平衡状态将由稳70

定转变为不稳定。在微小横向干扰力解除后，它将在微弯状态下保持平衡。71

因此，可以认为能够保持压杆在微弯状态下平衡的最小轴向压力，即为临72

界力。 73

选取坐标系如图l6-7a 所示，假想沿任意截面将压杆截开，保留部分如74

图16-7b 所示。由保留部分的平衡得 75

()v F x M cr -= (a) 76

在式(a)中，轴向压力F cr 取绝对值。这样，在图示的坐标系中弯矩M 与

- 369 -精品文档挠度v 的符号总相反，故式(a)中加了一个负号。当杆内应力不超过材料比78 例极限时，根据挠曲线近似微分方程有 79 ()EI v F EI x M x v cr -==22d d (b) 80 由于两端是球铰支座，它对端截面在任何方向的转角都没有限制。因而，81 杆件的微小弯曲变形一定发生于抗弯能力最弱的纵向平面内，所以上式中82 的I 应该是横截面的最小惯性矩。令 83 EI F k cr =2 (c) 84 式（b ）可改写为 85 0d d 222=+v k x v (d) 86 此微分方程的通解为 87 kx C kx C v cos sin 21+= (e) 88 式中1C 、2C 为积分常数。由压杆两端铰支这一边界条件 89 0=x ，0=v (f) 90 l x =，0=v (g)

力学计算公式

? 常用力学计算公式统计一、材料力学： 1.轴力（轴向拉压杆的强度条件） σmax=N max/A≤[σ] 其中，N为轴力，A为截面面积 2.胡克定律（应力与应变的关系） σ=Eε或△L=NL/EA @ 其中σ为应力，E为材料的弹性模量，ε为轴向应变， EA为杆件的刚度（表示杆件抵抗拉、压弹性变形的能力） 3.剪应力（假定剪应力沿剪切面是均匀分布的） τ=Q/A Q 其中，Q为剪力，A Q为剪切面面积 4.静矩（是对一定的轴而言，同一图形对不同的坐标轴的静矩不同,如果参考轴通过图形的形心，则x c=0， y c=0，此时静矩等于零）对Z轴的静矩S z=∫A ydA=y c A 其中：S为静矩，A为图形面积，y c为形心到坐标轴的距离，单位为m3。 5.惯性矩 … 对y轴的惯性矩I y=∫A z2dA

其中：A为图形面积，z为形心到y轴的距离，单位为m4 常用简单图形的惯性矩矩形：I x=bh3/12，I y=hb3/12 圆形：I z=πd4/64 空心圆截面：I z=πD4（1-a4）/64，a=d/D （一）、求通过矩形形心的惯性矩 " 求矩形通过形心，的惯性矩I x=∫Ay2dA dA=b·dy，则I x=∫h/2-h/2y2（bdy）=[by3/3]h/2-h/2=bh3/12（二）、求过三角形一条边的惯性矩

I x=∫Ay2dA，dA=b x·dy，b x=b·（h-y）/h 》则I x=∫h0（y2b（h-y）/h）dy=∫h0（y2b –y3b/h）dy =[by3/3]h0-[by4/4h]h0=bh3/12 6.梁正应力强度条件（梁的强度通常由横截面上的正应力控制） σmax=M max/W z≤[σ] 其中：M为弯矩，W为抗弯截面系数。 7.超静定问题及其解法对一般超静定问题的解决办法是：（1）、根据静力学平衡条件列出应有的平衡方程；（2）、根据变形协调条件列出变形几何方程；（3）、根据力学与变形间的物理关系将变形几何方程改写成所需的补充方程。 8.抗弯截面模量

力学计算公式

力学计算公式 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】

常用力学计算公式统计一、材料力学： 1.轴力（轴向拉压杆的强度条件） σmax=N max/A≤[σ] 其中，N为轴力，A为截面面积 2.胡克定律（应力与应变的关系） σ=Eε或△L=NL/EA 其中σ为应力，E为材料的弹性模量，ε为轴向应变，EA 为杆件的刚度（表示杆件抵抗拉、压弹性变形的能力） 3.剪应力（假定剪应力沿剪切面是均匀分布的） τ=Q/A Q 其中，Q为剪力，A Q为剪切面面积 4.静矩（是对一定的轴而言，同一图形对不同的坐标轴的静矩不同,如果参考轴通过图形的形心，则 x c=0，y c=0，此时静矩等于零）对Z轴的静矩S z=∫A ydA=y c A 其中：S为静矩，A为图形面积，y c为形心到坐标轴的距离，单位为m3。 5.惯性矩对y轴的惯性矩I y=∫A z2dA 其中：A为图形面积，z为形心到y轴的距离，单位为 m4

常用简单图形的惯性矩矩形：I x=bh3/12，I y=hb3/12 圆形：I z=πd4/64 空心圆截面：I z=πD4（1-a4）/64，a=d/D （一）、求通过矩形形心的惯性矩求矩形通过形心，的惯性矩I x=∫Ay2dA dA=b·dy，则I x=∫h/2-h/2y2（bdy）=[by3/3]h/2-h/2=bh3/12 （二）、求过三角形一条边的惯性矩 I x=∫Ay2dA，dA=b x·dy，b x=b·（h-y）/h 则I x=∫h0（y2b（h-y）/h）dy=∫h0（y2b –y3b/h）dy =[by3/3]h0-[by4/4h]h0=bh3/12 6.梁正应力强度条件（梁的强度通常由横截面上的正应力控制） σmax=M max/W z≤[σ] 其中：M为弯矩，W为抗弯截面系数。 7.超静定问题及其解法对一般超静定问题的解决办法是：（1）、根据静力学平衡条件列出应有的平衡方程；（2）、根据变形协调条件列出变形几何方程；（3）、根据力学与变形间的物理关系将变形几何方程改写成所需的补充方程。8.抗弯截面模量 W x=I x/y c

(整理)压杆稳定计算.

第16章压杆稳定 16.1 压杆稳定性的概念在第二章中，曾讨论过受压杆件的强度问题，并且认为只要压杆满足了强度条件，就能保证其正常工作。但是，实践与理论证明，这个结论仅对短粗的压杆才是正确的，对细长压杆不能应用上述结论，因为细长压杆丧失工作能力的原因，不是因为强度不够，而是由于出现了与强度问题截然不同的另一种破坏形式，这就是本章将要讨论的压杆稳定性问题。当短粗杆受压时(图16-1a)，在压力F由小逐渐增大的过程中，杆件始终保持原有的直线平衡形式，直到压力F达到屈服强度载荷F s(或抗压强度载荷F b)，杆件发生强度破坏时为止。但是，如果用相同的材料，做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b)，当压力F比较小时，这一较长的杆件尚能保持直线的平衡形式，而当压力F逐渐增大至某—数值F1时，杆件将突然变弯，不再保持原有的直线平衡形式，因而丧失了承载能力。我们把受压直杆突然变弯的现象，称为丧失稳定或失稳。此时，F1可能远小于F s(或F b)。可见，细长杆在尚未产生强度破坏时，就因失稳而破坏。图16－1 失稳现象并不限于压杆，例如狭长的矩形截面梁，在横向载荷作用下，会出现侧向弯曲和绕轴线的扭转(图16-2)；受外压作用的圆柱形薄壳，当外压过大时，其形状可能突然变成椭圆(图16-3)；圆环形拱受径向均布压力时，也可能产生失稳(图16-4)。本章中，我们只研究受压杆件的稳定性。

图16-3 所谓的稳定性是指杆件保持原有直线平衡形式的能力。实际上它是指平衡状态的稳定性。我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。第一种状态，小球在凹面内的O点处于平衡状态，如图16-5a所示。先用外加干扰力使其偏离原有的平衡位置，然后再把干扰力去掉，小球能回到原来的平衡位置。因此，小球原有的平衡状态是稳定平衡。第二种状态，小球在凸面上的O点处于平衡状态，如图16-5c所示。当用外加干扰力使其偏离原有的平衡位置后，小球将继续下滚，不再回到原来的平衡位置。因此，小球原有的干衡状态是不稳定平衡。第三种状态，小球在平面上的O点处于平衡状态，如图16-5b所示，当用外加干扰力使其偏离原有的平衡位置后，把干扰力去掉后，小球将在新的位置O1再次处于平衡，既没有恢复原位的趋势，也没有继续偏离的趋势。因此。我们称小球原有的平衡状态为随遇平衡。图16-5 图16-6 通过上述分析可以认识到，为了判别原有平衡状态的稳定性，必须使研究对象偏离其原有的平衡位置。因此。在研究压杆稳定时，我们也用一微小横向干扰力使处于

压杆的稳定性验算

建筑力学行动导向教学案例教案提纲

模块七压杆稳定性 7.1压杆稳定的概念为了说明问题，取如图 7-2 (a)所示的等直细长杆，在其两端施加轴向压力 F ,使杆在直线状态下处于平衡，此时，如果给杆以微小的侧向干扰力，使杆发生微小的弯曲，然后撤去干扰力，贝9当杆承受的轴向压力数值不同时，其结果也截然不同。当杆承受的轴向压力数值 F 小于某数值 F cr 时，在撤去干扰力以后，杆能自动恢复到原有的直线平衡状态而保持平衡, (a)、(b)所示，这种原有的直线平衡状态称为稳定的平衡; 压力F 小于匚时，杆件就能够保持稳定的平衡，这种性能称为压杆具有稳定性；而当压 F cr 杆所受的轴向压力 F 等于或者大于 F cr 时，杆件就不能保持稳定的平衡而失稳。压杆经常被应用于各种工程实际中，例如脚手架立杆和基坑支护的支撑杆，均承受压力，此时必须考虑其稳定性，以免引起压杆失稳破坏。 7.2临界力和临界应力 7.2.1细长压杆临界力计算公式一一欧拉公式从上面的讨论可知，压杆在临界力作用下，其直线状态的平衡将由稳定的平衡转变为不稳定的平衡，此时，即使撤去侧向干扰力，压杆仍然将保持在微弯状态下的平衡。当然，如果压力超过这个临界力，弯曲变形将明显增大。所以，使压杆在微弯状态下保持平衡的最小的轴向压力, 即为压杆的临界压力。下面介绍不同约束条件下压杆的临界力计算公式。一、两端铰支细长杆的临界力计算公式一一欧拉公式设两端铰支长度为z 的细长杆，在轴向压力/ cr 的作用下保持微弯平衡状态，如图 7-3所示。杆在小变形时其挠曲线近似微分方程为: 图7-2 到某一数值匚时，即使撤去干扰力，杆仍然处于微弯形 F cr 状，不能自动恢复到原有的直线平衡状态，如图 7-2 (c)、 (d)所示，则原有的直线平衡状态为不稳定的平衡。如果力 F 继续增大，则杆继续弯曲，产生显著的变形，甚至发生突然破坏。上述现象表明，在轴向压力 F 由小逐渐增大的过程中，压杆由稳定的平衡转变为不稳定的平衡，这种现象称为压杆丧失稳定性或者压杆失稳。显然压杆是否失稳取决于轴向压力的数值，压杆由直线状态的稳定的平衡过渡到不稳定的平衡时所对应的轴向压力，称为压杆的临界压力或临界力，用表示 / cr 当压杆所受的轴向图7-2 如图7-2 图 7-1 F 逐渐增大当杆承受的轴向压力数值图7-1

压杆稳定性最新计算

停车库的受力分析计算一、停车状态如下图所示二、分析立柱受力并校核已知：立柱截面为环形，令钢管厚度﹩=(D-d)/2为20mm 即D-d=0.02,材料选为45#，屈服强度s σ≥355Mpa,安全系数n 取为1.5，弹性模量取为210Gpa ，泊松比取为0.26。解：简化模型如图1所示,显然Mx>My,故按照Mx 情况进行校核。板自重m1=500Kg ，小车自重为m2=2000Kg 。分析立柱受力知其受压力和弯矩（包含风载），故：需校核其强度即，[]σσ≤ 1、起升载荷Q 的确定起升载荷包括允许起升的最大汽车重量、以及载车板，因起升高度＜50米，故钢丝绳质量不计。因起升速度≤R v 0.2m/s,故起升载荷动载系数2?05.1min ==? 故，()2221m ???+=?=g m Q F 2、风载荷W P 的确定 qA CK P W h = C ——风力系数，用以考虑受风结构物体型、尺寸等因素对风压的影响 h K ——风力高度变化系数 q ——计算风压() 2/m N A ——立柱垂直于风向的迎风面积() 2m 正视图左视图

1）计算风压q 风压计算公式为 2613.0q v = 风压按照沿海地区工作状态风压计算v=20m/s,故q=245.22 m /N 风压按照工作状态下的最大计算风压计算，此时q 取2502m /N ，故最终q 取250 2m /N 。 2）风力系数C 因为离地面高度≤10m,按照海上及海岛2 .010?? ? ??h ，风压高度变化系数h K 取1.00 因为是圆管结构且10q 2≈d （q 为计算风压，d 为圆管直径），故C 取0.9 3）迎风面积A t A A ψ= ψ——结构的充实率，t A A = ψ，钢管桁架结构ψ值取0.2-0.4，故0.3 t A ——结构或物品外形轮廓面积在垂直于风向平面上的投影() 2m h D A t =() 2m D ——立柱外径；h ——立柱高度 D D qA CK P W 675 325000.19.0h =????== 3、强度校核1 []n s σσσ= ≤ 即[]σσ≤+= W M A F max cmax 令W M A F + = σ 2??=Q F ;()g m m Q 21+= () 22 4 d D A -= π 21M M M += M1——由重力引起的弯矩；M2——由风载引起的弯矩 ()3.121m 1?+=g m M ;h P M W *=2 1 2

!第八章压杆稳定性

15-1 两端为球铰的压杆，当它的横截面为图示各种不同形状时，试问杆件会在哪个平面内失去稳定（即在失稳时，杆的截面绕哪一根轴转动）？解：(a),(b),(e)任意方向转动，(c),(d),(f)绕图示Z 轴转动。 15-2 图示各圆截面压杆，横截面积及材料都相同，直径d ＝1.6cm ，杆材A 3钢的弹性模量E =200MPa ，各杆长度及支承形式如图示，试求其中最大的与最小的临界力之值。解：(a) 柔度： 230 1500.4 λ?= = 相当长度：20.30.6l m μ=?= (b) 柔度： 150 1250.4 λ?== 相当长度：10.50.5l m μ=?= (c) 柔度： 0.770 122.50.4 λ?= = 相当长度：0.70.70.49l m μ=?= (d) 柔度： 0.590 112.50.4 λ?= = 相当长度：0.50.90.45l m μ=?= (e) 柔度： 145 112.50.4 λ?== 相当长度：10.450.45l m μ=?= 由E=200Gpa 及各柔度值看出：各压杆的临界力可用欧拉公式计算。即：() 22 cr EJ P l πμ=各压杆的EJ 均相同，故相当长度最大的压杆(a)临界力最小，压杆(d)与(e)的临界力最大，分别为： () 2948 2 2 2 320010 1.610640.617.6410cr EJ P l N π ππμ-??? ??= ==?

() 2948 2 2 2 320010 1.610640.4531.3010cr EJ P l N π ππμ-??? ??= ==? 15-3 某种钢材P σ=230MPa ，s σ=274MPa ，E =200GPa ，直线公式λσ22.1338-=cr ，试计算该材料压杆的P λ及S λ值，并绘制1500≤≤λ范围内的临界应力总图。解： 92.6 33827452.5 p s s a λπσλ===--=== 15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆，其外径和内径分别为，12mm 和10mm ，杆长为383mm ，两端为铰支座，材料的E ＝210GPa ，P σ=288MPa ，试求此挺杆的临界力cr P 。若实际作用于挺杆的最大压缩力P =2.33kN ，规定稳定安全系数W n =2~5。试校核此挺杆的稳定性。解：(1)

怎样推导压杆的临界力和临界应力公式.

06、基本知识怎样推导压杆的临界力和临界应力公式（供参考）同学们学习下面内容后，一定要向老师回信（849896803@https://www.360docs.net/doc/a88578821.html, ），说出你对本资料的看法（收获、不懂的地方、资料有错的地方），以便考核你的平时成绩和改进我的工作。回信请注明班级和学号的后面三位数。 1 * 问题的提出及其对策 (1) 1.1 问题的提出及其对策 ........................................................................................................ 1 1.2 压杆稳定分析概述——与强度、刚度分析对比 ............................................................ 2 2 压杆临界压力F cr 的计算公式 ................................................................................................. 3 2.1 压杆稳定的力学模型——弯曲平衡 ................................................................................ 3 2.2梁的平衡理论——梁的挠曲微分方程 ............................................................................. 4 2.3 按梁的平衡理论分析两端铰支的压杆临界压力 ............................................................ 6 2.4 按梁的平衡理论分析一端固定一端自由的压杆临界压力 ............................................ 8 2.5 按梁的平衡理论分析一端固定一端铰支的压杆临界压力 .......................................... 10 2.6 按梁的平衡理论分析两端固定的压杆临界压力 .......................................................... 14 2.7 将四种理想压杆模型的临界力公式及其推导分析图示的汇总 .. (18) 1 * 问题的提出及其对策 1.1 问题的提出及其对策试计算长度为400mm ，宽度为10mm ，厚度为1mm 的钢锯条，在一端固定、一端铰支的情况下，许用的轴向压力。材料的许用应力为160MPa 。解：1、按轴向拉压强度计计算 []2/160160120mm N MPa mm mm F A F N N ==≤?== σσ 2、按压杆稳定临界力公式计算 ()43 33 5120121121mm mm mm bh I Z =??== ()()N mm mm MPa l EI F CR 28.123 4002102000002 4 222=????==πμπ 分析：1、按轴向拉压杆的强度条件计算结果，该钢板尺可以安全承压 3.2kN 。这是一个什么概念呢？一袋水泥重50kg ，对应重力N s m kg mg W 500/10502 =?==，即该钢 kN N mm N mm mm F N 2.33200/1601202==??≤

材料力学的基本计算公式

材料力学的基本计算公式 Revised on November 25, 2020

材料力学的基本计算公式外力偶矩计算公式（P功率，n转速） 1.弯矩、剪力和荷载集度之间的关系式 2.轴向拉压杆横截面上正应力的计算公式（杆件横截面轴力F N，横截面面积A，拉应力为正） 3.轴向拉压杆斜截面上的正应力与切应力计算公式（夹角a 从x轴正方向逆时针转至外法线的方位角为正） 4.纵向变形和横向变形（拉伸前试样标距l，拉伸后试样标距l1；拉伸前试样直径d，拉伸后试样直径d1） 5.纵向线应变和横向线应变 6.泊松比 7.胡克定律

8.受多个力作用的杆件纵向变形计算公式 9.承受轴向分布力或变截面的杆件，纵向变形计算公式 10.轴向拉压杆的强度计算公式 11.许用应力，脆性材料，塑性材料 12.延伸率 13.截面收缩率 14.剪切胡克定律（切变模量G，切应变g ） 15.拉压弹性模量E、泊松比和切变模量G之间关系式 16.圆截面对圆心的极惯性矩（a）实心圆（b）空心圆 17.圆轴扭转时横截面上任一点切应力计算公式（扭矩T，所求点到圆心距离r）

18.圆截面周边各点处最大切应力计算公式 19.扭转截面系数，（a）实心圆（b）空心圆 20.薄壁圆管（壁厚δ≤ R0 /10 ，R0为圆管的平均半径）扭转切应力计算公式 21.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式 22.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同（如阶梯轴）时或 23.等直圆轴强度条件 24.塑性材料；脆性材料 25.扭转圆轴的刚度条件或 26.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,

(整理)压杆稳定计算.

第16 章压杆稳定 16.1 压杆稳定性的概念在第二章中，曾讨论过受压杆件的强度问题，并且认为只要压杆满足了强度条件，就能保证其正常工作。但是，实践与理论证明，这个结论仅对短粗的压杆才是正确的，对细长压杆不能应用上述结论，因为细长压杆丧失工作能力的原因，不是因为强度不够，而是由于出现了与强度问题截然不同的另一种破坏形式，这就是本章将要讨论的压杆稳定性问题。当短粗杆受压时（图16-1a），在压力F 由小逐渐增大的过程中，杆件始终保持原有的直线平衡形式，直到压力F 达到屈服强度载荷F s （或抗压强度载荷F b），杆件发生强度破坏时为止。但是，如果用相同的材料，做一根与图16-1a 所示的同样粗细而比较长的杆件（图16-1b），当压力F 比较小时，这一较长的杆件尚能保持直线的平衡形式，而当压力F 逐渐增大至某—数值F1时，杆件将突然变弯，不再保持原有的直线平衡形式，因而丧失了承载能力。我们把受压直杆突然变弯的现象，称为丧失稳定或失稳。此时，F1可能远小于F s （或F b）。可见，细长杆在尚未产生强度破坏时，就因失稳而破坏。图16－1 失稳现象并不限于压杆，例如狭长的矩形截面梁，在横向载荷作用下，会出现侧向弯曲和绕轴线的扭转（图16-2）；受外压作用的圆柱形薄壳，当外压过大时，其形状可能突然变成椭圆（图 16-3）；圆环形拱受径向均布压力时，也可能产生失稳（图16-4）。本章中，我们只研究受压杆件的稳定性。

所谓的稳定性是指杆件保持原有直线平衡形式的能力。实际上它是指平衡状态的稳定性。我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。第一种状态，小球在凹面内的 O 点处于平衡状态，如图 16-5a 所示。先用外加干扰力使其偏离原有的平衡位置，然后再把干扰力去掉，小球能回到原来的平衡位置。因此，小球原有的平衡状态是稳定平衡。第二种状态，小球在凸面上的 O 点处于平衡状态，如图 16-5c 所示。当用外加干扰力使其偏离原有的平衡位置后，小球将继续下滚，不再回到原来的平衡位置。因此，小球原有的干衡状态是不稳定平衡。第三种状态，小球在平面上的 O 点处于平衡状态，如图 16-5b 所示，当用外加干扰力使其偏离原有的平衡位置后，把干扰力去掉后，小球将在新的位置 O 1 再次处于平衡，既没有恢复原位的趋势，也没有继续偏离的趋势。因此。我们称小球原有的平衡状态为随遇平衡。图 16-5 图 16-6 通过上述分析可以认识到，为了判别原有平衡状态的稳定性，必须使研究对象偏离其原有的平衡位置。因此。在研究压杆稳定时，我们也用一微小横向干扰力使处于图 16-3

压杆稳定性计算

第16章压杆稳定压杆稳定性的概念在第二章中，曾讨论过受压杆件的强度问题，并且认为只要压杆满足了强度条件，就能保证其正常工作。但是，实践与理论证明，这个结论仅对短粗的压杆才是正确的，对细长压杆不能应用上述结论，因为细长压杆丧失工作能力的原因，不是因为强度不够，而是由于出现了与强度问题截然不同的另一种破坏形式，这就是本章将要讨论的压杆稳定性问题。当短粗杆受压时(图16-1a)，在压力F由小逐渐增大的过程中，杆件始终保持原有的直线平衡形式，直到压力F达到屈服强度载荷F s(或抗压强度载荷F b)，杆件发生强度破坏时为止。但是，如果用相同的材料，做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b)，当压力F比较小时，这一较长的杆件尚能保持直线的平衡形式，而当压力F逐渐增大至某—数值F1时，杆件将突然变弯，不再保持原有的直线平衡形式，因而丧失了承载能力。我们把受压直杆突然变弯的现象，称为丧失稳定或失稳。此时，F1可能远小于F s (或F b)。可见，细长杆在尚未产生强度破坏时，就因失稳而破坏。图16－1 失稳现象并不限于压杆，例如狭长的矩形截面梁，在横向载荷作用下，会出现侧向弯曲和绕轴线的扭转(图16-2)；受外压作用的圆柱形薄壳，当外压过大时，其形状可能突然变成椭圆(图16-3)；圆环形拱受径向均布压力时，也可能产生失稳(图16-4)。本章中，我们只研究受压杆件的稳定性。

力学计算公式

常用力学计算公式统计一、材料力学： 1.轴力（轴向拉压杆的强度条件） σ=N/A≤[σ]maxmax其中，N为轴力，A为截面面积 2.胡克定律（应力与应变的关系） σ=Eε或△L=NL/EA 其中σ为应力，E为材料的弹性模量，ε为轴向应变，EA为杆件的刚度（表示杆件抵抗拉、压弹性变形的能力） 3.剪应力（假定剪应力沿剪切面是均匀分布的） τ=Q/A Q其中，Q为剪力，A为剪切面面积Q4.静矩（是对一定的轴而言，同一图形对不同的坐标轴的静矩不同,如果参考轴通过图形的形心，则x=0，c y=0，此时静矩等于零）c对Z轴的静矩S=∫ydA=yA czA其中：S为静矩，A为图形面积，y 为形心到坐标轴的c3m。距离，单位为惯性矩5. 轴的惯性矩=∫dAy对Ay轴的距离，单位为y为形心到z为图2zI 形面积，A其中：常用简单图形的惯性矩33/12=bh/12，I=hbI矩形：yx4=πd/64 4m 圆形：I z44（πD1-a）/64，a=d/D=空心圆截面：I z（一）、求通过矩形形心的惯性矩 ∫Ay求矩形通过形心，的惯性矩I=x3h/2h/223 2dA

/3]/12=bh=[bybdy=IdydA=b·，则∫y（）-h/2-h/2x（二）、求过三角形一条边的惯性矩 /h·（h-y，dA=b·dy，b=bAyI=∫dA xxx32h2h dy yb/h）∫b（h-y）2） /h）dy=（yb –y=则I∫（0x03h4h3=bh=[by/3]-[by/4h]/1200 梁正应力强度条件（梁的强度通常由横截面上的正应 6.力控制）[/Wσ=M≤σ]zmaxmax为抗弯截面系数。M为弯矩，W其中：超静定问题及其解法7.根据静力学平衡1对一般超静定问题的解决办法是：（）、根据变形协调条件列出、2条件列出应有的平衡方程；（）根据力学与变形间的物理关系将变3（）、变形几何方程；形几何方程改写成所需的补充方程。抗弯截面模量8. W=I/y cxx其中I为对形心轴的惯性矩x9.抛物线形曲线的主要特性

压杆稳定

1、( )材料相同的压杆，柔度越大，稳定性越差，故它所能承受的外压力就越小。 1、( )压杆的临界应力是压杆处于临界状态维持直线平衡形式时横截面上的正应力。 2、( )材料相同，柔度相等的压杆，空心杆比实心杆的稳定性好，即空心杆所能承受的压力大。 3、对于压杆稳定，下面错误的伦述是( )。 A 、压杆的临界压力是保持稳定直线平衡的最大载荷。 B 、压杆的柔度越大，压杆越不稳定。 C 、大柔度压杆可以使用欧拉公式计算临界压力。 D 、矩形截面细长压杆，已知Iz>Ir ，计算临界载荷时，应取值Iz 为妥。 5、临界应力是压杆失稳时横截面上的应力（） 6、示Q235钢压杆，截面为矩形，面积为3.2*103mm 2，已知E=200GPA ，σs =235MPA ，λp=100,λs=61.6，试计算其临界载荷。（15分） 7、( )压杆的稳定性主要与压杆的截面大小和压杆的长度有关。一、是非判断题 9.1 所有受力构件都存在失稳的可能性。（ × ） 9.2 在临界载荷作用下，压杆既可以在直线状态保持平衡，也可以在微弯状态下保持平衡。（ × ） 9.3 引起压杆失稳的主要原因是外界的干扰力。（ × ） 9.4 所有两端受集中轴向力作用的压杆都可以采用欧拉公式计算其临界压力。（ × ） 9.5 两根压杆，只要其材料和柔度都相同，则他们的临界力和临界应力也相同。（ × ） 9.6 临界压力是压杆丧失稳定平衡时的最小压力值。（ ∨ ） 9.7 用同一材料制成的压杆，其柔度（长细比）愈大，就愈容易失稳。（ ∨ ） 9.8 只有在压杆横截面上的工作应力不超过材料比例极限的前提下，才能用欧拉公式计算其临界压力。（ × ） 9.9 满足强度条件的压杆不一定满足稳定性条件；满足稳定性条件的压杆也不一定满足强度条件。（ ∨ ） 9.10 低碳钢经过冷作硬化能提高其屈服极限，因而用同样的方法也可以提高用低碳钢制成的细长压杆的临界压力。（ × ）二、填空题 9.1 压杆的柔度λ综合地反映了压杆的对临界应力的影响。长度(l )，约束(μ)，横截面的形状和大小（i ）有应力集中时

杆件的内力计算

第三章　杆件的内力计算内力的大小及其分布规律与杆件的变形与失效密切相关，因此内力分析是解决构件承载能力的基础。本章主要研究杆件的内力及其沿杆件轴线的变化规律，以便为杆件的强度、刚度和稳定性计算提供基础。内容提要一、内力与截面法１畅内力的概念作用于杆件上的载荷和支座约束力称为外力。由外力引起的杆件内部作用力的改变量，称为附加内力，简称为内力。机械工程力学主要研究受力杆件横截面上的内力。根据连续性假设可知，内力在横截面上是连续分布的，组成一分布内力系，通常所说的内力是指该分布内力系的简化结果。２畅截面法将杆件假想地截开以显示内力，并由平衡方程确定内力的方法，称为截面法，它是计算杆件内力的基本方法，其步骤可归结为：（１）截———沿欲求内力的截面假想地将杆件截为两部分；（２）取———任取其中一部分为研究对象；（３）代———用欲求的内力代替另一部分对研究对象的作用；（４）平———列出研究对象的平衡方程，确定内力的大小和方向。应用截面法时应注意：（１）截面不能取在集中力或集中力偶的作用面上；（２）未知的内力均设为正。二、轴向拉压杆的内力与内力图１畅轴向拉压杆件的受力与变形特征杆件是直杆，作用于杆件上的外力合力作用线与杆件轴线重合，杆件变形是沿轴线方向的伸长或缩短。这种变形形式称为轴向拉伸或轴向压缩，这类杆件称为拉杆或压杆。２畅拉压杆横截面上的内力———轴力杆件轴向拉伸或压缩时，横截面上的内力与轴线重合，这种与杆件轴线重合的内力称为轴力，用FＮ表示。使杆件受拉伸时的轴力为正，此时轴力背离截面，称为拉力；使杆件受压缩时的轴力为负，此时轴力指向截面，称为压力。 ·45·

材料力学的基本计算公式

材料力学的基本计算公式外力偶矩计算公式（P功率，n转速） 1.弯矩、剪力和荷载集度之间的关系式 2.轴向拉压杆横截面上正应力的计算公式（杆件横截面轴力F N，横截面面积A，拉应力为正） 3.轴向拉压杆斜截面上的正应力与切应力计算公式（夹角 a 从x轴正方向逆时针转至外法线的方位角为正） 4.纵向变形和横向变形（拉伸前试样标距l，拉伸后试样标距l1；拉伸前试样直径d，拉伸后试样直径d1） 5.纵向线应变和横向线应变 6.泊松比

8.圆轴扭转时横截面上任一点切应力计算公式（扭矩T，所求点到圆心距离r） 9.圆截面周边各点处最大切应力计算公式 10.扭转截面系数，（a）实心圆（b）空心圆 11.薄壁圆管（壁厚δ≤ R0/10 ，R0为圆管的平均半径）扭转切应力计算公式 12.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式 13.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同（如阶梯轴）时或 14.等直圆轴强度条件 15.塑性材料；脆性材料 16.扭转圆轴的刚度条件? 或 17.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,

18.平面应力状态下斜截面应力的一般公式 , 19.平面应力状态的三个主应力 , , 20.主平面方位的计算公式 21.面内最大切应力 22.受扭圆轴表面某点的三个主应力，， 23.三向应力状态最大与最小正应力 , 24.三向应力状态最大切应力 25.广义胡克定律

26.四种强度理论的相当应力 27.一种常见的应力状态的强度条件， 28.组合图形的形心坐标计算公式， 29.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式 30.截面图形对轴z和轴y的惯性半径? , 31.平行移轴公式（形心轴z c与平行轴z1的距离为a，图形面积为A） 32.纯弯曲梁的正应力计算公式 33.横力弯曲最大正应力计算公式

压杆稳定性计算

第16章压杆稳定 16、1 压杆稳定性的概念在第二章中,曾讨论过受压杆件的强度问题,并且认为只要压杆满足了强度条件,就能保证其正常工作。但就是,实践与理论证明,这个结论仅对短粗的压杆才就是正确的,对细长压杆不能应用上述结论,因为细长压杆丧失工作能力的原因,不就是因为强度不够,而就是由于出现了与强度问题截然不同的另一种破坏形式,这就就是本章将要讨论的压杆稳定性问题。当短粗杆受压时(图16-1a),在压力F由小逐渐增大的过程中,杆件始终保持原有的直线平衡形式,直到压力F达到屈服强度载荷F s(或抗压强度载荷F b),杆件发生强度破坏时为止。但就是,如果用相同的材料,做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b),当压力F比较小时,这一较长的杆件尚能保持直线的平衡形式,而当压力F逐渐增大至某—数值F1时,杆件将突然变弯,不再保持原有的直线平衡形式,因而丧失了承载能力。我们把受压直杆突然变弯的现象,称为丧失稳定或失稳。此时,F1可能远小于F s (或F b)。可见,细长杆在尚未产生强度破坏时,就因失稳而破坏。图16－1 失稳现象并不限于压杆,例如狭长的矩形截面梁,在横向载荷作用下,会出现侧向弯曲与绕轴线的扭转(图16-2);受外压作用的圆柱形薄壳,当外压过大时,其形状可能突然变成椭圆(图16-3);圆环形拱受径向均布压力时,也可能产生失稳(图16-4)。本章中,我们只研究受压杆件的稳定性。

图16-3 所谓的稳定性就是指杆件保持原有直线平衡形式的能力。实际上它就是指平衡状态的稳定性。我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。第一种状态,小球在凹面内的O点处于平衡状态,如图16-5a所示。先用外加干扰力使其偏离原有的平衡位置,然后再把干扰力去掉,小球能回到原来的平衡位置。因此,小球原有的平衡状态就是稳定平衡。第二种状态,小球在凸面上的O点处于平衡状态,如图16-5c所示。当用外加干扰力使其偏离原有的平衡位置后,小球将继续下滚,不再回到原来的平衡位置。因此,小球原有的干衡状态就是不稳定平衡。第三种状态,小球在平面上的O点处于平衡状态,如图16-5b所示,当用外加干扰力使其偏离原有的平衡位置后,把干扰力去掉后,小球将在新的位置O1再次处于平衡,既没有恢复原位的趋势,也没有继续偏离的趋势。因此。我们称小球原有的平衡状态为随遇平衡。图16-5 图16-6 通过上述分析可以认识到,为了判别原有平衡状态的稳定性,必须使研究对象偏离其原有的平衡位置。因此。在研究压杆稳定时,我们也用一微小横向干扰力使处于直线平衡状态的压杆偏离原有的位置,如图16-6a所示。当轴向压力F 由小变大的过程中,可以观察到: 1)当压力值F1较小时,给其一横向干扰力,杆件偏离原来的平衡位置。若去掉横向干扰力后,压杆将在直线平衡位置左右摆动,最终将恢复到原来的直线平衡位置,如图16-6b所示。所以,该杆原有直线平衡状态就是稳定平衡。 2)当压力值F2超过其一限度F cr时,平衡状态的性质发生了质变。这时,只要有一轻微的横向干扰,压杆就会继续弯曲,不再恢复原状,如图16-6d所示。因此,该杆原有直线平衡状态就是不稳定平衡。