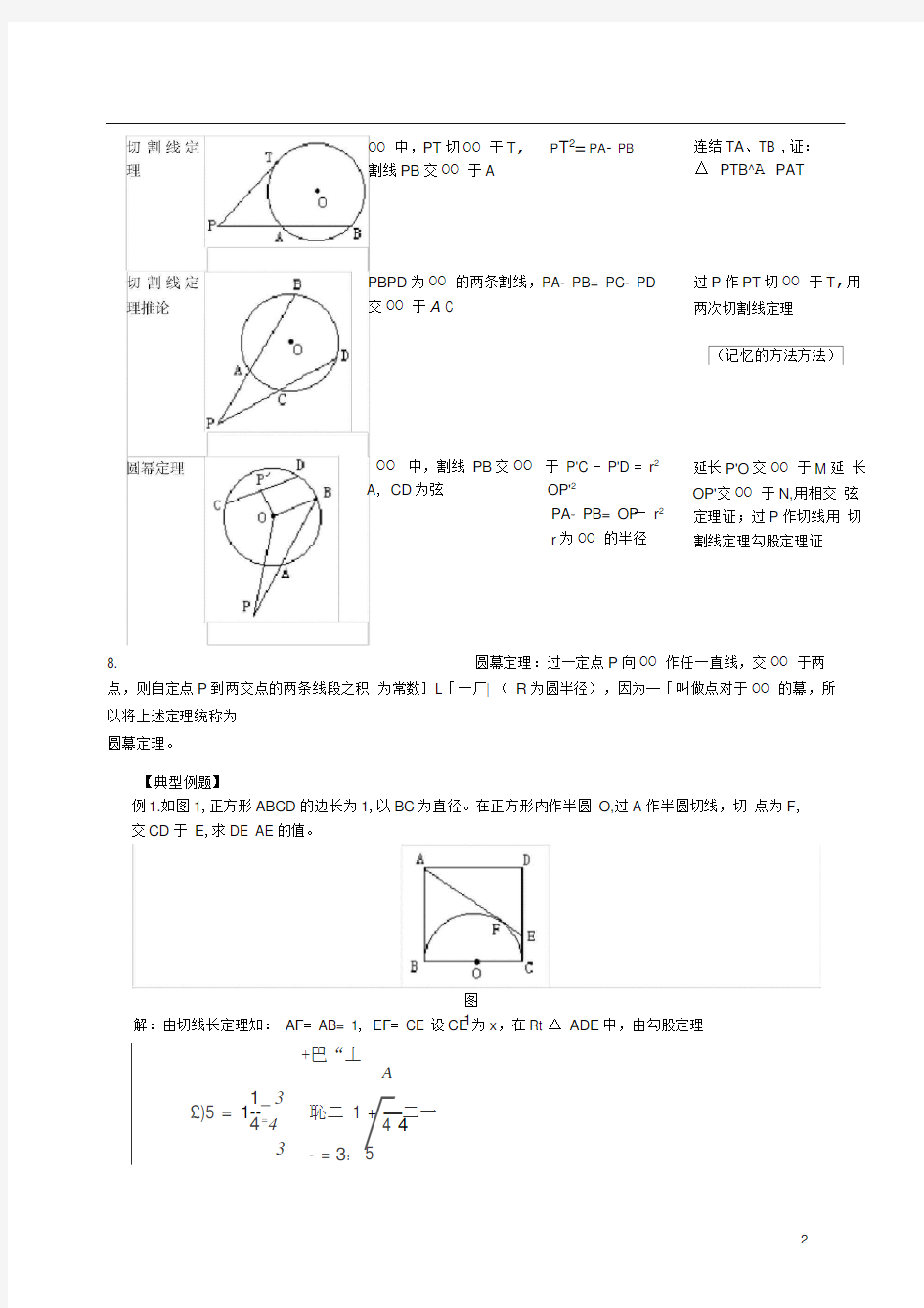
(完整版)切线长定理、弦切角定理、切割线定理、相交弦定理

相交弦定 C
OO 中,AB 为直径,CDLABPC = PA- PB.
理的推论
/
于P.
|(特殊情况)|
127
用相交弦定理
切线长定理、弦切角定理、切割线定理、相交弦定理
以及与圆有关的比例线段
[学习目标] 1. 切线长概念
切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线 上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。 (PA 长)
2. 切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等; (2)若已知两条切
线平行,则圆上两个切点的连线为直径;
(3)经过圆外一点引圆的两条切线,连结两个切点可得
4.弦切角定理: 弦切角等于其所夹的弧所对的圆周角。
5. 弄清和圆有关的角: 圆周角,圆心角,弦切角,圆内角,圆外角。
6. 遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定
7. 与圆有关的比例线段 定理 已知
结论
证法
OO 中,AB CD 为弦,交 PA- PB= PC- PD. 连 结 AC 、 BD ,证: 于 P.
△ APCo A DPB.
到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角 互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
直线AB 切OO 于P , PC PD 为弦,图中几个弦切角呢?(四个)
相交弦定
8. 圆幕定理:过一定点P向OO作任一直线,交OO于两
点,则自定点P到两交点的两条线段之积为常数]L「一厂| (R为圆半径),因为--「叫做点对于OO的幕,所
以将上述定理统称为
圆幕定理。
解:由切线长定理知:AF= AB= 1, EF= CE 设CE为x,在Rt △ ADE中,由勾股定理
+巴“丄
A
1_3「
£)5 = 1--恥二1 + —二一
4=4 4 4
3- = 3
:
5
P T2=PA- PB
PBPD为OO的两条割线,PA- PB= PC- PD
交OO于A C
OO 中,割线PB交OO 于P'C - P'D = r2
A, CD为弦OP'2
PA- PB= OP—r2
r为OO的半径
连结TA、TB ,证:
△PTB^A PAT
过P作PT切OO于T,用
两次切割线定理
(记忆的方法方法)
延长P'O交OO于M延长
OP'交OO于N,用相交弦
定理证;过P作切线用切
割线定理勾股定理证
OO中,PT切OO于T,
割线PB交OO于A
【典型例题】
例1.如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O,过A作半圆切线,切点为F,
交CD于E,求DE AE的值。
图
1
44
例2. OO中的两条弦AB与CD相交于E,若AE= 6cm, BE= 2cm, CD= 7cm 那么CE=
cm。Array解:由相交弦定理,得
AE- BE= CE- DE
■/ AE= 6cm, BE= 2cm, CD= 7cm,
DE=CD-CE =1-CE
.6冥2=強(7?6)
… ,
即亡费+12 = 0
/? CE= 3cm或CE= 4cm。
故应填3或4。
点拨:相交弦定理是较重要定理,结果要注意两种情况的取舍。
例3.已知PA是圆的切线,PCB是圆的割线,则*小:AC2 = $氏
解:???/ P=ZP
/ PAC=Z B,
???△PAC^A PBA
AB _ PB
...疋二7Z,
又??? PA是圆的切线,PCB是圆的割线,由切割线定理,得
M 二刃,FC
AB2_ 阳_ FS
? ^^ _ 円■花-丽
… ,
即乂炉:Q=PC
故应填PCo
点拨:利用相似得出比例关系式后要注意变形,推出所需结论。
例4.如图3, P是OO外一点,PC切OO于点C, PAB是OO的割线,交OO于A B两点,如果PA: PB= 1 : 4, PC= 12cm OO的半径为10cm 则圆心o到AB的距离是_______________ cm。
解:?/ PC是OO的切线,PAB是OO的割线,且PA: PB= 1 : 4
??? PB= 4PA
又??? PC= 12cm
由切割线定理,得?,-': _
...1一
???二一二:
?PB= 4X 6= 24 (cm)
?AB= 24 —6 = 18 (cm)
设圆心O到AB距离为d cm,
由勾股定理,得
故应填J」。
例5.如图4, AB为OO的直径,过B点作OO的切线BC, OC交OO于点E, AE的延长线交BC于点D,( 1)求证:占—JU ; (2)若AB= BC= 2厘米,求CE CD的长。
证明:(1)连结BE
ED是?0的切线=>Z J4=Z.CBE
OA = OB = Z^= Z10EA 乙
QEA =S EC
FF CB
点悟:要证
HUEDS心EE=> ——=——=> 窗=CB * CD
CD CS
?=> 丄ABD = 90° -
血二2 n O 吕二1 U g = 用门
胆是0沏线 应为直径 (2)
BC = 2
OS = A
又-'-
??? 厘米。
点拨:有切线,并需寻找角的关系时常添辅助线,为利用弦切角定理创造条件。
例6.如图5,AB 为OO 的直径,弦
证明:连结BD, ?/AE 切OO 于 A
???/ EAD=Z ABD
?/ AE! AB 又 AB// CD ? AE! CD
? AB 为OO 的直径
???/ ADB= 90° ???/ E =Z ADB= 90° ? △ AD 0A
BAD
AD DE
药二75 AD 2
= AB* DE
? CD// AB
c n
AD= BC
? AD= BC,
EC 2 = AS* DS
E 。
点悟:由结论
AD- BC= CD- AB 得… --,显然要证厶PAB A PBA 和厶PC SA PBC
证明:?/ PA 切OO 于A ,
???/ PAD=Z PBA 又/ APD=Z BPA ? △ PAD^A PBA £ 旳
.? . I :-: J '
同理可证厶PCD^A PBC
CD PD
? _ / 一一
?/ PA PC 分别切OO 于A 、C ? PA= PC
M
CD
,
=1^p
」
,
? .l< 『I
? AD- BC= DC- AB 求证:BC = 2OE
点悟:由要证结论易想到应证 。丘是厶ABC 的中位线。而 OA= OB 只须证AE = CE, 证明:连结OD ?/ ACL AB AB 为直径
? AC 为OO 的切线,又 DE 切OO 于D ? EA= ED, ODL DE ?/ OB= OD ?/ B =Z ODB 在 Rt △ ABC 中,/ C = 90°—/B
???/ ODE= 90° 厶DO9IT - £ODB ? / C =Z EDC
? ED= EC ? AE = EC
例7.如图6, PA PC 切OO 于A 、C ,
CD- AB
例8.如图7,在直角三角形 ABC 中,/ A = 90°,以 AB 边为直径作O O,交斜边 BC 于点D,过D 点 作OO 的切线交AC 于 E 。
图7
