小学奥数勾股定理与弦图讲解

第十二讲勾股定理与弦图
【教学重难点】
能够用弦图证明勾股定理的具体内容,并运用勾股定理解决相应的几何问题。【教学内容】
勾股定理是一个基本的几何定理。直角三角形两直角边(即
“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2o
勾股定理
第一部分:勾股定理的应用
H
介绍一种神奇的无字证明
b
10
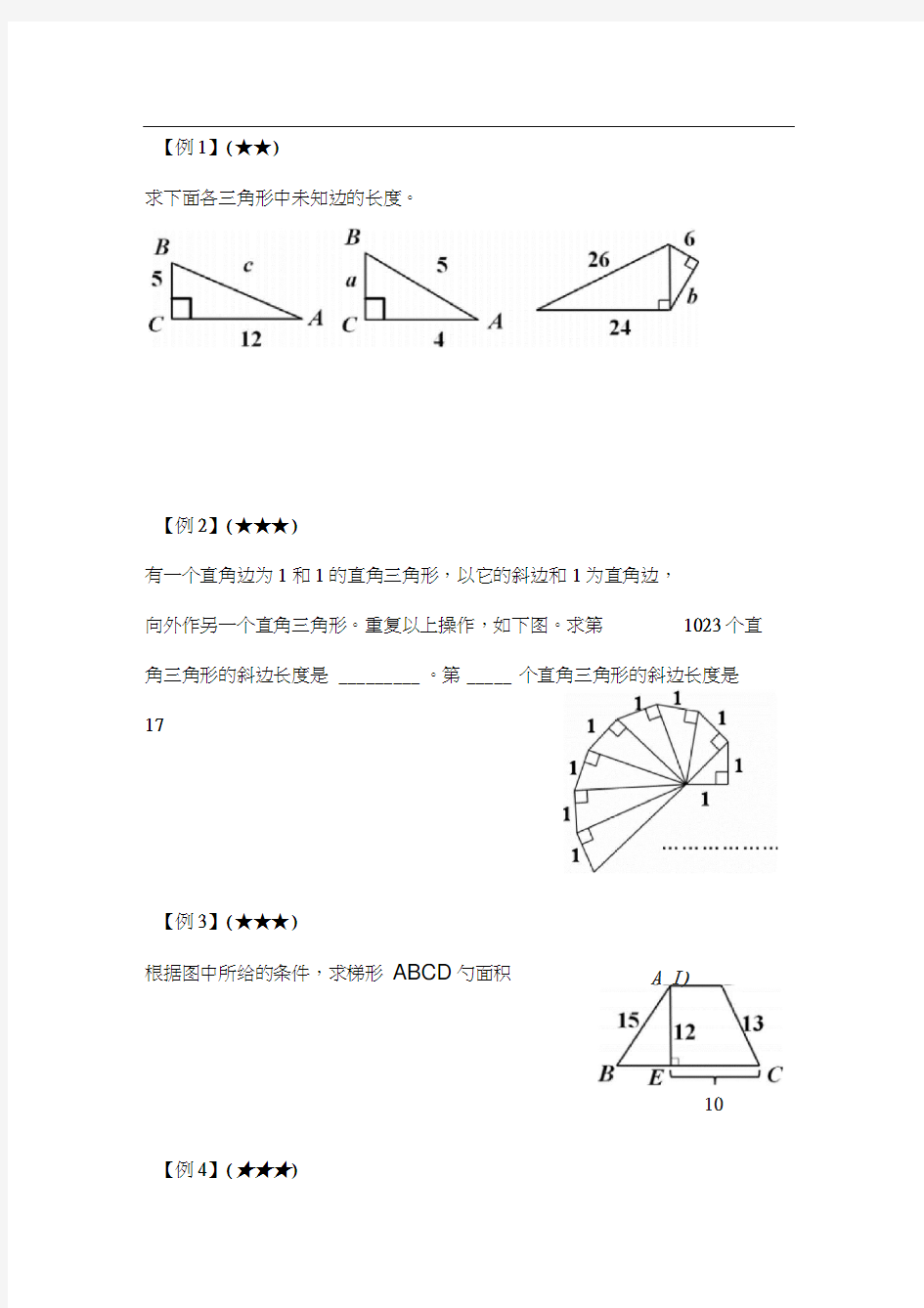
【例1】(★★)
求下面各三角形中未知边的长度。
【例2】(★★★)
有一个直角边为1和1的直角三角形,以它的斜边和1为直角边,
向外作另一个直角三角形。重复以上操作,如下图。求第 1023个直 角三角形的斜边长度是 _________ 。第 _____ 个直角三角形的斜边长度是 17
【例3】(★★★)
根据图中所给的条件,求梯形 ABCD 勺面积 【例4】(★★★)
A I)
【例5】(★★★★)
第二部分:介绍弦图及其应用
⑴大正方形边长为:a + b
⑵小正方形边长为:a — b
⑶中正方形边长为:
c
【例6】(★★★)
一个直角三角形的斜边长8厘米,两个直角边的长度差为 2厘
如图,请根据所给的条件,计算出大梯形的面积(单位:厘米) 如图,在四边形 ABCD 中,AB= 30 ,AD= 48, BC= 14 , CD= 40,/
ADBk Z DB G 90°。请问:四边形 ABCD 的面积是多少?
O
B
(基本思想是图形经过割补后,面积不变)
【例7 ] ( ★★★★★)
从一块正方形玻璃上裁下宽为16分米的一长方形条后,剩下的那块
长方形的面积为336平方分米,原来正方形的面积是多少平方分米?
自我检测
1.将长为10米的梯子斜靠在墙上,若梯子上端到墙的底端距离为6
米,则梯足到墙的底端距离为 _______________ .
2.若直角三角形一直角边和斜边分别为17和145,则另一直角边
为_____________ 。
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方
米,求这个三角形的面积?
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为
_____________ c m.
5.如图在△ ABC中,AB =15,AC=13,高AD=12则厶ABC勺面积为?
易错题
(1)某人以匀速行走在一条公路上,公路两端的车站每隔相同的时间开出一
辆公共汽车,该行人发现每隔30分钟就会有一辆公共汽车追上他;而每隔20分钟有一辆公共汽车迎面开来.问车站每隔多少分钟开出一辆车?
(2)有4袋糖块,其中任意3袋的总块数都超过90。这4袋糖块总
共最少有多少块?
(3)—次考试共30道题。若佳佳,海海,阳阳和娜娜分别答对26, 27, 28, 29道。则四人都答对的题目至少多少道?(先最再对:先从最值的方向分析,最后检验是否正确)
勾股定理与弦图练习题
勾股定理与弦图练习题 选择题(12×3′=36′) 1.已知一个Rt△的两边长分别为3和4,则第三边长的平方是() A、25 B、14 C、7 D、7或25 2.下列各组数中,以a,b,c为边的三角形不是Rt△的是() A、a=1.5,b=2,c=3 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=5 3.若线段a,b,c组成Rt△,则它们的比为() A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7 4.Rt△一直角边的长为11,另两边为自然数,则Rt△的周长为() A、121 B、120 C、132 D、不能确定 5.如果Rt△两直角边的比为5∶12,则斜边上的高与斜边的比为() A、60∶13 B、5∶12 C、12∶13 D、60∶169 6.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是() A、2n B、n+1 C、n2-1 D、n2+1 7.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是() A、24cm2 B、36cm2 C、48cm2 D、60cm2 8.等腰三角形底边上的高为8,周长为32,则三角形的面积为() A、56 B、48 C、40 D、32 9.三角形的三边长为(a+b)2=c2+2ab,则这个三角形是( ) A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要() A、450a元 B、225a 元 C、150a元 D、300a元 1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为() A、6cm2 B、8cm2 C、10cm2 D、2cm2 2.已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( ) A、25海里 B、30海里 C、35海里 D、40海里 1.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△A BC=________。 2.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。 3.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是________m。
第84讲、勾股定理与弦图---加深版
第84讲、勾股定理与弦图 -----加深版 一、基础知识; 我国是最早了解勾股定理的国家之一,在直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。 二、图形的构造定理; 1、勾股定理: 在直角三角形中,两条直角边的平方和等于斜边的平方和。 a c 2 2 2c b a= + b 2、勾理的证明:大家注意到,每个长方形可用一条对角线分为两个同样大小的直角三角形,如下图。设这个直角三角形的两条直角边为a,b,斜边为c,则4个直角三角形可以拼成一个斜边为c的正方形。中间空一格边长为a-b的小正方形。显然这个图形是大正方形ABCD的一部分。由图中可见。 证明:ab b a c 2 4 ) (? + - = ab b a2 ) (2+ - = ab b ab a2 22 2+ + - = =a2-2ab+b2+2ab =a2+b2 完全平方和公式: 完全平方差公式:
1. 四个完全一样的长方形木板,拼成如图的正方形,大正方形周长32厘米,小正方 形周长24厘米。求:每块长方形木板的面积和周长。 2. 如图,在△ABD 中,∠A 是直角,AB =3,AD =4,BC =12,DC =13,求四边形 ABCD 的面积 3、以直角三角形ABC 各边为直径的三个半圆围成两个新月形(阴影部分),已知AC 长3厘米,长4米.则新月形(阴影部分)的面积和是多少平方厘米。
4、同样大小的长方形小纸片摆成了下图所示的图形,已知小纸片的宽是12厘米,求阴影部分的总面积。 1、所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A ,B ,C ,D 的面积之和为 cm2. 2、如下图所示,小圆直径与大圆直径在同一条直线上,弦AB=10厘米,弦AB 与直径平行且与小圆相切,求阴影面积。
勾股定理及弦图题库
勾股定理及弦图题库Last revision on 21 December 2020
勾股定理及弦图题库 这就是一个“弦图”。“弦”图是由八个完全一样的直角三角形拼成四个相同的长方形围成的,中间空出一个小正方形。 三国时期的吴国数学家赵爽,就利用这“弦图”对勾股定理作出了严格而简捷的证明。我们也可以根据“弦图”中大小正方形与长方形的关系,得到一些面积问题的解题思路。 【例】.2002年在北京召开了国际数学家大会,大会会标如下图所示,它由四个相同的直角三角形拼成的(直角边的长度分别为2和3),问大正方形的面积是多少 【例】在边长为10的正方形ABCD中,内接着6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这6个小正方形的总面积是。 【例】.如图,如果长方形ABCD的面积是56cm2,那么四边形MNPQ的面积是多少cm2 【例】点P是正方形ABCD外一点,PB=12cm,APB的面积是90cm2,CPB的面积是48cm2。请你回答:正方形 ABCD的面积是多少cm2 【例】如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则矩形ABCD的面积为
【例】如下图,正方形ABCD的面积是S,A、B、C、D分别是线段EB、FA、GD、HC的三等分点,试用S表示四边形EFGH的面积S1; 【例】(2009安顺)下图是我国古代着名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是—— 【例】( 2010年广西河池)如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边( x>y),下列四个说法:① x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是().A.①② B.①②③ C.①②④ D.①②③④ 【例】( 2011年浙江温州)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图” ,后人称其为“赵爽弦图” .图7由“弦图” 变化得到的,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=10,则S2的值是______【例】小明遇到这样一个问题:如图13,在边长为a ( a>2)的正方形 ABCD 各边上分别截取 AE =BF =CG =DH =1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形.请回答: ( 1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),求这个新的正方形的边长; ( 2)求正方形MNPQ的面积.
勾股定理及弦图题库
勾股定理及弦图题库 这就是一个“弦图”。“弦”图是由八个完全一样的直角三角形拼成四个相同的长方形围成的,中间空出一个小正方形。 三国时期的吴国数学家赵爽,就利用这“弦图”对勾股定理作出了严格而简捷的证明。 我们也可以根据“弦图”中大小正方形与长方形的关系,得到一些面积问题的解题思路。 【例】.20XX年在北京召开了国际数学家大会,大会会标如下图所示,它由四个相同的直角三角形拼成的(直角边的长度分别为2和3),问大正方形的面积是 多少? 【例】在边长为10的正方形ABCD中,内接着6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这6个小正方形的总面积是。 【例】.如图,如果长方形ABCD的面积是56cm2,那么四边形MNPQ 的面积是多少cm2? 【例】点P是正方形ABCD外一点,PB=12cm,?APB的面积是90cm2, ?CPB的面积是48cm2。请你回答:正方形ABCD的面积是多少 cm2?
【例】如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶 点,若四边形EFGH的面积为1,则矩形ABCD 的面积为 【例】如下图,正方形ABCD的面积是S,A、B、C、 D分别是线段EB、FA、GD、HC的三等分点,试用S ; 表示四边形EFGH的面积S 1 【例】(2009?安顺)下图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是——
五年级奥数.几何.勾股定理与弦图(B级)学生版
MSDC 模块化分级讲义体系 五年级奥数. 几何.勾股定理与弦图(B 级).学生版 Page 1 of 16 华盛顿的傍晚 亲爱的小朋友们: “在那山的那边海那边的美国首都华盛顿,有一位中年人,他聪明又勤奋,他潜心探讨,他反复思考与演算……”那是1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德 便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 具体方法如下: 两个全等的Rt △ABC 和Rt △BDE 可以拼成直角梯形ACDE , 则梯形面积等于三个直角三角形面积之和。即 (AC +DE )×CD÷2=AC×BC÷2+BD×DE÷2+AB×BE÷2 (a +b )2÷2=a×b÷2+a×b÷2+c×c÷2 化简整理得a 2+b 2=c 2 课前预习 勾股定理与弦图
勾股定理与弦图练习(含答案)
勾股定理与弦图练习(含答案) 判断题 ⑴在一个三角形中,如果一边上的中线等于这条边的一半,那么这条边所对的角是直角. ⑵命题:“在一个三角形中,有一个角是30°,那么它所对的边是另一边的一半.”的逆命题是真命题. ⑶勾股定理的逆定理是:如果两条直角边的平方和等于斜边的平方,那么这个三角形是直角三角形. ⑷△ABC的三边之比是1:1:,则△ABC是直角三角形. 答案:对,错,错,对; △ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是() A.如果∠C-∠B=∠A,则△ABC是直角三角形. B.如果c2=b2—a2,则△ABC是直角三角形,且∠C=90°. C.如果(c+a)(c-a)=b2,则△ABC是直角三角形. D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形. 答案:D 1、下列四条线段不能组成直角三角形的是() A.a=8,b=15,c=17 B.a=9,b=12,c=15 C.a= ,b= ,c= D.a:b:c= 2:3:4 答案:D 2、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?
⑴a= ,b= ,c= ;⑵a=5,b=7,c=9; ⑶a=2,b= ,c= ;⑷a=5,b= ,c=1. 答案:⑴是,∠B;⑵不是;⑶是,∠C;⑷是,∠A. 叙述下列命题的逆命题,并判断逆命题是否正确. ⑴如果a3>0,那么a2>0; ⑵如果三角形有一个角小于90°,那么这个三角形是锐角三角形; ⑶如果两个三角形全等,那么它们的对应角相等; ⑷关于某条直线对称的两条线段一定相等. 答案:⑴如果a2>0,那么a3>0;假命题. ⑵如果三角形是锐角三角形,那么有一个角是锐角;真命题. ⑶如果两个三角形的对应角相等,那么这两个三角形全等;假命题. ⑷两条相等的线段一定关于某条直线对称;假命题. 1、填空题. ⑴任何一个命题都有,但任何一个定理未必都有. ⑵“两直线平行,内错角相等.”的逆定理是. ⑶在△ABC中,若a2=b2-c2,则△ABC是三角形,是直角;若a2<b2-c2,则∠B是. ⑷若在△ABC中,a=m2-n2,b=2mn,c=m2+n2,则△ABC是三角形. 答案:⑴逆命题,逆定理;⑵内错角相等,两直线平行;⑶直角,∠B,钝角;⑷直角.
小学奥数勾股定理
勾股定理 内容概述 1.勾股定理(毕达哥拉斯定理):直角三角形中的两直角边平方后的和等于斜边的平方. 公元前500年古希腊的毕达哥拉斯发现了勾股定理后,曾宰牛百头,广设盛筵以示庆贺. 2. 公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘.得成三、四、五. 三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实. 汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句,长面曰股,相与结角曰弦.句短其股,股短其弦. 句股各自乘,并,而开方除之,即弦. 中国科学院数学与系统科学研究院的徽标(右图所示)采用的就是赵爽 的弦图.2002年在北京举行的国际数学家大会的徽标也是弦图. 如下,在弦图中有EFGH S = 四边形()12ABCD MNPQ S S +矩形矩形C DG ADG CDE S S S '==
3. 伽菲尔德证法:美国第20任总统伽菲尔德对数学有浓厚的兴趣,在还是中学教师时曾给出一种勾股定理的证明方法: 梯形面积=12(上底+下底)×高 =12(a+b)×(a +b) =12 (a+b )2; 三个直角三角形的面积和=12ab+12ab +12 c 2; 梯形面积=三个直角三角形面积和. 12(a +b)2=12ab+12ab+12 c 2,所以a 2+b2=c 2. 4. 公元前3世纪的欧几里得在《几何原本》中给出一种证明,简叙如下: 如图,作出三个正方形,它们的边长分别为直角三角形ABC 的三边长.连接图中的虚线段对应的点;过C作C K平行于AF,交AB、FG 分别于J 、K 点. 易证△AFC ≌△BAE,有12FAC S =AF.FK=12AFKJ S 矩形,12 BAE S =EA .CA=ACDE S 正方形,所以AFKJ S =矩形 ACDE S 正方形; 易证△CBG≌△HBA,有12CBG S =BG.KG=12KGBJ S 矩形,12 HBA S =BH.IH =CBHI S 正方形,所以KGBJ S 矩形 CBHI S =正方形. 而AFGB AFKJ S S =正方形矩形KGBJ ACBE S S +=矩形正方形CBHI S +正方形. 即有A B2=AC 2+CB 2 .
五年级奥数.几何.勾股定理与弦图(C级).学生版
华盛顿的傍晚 亲爱的小朋友们: “在那山的那边海的那边的美国首都华盛顿,有一位中年人,他聪明又勤奋,他潜心探讨,他反复思考与演算……”,那是1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 具体方法如下: 两个全等的 Rt △ ABC 和Rt △BDE 可以拼成直角梯形ACDE , 则梯形面积等于三个直角三角形面积之和。即 (AC +DE )×CD÷2=AC×BC÷2+BD×DE÷2+AB×BE÷2 (a +b )2÷2=a×b÷2+a×b÷2+c×c÷2 化简整理得a 2+b 2=c 2 课前预习 勾股定理与弦图
点评:此种解法主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2. 而在我国对于勾股定理的证明又做出了那些贡献哪? 在我国古代,把直角三角形叫做勾股形。把直角三角形的较短直角边称为“勾”,较长直角边为“股”,斜边称为“弦”,所以把这个定理称为“勾股定理”。勾股定理揭示了直角三角形边之间的关系。即:在直角三角形中俩条直角边的平方和等于斜边的平方。公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘.得成三、四、五. 三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实. 汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句,长面曰股,相与结角曰弦.句短其股,股短其弦. 句股各自乘,并,而开方除之,即弦。 勾股定理的证明:
小学奥数勾股定理与弦图讲解
小学奥数勾股定理与弦 图讲解 Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998
的面积。 如图,请根据所给的条件,计算出大梯形的面积(单位:厘米)。
如图,在四边形ABCD 中,AB=30 ,AD=48,BC=14 ,CD=40,∠ADB+∠DBC=90°。请问:四边形ABCD 的面积是多少 第二部分:介绍弦图及其应用 (基本思想是图形经过割补后,面积不变) ⑴大正方形边长为:a+b ⑵小正方形边长为:a-b ⑶中正方形边长为:c 【例 6】(★★★) 一个直角三角形的斜边长 8 厘米,两个直角边的长度差为2 厘米,求这个三角形的面积 【例 7】(★★★★★) 从一块正方形玻璃上裁下宽为16 分米的一长方形条后,剩下的那块长方形的面积为336 平方分米,原来正方形的面积是多少平方分米 自我检测 1.将长为10 米的梯子斜靠在墙上,若梯子上端到墙的底端距离为 6 米,则梯足到墙的底端距离为__________米. 2.若直角三角形一直角边和斜边分别为17 和145 ,则另一直角边 为___________。 3.已知一个直角三角形的两边长分别为3 和4,则第三边长的平方 是。
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为___________cm2. 5.如图在△ABC中,AB =15,AC=13,高AD=12,则△ABC的面积为 易错题 (1)某人以匀速行走在一条公路上,公路两端的车站每隔相同的时间开出一辆公共汽车,该行人发现每隔30分钟就会有一辆公共汽车追上他;而每隔20分钟有一辆公共汽车迎面开来.问车站每隔多少分钟开出一辆车 (2)有4袋糖块,其中任意3袋的总块数都超过90。这4袋糖块总共最少有多少块 (3)一次考试共30道题。若佳佳,海海,阳阳和娜娜分别答对26,27,28,29道。则四人都答对的题目至少多少道(先最再对:先从最值的方向分析,最后检验是否正确)
小学奥数华杯赛几何之勾股定理与弦图
小学奥数华杯赛几何之勾股定理与弦图 关于勾股定理,我们已经谈过很多了。中国、希腊、埃及这些文 明古国,处于不同的地区,不过却都很早地,独立地发现了勾股定理。那么,勾股定理到底是谁ZUI先发现的呢?我们能够自豪地说:是我们 中国人ZUI先发现的。证据就是《周髀算经》中的记载。 《周髀算经》一开始,就记载了我国周朝初年的大政治家周公旦 与当时的数学家商高的一段话。在这段话中,周公和商高讨论了关于 直角三角形的一些问题。其中就说到了“勾三股四弦五”的问题。 周公问商高:“我听说您很精通于数,请问数是从哪里来的呢?” 小学生经典数学故事《谁ZUI先发现了勾股定理》:商高回答说:“数的艺术是从研究圆形和方形中开始的,圆形是由方形产生的,而 方形是由折成直角的矩尺产生的。在研究矩形前需要知道九九口诀, 设想把一个矩形沿对角线切开,使得短直角边(勾)的长度为3,长直角边(股)的长度为4,斜边(弦)长则为5,并用四个上述直角三角形一样 的半矩形把它围起来拼成一个方形盘,从它的总面积49中减去由勾股 弦均分别为3、4、5的四个直角三角形构成的两个矩形的面积24,便 得到ZUI初所作正方形的面积25,这种方法称为‘积矩’。” 商高对“勾三股四弦五”的描述,已经具备了勾股定理的所有条件。而我们已经讲过的毕达哥拉斯发现勾股定理的年代是比周朝的商 高要晚的,所以证明,我国的数学家商高是ZUI早发现勾股定理的人。而“勾股定理”一开始也叫“勾股弦定理”,这也形象地点明了这个 定理的具体内容。 【篇二】 1.如果直角三角形的三条边长分别为2、4、a,那么a的取值能够有() A.0个 B.1个 C.2个 D.3个
五年级奥数几何勾股定理与弦图C级学生版
勾股定理与弦图 课前预习 华盛顿的傍晚 亲爱的小朋友们:他潜心探讨,有一位中年人,他聪明又勤奋,“在那山的那边海的那边的美国首都华盛顿, 年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年他反复思考与演算……”,那是1876人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然时而小声探讨。有两个小孩正在聚精会神地谈论着什么,时而大声争论,发现附近的一个小石凳上,由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男于是加菲尔德便问他们在干什么?那个小男孩头孩正俯着身子用树枝在地上画着一个直角三角形。,那么斜边长为多少呢?”43也不抬地说:“请问先生,如果直角三角形的两条直角边分别为和,那么这个直角三角7加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和的7形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很他经过反复思考与演算,不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。终于弄清了其中的道理,并给出了简洁的证明方法。具体方法如下:,△BDE可以拼成直角梯形ACDE△两个全等的RtABC和Rt 则梯形面积等于三个直角三角形面积之和。即DE)×CD÷2=AC×BC÷2+(AC+BD×DE÷2+AB×BE÷2 2÷2=a×b÷2+)a×b÷2+c×c÷2 +(ab222bca化简整理得=+
.2÷高×下底)+(上底,和梯形的面积公式:2÷高×点评:此种解法主要利用了三角形的面积公式:底. 而在我国对于勾股定理的证明又做出了那些贡献哪? 在我国古代,把直角三角形叫做勾股形。把直角三角形的较短直角边称为“勾”,较长直角边为“股”,斜边称为“弦”,所以把这个定理称为“勾股定理”。勾股定理揭示了直角三角形边之间的关系。即:在直角三角形中俩条直角边的平方和等于斜边的平方。公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘.得成三、四、五. ,:弦图又可以句股相乘为朱实二即弦.案开方除之三国时期的赵爽注解道:句股各自乘,并之为弦实,, ,亦成弦实.以句股之差自相乘为中黄实,加差之倍之为朱实四,
五年级奥数几何专项九 勾股定理与弦图(二)
专项九勾股定理与弦图(二) 课前预习 华盛顿的傍晚 亲爱的小朋友们: “在那山的那边海那边的美国首都华盛顿,有一位中年人,他聪明又勤奋,他潜心探讨,他反复思考与演算……”那是1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德 便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 具体方法如下: 两个全等的Rt△ABC和Rt△BDE可以拼成直角梯形ACDE, 则梯形面积等于三个直角三角形面积之和。即 (AC+DE)×CD÷2=AC×BC÷2+BD×DE÷2+AB×BE÷2 (a+b)2÷2=a×b÷2+a×b÷2+c×c÷2 化简整理得a2+b2=c2
点评:此种解法主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2. 而在我国对于勾股定理的证明又做出了那些贡献哪? 在我国古代,把直角三角形叫做勾股形。 把直角三角形的较短直角边称为“勾”,较长直角边为“股”,斜边称为“弦”,所以把这个定理称为“勾股定理”。勾股定理揭示了直角三角形边之间的关系。即:在直角三角形中俩条直角边的平方和等于斜边的平方。 公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘.得成三、四、五. 三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实. 汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句,长面曰股,相与结角曰弦.句短其股,股短其弦. 句股各自乘,并,而开方除之,即弦.
五年级奥数.几何.勾股定理与弦图(A级).学生版
华盛顿的傍晚 亲爱的小朋友们: “在那山的那边海那边的的美国首都华盛顿,有一位中年人,他聪明又勤奋,他潜心探讨,他反复思考与演算……,那是1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。 具体方法如下: 两个全等的Rt △ ABC 和Rt △BDE 可以拼成直角梯形ACDE , 则梯形面积等于三个直角三角形面积之和。即 (AC +DE )×CD÷2=AC×BC÷2+BD×DE÷2+AB×BE÷2 (a +b )2 ÷2=a×b÷2+a×b÷2+c×c÷2 化简整理得a 2 +b 2 =c 2 课前预习 勾股定理与弦图
点评:此种解法主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2. 而在我国对于勾股定理的证明又做出了那些贡献哪? 在我国古代,把直角三角形叫做勾股形。 把直角三角形的较短直角边称为“勾”,较长直角边为“股”,斜边称为“弦”,所以把这个定理称为“勾股定理”。勾股定理揭示了直角三角形边之间的关系。即:在直角三角形中俩条直角边的平方和等于斜边的平方。公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘. 得成三、四、五. 三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实. 汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句,长面曰股,相与结角曰弦.句短其股,股短其弦. 句股各自乘,并,而开方除之,即弦. 勾股定理的证明:
2018最新五年级奥数.几何.勾股定理与弦图(C级).学生版
课前预习 华盛顿的傍晚 亲爱的小朋友们: “在那山的那边海的那边的美国首都华盛顿,有一位中年人,他聪明又勤奋,他潜心探讨,他反复思考与演算……”,那是1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,加菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。具体方法如下: 两个全等的Rt △ABC 和Rt △BDE 可以拼成直角梯形ACDE ,则梯形面积等于三个直角三角形面积之和。即 (AC +DE )×CD÷2=AC×BC÷2+BD×DE÷2+AB×BE÷2 (a +b )2÷2=a×b÷2+a×b÷2+c×c÷2 化简整理得a 2+b 2=c 2 点评:此种解法主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2.勾股定理与弦图
小学奥数勾股定理与弦图讲解
第十二讲勾股定理与弦图 【教学重难点】 能够用弦图证明勾股定理的具体内容,并运用勾股定理解决相应的几何问题。【教学内容】 勾股定理是一个基本的几何定理。直角三角形两直角边(即 “勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2o 勾股定理 第一部分:勾股定理的应用 H 介绍一种神奇的无字证明 b
10 【例1】(★★) 求下面各三角形中未知边的长度。 【例2】(★★★) 有一个直角边为1和1的直角三角形,以它的斜边和1为直角边, 向外作另一个直角三角形。重复以上操作,如下图。求第 1023个直 角三角形的斜边长度是 _________ 。第 _____ 个直角三角形的斜边长度是 17 【例3】(★★★) 根据图中所给的条件,求梯形 ABCD 勺面积 【例4】(★★★) A I)
【例5】(★★★★) 第二部分:介绍弦图及其应用 ⑴大正方形边长为:a + b ⑵小正方形边长为:a — b ⑶中正方形边长为: c 【例6】(★★★) 一个直角三角形的斜边长8厘米,两个直角边的长度差为 2厘 如图,请根据所给的条件,计算出大梯形的面积(单位:厘米) 如图,在四边形 ABCD 中,AB= 30 ,AD= 48, BC= 14 , CD= 40,/ ADBk Z DB G 90°。请问:四边形 ABCD 的面积是多少? O B (基本思想是图形经过割补后,面积不变)
【例7 ] ( ★★★★★) 从一块正方形玻璃上裁下宽为16分米的一长方形条后,剩下的那块 长方形的面积为336平方分米,原来正方形的面积是多少平方分米? 自我检测 1.将长为10米的梯子斜靠在墙上,若梯子上端到墙的底端距离为6 米,则梯足到墙的底端距离为 _______________ . 2.若直角三角形一直角边和斜边分别为17和145,则另一直角边 为_____________ 。 3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方 米,求这个三角形的面积?
奥数专题:勾股定理与弦图
勾股定理与弦图 【教学重难点】 能够用弦图证明勾股定理的具体内容,并运用勾股定理解决相应的几何问题。 【教学内容】 勾股定理是一个基本的几何定理。直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2。 介绍一种神奇的无字证明 第一部分:勾股定理的应用 【例 1】(★★) 求下面各三角形中未知边的长度。
【例 2】(★★★) 有一个直角边为 1 和1 的直角三角形,以它的斜边和1 为直角边,向外作另一个直角三角形。重复以上操作,如下图。求第1023 个直角三角形的斜边长度是_____。第_____个直角三角形的斜边长度是 17。 【例 3】(★★★) 根据图中所给的条件,求梯形ABCD 的面积。 【例 4】(★★★) 如图,请根据所给的条件,计算出大梯形的面积(单位:厘米)。
【例5】(★★★★) 如图,在四边形ABCD 中,AB=30 ,AD=48,BC=14 ,CD=40,∠ADB+∠DBC=90°。请问:四边形ABCD 的面积是多少? 第二部分:介绍弦图及其应用 (基本思想是图形经过割补后,面积不变) ⑴大正方形边长为:a+b ⑵小正方形边长为:a-b ⑶中正方形边长为:c 【例 6】(★★★) 一个直角三角形的斜边长 8 厘米,两个直角边的长度差为2 厘米,求这个三角形的面积?
【例 7】(★★★★★) 从一块正方形玻璃上裁下宽为16 分米的一长方形条后,剩下的那块长方形的面积为336 平方分米,原来正方形的面积是多少平方分米? 自我检测 1.将长为10 米的梯子斜靠在墙上,若梯子上端到墙的底端距离为6 米,则梯足到墙的底端距离为__________米. 2.若直角三角形一直角边和斜边分别为17 和145 ,则另一直角边 为___________。 3.已知一个直角三角形的两边长分别为3 和4,则第三边长的平方 是。 4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为___________cm2.
小学奥数华杯赛几何之勾股定理与弦图
小学奥数华杯赛几何之勾股定理与弦图 【篇一】 关于勾股定理,我们已经谈过很多了。中国、希腊、埃及这些文明古国,处于不同的地区,然而却都很早地,独立地发现了勾股定理。那么,勾股定理到底是谁最先发现的呢?我们可以自豪地说:是我们中国人最先发现的。证据就是《周髀算经》中的记载。 《周髀算经》一开始,就记载了我国周朝初年的大政治家周公旦与当时的数学家商高的一段话。在这段话中,周公和商高讨论了关于直角三角形的一些问题。其中就说到了“勾三股四弦五”的问题。 周公问商高:“我听说您很精通于数,请问数是从哪里来的呢?” 小学生经典数学故事《谁最先发现了勾股定理》:商高回答说:“数的艺术是从研究圆形和方形中开始的,圆形是由方形产生的,而方形是由折成直角的矩尺产生的。在研究矩形前需要知道九九口诀,设想把一个矩形沿对角线切开,使得短直角边(勾)的长度为3,长直角边(股)的长度为4,斜边(弦)长则为5,并用四个上述直角三角形一样的半矩形把它围起来拼成一个方形盘,从它的总面积49中减去由勾股弦均分别为3、4、5的四个直角三角形构成的两个矩形的面积24,便得到最初所作正方形的面积25,这种方法称为‘积矩’。” 商高对“勾三股四弦五”的描述,已经具备了勾股定理的所有条件。而我们已经讲过的毕达哥拉斯发现勾股定理的年代是比周朝的商高要晚的,所以证明,我国的数学家商高是最早发现勾股定理的人。而“勾股定理”一开始也叫“勾股弦定理”,这也形象地点明了这一定理的
具体内容。 【篇二】 1.如果直角三角形的三条边长分别为2、4、a,那么a的取值可以有( ) A.0个 B.1个 C.2个 D.3个 答案:C 说明:①若a为斜边长,则由勾股定理有22+42=a2,可得a=2;②若a为直角边长,则由勾股定理有22+a2=42,可得a=2,所以a的取值可以有2个,答案为C. 2.小明搬来一架2.5米长的木梯,准备把拉花挂在2.4米高的墙上,则梯脚与墙脚的距离为( )米 A.0.7 B.0.8 C.0.9 D.1.0 答案:A 说明:因为墙与地面的夹角可看作是直角,所以利用勾股定理,可得出梯脚与墙脚的距离为===0.7,答案为A. 3.一个直角三角形的斜边长比直角边长大2,另一直角边长为6,则斜边长为( ) A.6 B.8 C.10 D.12 答案:C 说明:设直角边长为x,则斜边为x+2,由勾股定理得x2+62=(x+2)2,解之得x=8,所以斜边长为8+2=10,答案为C. 【篇三】
