初二数学经典题型(含答案)

初二数学经典题型
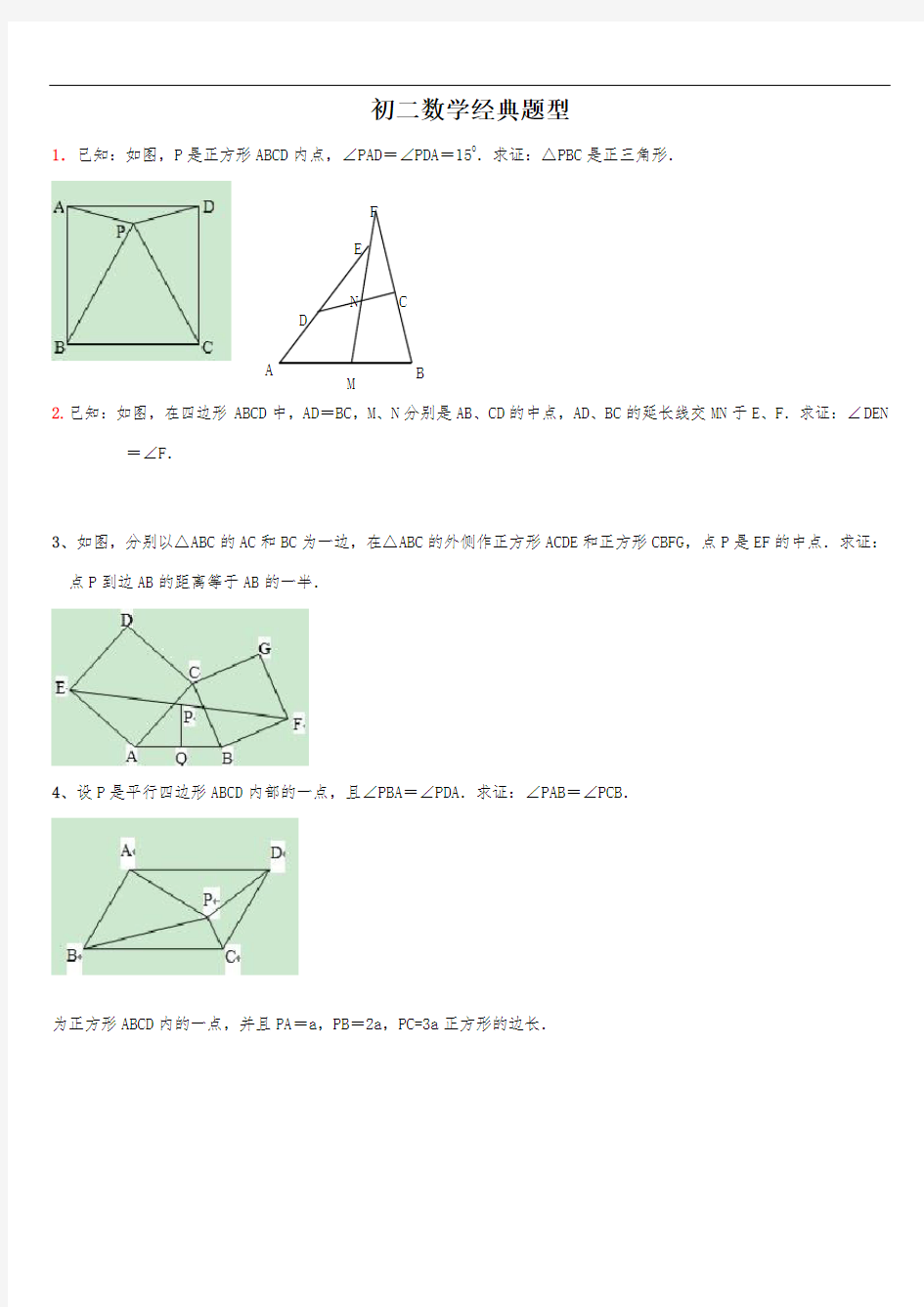
1.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150
.求证:△PBC 是正三角形.
2.已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN
=∠F .
3、如图,分别以△ABC
的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边
AB 的距离等于AB 的一半.
4、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .
为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC=3a 正方形的边长.
A
N
F E C
D
M
B
A P
C
D
B
6.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB . (1)求证:① PE=PD ; ② PE ⊥PD ; (2)设AP =x , △PBE 的面积为y .
① 求出
y 关于x 的函数关系式,并写出x 的取值范围; ② 当x 取何值时,y 取得最大值,并求出这个最大值.
答案
1、证明如下。
首先,PA=PD ,∠PAD=∠PDA=(180°-150°)÷2=15°,∠PAB=90°-15°=75°。
在正方形ABCD 之外以AD 为底边作正三角形ADQ , 连接PQ , 则
∠PDQ=60°+15°=75°,同样∠PAQ=75°,又AQ=DQ,,PA=PD ,所以△PAQ ≌△PDQ , 那么∠PQA=∠PQD=60°÷2=30°,在△PQA 中,
∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB ,于是PQ=AQ=AB , 显然△PAQ ≌△PAB ,得∠PBA=∠PQA=30°,
PB=PQ=AB=BC ,∠PBC=90°-30°=60°,所以△ABC 是正三角形。
2、证明:连接AC,并取AC 的中点G,连接GF,GM.
又点N 为CD 的中点,则GN=AD/2;GN ∥AD,∠GNM=∠DEM;(1) 同理:GM=BC/2;GM ∥BC,∠GMN=∠CFN;(2)
又AD=BC,则:GN=GM,∠GNM=∠GMN.故:∠DEM=∠CFN.
3、证明:分别过E 、C 、F 作直线AB 的垂线,垂足分别为M 、O 、N ,
F
在梯形MEFN 中,WE 平行NF 因为P 为EF 中点,PQ 平行于两底 所以PQ 为梯形MEFN 中位线, 所以PQ =(ME +NF )/2
又因为,角0CB +角OBC =90°=角NBF +角CBO 所以角OCB=角NBF 而角C0B =角Rt =角BNF CB=BF
所以△OCB 全等于△NBF △MEA 全等于△OAC (同理) 所以EM =AO ,0B =NF 所以PQ=AB/2.
4、过点P 作DA 的平行线,过点A 作DP 的平行线,两者相交于点E ;连接BE
因为DP 解:(1)证法一:
① ∵ 四边形ABCD 是正方形,AC 为对角线, ∴ BC=DC , ∠BCP =∠DCP=45°. ∵ PC =PC ,
∴ △PBC ≌△PDC (SAS ). ∴ PB = PD , ∠PBC =∠PDC . 又∵ PB = PE ,
∴ PE =PD .
② (i )当点E 在线段BC 上(E 与B 、C 不重合)时, ∵ PB =PE , ∴ ∠PBE =∠PEB , ∴ ∠PEB =∠PDC ,
∴ ∠PEB +∠PEC =∠PDC +∠PEC =180°, ∴ ∠DPE =360°-(∠BCD +∠PDC +∠PEC )=90°, ∴ PE ⊥PD . )
A B
C D
P
E
1
2
H
(ii )当点E 与点C 重合时,点P 恰好在AC 中点处,此时,PE ⊥PD . (iii )当点E 在BC 的延长线上时,如图. ∵ ∠PEC =∠PDC ,∠1=∠2, ∴ ∠DPE =∠DCE =90°, ∴ PE ⊥PD .
综合(i )(ii )(iii ), PE ⊥PD .
(2)① 过点P 作PF ⊥BC ,垂足为F ,则BF =FE . ∵ AP =x ,AC =2, ∴ PC =2- x ,PF =FC =x x 2
2
1)2(22-=-. BF =FE =1-FC =1-(x 2
2
1-)=x 22. ∴ S △PBE =BF ·PF =
x 22(x 2
2
1-)x x 22212+-=. 即 x x y 22
212+-= (0<x <2).
② 41
)22(21222122+--=+-=x x x y .
∵ 2
1
-=a <0,
∴ 当22=x 时,y 最大值4
1
=.
(1)证法二:① 过点P 作GF ∥AB ,分别交AD 、BC 于G 、F . 如图所示. ∵ 四边形ABCD 是正方形,
∴ 四边形ABFG 和四边形GFCD 都是矩形,
△AGP 和△PFC 都是等腰直角三角形.
∴ GD=FC =FP ,GP=AG =BF ,∠PGD =∠PFE =90°. 又∵ PB =PE ,
∴ BF =FE , ∴ GP =FE ,
∴ △EFP ≌△PGD (SAS ). ∴ PE =PD .
A
B C
P
D
E
F A
B
C
P
D
E
F G
1
2
3
② ∴ ∠1=∠2.
∴ ∠1+∠3=∠2+∠3=90°. ∴ ∠DPE =90°.
∴ PE ⊥PD . (2)①∵ AP =x , ∴ BF =PG =x 22,PF =1-x 2
2.
∴ S △PBE =BF ·PF =
x 22(x 2
21-)x x 22212+-=. 即 x x y 22
212+-= (0<x <2).
② 41
)22(21222122+--=+-=x x x y .
∵ 2
1
-=a <0,
∴ 当22=
x 时,y 最大值4
1=.
26.(本小题满分8分)
如图1,在四边形ABCD 中,AB CD =,E F 、分别是BC AD 、的中点,连结EF 并延长,分别与BA CD 、的延长线交于点M N 、,则BME CNE ∠=∠(不需证明).
(温馨提示:在图1中,连结BD ,取BD 的中点H ,连结HE HF 、,根据三角形中位线定理,证明HE HF =,从而12∠=∠,再利用平行线性质,可证得BME CNE ∠=∠.)
问题一:如图2,在四边形ADBC 中,AB 与CD 相交于点O ,AB CD =,E F 、分别是BC AD 、的中点,连结EF ,分别交DC AB 、于点M N 、,判断OMN △的形状,请直接写出结论.
问题二:如图3,在ABC △中,AC AB >,D 点在AC 上,AB CD =,E F 、分别是BC AD 、的中点,连结EF 并延长,与BA 的延长线交于点G ,若60EFC ∠=°,连结GD ,判断AGD △的形状并证明.
A
C B D
F E N
M O E
B
C D
H A F N M 1 2
图1
图2
图3
A
B
C
D
F G E
26.(1)等腰三角形 ···························· 1分 (2)判断出直角三角形 ·························· 1分 证明:如图连结BD ,取BD 的中点H ,连结HF HE 、, ··········· 1分
F 是AD 的中点,
HF AB ∴∥,1
2
HF AB =
, 13∴∠=∠.
同理,1
2
HE CD HE CD =
∥,, 2EFC ∴∠=∠.
AB CD =,
∴HF HE =,
12∴∠=∠.
······························· 1分 60EFC ∠=°,
360EFC AFG ∴∠=∠=∠=°,
AGF ∴△是等边三角形. ························· 2分 AF FD =,
GF FD ∴=,
30FGD FDG ∴∠=∠=°
90AGD ∴∠=°
即AGD △是直角三角形. ························· 2分
A B
C
D F G H
E
1 2
3
