中考数学专题复习_几何探究题

专题复习几何探究问题

一、结论探究

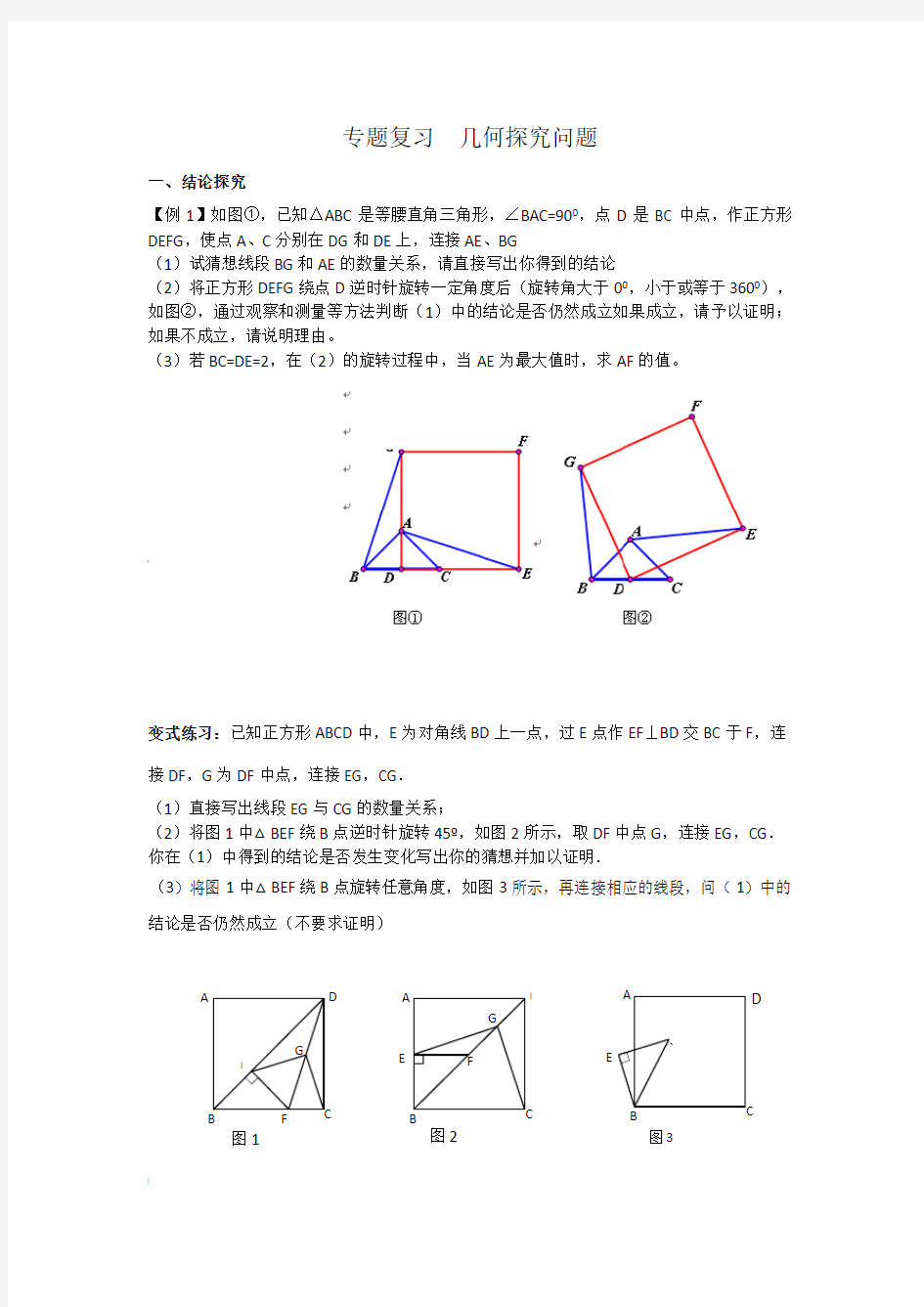
【例1】如图①，已知△ABC是等腰直角三角形，∠BAC=900，点D是BC中点，作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG

（1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论

（2）将正方形DEFG绕点D逆时针旋转一定角度后（旋转角大于00，小于或等于3600），如图②，通过观察和测量等方法判断（1）中的结论是否仍然成立如果成立，请予以证明；如果不成立，请说明理由。

（3）若BC=DE=2，在（2）的旋转过程中，当AE为最大值时，求AF的值。

'

变式练习：已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

（1）直接写出线段EG与CG的数量关系；

（2）将图1中△BEF绕B点逆时针旋转45o，如图2所示，取DF中点G，连接EG，CG．你在（1）中得到的结论是否发生变化写出你的猜想并加以证明．

（3）将图1中△BEF绕B点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立（不要求证明）

| A D

]

G

图1

F

A[

E

G

图2

、

A

E

图3

D

F

E

C B

A

B'

C'

二、条件探究

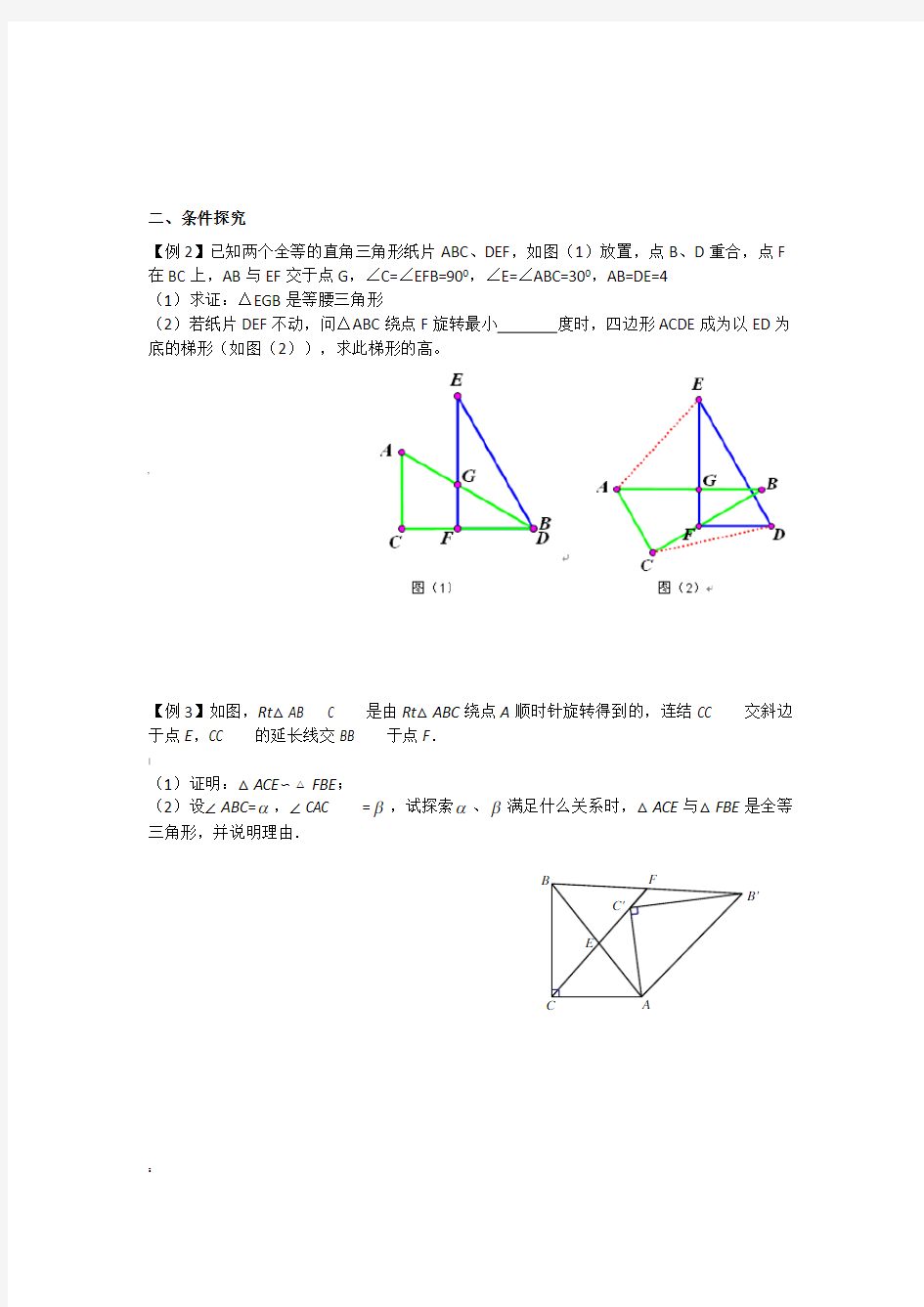
【例2】已知两个全等的直角三角形纸片ABC 、DEF ，如图（1）放置，点B 、D 重合，点F 在BC 上，AB 与EF 交于点G ，∠C=∠EFB=900，∠E=∠ABC=300，AB=DE=4 （1）求证：△EGB 是等腰三角形

（2）若纸片DEF 不动，问△ABC 绕点F 旋转最小 度时，四边形ACDE 成为以ED 为底的梯形（如图（2）），求此梯形的高。

,

【例3】如图，Rt △AB C 是由Rt △ABC 绕点A 顺时针旋转得到的，连结CC 交斜边

于点E ，CC 的延长线交BB 于点F ． |

（1）证明：△ACE ∽△FBE ；

（2）设∠ABC =α，∠CAC =β，试探索α、β满足什么关系时，△ACE 与△FBE 是全等三角形，并说明理由．

；

E

图1

A

:

C

D

图2

三、类比探究 【例4】

（1）操作发现：如图，矩形ABCD 中，E 是AD 的中点，将△ABE 沿BE 折叠后得到△GBE ，且点G 在举行ABCD 内部．小明将BG 延长交DC 于点F ，认为GF =DF ，你同意吗说明理由． （2）问题解决：保持（1）中的条件不变，若DC =2DF ，求

AB

AD

的值； /

（3）类比探求：保持（1）中条件不变，若DC =nDF ，求AB

AD

的值．

【例5】如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．如，平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线．

（1）三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________；

（

（2）如图1，梯形ABCD 中，AB ∥DC ，如果延长DC 到E ，使CE ＝AB ，连接AE ，那么有S 梯

形ABCD

＝S △ABE ．请你给出这个结论成立的理由，并过点A 作出梯形ABCD 的面积等分线（不

写作法，保留作图痕迹）；

（3）如图，四边形ABCD 中，AB 与CD 不平行，S △ADC ＞S △ABC ，过点A 能否作出四边形ABCD 的面积等分线若能，请画出面积等分线，并给出证明；若不能，说明理由．

A

B

。

【例6】

（1）如图1，在正方形ABCD 中，M 是BC 边（不含端点B 、C ）上任意一点,P 是BC 延长线上一点，N 是∠DCP 的平分线上一点．若∠AMN =90°，求证：AM =MN ．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明． 证明：在边AB 上截取AE =MC ，连ME ．正方形ABCD 中，∠B =∠BCD =90°，

AB =BC ．∴∠NMC =180°—∠AMN —∠AMB =180°—∠B —∠AMB =∠MAB =∠MAE ．（下面请你完成余下的证明过程）

（2）若将（1）中的“正方形ABCD ”改为“正三角形ABC ”（如图2）,N 是∠ACP 的平分线上一点，则当∠AMN =60°时，结论AM =MN 是否还成立请说明理由． ~

（3）若将（1）中的“正方形ABCD ”改为“正n 边形ABCD …X ”，请你作出猜想：当∠AMN = °时，结论AM =MN 仍然成立．（直接写出答案，不需要证明）

{

【例7】请阅读下列材料

问题：如图1，在等边三角形ABC 内有一点P ，且PA=2， PB=3， PC=1．求∠BPC 度数的大小和等边三角形ABC 的边长．

李明同学的思路是：将△BPC 绕点B 顺时针旋转60°，画出旋转后的图形（如图2）．连接PP′，可得△P′PC 是等边三角形，而△PP′A 又是直角三角形（由勾股定理的逆定理可证）．所以∠AP′C=150°，而∠BPC=∠AP′C=150°．进而求出等边△ABC 的边长为7．问题得到解决．

请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD 内有一点P ，

M N P D C

E

B A

图1

M N

P C B A 图2

且PA=5，BP=2，PC=1．求∠BPC 度数的大小和正方形ABCD 的边长．

能力检测

@

1．如图1，已知∠ABC =90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结 QE 并延长交射线BC 于点F .

（1）如图2，当BP =BA 时，∠EBF = °，猜想∠QFC = °；

（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明； （3）已知线段AB =32，设BP =x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．

~

2．如图（1），在△ABC 和△EDC 中，AC ＝CE ＝CB ＝CD ，∠ACB ＝∠ECD ＝

90，AB 与CE 交于F ，ED 与AB 、BC 分别交于M 、H ． （1）求证：CF ＝CH ；

（2）如图（2），△ABC 不动，将△EDC 绕点C 旋转到∠BCE =

45时，试判断四边形ACDM 是什么四边形并证明你的结论．

（

图2

A

B

E <

Q P F C 图1

A

C

B

E

[

Q

F P A C D B M

— F H 图（1） A C D

B

（ E F

H

图（2） 图3

)

图2

3、如图（1）已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连接EB，过点A作AM⊥BE于M，AM交BD于点F

（1）求证：OE=OF

（2）如图（2）若点E在AC的延长线上，AM⊥BE于M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗如果成立，请给出证明；如果不成立，请说明理由。

4．已知：如图，在梯形ABCD中，AD∥BC，∠DCB = 90°，E是AD的中点，点P是BC边上的动点（不与点B重合），EP与BD相交于点O.

(

（1）当P点在BC边上运动时，求证：△BOP∽△DOE；

（2）设（1）中的相似比为k，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形①当k= 1时，是；②当k= 2时，

是；③当k= 3时，是. 并证明

．．．k= 2时的结论.

—

5．

观察思考：

某种在同一平面进行传动的机械装置如图14-1，图14-2

是它的示意图．其工作原理是：滑块Q在平直滑道l上可

以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，

并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两

连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为

进一步研究其中所蕴含的数学知识，过点O作OH ⊥l于点

H，并测得OH =4分米，PQ = 3分米，OP = 2分米．

解决问题：

A

B

D

E

O

l

%

P

图14-2

图14-1

连杆

滑块

滑道

D

E

》

A

M

N C

B

（1）点Q 与点O 间的最小距离是 分米；点Q 与点O 间的最大距离是 分米；点Q 在l 上滑到最左端的位置与滑到最右端位置间的距离是 分米． （2）如图14-3，小明同学说：“当点Q 滑动到点H 的位 置时，PQ 与⊙O 是相切的．”你认为他的判断对吗为什么 （3）①小丽同学发现：“当点P 运动到OH 上时，点P 到l 的距

离最小．”事实上，还存在着点P 到l 距离最大的位置，此时，点P 到l 的距离是 分米；

②当OP 绕点O 左右摆动时，所扫过的区域为扇形，求这个扇

形面积最大时圆心角的度数．

！

6．(9分)如图，点C 为线段AB 上任意一点(不与点A 、B 重合)，分别以AC 、BC 为一腰在AB

的同侧作等腰△ACD 和△BCE ，CA ＝CD ，CB ＝CE ，∠ACD 与∠BCE 都是锐角，且∠ACD ＝∠BCE ，连接AE 交CD 于点M ，连接BD 交CE 于点N ，AE 与BD 交于点P ，连接CP ． (1)求证：△ACE ≌△DCB ；

(2)请你判断△ACM 与△DPM 的形状有何关系并说明理由； (3)求证：∠APC ＝∠BPC ．

、

部分答案

【变式练习】 解：（1）CG=EG ……………………… 1分 （2）（1）中结论没有发生变化，即EG=CG ．

证明：连接AG ，过G 点作MN ⊥AD 于M ，与EF 的延长线交于N 点． 在△DAG 与△DCG 中，

∵ AD=CD ，∠ADG=∠CDG ，D G=DG ， ∴ △DAG ≌△DCG ．

【 O 图14-3

P

&

A

D

E G M N

)

∴ AG=CG．………………………2分

在△DMG与△FNG中，

∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG．

∴ MG=NG …………………………3分

在矩形AENM中，AM=EN．……………4分

在Rt△AMG 与Rt△ENG中，

∵AM=EN，MG=NG，

∴△AMG≌△ENG．

，

∴ AG=EG．…………………………5分

∴EG=CG．……………………………6分

（3）（1）中的结论仍然成立．………………7分【例2】

【例3】

【例4】

F

A D

C E

图3

G

/

【例5】

解：（1）如图，将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．∴AP′=PC=1，BP=BP′=2．

连结P P′，

在Rt△BP′P中，

∵BP=BP′=2，∠P BP′=90°，

∴P P′=2，∠BP′P=45°．………………………………2分.

在△AP′P中，AP′=1，P P′=2，AP=5，

∵222

12(5)

+=，即AP′2 + PP′2 = AP2．

∴△AP′P是直角三角形，即∠A P′ P=90°．

∴∠AP′B=135°．

∴ ∠BPC=∠AP′B=135°． ………………………………………………… 4分 （2）过点B 作BE ⊥AP′ 交AP′ 的延长线于点E ． ∴ ∠E P′ B=45°. ∴ E P′=B E=1. ∴ AE=2.

∴ 在Rt △ABE 中，由勾股定理，得 ……………………………… 7分

%

∴ ∠BPC=135°

能力检测：

【题1】解: （1）=∠EBF 30° QFC ∠= 60°..................................2分 （2）QFC ∠=60°.....................................1分

不妨设BP , 如图1所示 ∵∠BAP=∠BAE+∠EAP=60°+∠EAP

∠EAQ=∠QAP+∠EAP=60°+∠EAP ∴∠BAP=∠EAQ..........................................2分 在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ

∴△ABP ≌△AEQ （SAS ）..............3分 ∴∠AEQ=∠ABP=90°....................4分 ∴∠BEF 180180906030AEQ AEB =?-∠-∠=?-?-?=?

∴QFC ∠=EBF BEF ∠+∠=3030?+?=60°…………………………............5分

(事实上当BP 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分） (3)在图1中，过点F 作FG ⊥BE 于点G

∵△ABE是等边三角形∴BE=AB=

3

2，由（1）得=

∠EBF

30°

在Rt

△BGF中，

3

2

BE

BG==

∴BF=

2

cos30

BG

=

?∴EF=2.......1分

∵△ABP≌△AEQ ∴QE=BP=x∴QF=QE＋EF2

x

=+................2分

过点Q作QH⊥BC，垂足为H

在Rt△QHF中，

3

sin60(2)

y QH QF x

==?=+

（x＞0）

即y关于x的函数关系式是：

3

3

2

y x

=+

.......................................................3分【题2】

【题4】

【题5】