(完整版)大连理工大学高等数值分析椭圆方程差分法

椭圆方程差分法
1 矩形网上差分方程
考虑二阶椭圆型偏微分方程的第一边值问题
(1.1) ()()()?????=∈=+++--Γy x y x u y x F Eu Du Cu u u y x yy xx ,,,αG
其中C ,E D ,是常数;0≥E ;()()G C 0,∈=y x F F ;(,)x y α是给定的光滑函数。假设(5.1)存在光滑的唯一解。
为简单起见,假设G 是矩形区域,其四个边与相应坐标轴平行。考虑矩形网格:1h 和2h 分别为x 和y 方向的步长,h G 为网格内点节点集合,h Γ为网格边界点集合,=h G h G Y h Γ。
对于内点()j i y x ,h G ∈用如下的差分方程逼近(1.1) (1.2)
21
,1,12h u u u j i ij j i -++---221,1,2h u u u j i ij j i -++-+1,1,12h u u C j i j i -+-+21,1,2h u u D j i j i -+-+ij Eu =ij F
其中),(j i ij y x F F =。(1.2)通常称为五点差分格式。
用(1.1)的真解(,)u x y 在网点上的值(,)i j u x y 、1(,)i j u x y -等等分别替换(1.2)
中的ij u 、1,i j u -等等,然后在(,)i j x y 点处作Tailor 展开,便知(1.2)逼近(1.1)
的截断误差阶为()22
21h h O +。 方程(1.2)可以改写为
(1.3) j i a ,1-j i u ,1-+j i a ,1+j i u ,1++1,-j i a 1,-j i u +1,+j i a 1,+j i u +j i a ,j i u ,ij F = 对每一内点都可以列出这样一个方程。遇到边界点时,因为边界点u 的函数值已知,将相应的项挪到右端去。最后,得到一个以u 的内点近似值为未知数的线性方程组。这个方程组是稀疏的,并且当1h 和2h 足够小时是对角占优的。 可以证明,五点差分格式关于右端和初值都是稳定的,收敛阶为2212()O h h +。
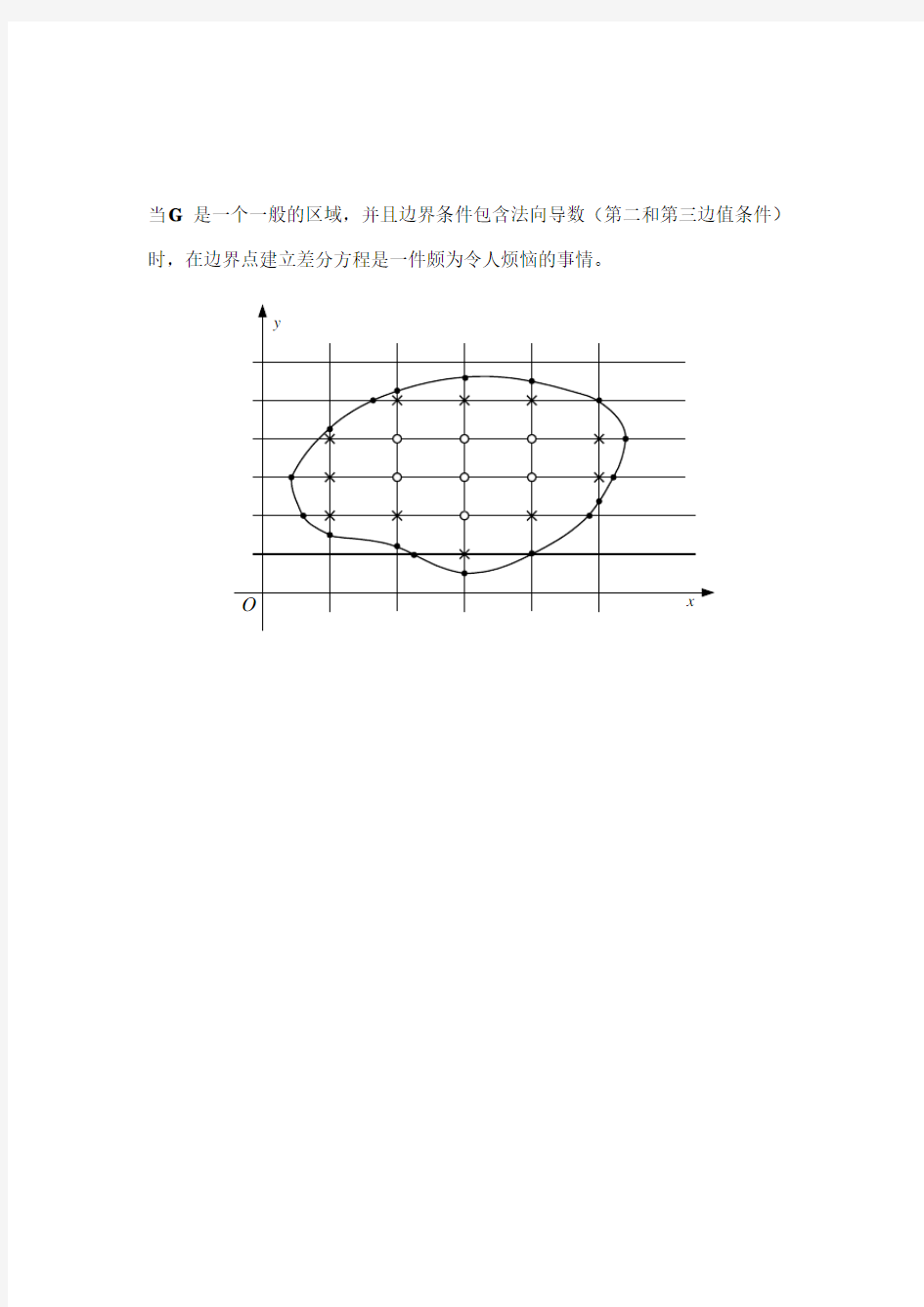
当G是一个一般的区域,并且边界条件包含法向导数(第二和第三边值条件)时,在边界点建立差分方程是一件颇为令人烦恼的事情。
五点差分法(matlab)解椭圆型偏微分方程教学文稿
用差分法解椭圆型偏微分方程 -(Uxx+Uyy)=(pi*pi-1)e^xsin(pi*y) 0 在科学技术各领域中,有很多问题都可以归结为偏微分方程问题。在物理专业的力学、热学、电学、光学、近代物理课程中都可遇见偏微分方程。 偏微分方程,再加上边界条件、初始条件构成的数学模型,只有在很特殊情况下才可求得解析解。随着计算机技术的发展,采用数值计算方法,可以得到其数值解。 偏微分方程基本形式 而以上的偏微分方程都能利用PDE工具箱求解。 PDE工具箱 PDE工具箱的使用步骤体现了有限元法求解问题的基本思路,包括如下基本步骤: 1) 建立几何模型 2) 定义边界条件 3) 定义PDE类型和PDE系数 4) 三角形网格划分 5) 有限元求解 6) 解的图形表达 以上步骤充分体现在PDE工具箱的菜单栏和工具栏顺序上,如下 具体实现如下。 打开工具箱 输入pdetool可以打开偏微分方程求解工具箱,如下 首先需要选择应用模式,工具箱根据实际问题的不同提供了很多应用模式,用户可以基于适 当的模式进行建模和分析。 在Options菜单的Application菜单项下可以做选择,如下 或者直接在工具栏上选择,如下 列表框中各应用模式的意义为: ① Generic Scalar:一般标量模式(为默认选项)。 ② Generic System:一般系统模式。 ③ Structural Mech.,Plane Stress:结构力学平面应力。 ④ Structural Mech.,Plane Strain:结构力学平面应变。 ⑤ Electrostatics:静电学。 ⑥ Magnetostatics:电磁学。 ⑦ Ac Power Electromagnetics:交流电电磁学。 ⑧ Conductive Media DC:直流导电介质。 ⑨ Heat Tranfer:热传导。 ⑩ Diffusion:扩散。 可以根据自己的具体问题做相应的选择,这里要求解偏微分方程,故使用默认值。此外,对于其他具体的工程应用模式,此工具箱已经发展到了Comsol Multiphysics软件,它提供了更强大的建模、求解功能。 另外,可以在菜单Options下做一些全局的设置,如下 l Grid:显示网格 l Grid Spacing…:控制网格的显示位置 l Snap:建模时捕捉网格节点,建模时可以打开 l Axes Limits…:设置坐标系范围 l Axes Equal:同Matlab的命令axes equal命令 建立几何模型 使用菜单Draw的命令或使用工具箱命令可以实现简单几何模型的建立,如下 各项代表的意义分别为 用五点有限差分格式求解椭圆型方程(偏微分方程)程序2 2010-04-29 10:33 function varargout=liu(varargin) a=0;b=2;c=0;d=1;h1=1/16;h2=1/16; f=inline('(pi^2-1)*exp(x)*sin(pi*y)','x','y'); g1x=inline('0'); g2x=inline('0'); g1y=inline('sin(pi*y)'); g2y=inline('exp(2)*sin(pi*y)'); [X,Y,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2); mesh(X,Y,Z); shading flat; xlabel('X','FontSize',14); ylabel('Y','FontSize',14); zlabel('error','FontSize',14); title('误差图'); function [X,T,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2) %求解下问题 %-(u_xx+u_yy)=f(x,y) x,y 在区域内x in a %h2离散y方向的步长 N=10000; x=a:h1:b; y=c:h2:d; m=length(x); n=length(y); ee=0.00001; [X,T]=meshgrid(x,y); Z=zeros(n,m); U=zeros(n,m); for i=2:m-1 U(1,i)=feval(g1x,x(i)); U(n,i)=feval(g2x,x(i)); end for j=1:n U(j,1)=feval(g1y,y(j)); U(j,m)=feval(g2y,y(j)); end %while true %下为高斯赛德尔迭代法 %---------------------------------------------------------------------- for k=1:N 课程名称(中文):偏微分方程数值解专题 课程名称(英文):Some topics on numerical solutions of partial differential equations 一)课程目的和任务:有限差分方法是微分方程定解问题的最广泛的数值方法之一,其基本思想是用差商近似代替导数,用有限个未知量的差分方程组的解作为微分方程定解问题的解。本课程旨在介绍非线性抛物和椭圆型方程的有限差分方法的最新进展,并简单介绍在实际模型问题中的应用。 本课程是为计算数学专业二年级研究生开设的一门专业选修课程,也可作为其它专业研究生的选修课程。其主要目的是使学生了解不同非线性定解问题的有限差分格式的构造方法,掌握有限差分方法的基本理论和一些数值分析技巧,使他们对这一方法能够有清晰和全面的了解,并能应用于实际问题的数值模拟和数值计算。通过对本课程的学习,进一步丰富微分方程定解问题的数值方法,掌握有限差分方法的最新进展,也为学习进一步的专业知识打下坚实的基础。 主要内容:本课程以非线性抛物型和椭圆型方程的定解问题为例,介绍有限差分格式的构造方法,同时介绍相应数值分析的基本方法和技巧,也简单讨论有限差分解的一些性质。所有内容基本都是本课题的最新研究进展。具体内容如下: 第一章:非线性椭圆边值问题的有限差分方法。本章主要介绍非线性椭圆边值问题的差分解法,给出一些定性分析,包括解的存在唯一性、收敛性和误差估计,同时介绍分析非线性差分方程组的上下解方法以及求解的单调迭代算法; 第二章:非线性抛物初边值问题的有限差分方法。本章主要介绍非线性抛物边值问题的差分解法,包括一些定性分析,如解的存在唯一性、收敛性和误差估计,同时介绍分析非线性差分方程组的上下解方法以及求解的单调迭代算法; 第三章:依赖于时间数值解的渐近性。本章着重介绍非线性抛物初边值问题有限差分解的长时间渐近性,稳定性及在实际模型问题中的应用; 第四章:非线性椭圆方程组的有限差分方法。本章主要介绍非线性椭圆型方程组的有限差分解法,着重介绍分析非线性差分方程组的上下解方法以及求解的单调迭代算法。 第五章:非线性抛物方程组的有限差分方法。本章主要介绍非线性抛物型方程组的有限差分解法,介绍分析非线性差分方程组的上下解方法以及求解的单调迭代算法。除此之外,还介绍特别介绍有限差分解的长时间渐近性,稳定性及在实际模型问题中的应用。 二)预备知识:数值代数、数值逼近、微分方程数值解、泛函分析。 三)教材及参考书目: 教材:自编讲义,2012. 参考书目:1) C.V. Pao, Nonlinear Parabolic and Elliptic Equations, Plenum Press, New York, 1992. 2) A. Berman, R. Plemmons, Nonnegative Matrix in the Mathematical Science, Academic Press, New York, 1979. 四)讲授大纲(中英文) 第一章非线性椭圆边值问题的有限差分方法 1)有限差分方程 2)上下解方法 3)单调迭代算法 4)上下解的构造方法 两点边值问题有限元法(必做) 从Galerkin 原理出发用线性元解两点边值问题: "2,01(0)(1)0u u x x u u ?-+=< 有限差分法的Matlab程序(椭圆型方程) function FD_PDE(fun,gun,a,b,c,d) % 用有限差分法求解矩形域上的Poisson方程 tol=10^(-6); % 误差界 N=1000; % 最大迭代次数 n=20; % x轴方向的网格数 m=20; % y轴方向的网格数 h=(b-a)/n; % x轴方向的步长 l=(d-c)/m; % y轴方向的步长 for i=1:n-1 x(i)=a+i*h; end % 定义网格点坐标 for j=1:m-1 y(j)=c+j*l; end % 定义网格点坐标 u=zeros(n-1,m-1); %对u赋初值 % 下面定义几个参数 r=h^2/l^2; s=2*(1+r); k=1; % 应用Gauss-Seidel法求解差分方程 while k<=N % 对靠近上边界的网格点进行处理 % 对左上角的网格点进行处理 z=(-h^2*fun(x(1),y(m-1))+gun(a,y(m-1))+r*gun(x(1),d)+r*u(1,m-2)+u(2,m-1))/s; norm=abs(z-u(1,m-1)); u(1,m-1)=z; % 对靠近上边界的除第一点和最后点外网格点进行处理 for i=2:n-2 z=(-h^2*fun(x(i),y(m-1))+r*gun(x(i),d)+r*u(i,m-2)+u(i+1,m-1)+u(i-1,m-1))/s; if abs(u(i,m-1)-z)>norm; norm=abs(u(i,m-1)-z); end u(i,m-1)=z; end % 对右上角的网格点进行处理 z=(-h^2*fun(x(n-1),y(m-1))+gun(b,y(m-1))+r*gun(x(n-1),d)+r*u(n-1,m-2)+u(n-2,m-1))/s; if abs(u(n-1,m-1)-z)>norm norm=abs(u(n-1,m-1)-z); end u(n-1,m-1)=z; % 对不靠近上下边界的网格点进行处理 for j=m-2:-1:2 % 对靠近左边界的网格点进行处理 椭圆方程差分法 1 矩形网上差分方程 考虑二阶椭圆型偏微分方程的第一边值问题 (1.1) ()()()?????=∈=+++--Γy x y x u y x F Eu Du Cu u u y x yy xx ,,,αG 其中C ,E D ,是常数;0≥E ;()()G C 0,∈=y x F F ;(,)x y α是给定的光滑函数。假设(5.1)存在光滑的唯一解。 为简单起见,假设G 是矩形区域,其四个边与相应坐标轴平行。考虑矩形网格:1h 和2h 分别为x 和y 方向的步长,h G 为网格内点节点集合,h Γ为网格边界点集合,=h G h G h Γ。 对于内点()j i y x ,h G ∈用如下的差分方程逼近(1.1) (1.2) 21 ,1,12h u u u j i ij j i -++---221,1,2h u u u j i ij j i -++-+1,1,12h u u C j i j i -+-+21,1,2h u u D j i j i -+-+ij Eu =ij F 其中),(j i ij y x F F =。(1.2)通常称为五点差分格式。 用(1.1)的真解(,)u x y 在网点上的值(,)i j u x y 、1(,)i j u x y -等等分别替换(1.2)中的ij u 、1,i j u -等等,然后在(,)i j x y 点处作Tailor 展开,便知(1.2)逼近(1.1) 的截断误差阶为() 2221h h O +。 方程(1.2)可以改写为 (1.3) j i a ,1-j i u ,1-+j i a ,1+j i u ,1++1,-j i a 1,-j i u +1,+j i a 1,+j i u +j i a ,j i u ,ij F = 对每一内点都可以列出这样一个方程。遇到边界点时,因为边界点u 的函数值已知,将相应的项挪到右端去。最后,得到一个以u 的内点近似值为未知数的线性方程组。这个方程组是稀疏的,并且当1h 和2h 足够小时是对角占优的。 可以证明,五点差分格式关于右端和初值都是稳定的,收敛阶为2212()O h h +。 用五点有限差分格式求解椭圆型方程(偏微分方程)程序3 2010-06-16 06:55 function varargout=liu(varargin) a=0;b=2;c=0;d=1;h1=1/32;h2=1/32; x=a:h1:b; y=c:h2:d; m=length(x); n=length(y); C=tri1(-1/h1^2,2*(1/h1^2+1/h2^2),-1/h1^2,n-2); D=-1/h1^2*eye(n-2); AA=tri2(D,C,D,m-2); BB=fc1t(a,b,c,d,h1,h2); XX=AA\BB; UU=zeros(m,n); for r=1:m for j=1:n UU(r,j)=fU(x(r),y(j)); end end UL=UU; for r=2:m-1 UL(r,2:n-1)=XX((r-2)*(n-2)+1:(r-1)*(n-2)); end [Y,X]=meshgrid(y,x); Z=abs(UL-UU); mesh(Y,X,Z); shading flat; xlabel('X','FontSize',14); ylabel('Y','FontSize',14); zlabel('error','FontSize',14); title('误差图') %求解下问题 %-(u_xx+u_yy)=f(x,y) x,y 在区域内x in a 第4章 椭圆型方程的有限差分法 §2 一维差分格式 1、用积分插值法导出逼近微分方程的差分格式。 d du du Lu=-(p )+r +qu=f,a j. 椭圆方程数值解法 本章考虑椭圆微分方程数值解法。首先以二维二阶椭圆方程为例,给出矩形网和三角网上的差分法。然后以一维二阶椭圆方程为例,简要描述有限元法的基本思想。 J.1 矩形网上差分方程 考虑二维区域(区域=连通的开集)G 上的二阶椭圆型偏微分方程第一边值问题 (j.1) ()()() ,,,xx yy x y u u Cu Du Eu F x y u x y x y αΓ?--+++=∈?? =??G 其中C ,E D ,是常数;0≥E ;()()G C 0,∈=y x F F ;(,)x y α是给定的光滑函数; Γ是G 的边界;G =ΓG 。假设(J.1)存在光滑的唯一解。 考虑一种简单情形,即求解区域G 是矩形区域,并且其四个边与相应坐标轴平行。令1h 和2h 分别为x 和y 方向的步长,用平行于坐标轴的直线段分割区域 G ,构造矩形网格: h G 为网格内点节点集合,h Γ为网格边界节点集合,=h G h G h Γ。 对于内点()j i y x ,h G ∈,用如下的差分方程逼近微分方程(J.1): (J.2) 1,1,,1,1 1,1,,1,1 2 2 212 1 2 2222i j ij i j i j ij i j i j i j i j i j ij ij u u u u u u u u u u C D Eu F h h h h +++-+-+--+-+--- - +++=其中),(j i ij y x F F =。(J.2)通常称为五点差分格式。 方程(J.2)可以整理改写为 (J.3) j i a ,1-j i u ,1-+j i a ,1+j i u ,1++1,-j i a 1,-j i u +1,+j i a 1,+j i u +j i a ,j i u ,ij F = 对每一内点()j i y x ,都可以列出这样一个方程。方程中遇到边界点时,注意到边界点上函数值u 已知,将相应的项挪到右端去。最后得到以u 的内点近似值为未知数的线性方程组。这个方程组是稀疏的,并且当1h 和2h 足够小时是对角占优的。 《数值计算方法》实验报告 实验名称:实验1 非线性方程的简单迭代法和Steffensen 迭代法 实验题目:分别用简单迭代法和Steffensen 迭代法求方程 010423=-+x x 在 [1, 2] 内的一个实根. 实验目的:理解并掌握简单迭代法和Steffensen 迭代法 基础理论:简单迭代法和Steffensen 迭代法 1).简单迭代法的原理:将一元非线性方程:0)(=x f 改写成等价方程:)(x x ρ= ,对此,从某个初始值x0开始,对应式)(x x ρ= 构成迭代公式 ,...1,0),(1==+k x x k k ρ ,这样就可以确定序列 {}k x (k=0,1,2…)。如果 {}k x 有极限 *lim x x k k =∞→ ,由式 ,...1,0),(1==+k x x k k ρ 两边取极限可得 )(**x x ρ= ,可知 * x 为方程0)(=x f 的近似解。 2)Steffensen 迭代法的原理: 通过把改进的Aitken 方法应用于根据不动点迭代所得到的线性收敛序列,将收敛速度加速到二阶。 ()???? ?????+---===+k k k k k k k k k k k x y z x y x x y z x y 2) ()(21ρρ []x x x x x x x +---=)(2)(()()(2ρρρρψ 实验环境:操作系统:Windows 7; 实验平台:Turbo C++ 实验过程:写出算法→编写程序→调试运行程序→计算结果 1)简单迭代法的算法: Input:初始近似值x0,精度要求del,最大迭代次数N Output:近似解x 或失败信息 1. n ←1 2. While n ≤N do; 3. x ←f(x0); 4. if | x-x0| 用五点有限差分格式求解椭圆型方程(偏微分方程) 2010-04-20 22:31 function varargout=liu(varargin) a=0;b=2;c=0;d=1;h1=1/16;h2=1/16; f=inline('(pi^2-1)*exp(x)*sin(pi*y)','x','y'); g1x=inline('0'); g2x=inline('0'); g1y=inline('sin(pi*y)'); g2y=inline('exp(2)*sin(pi*y)'); [X,Y,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2); mesh(X,Y,Z); shading flat; xlabel('X','FontSize',14); ylabel('Y','FontSize',14); zlabel('error','FontSize',14); title('误差图'); function [X,Y,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2) %求解下问题 %-(u_xx+u_yy)=f(x,y) x,y 在区域内x in a %h2离散y方向的步长 N=10000; x=a:h1:b; y=c:h2:d; m=length(x); n=length(y); ee=0.0001; [Y,X]=meshgrid(y,x); Z=zeros(m,n); U=zeros(m,n); for i=2:m-1 U(i,1)=feval(g1x,x(i)); U(i,n)=feval(g2x,x(i)); end for j=1:n U(1,j)=feval(g1y,y(j)); U(m,j)=feval(g2y,y(j)); end %while true %下为雅克比迭代法 %---------------------------------------------------------------------- for k=1:N 实验报告 实验项目名称椭圆型偏微分方程 实验室数学实验室 所属课程名称微分方程数值方法 实验类型算法设计 实验日期2014年6月6日 班级 学号 姓名 成绩 实验概述: 【实验目的及要求】 实验目的是通过分析Possion问题并用交替迭代法来求解其次边值问题,进一步了解交替迭代法的算法特点——即在矩形区域上的差分格式可以大大降低计算量。实验要求是利用Peaceman-Rachford迭代格式编写出相应的代 码解决Possion问题。 【实验原理】 对于简单的椭圆型偏微分方程 Poission 方程: 采用正方形网格剖分正方形区域Ω ,对 x 和 y 方向采用中心差分并记则对Poission方程离散后差分格式可写成; 改写为 由此得Peaceman-Rachford 迭代格式为 其分量形式为 将以上两步写成矩阵形式,第一步迭代为: 第二步迭代为: 这里的 gij 和 gij 分别为 迭代参数可取为: 实际上每个迭代步相当于解N ?1个系数矩阵为三对角阵的N ?1阶线性代数方程组,可用追赶法求解。 【实验环境】(使用的软硬件) 软件: MATLAB 2012a 硬件: 电脑型号:联想 Lenovo 昭阳E46A笔记本电脑 操作系统:Windows 8 专业版 处理器:Intel(R)Core(TM)i3 CPU M 350 @2.27GHz 2.27GHz 实验内容: 【实验方案设计】 利用Peaceman-Rachford迭代格式求解 求解域Ω : 0 ≤ x, y ≤ 1,其精确解为u = sin πx sin πy。 首先利用上述原理进行分析,从而利用Matlab软件编写出相应程序。 【实验过程】(实验步骤、记录、数据、分析) 我们首先编写一个m文件,包含交替方向迭代法程序如下: function u=alter(a0,b0,f,h) %输入-a0为x,y方向起始端点; %-b0为x,y方向终点; %-f为方程右端函数; %-h为网格步长; %输出-u为解矩阵。 p=200; N=fix((b0-a0)/h); u=zeros(N+1); v=zeros(N+1); g=zeros(N+1); x=a0:h:b0; y=x; tau=h*h/(2*sin(pi*h)); a=-tau*ones(1,N-2); c=a; d=(h*h+2*tau)*ones(1,N-1); for k=1:p err=0; for i=2:N for j=2:N g(i,j)=(h*h-2*tau)*u(i,j)+tau*(u(i,j+1)+u(i,j-1)+h*h*f(x(i),y(j))); end 第9章 偏微分方程的差分方法 含有偏导数的微分方程称为偏微分方程。由于变量的增多和区域的复杂性,求偏微分方程的精确解一般是不可能的,经常采用数值方法求方程的近似解。偏微分方程的数值方法种类较多,最常用的方法是差分方法。差分方法具有格式简单,程序易于实现,计算量小等优点,特别适合于规则区域上偏微分方程的近似求解。本章将以一些典型的偏微分方程为例,介绍差分方法的基本原理和具体实现方法。 9.1椭圆型方程边值问题的差分方法 9.1.1 差分方程的建立 最典型的椭圆型方程是Poisson (泊松)方程 G y x y x f y u x u u ∈=??+??-≡?-),(),,()(2222 (9.1) G 是x ,y 平面上的有界区域,其边界Γ为分段光滑的闭曲线。当f (x ,y )≡0时,方程 (9.1)称为Laplace(拉普拉斯)方程。椭圆型方程的定解条件主要有如下三种边界条件 第一边值条件 ),(y x u α=Γ (9.2) 第二边值条件 ),(y x n u β=??Γ (9.3) 第三边值条件 ),()( y x ku n u γ=+??Γ (9.4) 这里,n 表示Γ上单位外法向,α(x,y ),β(x,y ),γ(x,y )和k (x,y )都是已知的函数,k (x,y )≥0。满足方程(9.1)和上述三种边值条件之一的光滑函数u (x ,y )称为椭圆型方程边值问题的解。 用差分方法求解偏微分方程,就是要求出精确解u (x ,y )在区域G 的一些离散节点(x i ,y i )上的近似值u i ,j ≈(x i ,y i )。差分方法的基本思想是,对求解区域G 做网格剖分,将偏微分方程在网格节点上离散化,导出精确解在网格节点上近似值所满足的差分方程,最终通过求解差分方程,通常为一个线性方程组,得到精确解在离散节点上的近似值。 设G ={0 170 第9章 偏微分方程的差分方法 含有偏导数的微分方程称为偏微分方程。由于变量的增多和区域的复杂性,求偏微分方程的精确解一般是不可能的,经常采用数值方法求方程的近似解。偏微分方程的数值方法种类较多,最常用的方法是差分方法。差分方法具有格式简单,程序易于实现,计算量小等优点,特别适合于规则区域上偏微分方程的近似求解。本章将以一些典型的偏微分方程为例,介绍差分方法的基本原理和具体实现方法。 9.1椭圆型方程边值问题的差分方法 9.1.1 差分方程的建立 最典型的椭圆型方程是Poisson (泊松)方程 G y x y x f y u x u u ∈=??+??-≡?-),(),,()(2222 (9.1) G 是x ,y 平面上的有界区域,其边界Γ为分段光滑的闭曲线。当f (x ,y )≡0时,方程 (9.1)称为Laplace(拉普拉斯)方程。椭圆型方程的定解条件主要有如下三种边界条件 第一边值条件 ),(y x u α=Γ (9.2) 第二边值条件 ),(y x n u β=??Γ (9.3) 第三边值条件 ),()( y x ku n u γ=+??Γ (9.4) 这里,n 表示Γ上单位外法向,α(x,y ),β(x,y ),γ(x,y )和k (x,y )都是已知的函数,k (x,y )≥0。满足方程(9.1)和上述三种边值条件之一的光滑函数u (x ,y )称为椭圆型方程边值问题的解。 用差分方法求解偏微分方程,就是要求出精确解u (x ,y )在区域G 的一些离散节点(x i ,y i )上的近似值u i ,j ≈(x i ,y i )。差分方法的基本思想是,对求解区域G 做网格剖分,将偏微分方程在网格节点上离散化,导出精确解在网格节点上近似值所满足的差分方程,最终通过求解差分方程,通常为一个线性方程组,得到精确解在离散节点上的近似值。 设G ={0 山西大学计算机与信息技术学院 实验报告 姓名学号专业班级 课程名称计算方法实验实验日期 成绩指导老师批改日期 实验名称实验三解线性方程组的迭代法 一、实验目的: 用雅可比和高斯—赛德尔迭代法解线性方程组A x=b,式中A为非奇异实矩阵。在给定迭代初值的情况下,进行迭代,直到满足精度要求。 二、实验方法 (1)雅可比迭代法设系数矩阵A为非奇异矩阵,且a ij0≠ ,(i=1,2,3,......,n),从第i个方程中解出 x i , 得其等价形式: ) ( 1 ,1 x a a x i n i j j ij ii i b∑ ≠ = - = ,取初始向量 ) ,...., , , ()0( )0( 3 )0( 2 )0( 1 )0(x x x x x n = ,可建立相应的 迭代公式: ) ( 1)( ,1 )1 (b x a a x i k j n i j j ij ij k i + - =∑ ≠ = + (2)高斯—赛德尔迭代法 每计算出一个新的分量便立即用它取代对应的旧分量进行迭代,可能收敛更快,据此思想课构造高斯 —赛德尔迭代法,其迭代公式为 ) ,...., 2,0 (), ( 11 11 ) ( )1 ( )1 (n i b x a x a a x j i j n i j k j ij k j ij ij k i = + - - =∑∑ - =+ = + + 三、实验内容 求使|| x x k k) ( )1 (- + ||20001 .0 ≤的近视解及相应的迭代次数。初值选为向量b。 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? - - = ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? - - - - - - - - - - - - - - - - 6 2 5 2 5 4 1 1 1 4 1 1 1 4 1 1 1 1 4 1 1 1 4 1 1 1 4 6 5 4 3 2 1 x x x x x x 四、实验程序 雅可比迭代法代码:#include"stdio.h" #include"math.h" #define n 6 #define Nmax 100 用差分法解椭圆型偏微分方程 -(Uxx+Uyy)=(pi*pi-1)e^xsin(pi*y) 0 用差分法解椭圆型偏微分方程 U(0,y)=si n(pi*y),U(2,y)=eA2si n( pi*y); 先自己去看一下关于五点差分法的理论书籍 Matlab 程序: unction [p e u x y k]=wudianchafenfa(h,m,n,kmax,ep) % g-s 迭代法解五点差分法问题 %kmax 为最大迭代次数 %m,n 为x,y 方向的网格数,例如(2-0 ) /0.01=200; %e 为误差,p 为精确解 syms temp ; u=zeros(n+1,m+1); x=0+(0:m)*h; y=0+(0:n)*h; for (i=1:n+1) u(i,1)=sin(pi*y(i)); u(i,m+1)=exp(1)*exp(1)*sin(pi*y(i)); end for (i=1:n) for ( j=1:m) f(i,j)=(pi*pi-1)*exp(x(j))*sin(pi*y(i)); end -(Uxx+Uyy)=(pi*pi-1)eAxsin(pi*y) 0 end t=zeros(n-1,m-1); for (k=1:kmax) for (i=2:n) for ( j=2:m) temp=h*h*f(i,j)/4+(u(i,j+1)+u(i,j-1)+u(i+1,j)+u(i- 1,j))/4; t(i,j)=(temp-u(i,j))*(temp-u(i,j)); u(i,j)=temp; end end t(i,j)=sqrt(t(i,j)); if (k>kmax) break ; end if (max(max(t)) 2015 年秋季学期研究生课程考核 (读书报告、研究报告) 考核科目:偏微分方程数值解法 学生所在院(系):理学院数学系 学生所在学科:数学 学生姓名:H i t e r 学号:1X S012000 学生类别: 考核结果阅卷人 抛物型方程有限差分方法的应用 摘要 抛物型偏微分方程是一类比较重要的偏微分方程。热传导方程是最简单的一种抛物型方程。热传导方程研究的是热传导过程的一个简单数学模型。根据热量守恒定律和傅里叶热传导实验定律可以导出热传导方程。在本篇论文中,将先详述抛物型偏微分方程的有限差分法的相关知识,然后给出抛物型方程的两个具体的应用实例。 关键字:抛物型方程,差分格式,应用 Abstract Parabolic partial differential equation is a kind of important partial differential equation. The heat conduction equation is one of the simplest parabolic equations. The heat conduction equation is a simple mathematical model of the heat conduction process. Heat conduction equation is derived based on the law of conservation of heat and Friyege's law of conduction. In this thesis, we first give a detailed knowledge of the finite difference method for parabolic partial differential equations, and then give two specific examples of the application of the parabolic equation. Keywords: parabolic equation, difference scheme, application 0 前言 抛物型方程是偏微分方程中的三大方程(另两种为双曲型方程和椭圆型方程)之一,如何去研究抛物型方程的性质在《偏微分方程数值解法》的课程中占有很大的比例。如果要研究抛物型方程,我们一般从以下几个方面来研究,分别是:定界问题、格林函数、极值原理、解的正则性、抛物方程、拟线性蜕化和反应扩散方程。但是由于所学知识有限,所以我们在此只简单的介绍抛物型方程的有限差分法并给出两个应用实例。 1 抛物型方程有限差分法 1.1 简单差分法 考虑一维模型热传导方程 )(22x f x u a t u +??=??,T t ≤<0 (1.1) 其中a 为常数。)(x f 是给定的连续函数。(1.1)的定解问题分两类: 第一,初值问题(Cauchy 问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初始条件: ()()x x u ?=0,,∞<<∞-x (1.2) 第二,初边值问题(也称混合问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初Matlab PDE工具箱有限元法求解偏微分方程
用五点有限差分格式求解椭圆型方程(偏微分方程) 程序2
课程名称(中文)偏微分方程数值解专题
椭圆型方程的有限元法
有限差分法的Matlab程序(椭圆型方程)
大连理工大学 高等数值分析 椭圆方程差分法
用五点有限差分格式求解椭圆型方程(偏微分方程) 程序3
椭圆型方程的有限差分法
椭圆方程数值解
非线性方程的简单迭代法和Steffensen迭代法
用五点有限差分格式求解椭圆型方程(偏微分方程)
椭圆型偏微分方程实验报告
第九章-偏微分方程差分方法汇总
第九章 偏微分方程差分方法汇总
计算方法实验三 解线性方程组的迭代法
五点差分法解椭圆型偏微分方程
五点差分法(matlab)解椭圆型偏微分方程
抛物型方程有限差分方法的应用-报告概论
