实用文库汇编之初三数学九上九下压轴题难题提高题培优题(含答案解析)

*作者：角狂风*

作品编号：1547510232155GZ579202

创作日期：2020年12月20日

实用文库汇编之初三数学九上压轴题难题提高题培优

题

一．解答题（共8小题）

1．如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣3，0）、B（1，0）、C（﹣2，1），交y轴于点M．

（1）求抛物线的表达式；

（2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值，并求此时点D的坐标；（3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似（不包括全等）？若存在，求点P的坐标；若不存在，请说明理由．

2．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a ＞0）经过点A和x轴正半轴上的点B，AO=OB=4，∠AOB=120°．（1）求这条抛物线的表达式；

（2）联结OM，求∠AOM的大小；

（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．

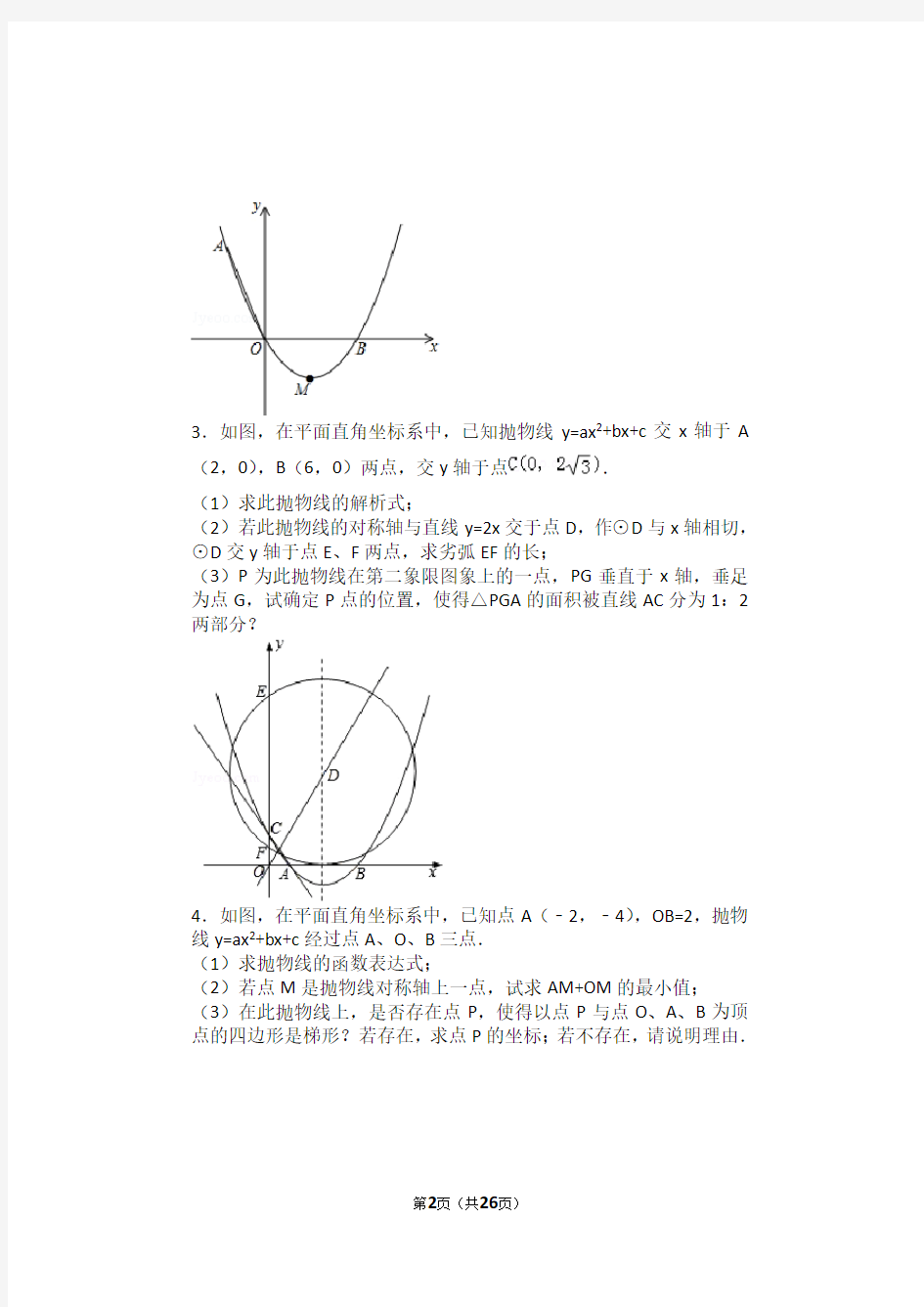
3．如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c交x轴于A （2，0），B（6，0）两点，交y轴于点．

（1）求此抛物线的解析式；

（2）若此抛物线的对称轴与直线y=2x交于点D，作⊙D与x轴相切，⊙D交y轴于点E、F两点，求劣弧EF的长；

（3）P为此抛物线在第二象限图象上的一点，PG垂直于x轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1：2两部分？

4．如图，在平面直角坐标系中，已知点A（﹣2，﹣4），OB=2，抛物线y=ax2+bx+c经过点A、O、B三点．

（1）求抛物线的函数表达式；

（2）若点M是抛物线对称轴上一点，试求AM+OM的最小值；（3）在此抛物线上，是否存在点P，使得以点P与点O、A、B为顶点的四边形是梯形？若存在，求点P的坐标；若不存在，请说明理由．

5．已知抛物线y=﹣x2+bx+c经过点A（0，1），B （4，3）．

（1）求抛物线的函数解析式；

（2）求tan∠ABO的值；

（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．

6．如图1，已知抛物线的方程C1：y=﹣（x+2）（x﹣m）（m＞0）与

x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．

（1）若抛物线C1过点M（2，2），求实数m的值；

（2）在（1）的条件下，求△BCE的面积；

（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH+EH 最小，求出点H的坐标；

（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F 为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．

7．如图，已知抛物线y=x2﹣（b+1）x+（b是实数且b＞2）与x

轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C．

（1）点B的坐标为，点C的坐标为（用含b的代数式表示）；

（2）请你探索在第一象限内是否存在点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直角顶点的等腰直角三角形？如果存在，求出点P的坐标；如果不存在，请说明理由；

（3）请你进一步探索在第一象限内是否存在点Q，使得△QCO，△QOA和△QAB中的任意两个三角形均相似（全等可作相似的特殊情况）？如果存在，求出点Q的坐标；如果不存在，请说明理由．

8．如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG 的面积最大？最大值为多少？

（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包

括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

初三数学九上压轴题难题提高题培优题

参考答案与试题解析

一．解答题（共8小题）

1．如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣3，0）、B（1，0）、C（﹣2，1），交y轴于点M．

（1）求抛物线的表达式；

（2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值，并求此时点D的坐标；（3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似（不包括全等）？若存在，求点P的坐标；若不存在，请说明理由．

【解答】解：由题意可知．解得．

∴抛物线的表达式为y=﹣．

（2）将x=0代入抛物线表达式，得y=1．∴点M的坐标为（0，1）．设直线MA的表达式为y=kx+b，则．

解得．

∴直线MA的表达式为y=x+1．

设点D的坐标为（），则点F的坐标为（）．

DF=

=．

当时，DF的最大值为．

此时，即点D的坐标为（）．

（3）存在点P，使得以点P、A、N为顶点的三角形与△MAO相似．设P（m，）．

在Rt△MAO中，AO=3MO，要使两个三角形相似，由题意可知，点P 不可能在第一象限．

①设点P在第二象限时，∵点P不可能在直线MN上，∴只能PN=3AN，∴，即m2+11m+24=0．解得m=﹣3（舍去）或

m=﹣8．又﹣3＜m＜0，故此时满足条件的点不存在．

②当点P在第三象限时，∵点P不可能在直线MA上，∴只能PN=3AN，

∴，即m2+11m+24=0．

解得m=﹣3或m=﹣8．此时点P的坐标为（﹣8，﹣15）．

③当点P在第四象限时，若AN=3PN时，则﹣3，

即m2+m﹣6=0．

解得m=﹣3（舍去）或m=2．

当m=2时，．此时点P的坐标为（2，﹣）．

若PN=3NA，则﹣，即m2﹣7m﹣30=0．

解得m=﹣3（舍去）或m=10，此时点P的坐标为（10，﹣39）．

综上所述，满足条件的点P的坐标为（﹣8，﹣15）、（2，﹣）、（10，

﹣39）．

2．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a ＞0）经过点A和x轴正半轴上的点B，AO=OB=4，∠AOB=120°．（1）求这条抛物线的表达式；

（2）联结OM，求∠AOM的大小；

（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．

【解答】解：（1）如图，过点A作AD⊥y轴于点D，

∵AO=OB=4，

∴B（4，0）．

∵∠AOB=120°，

∴∠AOD=30°，

∴AD=OA=2，OD=OA=2．

∴A（﹣2，2）．

将A（﹣2，2），B（4，0）代入y=ax2+bx，得：作者：角狂风

作品编号：1547510232155GZ579202

创作日期：2020年12月20日

，解得：，

∴这条抛物线的表达式为y=x2﹣x；

（2）过点M作ME⊥x轴于点E，

∵y=x2﹣x=（x﹣2）2﹣，

∴M（2，﹣），即OE=2，EM=．

∴tan∠EOM==．

∴∠EOM=30°．

∴∠AOM=∠AOB+∠EOM=150°．

（3）过点A作AH⊥x轴于点H，

∵AH=2，HB=HO+OB=6，

∴tan∠ABH==．

∴∠ABH=30°，

∵∠AOM=150°，

∴∠OAM＜30°，

∴∠OMA＜30°，

∴点C不可能在点B的左侧，只能在点B的右侧．∴∠ABC=180°﹣∠ABH=150°，

∵∠AOM=150°，

∴∠AOM=∠ABC．

∴△ABC与△AOM相似，有如下两种可能：

①△BAC与∽△OAM，②△BAC与∽△OMA

∵OD=2，ME=，

∴OM=，

∵AH=2，BH=6，

∴AB=4．

①当△BAC与∽△OAM时，

由=得，解得BC=4．

∴C1（8，0）．

②当△BAC与∽△OMA时，

由=得，解得BC=12．

∴C2（16，0）．

综上所述，如果点C在x轴上，且△ABC与△AOM相似，

则点C的坐标为（8，0）或（16，0）．

3．如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c交x轴于A （2，0），B（6，0）两点，交y轴于点．

（1）求此抛物线的解析式；

（2）若此抛物线的对称轴与直线y=2x交于点D，作⊙D与x轴相切，⊙D交y轴于点E、F两点，求劣弧EF的长；

（3）P为此抛物线在第二象限图象上的一点，PG垂直于x轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1：2两部分？

【解答】解：（1）∵抛物线y=ax2+bx+c经过点A（2，0），B（6，0），；

∴，

解得；

∴抛物线的解析式为：；

（2）易知抛物线的对称轴是x=4，

把x=4代入y=2x，得y=8，

∴点D的坐标为（4，8）；

∵⊙D与x轴相切，∴⊙D的半径为8；

连接DE、DF，作DM⊥y轴，垂足为点M；

在Rt△MFD中，FD=8，MD=4，

∴cos∠MDF=；

∴∠MDF=60°，

∴∠EDF=120°；

∴劣弧EF的长为：；

（3）设直线AC的解析式为y=kx+b；

∵直线AC经过点，

∴，

解得；

∴直线AC的解析式为：；

设点，PG交直线AC于N，则点N坐标为，

∵S

△PNA ：S

△GNA

=PN：GN；

∴①若PN：GN=1：2，则PG：GN=3：2，PG=GN；

即=；

解得：m1=﹣3，m2=2（舍去）；

当m=﹣3时，=；

∴此时点P的坐标为；

②若PN：GN=2：1，则PG：GN=3：1，PG=3GN；

即=；

解得：m1=﹣12，m2=2（舍去）；

当m=﹣12时，=；

∴此时点P的坐标为；

综上所述，当点P坐标为或时，△PGA的面积被直线AC分成1：2两部分．

4．如图，在平面直角坐标系中，已知点A（﹣2，﹣4），OB=2，抛物线y=ax2+bx+c经过点A、O、B三点．

（1）求抛物线的函数表达式；

（2）若点M是抛物线对称轴上一点，试求AM+OM的最小值；（3）在此抛物线上，是否存在点P，使得以点P与点O、A、B为顶点的四边形是梯形？若存在，求点P的坐标；若不存在，请说明理由．

【解答】解：（1）由OB=2，可知B（2，0），

将A（﹣2，﹣4），B（2，0），O（0，0）三点坐标代入抛物线y=ax2+bx+c，得

解得：

∴抛物线的函数表达式为．

答：抛物线的函数表达式为．

（2）由，

可得，抛物线的对称轴为直线x=1，

且对称轴x=1是线段OB的垂直平分线，

连接AB交直线x=1于点M，M点即为所求．

∴MO=MB，则MO+MA=MA+MB=AB

作AC⊥x轴，垂足为C，则AC=4，BC=4，∴AB=

∴MO+MA的最小值为．

答：MO+MA的最小值为．

（3）①若OB∥AP，此时点A与点P关于直线x=1对称，

作者：角狂风

作品编号：1547510232155GZ579202

创作日期：2020年12月20日

由A（﹣2，﹣4），得P（4，﹣4），则得梯形OAPB．

②若OA∥BP，

设直线OA的表达式为y=kx，由A（﹣2，﹣4）得，y=2x．

设直线BP的表达式为y=2x+m，由B（2，0）得，0=4+m，即m=﹣4，∴直线BP的表达式为y=2x﹣4

由，解得x1=﹣4，x2=2（不合题意，舍去）

当x=﹣4时，y=﹣12，∴点P（﹣4，﹣12），则得梯形OAPB．

③若AB∥OP，

设直线AB的表达式为y=kx+m，则，

解得，∴AB的表达式为y=x﹣2．

∵AB∥OP，

∴直线OP的表达式为y=x．

由，得x2=0，解得x=0，

（不合题意，舍去），此时点P不存在．

综上所述，存在两点P（4，﹣4）或P（﹣4，﹣12）

使得以点P与点O、A、B为顶点的四边形是梯形．

答：在此抛物线上，存在点P，使得以点P与点O、A、B为顶点的四

边形是梯形，点P的坐标是（4，﹣4）或（﹣4，﹣12）．

5．已知抛物线y=﹣x2+bx+c经过点A（0，1），B （4，3）．

（1）求抛物线的函数解析式；

（2）求tan∠ABO的值；

（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．

【解答】解：（1）∵抛物线y=﹣x2+bx+c经过点A（0，1），B （4，3），

∴，

解得，

所以，抛物线的函数解析式为y=﹣x2+x+1；

（2）如图，过点B作BC⊥x轴于C，过点A作AD⊥OB于D，

∵A（0，1），B （4，3），

∴OA=1，OC=4，BC=3，

根据勾股定理，OB===5，

∵∠OAD+∠AOD=90°，∠AOD+∠BOC=90°，

∴∠OAD=∠BOC，

又∵∠ADO=∠OCB=90°，

∴△AOD∽△OBC，

∴==，

即==，

解得OD=，AD=，

∴BD=OB﹣OD=5﹣=，

∴tan∠ABO===；

（3）设直线AB的解析式为y=kx+b（k≠0，k、b是常数），

则，

解得，

所以，直线AB的解析式为y=x+1，

设点M（a，﹣a2+a+1），N（a，a+1），

则MN=﹣a2+a+1﹣a﹣1=﹣a2+4a，

∵四边形MNCB为平行四边形，

∴MN=BC，

∴﹣a2+4a=3，

整理得，a2﹣4a+3=0，

解得a1=1，a2=3，

∵MN在抛物线对称轴的左侧，抛物线的对称轴为直线x=﹣=，

∴a=1，

∴﹣12+×1+1=，

∴点M的坐标为（1，）．

6．如图1，已知抛物线的方程C1：y=﹣（x+2）（x﹣m）（m＞0）与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．

（1）若抛物线C1过点M（2，2），求实数m的值；

（2）在（1）的条件下，求△BCE的面积；

（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH+EH 最小，求出点H的坐标；

（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F 为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．

【解答】解：（1）将x=2，y=2代入抛物线的解析式得：﹣×4×（2

﹣m）=2，

解得：m=4，

经检验：m=4是分式方程的解．

∴m的值为4．

（2）y=0得：0=﹣（x+2）（x﹣m），解得x=﹣2或x=m，

∴B（﹣2，0），C（m，0）．

由（1）得：m=4，

∴C（4，0）．

将x=0代入得：y=﹣×2×（﹣m）=2，

∴E（0，2）．

∴BC=6，OE=2．

∴S

=BC?OE=×6×2=6．

△BCE

（3）如图1所示：连接EC交抛物线的对称轴于点H，连接BH，设对称轴与x轴的交点为P．

∵x=﹣，

∴抛物线的对称轴是直线x=1．

∴CP=3．

∵点B与点C关于x=1对称，

∴BH=CH．

∴BH+EH=EH+HC．

∴当H落在线段EC上时，BH+EH的值最小．

∵HP∥OE，

∴△PHC∽△EOC．

∴，即．解得HP=．

∴点H的坐标为（1，）．

（4）①如图2，过点B作EC的平行线交抛物线于F，过点F作FF′⊥x

轴于F′．

∵BF∥EC，

∴∠BCE=∠FBC．

∴当，即BC2=CE?BF时，△BCE∽△FBC．

设点F的坐标为（x，﹣（x+2）（x﹣m）），由，得

．

作者：角狂风

作品编号：1547510232155GZ579202

创作日期：2020年12月20日

解得x=m+2．

∴F′（m+2，0）．

∵∠BCE=∠FBC．

∴，得，解得：．

又∵BC2=CE?BF，

∴，整理得：0=16．此方程无解．

②如图3，作∠CBF=45°交抛物线于F，过点F作FF′⊥x轴于F′，