车辆路径问题的数学模型分析研究

数学建模——回归分析

回归分析——20121060025 吕佳琪企业编号生产性固定资产价值(万元)工业总产值(万元) 1318524 29101019 3200638 4409815 5415913 6502928 7314605 812101516 910221219 1012251624 合计65259801 （2）建立直线回归方程; （3）计算估价标准误差; （4）估计生产性固定资产(自变量)为1100万元时总产值(因变量)的可能值。解: (1)画出散点图,观察二变量的相关方向 x=[318 910 200 409 415 502 314 1210 1022 1225]; y=[524 1019 638 815 913 928 605 1516 1219 1624]; plot(x,y,'or') xlabel('生产性固定资产价值(万元)') ylabel('工业总产值(万元)') 由图形可得,二变量的相关方向应为直线 (2)

x=[318 910 200 409 415 502 314 1210 1022 1225]; y=[524 1019 638 815 913 928 605 1516 1219 1624]; X = [ones(size(x))', x']; [b,bint,r,rint,stats] = regress(y',X,0、05); b,bint,stats b = 395、5670 0、8958 bint = 210、4845 580、6495 0、6500 1、1417 stats = 1、0e+004 * 0、0001 0、0071 0、0000 1、6035 上述相关系数r为1,显著性水平为0 Y=395、5670+0、8958*x (3) 计算方法:W=((Y1-y1)^2+……+(Y10-y10)^2)^(1/2)/10 利用SPSS进行回归分析:

数学建模大赛货物运输问题

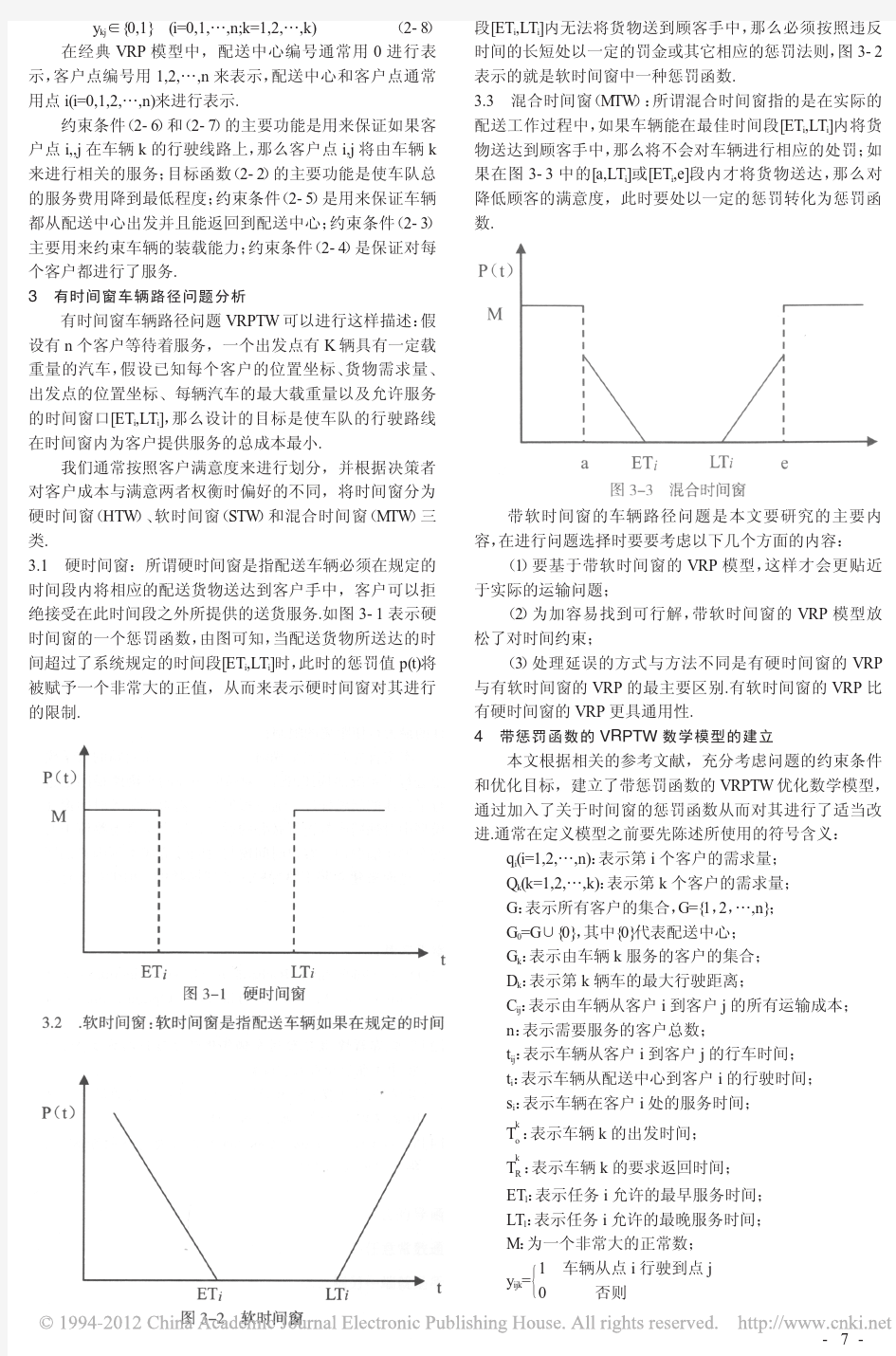
货物配送问题【摘要】本文是针对解决某港口对某地区8个公司所需原材料A、B、C的运输调度问题提出的方案。我们首先考虑在满足各个公司的需求的情况下，所需要的运输的最小运输次数，然后根据卸载顺序的约束以及载重费用尽量小的原则，提出了较为合理的优化模型，求出较为优化的调配方案。针对问题一，我们在两个大的方面进行分析与优化。第一方面是对车次安排的优化分析，得出①~④公司顺时针送货，⑤~⑧公司逆时针送货为最佳方案。第二方面我们根据车载重相对最大化思想使方案分为两个步骤，第一步先是使每个车次满载并运往同一个公司，第二步采用分批次运输的方案，即在第一批次运输中，我们使A材料有优先运输权；在第二批次运输中，我们使B材料有优先运输权；在第三批次中运输剩下所需的货物。最后得出耗时最少、费用最少的方案。耗时为小时，费用为元。针对问题二，加上两个定理及其推论数学模型与问题一几乎相同，只是空载路径不同。我们采取与问题一相同的算法，得出耗时最少，费用最少的方案。耗时为小时，费用为元。针对问题三的第一小问，我们知道货车有4吨、6吨和8吨三种型号。我们经过简单的论证，排除了4吨货车的使用。题目没有规定车子不能变向，所以认为车辆可以掉头。然后我们仍旧采取①~④公司顺时针送货，⑤~⑧公司逆时针送货的方案。最后在满足公司需求量的条件下，采用不同吨位满载运输方案，此方案分为三个步骤：第一，使8吨车次满载并运往同一公司；第二，6吨位车次满载并运往同一公司；第三，剩下的货物若在1~6吨内，则用6吨货车运输，若在7~8吨内用8吨货车运输。最后得出耗时最少、费用最省的方案。耗时为小时，费用为。一、问题重述某地区有8个公司(如图一编号①至⑧)，某天某货运公司要派车将各公司所需的三种原材料A,B,C从某港口(编号⑨)分别运往各个公司。路线是唯一的双向道路(如图１)。货运公司现有一种载重 6吨的运输车，派车有固定成本20元/辆，从港口出车有固定成本为10元/车次(车辆每出动一次为一车次)。每辆车平均需要用15分钟的时间装车，到每个公司卸车时间平均为10分钟，运输车平均速度为60公里／小时(不考虑塞车现象)，每日工作不超过8小时。运输车载重运费元/吨公里，运输车空载费用元/公里。一个单位的原材料A,B,C分别毛重4吨、3吨、1吨，原材料不能拆分，为了安全，大小件同车时必须小件在上，大件在下。卸货时必须先卸小件，而且不允许卸下来的材料再装上车，另外必须要满足各公司当天的需求量(见表１)。问题：

车辆路径问题

车辆路径问题(vehideRoutingProblem，vRP)是组合优化和运筹学领域研究的热点问题之一，其主要研究满足约束条件的最优车辆使用方案以及最优的车辆路径方案。基于基本车辆路径问题的框架，研究满足生产经营和运作需要的各种车辆路径问题，并构建具有高质量和高鲁棒性(roubustuess)的问题求解算法对于提高生产经营管理水平和降低运作成木具有重要的理论意义和现实价值。本文以车辆路径问题为研究对象，综合运用组合优化和现代启发式算法等工具，对几类重要的车辆路径问题模型及其优化算法进行了系统的研究，主要研究工作及成果总结如下: 1.综述了车辆路径问题在定义车辆路径问题分类和扩展标准的基础上，给出了车辆路径问题的研究综述。基于不同的分类标准，首先讨论了主要的标准车辆路径问题扩展问题。在此基础上详细地综述了求解标准车辆路径问题的现代启发式算法，系统地描述了各种算法的实现机理以及各种算法的性能比较结果。 2.综述了求解组合优化问题的现代启发式算法在给出组合优化问题和计算复杂性定义的基础上，综述了求解复杂组合优化问题的各种现代启发式算法。 3.研究了开放式车辆路径问题通过松弛标准车辆路径问题中车辆路线为哈密尔顿巡回(Hamiltoniantour)的假设，研究了车辆路线为哈密尔顿路径(Hamiltonianpath)的开放式车辆路径问题。该问题中车辆在服务完最后一个顾客点后不需要回到车场，若要求回到车场，则必须沿原路返回。在首先给出问题数学模型的基础上，提出了求解开放式车辆路径问题的蚁群优化算法。该算法主体是一个在超立方框架下执行的侧只刃一侧工加尸蚂蚁系统，算法混合了禁忌搜索算法作为局部优化算法，同时集成了一个后优化过程来进一步优化最优解。基于基准测试问题，系统地研究了算法性能。同其它算法的性能比较结果表明本文提出的蚁群优化算法是有效的求解开放式车辆路径问题的方法。 4.研究了带时间窗和带时间期限开放式车辆路径问题通过引入时间约束，研究了两类新的满足时效性要求的开放式车辆路径问题—带时间窗和带时间期限开放式车辆路径问题。首先构建了两类问题的数学模型，同时提出了求解两上海交通大学博十学位论文类问题的基于禁忌搜索的迭代局部搜索算法，该算法集成了不同的解接受标准以及一个基于阂值接受的后优化过程。基于随机产生的测试问题的实验结果表明:基于禁忌搜索的迭代局部搜索算法可以有效地求解带时间窗和带时间期限开放式车辆路径问题。 5.研究了带时间窗和随机旅行时间车辆路径问题通过对标准车辆路径问题的拓展，引入新的边约束条件:时间窗、随机旅行时间和服务时间，研究了一类新的随机车辆路径问题—带时IbJ窗和随机旅行时间车辆路径问题。根据不同的优化标准，分别构建了问题的机会约束规划模型以及带修正随机规划模型。机会约束规划模型是在随机约束以一定的置信水平成立的条件下最小化运输费用。带修正的随机规划模型是一个两阶段优化问题，其确定第一阶段的路线集以最小化第二阶段(随机变量实现后)的期望运输费用。鉴于问题的随机特性，为了有效求解该问题提出了基于随机模拟的禁忌搜索算法。同时基于随机产生的测试问题通过实验检验了算法有效性。 6.研究了固定车辆数异型车辆路径问题在车辆路径问题经典文献中，一般均假设车辆同质目‘车辆数无限。然而在实际运作中，车辆集一般是由具有不同属性(装载能力、固定成本以及单位公里可变费用)的车辆组成，且受运作成本的

#蔬菜运输问题--数学建模

蔬菜运输问题 2012年8月22日摘要本文运用floyd算法求出各蔬菜采购点到每个菜市场的最短运输距离，然后用lingo软件计算蔬菜调运费用及预期短缺损失最小的调运方案，紧接着根据题目要求对算法加以修改得出每个市场短缺率都小于20%的最优调运方案，并求出了最佳的供应改进方案。关键词最短路问题 floyd算法运输问题一、问题重述光明市是一个人口不到15万人的小城市。根据该市的蔬菜种植情况，分别在花市（A），城乡路口（B）和下塘街（C）设三个收购点，再由各收购点分送到全市的8个菜市场，该市道路情况，各路段距离（单位：100m）及各收购点，菜市场①L⑧的具体位置见图1，按常年情况，A,B,C三个收购点每天收购量分别为200，170和160（单位：100 kg）,各菜市场的每天需求量及发生供应短缺时带来的损失（元/100kg）见表 1.设从收购点至各菜市场蔬菜调运费为1元/(100kg.100m). ①7 ② 5 4 8 3 7 A 7 ⑼ 6 B ⑥ 6 8 5 5 4 7 11 7 ⑾ 4 ③ 7 5 6 6 ⑤ 3 ⑿ 5 ④ ⑽ 8 6 6 10 C 10 ⑧ 5 11 ⑦图1 表1 菜市场每天需求（100 kg）短缺损失（元/100kg） ①75 10 ②60 8 ③80 5 ④70 10 ⑤100 10 ⑥55 8 ⑦90 5 ⑧80 8 (a)为该市设计一个从收购点至个菜市场的定点供应方案，使用于蔬菜调运及预

期的短缺损失为最小； (b)若规定各菜市场短缺量一律不超过需求量的20%，重新设计定点供应方案 (c)为满足城市居民的蔬菜供应，光明市的领导规划增加蔬菜种植面积，试问增产的蔬菜每天应分别向A,B,C三个采购点供应多少最经济合理。二、问题分析求总的运费最低，可以先求出各采购点到菜市场的最小运费，由于单位重量运费和距离成正比，题目所给的图1里包含了部分菜市场、中转点以及收购点之间的距离，（a）题可以用求最短路的方法求出各采购点到菜市场的最短路径，乘上单位重量单位距离费用就是单位重量各运输线路的费用，然后用线性方法即可解得相应的最小调运费用及预期短缺损失。第二问规定各菜市场短缺量一律不超过需求量的20%，只需要在上题基础上加上新的限制条件，即可得出新的调运方案。第三问可以在第二问的基础上用灵敏度分析进行求解，也可以建立新的线性问题进行求解。三、模型假设 1、各个菜市场、中转点以及收购点都可以作为中转点； 2、各个菜市场、中转点以及收购点都可以的最大容纳量为610吨； 3、假设只考虑运输费用和短缺费用，不考虑装卸等其它费用； 4、假设运输的蔬菜路途中没有损耗； 5、忽略从种菜场地到收购点的运输费用。四、符号说明 A收购点分送到全市的8个菜市场的供应量分别为a1,b1,c1,d1,e1,f1,g1,h1, B收购点分送到全市的8个菜市场的供应量分别为a2,b2,c2,d2,e2,f2,g2,h2, C收购点分送到全市的8个菜市场的供应量分别为a3,b3,c3,d3,e3,f3,g3,h3, 8个菜市场的短缺损失量分别为a,b,c,d,e,f,g,h(单位均为100kg)。五、模型的建立和求解按照问题的分析，首先就要求解各采购点到菜市场的最短距离，在图论里面关于最短路问题比较常用的是Dijkstra算法，Dijkstra算法提供了从网络图中某一点到其他点的最短距离。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。但由于它遍历计算的节点很多，所以效率较低，实际问题中往往要求网络中任意两点之间的最短路距离。如果仍然采用Dijkstra算法对各点分别计算，就显得很麻烦。所以就可以使用网络各点之间的矩阵计算法，即Floyd 算法。 Floyd算法的基本是：从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。i到j的最短距离不外乎存在经过i和j之间的k和不经过k两种可能，所以可以令k=1，2，3，...，n(n是城市的数目)，在检查d(i,j)和d(i,k)+d(k,j)的值；在此d(i,k)和d(k,j)分别是目前为止所知道的i到k和k到j的最短距离。因此d(i,k)+d(k,j)就是i到j经过k的最短距离。所以，若有d(i,j)>d(i,k)+d(k,j)，就表示从i出发经过k再到j的距离要比原来的i到j距离短，自然把i到j的d(i,j)重写为

配送运输中车辆路径问题研究综述

????????? ?仈?ウ?? ??????????? ?仈а? ?? 亶 ??ウ???а? ???? ?仈? ?? ? ? ?? 学?仈 ??????ウ? ? ? ??? ?? ??????????? ?仈??? ?????? The Current Situation and Development Trends on Vehicle Routing Problems of distribution management Abstract: Vehicle routing problem is one of the attractive research area in the circles of operations research. In this paper, on the basis of introducing briefly the application background, the research classified the vehicle routing problem, analyzed and summarized the progress of different type of problems and solution algorithms. Furthermore, the research progress of the problems is also discussed. It is expected to provide inference for relevant research work. Key words: distribution management; vehicle routing problem; heuristics; overview.

数学建模之回归分析法

什么是回归分析回归分析（regression analysis)是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。运用十分广泛，回归分析按照涉及的自变量的多少，可分为一元回归分析和多元回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。回归分析之一多元线性回归模型案例解析多元线性回归，主要是研究一个因变量与多个自变量之间的相关关系，跟一元回归原理差不多，区别在于影响因素（自变量）更多些而已，例如：一元线性回归方程为：毫无疑问，多元线性回归方程应该为：上图中的x1, x2, xp分别代表“自变量”Xp截止，代表有P个自变量，如果有“N组样本，那么这个多元线性回归，将会组成一个矩阵，如下图所示：那么，多元线性回归方程矩阵形式为：其中：代表随机误差，其中随机误差分为：可解释的误差和不可解释的误差，随机误差必须满足以下四个条件，多元线性方程才有意义（一元线性方程也一样） 1：服成正太分布，即指：随机误差必须是服成正太分别的随机变量。 2：无偏性假设，即指：期望值为0 3：同共方差性假设，即指，所有的随机误差变量方差都相等 4：独立性假设，即指：所有的随机误差变量都相互独立，可以用协方差解释。

今天跟大家一起讨论一下，SPSS---多元线性回归的具体操作过程，下面以教程教程数据为例，分析汽车特征与汽车销售量之间的关系。通过分析汽车特征跟汽车销售量的关系，建立拟合多元线性回归模型。数据如下图所示：（数据可以先用excel建立再通过spss打开）点击“分析”——回归——线性——进入如下图所示的界面：

数学建模运输问题

数学建模运输问题公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]

求量在50个单位以内即可。因此我们在问题二模型的基础上进行改进，以货车容量为限定条件，建立相应的规划模型并设计一个简单的寻路算法，对于模型求解出来的结果，本文利用Kruskal算法结合题中所给的邻接矩阵进行优化。得到优化结果为：第一辆车：-1，第二辆车：，总路程为280公里。关于问题四，在问题一的基础上我们首先用Matlab软件编程确定提货点到每个客户点间的最短路线，然后结合一些限定条件建立一个目标模型，设计一个较好的解决方案进行求解可得到一种很理想的运输方案。根据matlab运行结果分析得出4条最优路线分别为：1-5-2，1-4-3-8，1-7-6，1-9-10。最短总路线为245公里，最小总费用为645。关键词： Floyd算法 Kruskal算法整数规划旅行商问题一、问题重述某运输公司为10个客户配送货物，假定提货点就在客户1所在的位置，从第i个客户到第j个客户的路线距离（单位公里）用下面矩阵中的(,) i j=位置上的数表示（其中∞表示两个客户之间无直接的 i j(,1,,10) 路线到达）。 1、运送员在给第二个客户卸货完成的时候，临时接到新的调度通知，让他先给客户10送货，已知送给客户10的货已在运送员的车上，请帮运送员设计一个到客户10的尽可能短的行使路线（假定上述矩阵中给出了所有可能的路线选择）。 2、现运输公司派了一辆大的货车为这10个客户配送货物，假定这辆货车一次能装满10个客户所需要的全部货物，请问货车从提货点出发给

回归分析在数学建模中的应用

摘要回归分析和方差分析是探究和处理相关关系的两个重要的分支,其中回归分析方法是预测方面最常用的数学方法,它是利用统计数据来确定变量之间的关系,并且依据这种关系来预测未来的发展趋势。本文主要介绍了一元线性回归分析方法和多元线性回归分析方法的一般思想方法和一般步骤,并且用它们来研究和分析我们在生活中常遇到的一些难以用函数形式确定的变量之间的关系。在解决的过程中,建立回归方程,再通过该回归方程进行预测。关键词:多元线性回归分析;参数估计;F检验

回归分析在数学建模中的应用 Abstract Regression analysis and analysis of variance is the inquiry and processing of the correlation between two important branches, wherein the regression analysis method is the most commonly used mathematical prediction method, it is the use of statistical data to determine the relationship between the variables, and based on this relationship predict future trends. introduces a linear regression analysis and multiple linear regression analysis method general way of thinking and the general steps, and use them to research and analysis that we encounter in our life, are difficult to determine as a function relationship between the variables in the solving process, the regression equation is established by the regression equation to predict. Keywords:Multiple linear regression analysis; parameter estimation;inspection II

数学建模运输问题

运输问题摘要本文主要研究的是货物运输的最短路径问题，利用图论中的Floyd算法、Kruskal算法，以及整数规划的方法建立相关问题的模型，通过matlab，lingo 编程求解出最终结果。关于问题一，是一个两客户间最短路程的问题，因此本文利用Floyd算法对其进行分析。考虑到计算的方便性，首先，我们将两客户之间的距离输入到网络权矩阵中；然后，逐步分析出两客户间的最短距离；最后，利用Matlab软件对其进行编程求解，运行得到结果：2-3-8-9-10总路程为85公里。关于问题二，运输公司分别要对10个客户供货，必须访问每个客户，实际上是一个旅行商问题。首先，不考虑送货员返回提货点的情形，本文利用最小生成树问题中的Kruskal算法，结合题中所给的邻接矩阵，很快可以得到回路的最短路线：1-5-7-6-3-4-8-9-10-2；然后利用问题一的Floyd算法编程，能求得从客户2到客户1（提货点）的最短路线是：2-1，路程为50公里。即最短路线为：1-5-7-6-3-4-8-9-10-2-1。但考虑到最小生成树法局限于顶点数较少的情形，不宜进一步推广，因此本文建立以路程最短为目标函数的整数规划模型；最后，利用LINGO软件对其进行编程求解，求解出的回路与Kruskal算法求出的回路一致。关于问题三，是在每个客户所需固定货物量的情况下，使得行程之和最短。这样只要找出两条尽可能短的回路，并保证每条线路客户总需求量在50个单位以内即可。因此我们在问题二模型的基础上进行改进，以货车容量为限定条件，建立相应的规划模型并设计一个简单的寻路算法，对于模型求解出来的结果，本文利用Kruskal算法结合题中所给的邻接矩阵进行优化。得到优化结果为：第一辆车：1-5-2-3-4-8-9-1，第二辆车：1-7-6-9-10-1，总路程为280公里。关于问题四，在问题一的基础上我们首先用Matlab软件编程确定提货点到每个客户点间的最短路线，然后结合一些限定条件建立一个目标模型，设计一个较好的解决方案进行求解可得到一种很理想的运输方案。根据matlab运行结果分析得出4条最优路线分别为：1-5-2，1-4-3-8，1-7-6，1-9-10。最短总路线为245公里，最小总费用为645。关键词： Floyd算法 Kruskal算法整数规划旅行商问题一、问题重述某运输公司为10个客户配送货物，假定提货点就在客户1所在的位置，从第i个客户到第j个客户的路线距离（单位公里）用下面矩阵中的 i j=L位置上的数表示（其中∞表示两个客户之间无直接的路线到i j(,1,,10) (,) 达）。 1、运送员在给第二个客户卸货完成的时候，临时接到新的调度通知，让他先给客户10送货，已知送给客户10的货已在运送员的车上，请帮运送员设计一个到客户10的尽可能短的行使路线（假定上述矩阵中给出了所有可能的路线选择）。 2、现运输公司派了一辆大的货车为这10个客户配送货物，假定这辆货车一次能装满10个客户所需要的全部货物，请问货车从提货点出发给10个客户配送

初中数学几何旋转最值最短路径问题专题训练

初中数学几何旋转最值最短路径问题专题训练专练3 最短路径模型——旋转最值类基本模型图: 【典例1】如图，在矩形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连结B′D，则B′D的最小值是（）． A． B.6 C. D.4 【思路探究】根据E为AB中点，BE＝B′E可知，点A、B、B′在以点E为圆心，AE长为半径的圆上，D、E为定点，B′是动点，当E、B′、D三点共线时，B′D的长最小，此时B′D＝DE－EB′，问题得解. 【解析】∵AE＝BE，BE＝B′E，由圆的定义可知，A、B、B′在以点E为圆心，AB长为直径的圆上，如图所示. B′D的长最小值= DE－EB′.故选A． 22 -=-

【启示】此题属于动点（B′）到一定点（E ）的距离为定值（“定点定长”），联想到以E 为圆心，EB′为半径的定圆，当点D 到圆上的最小距离为点D 到圆心的距离－圆的半径.当然此题也可借助三角形三边关系解决，如，当且仅当点E 、B′、D 三点共线B D DE B E ''≤-时，等号成立. 【典例2】如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE ＝DF ，连接CF 交BD 于点G ，连结BE 交AG 于点H ，若正方形的边长是2，则线段DH 长度的最小值是 . 【思路探究】根据正方形的轴对称性易得∠AHB ＝90°，故点H 在以AB 为直径的圆上.取AB 中点O ，当D 、H 、O 三点共线时，DH 的值最小，此时DH ＝OD －OH ，问题得解. 【解析】由△ABE ≌△DCF ，得∠ABE ＝∠DCF ，根据正方形的轴对称性，可得∠DCF ＝∠DAG ，∠ABE ＝∠DAG ，所以∠AHB ＝90°，故点H 在以AB 为直径的圆弧上.取AB 中点O ，OD 交⊙O 于点H ，此时DH 最小，∵OH ＝， OD ＝，∴DH 的最小值为112 AB =OD －OH . 1【启示】此题属于动点是斜边为定值的直角三角形的直角顶点，联想到直径所对圆周角为直角（定弦定角），故点H 在以AB 为直径的圆上，点D 在圆外，DH 的最小值为DO －OH .当然此题也可利用的基本模型解决. DH OD OH ≤-【针对训练】 1. 如图，在△ABC 中，∠ACB ＝90°，AC ＝2，BC ＝1，点A ，C 分别在x 轴，y 轴上，当点A 在轴正半轴上运动时，点C 随之在轴上运动，在运动过程中，点B 到原点O 的最大x y 距离为（）. A B C ． D ．31

数学建模-回归分析-多元回归分析

1、多元线性回归在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。在实际经济问题中，一个变量往往受到多个变量的影响。例如，家庭消费支出，除了受家庭可支配收入的影响外，还受诸如家庭所有的财富、物价水平、金融机构存款利息等多种因素的影响，表现在线性回归模型中的解释变量有多个。这样的模型被称为多元线性回归模型。（multivariable linear regression model ）多元线性回归模型的一般形式为：其中k 为解释变量的数目，j β (j=1,2,…，k)称为回归系数（regression coefficient)。上式也被称为总体回归函数的随机表达式。它的非随机表达式为： j β也被称为偏回归系数（partial regression coefficient)。 2、多元线性回归计算模型多元性回归模型的参数估计，同一元线性回归方程一样，也是在要求误差平方和（Σe)为最小的前提下，用最小二乘法或最大似然估计法求解参数。设（ 11 x ， 12 x ，…， 1p x ， 1 y ），…，（ 1 n x ， 2 n x ，…， np x ， n y ）是一个样本，用最大似然估计法估计参数：达到最小。

把（4）式化简可得：引入矩阵：方程组（5）可以化简得：可得最大似然估计值：

3、Matlab 多元线性回归的实现多元线性回归在Matlab 中主要实现方法如下：（1）b=regress(Y, X ) 确定回归系数的点估计值其中（2）[b,bint,r,rint,stats]=regress(Y,X,alpha)求回归系数的点估计和区间估计、并检验回归模型 ①bint 表示回归系数的区间估计. ②r 表示残差 ③rint 表示置信区间 ④stats 表示用于检验回归模型的统计量,有三个数值：相关系数r2、F 值、与F 对应的概率p 说明：相关系数r2越接近1，说明回归方程越显著；F>F1-alpha(p,n-p-1) 时拒绝H0，F 越大，说明回归方程越显著；与F 对应的概率p<α 时拒绝H0，回归模型成立。 ⑤alpha 表示显著性水平(缺省时为0.05) （3）rcoplot(r,rint) 画出残差及其置信区间

数学建模--运输问题

数学建模运输问题

华东交通大学数学建模 2012年第一次模拟训练题所属学校：华东交通大学（ECJTU ）参赛队员：胡志远、周少华、蔡汉林、段亚光、李斌、邱小秧、周邓副、孙燕青指导老师：朱旭生（博士）摘要：本文的运输问题是一个比较复杂的问题，大多数问题都集中在最短路径的求解问题上，问题特点是随机性比较强。根据不同建模类型针对问题一，我们直接采用Dijkstra 算法（包括lingo 程序和手算验证），将问题转化为线性规划模型求解得出当运送员在给第二个客户卸货完成的时，若要他先给客户10送货，此时尽可能短的行使路线为：109832V V V V V →→→→，总行程85公里。针对问题二，我们首先利用prim 算法求解得到一棵最小生成树： 121098436751V V V V V V V V V V V →→→→→→→→→→ 再采用Dijkstra 算法求得客户2返回提货点的最短线路为12V V →故可得到一条理想的回路是：121098436751V V V V V V V V V V V →→→→→→→→→→ 后来考虑到模型的推广性，将问题看作是哈密顿回路的问题，建立相应的线性规划模型求解，最终找到一条满足条件的较理想的的货车送货的行车路线： 121098436751V V V V V V V V V V V →→→→→→→→→→。针对问题三，我们首先直接利用问题二得一辆车的最优回路，以货车容量为限定条件，建立相应的规划模型并设计一个简单的寻路算法，最终可为公司确定合理的一号运输方案:两辆车全程总和为295公里（见正文）；然后建立线性规划模型得出二号运输方案：两辆车全程总和为290公里（见正文）；针对问题四，

车辆路径问题研究综述

摘要：作为现代物流领域的研究前沿，车辆路径问题的求解算法及应用领域一直是学者研究的重点。本文在研读大量文献的基础上介绍了遗传算法的研究现状及其应用情况，并对车辆路径优化在生鲜农产品配送上的应用进行了简单的综述。关键词：车辆路径问题；遗传算法；生鲜农场品；研究综述一、引言车辆路径问题最早在60年代被提出，dantzig和ramser首次在交通领域提出该问题就立即引起了社会的广泛关注。发展到现如今，车辆路径问题的应用已经跳出了交通领域，在别的很多领域被使用，如：通讯、工业管理、航空等。二、遗传算法 1.遗传算法简介达尔文的生物进化论自被提出以来就一直被科学家们广泛应用到各个领域。60年代时美国科学家结合进化论，提出了遗传算法。跟大自然中生物优胜劣汰的进化过程类似，遗传算法在计算过程中模拟了自然界各种群由简单到复杂，由低级到高级的进化过程，不断进化种群，直至使种群达到包含最优解或接近最优解的状态。 2.遗传算法研究现状遗传算法作为一种群体随机搜索方法，在车辆路径问题研究中运用很多。很多国内外的研究学者对基础的遗传算法进行了改良，以期达到求解不同约束条件下车辆路径优化问题的目的。通过研究撰写遗传算法的文献发现，研究学者们分别用各种改进遗传算法对车辆路径问题进行了求解，如：免疫遗传算法、小生境遗传算法，以及遗传算法与爬山算法、禁忌搜索算法、蚁群算法相结合的混合算法。将基础的遗传算法与改进的遗传算法进行对比仿真实验，可以发现经过改良的遗传算法，其各方面能力都更优。罗勇等为了求解更优的物流配送路线，就采用了针对性改进的遗传算法。通过研究发现，改良后的算法不仅收敛速度变快，而且全方位寻优的能力也有很大提高。由此可见改进的遗传算法是能更好的处理物流配送路径问题。基础的遗传算法有容易陷入局部最优和早熟的缺点，为了解决这个问题，周艳聪等设计了基于小生境技术的改进遗传算法，还在改进的遗传算法的基础上求解了物流配送路径的优化问题。不仅如此，还通过对物流配送过程的研究，建立了不带时间窗约束的物流配送优化模型。大规模车场的车辆路径问题是车辆路径优化问题中的一个难点，一直是学者们研究的重点。李波等引入了双层模糊聚类方法，针对基础的遗传算法进行了改进，得到了求解该问题的基本框架。通过随机的实验算例证明，所提出的方法是有效可行的。三、车辆路径问题在生鲜农产品配送中的应用对近年来，针对生鲜农产品配送路径问题的研究已经越来越多，人们对绿色食品的质量要求不断提高，是导致该问题备受关注的根本原因。容易腐烂变质，存放不易是大多数生鲜农产品的特点。而在整个销售过程中，生鲜农产品需要经历从农户手中到经销商手中这样一个配送过程，尽可能在配送过程中选择合适的路径，节约时间，保证生鲜农产品的质量，从而保证农户、经销商、消费者的利益就变得越来越重要。为了保证生鲜农产品的质量、安全，生鲜农产品配送过程中的时效性一直是各个学者研究的关注点，大多数相关文献的模型建立都是以配送时间最短和配送成本最低为目标。王红玲等学者的研究考虑了生鲜农产品的特点构建了以生鲜农产品在途时间最短、配送成本最低为优化目标的农产品配送模型，并采用经过改进后的粒子群算法进行求解。由于生鲜农产品的时效性强的特点，对带时间窗的车辆路径问题的研究也相当多。邱荣祖等在分析了农产品的物流配送模式的基础上，建立了有时限的物流配送路径优化模型，并应用gis于禁忌搜索算法集成技术进行求解。文献中还选用了具体的数据进行了实验的验证，进行了初步的应用

最短路径问题的算法分析及建模案例

最短路径问题的算法分析及建模案例一.摘要 (2) 二.网络最短路径问题的基础知识 (3) 2.1有向图 (5) 2.2连通性.............................................................................................. 错误！未定义书签。 2.3割集.................................................................................................. 错误！未定义书签。 2.4最短路问题 (6) 三．最短路径的算法研究............................................................................. 错误！未定义书签。 3.1最短路问题的提出 (6) 3.2 Bellman最短路方程...................................................................... 错误！未定义书签。 3.3 Bellman-Ford算法的基本思想.................................................... 错误！未定义书签。 3.4 Bellman-Ford算法的步骤............................................................ 错误！未定义书签。 3.5实例.................................................................................................. 错误！未定义书签。 3.6 Bellman-FORD算法的建模应用举例............................................ 错误！未定义书签。 3.7 Dijkstra算法的基本思想 (6) 3.8 Dijkstra算法的理论依据 (6) 3.9 Dijkstra算法的计算步骤 (6) 3.10 Dijstre算法的建模应用举例 (7) 3.11 两种算法的分析........................................................................... 错误！未定义书签。 1.Diklstra算法和Bellman-Ford算法思想有很大的区别 ...... 错误！未定义书签。 Bellman-Ford算法在求解过程中，每次循环都要修改所有顶点的权值，也就是说源点到各顶点最短路径长度一直要到Bellman-Ford算法结束才确定下来。错误！未定义书签。 2.Diklstra算法和Bellman-Ford算法的限制.......................... 错误！未定义书签。 3.Bellman-Ford算法的另外一种理解........................................ 错误！未定义书签。 4.Bellman-Ford算法的改进........................................................ 错误！未定义书签。

回归模型的残差分析

回归模型的残差分析山东胡大波判断回归模型的拟合效果是回归分析的重要内容，在回归分析中，通常用残差分析来判断回归模型的拟合效果。下面具体分析残差分析的途径及具体例子。一、残差分析的两种方法 1、差分析的基本方法是由回归方程作出残差图，通过观测残差图，以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当；在残差图中，残差点比较均匀地落在水平区域中，说明选用的模型比较合适，这样的带状区域的宽度越窄，说明模型的拟合精度越高，回归方程的预报精度越高。 2、可以进一步通过相关指数∑∑==--- =n i i n i i i y y y y R 1 2 1 2 ^ 2 )()(1来衡量回归模型的拟合效果，一般规律是2 R 越大，残差平方和就越小，从而回归模型的拟合效果越好。二、典例分析：例1、某运动员训练次数与运动成绩之间的数据关系如下：试预测该运动员训练47次以及55次的成绩。解答：（1）作出该运动员训练次数x 与成绩y 之间的散点图，如图1所示，由散点图可知，它们之间具有线性相关关系。（2）列表计算：由上表可求得875.40,25.39==y x ， 126568 1 2 =∑=i i x ，137318 1 2=∑=i i y ，

131808 1 =∑=i i i y x ，所以∑∑==---= 8 1 2 8 1 )() )((i i i i i x x y y x x β.0415.188 1 2 28 1≈--= ∑∑==i i i i i x x y x y x 00302.0-≈-=x y βα，所以回归直线方程为.00302.00415.1^ -=x y （3）计算相关系数将上述数据代入∑∑∑===---= 8 1 8 1 2 22 2 8 1 ) 8)(8(8i i i i i i i y y x x y x y x r 得992704.0=r ，查表可知 707.005.0=r ，而05.0r r >，故y 与x 之间存在显着的相关关系。（4）残差分析：作残差图如图2，由图可知，残差点比较均匀地分布在水平带状区域中，说明选用的模型比较合适。计算残差的方差得884113.02 =σ ，说明预报的精度较高。（5）计算相关指数2 R 计算相关指数2 R ＝0.9855.说明该运动员的成绩的差异有98.55％是由训练次数引起的。（6）做出预报由上述分析可知，我们可用回归方程 .00302.00415.1^ -=x y 作为该运动员成绩的预报值。将x ＝47和x ＝55分别代入该方程可得y ＝49和y ＝57，故预测运动员训练47次和55次的成绩分别为49和57. 点评：一般地，建立回归模型的基本步骤为：（1）确定研究对象，明确哪个变量是解释变量，哪个变量是预报变量；（2）画出确定好的解释变量和预报变量的散点图，观察它们之间的关系（如是否存在线性关系等）；（3）由经验确定回归方程的类型（如我们观察到数据呈线性关系，则选用线性回归方程y ＝bx ＋a ）；（4）按一定规则估计回归方程中的参数（如最小二乘法）；（5）得出结果后分析残差图是否有异常（个别数据对应残差过大，或残差呈现不随机的规律性等等），若存在异常，则检查数据是否有误，或模型是否合适等。例2、某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关系，随机抽取