(3)函数的对称变换:
a 2 +
b 2
a 2 +
b 2
① y = f (x ) → y = f (-x ) ) 将 y = f (x ) 图像绕 y 轴翻折 180°(整体翻折) (对三角函数来说:图像关于 x 轴对称)
② y = f (x ) → y = - f (x ) 将 y = f (x ) 图像绕 x 轴翻折 180°(整体翻折) (对三角函数来说:图像关于 y 轴对称) ③ y = f (x ) → y = f ( x ) 将 y = f (x ) 图像在 y 轴右侧保留,并把右侧图像绕 y 轴
翻折到左侧(偶函数局部翻折)
④ y = f (x ) → y = f (x ) 保留 y = f (x ) 在 x 轴上方图像, x 轴下方图像绕 x 轴翻折上去(局部翻动)
四、三角恒等变换
1. 两角和与差的正弦、余弦、正切公式: (1)sin(+)= sin cos +sin cos
(2)sin(-
)= sin cos -sin cos
(3) c os(
+ ) = c os cos - s in sin
(4) cos(- ) = cos cos + sin sin
(5)tan(+ )=
(6)tan(
- )= tan + tan ?
1 - tan tan
tan - t an ?
1 + tan tan
tan + t an = tan (+)(1- t an tan
)
tan - tan = tan (-
)(1+ t an
tan
)
(7) a sin +b cos =
a 2 +
b 2 sin(+
) (其中,辅助角所在象限由点(a , b ) 所在的象限
决定,sin
=
b , cos
= a
,tan = b a ,该法也叫合一变形).
(8) 1+tan =
tan(
+) 1- tan = tan( -
)
1- tan 4
1+ tan 4
1 - cos a
21 + cos a
2
2.二倍角公式
(1)sin 2a = 2sin a cos a
(2)cos 2a = cos2 a - sin2 a =1 - 2sin2 a = 2cos2 a -1 tan 2a =
2 tan a
(3)(
3
)
1 - tan
2 a
3.降幂公式:
cos2 a =
1 + cos 2a (1)2
4.升幂公式
(1)1+ cos= 2 cos2
2 (2) sin2 a =1 - cos 2a
2
(2)1- cos= 2 sin 2
2
(3)1± sin= (sin ± cos )2
2 2
(4)1 = sin 2+ cos2
(5)s in = 2sin cos
2 2
5.
半角公式(符号的选择由
2
所在的象限确定)
(1)sin
a
=±,
2(2)
cos
a
=±,
2
(3)tan
a
=±
2
=
sin a
1 + cos a
=
1 - cos a
sin a
6.万能公式:
2tan1- tan2(1)sin= 2 , (2)cos= 2 ,
1+tan2
2
2 t an (3)tan= 2 .
1- tan2
2 1+ tan2
2
7.三角变换:1 - cos a 1 + cos a
三角变换是运算化简过程中运用较多的变换,提高三角变换能力,要学会创设条件,灵活
12 + ( 3)2
a 2 +
b 2 a 2 + b 2
a 2 +
b 2
1 + cos a ) 运用三角公式,掌握运算、化简的方法技能。
(1) 角的变换:角之间的和差、倍半、互补、互余等关系对角变换,还可作添加、
删除角的恒等变形
(2) 函数名称变换:三角变形中常常需要变函数名称为同名函数。采用公式:
a sin +
b cos
= sin(+)其中cos =
a ,sin =
b ,比
y = sin x + 如:
3 cos x
= 12 + ( 3)2 (
1 sin x +
cos x )
1
2( sin x + 2 3 cos x ) 2 = 2(sin x cos
3
+ cos x sin ) = 2 sin(x + )
3 3 (3)注意“凑角”运用:
= (
+
)-
,
= 1
?(+
)- (
-
)? =
- (
-
),
2
3
3
=
12
,则
例如:已知、∈( ), s in(+ )= - , , sin(
-
) 4 cos(+
= ?
4
5
4 13
(4) 常数代换:在三角函数运算、求值、证明中有时候需将常数转化为三角函数,特
别是常数“1”可转化为“ sin 2
+ cos 2”
(5) 幂的变换:对次数较高的三角函数式一般采用降幂处理,有时需要升幂例如:
常用升幂化为有理式。
(6) 公式变形:三角公式是变换的依据,应熟练掌握三角公式的顺用、逆用及变形。 (7) 结构变化:在三角变换中常常对条件、结论的结构进行调整,或重新分组,或移
项,或变乘为除,或求差等等。在形式上有时需要和差与积的互化、分解因式、配方等。
(8) 消元法:如果所要证明的式子中不含已知条件中的某些变量,可用此法
(9) 思路变换:如果一种思路无法再走下去,试着改变自己的思路,通过分析比较去
3 12 + ( 3)2
=
a 2 +
b 2 2 3 3 选择更合适、简捷的方法去解题目。
(10) 利用方程思想解三角函数。如对于以下三个式子: sin a + cos a , sin a cos a
sin a - cos a ,已知其中一个式子的值,其余二式均可求出,且必要时可以换元。
8. 函数的最值(几种常见的函数及其最值的求法):
① y = a sin x + b (或 a cos x + b ) 型:利用三角函数的值域,须注意对字母的讨论 ② y = a sin x + b cos x 型:引进辅助角化成 y = sin(x +
) 再利用有界性
③ y = a sin 2 x + b sin x + c 型:配方后求二次函数的最值,应注意 sin x ≤ 1的约束 ④ y =
a sin x +
b 型:反解出sin x ,化归为 sin x ≤ 1解决
c sin x + d
⑥ y = a (sin x + cos x ) + b sin x ? cos x + c 型:常用到换元法: t = sin x + cos x ,但须注意t 的取值范围: t ≤ 。
9. 三角形中常用的关系:
sin A = sin(B + C ) , cos A = -cos(B + C ) , sin A = cos B + C
,
2 2
sin 2 A = -sin 2(B + C ) ,
cos 2 A = cos 2(B + C )
10. 常见数据: sin15? = cos 75? =
6 - 2
,sin 75? = cos15? = 6 + 2, 4 4
tan15? = 2 - , tan 75? = 2 + ,
教育之通病是教用脑的人不用手,不教用手的人用脑,所以一无所能。教育革命的对策是手脑联盟,结果是手与脑的力量都可以大到不可思议。
“”
“”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
三角函数知识点及题型归纳
三角函数高考题型分类总结 一.求值 1.若4sin ,tan 05 θθ=->,则cos θ= . 2.α是第三象限角,2 1)sin(= -πα,则αcos = )25cos(απ+= 3.若角α的终边经过点(12)P -,,则αcos = tan 2α= 4.下列各式中,值为 2 3 的是 ( ) (A )2sin15cos15?? (B )?-?15sin 15cos 22(C )115sin 22-?(D )?+?15cos 15sin 22 5.若02,sin 3cos απαα≤≤> ,则α的取值范围是: ( ) (A),32ππ?? ??? (B),3ππ?? ??? (C)4,33ππ?? ??? (D)3,32 ππ ?? ??? 二.最值 1.函数()sin cos f x x x =最小值是 。 2.若函数()(13tan )cos f x x x =+,02 x π ≤< ,则()f x 的最大值为 3.函数()cos 22sin f x x x =+的最小值为 最大值为 。 4.已知函数()2sin (0)f x x ωω=>在区间,34ππ?? - ??? ?上的最小值是2-,则ω的最小值等于 5.设02x π?? ∈ ??? ,,则函数22sin 1sin 2x y x +=的最小值为 . 6.将函数x x y cos 3sin -=的图像向右平移了n 个单位,所得图像关于y 轴对称,则n 的最小正值是 A . 6π7 B .3π C .6π D .2 π 7.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1 B .2 C .3 D .2 8.函数2 ()sin 3sin cos f x x x x =+在区间,42ππ?? ? ??? 上的最大值是 ( ) A.1 B. 13 2 + C. 3 2 D.1+3 三.单调性 1.函数]),0[()26 sin(2ππ ∈-=x x y 为增函数的区间是 ( ).
高中文科数学三角函数知识点总结
三角函数知识点 一.考纲要求 考试内容3 要求层次 A B C 三角函数、 三角恒等 变换、 解三角形 三角函数 任意角的概念和弧度制 √ △ 弧度与角度的互化◇ √ 任意角的正弦、余弦、正切的定义 √ 用单位圆中的三角函数线表示正弦、余弦和正切 √ 诱导公式 √ △ 同角三角函数的基本关系式 √ 周期函数的定义、三角函数的周期性 √ 函数sin y x =,cos y x =,tan y x =的图象 和性质 √ 函数sin()y A x ω?=+的图象 √ 用三角函数解决一些简单的实际问题◇ √ 三角 恒等 变换 两角和与差的正弦、余弦、正切公式 √ 二倍角的正弦、余弦、正切公式 √ 简单的恒等变换 √ 解三角形 正弦定理、余弦定理 √ △ 解三角形 √ △ 二.知识点 1.角度制与弧度制的互化:,23600π= ,1800π= 1rad =π 180°≈57.30°=57°18ˊ. 1°= 180 π≈0.01745(rad ) 2.弧长及扇形面积公式 弧长公式:r l .α= 扇形面积公式:S=r l .2 1 α----是圆心角且为弧度制。 r-----是扇形半径 3.任意角的三角函数 设α是一个任意角,它的终边上一点p (x,y ), r=22y x +
(1)正弦sin α= r y 余弦cos α=r x 正切tan α=x y (2)各象限的符号: sin α cos α tan α 4、三角函数线 正弦线:MP; 余弦线:OM; 正切线: AT. 5.同角三角函数的基本关系: (1)平方关系:sin 2α+ cos 2α=1。 (2)商数关系: ααcos sin =tan α(z k k ∈+≠,2 ππ α) 6.诱导公式:奇变偶不变,符号看象限 ()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-. ()5sin cos 2π αα??-= ???,cos sin 2παα?? -= ??? . ()6sin cos 2παα??+= ???,cos sin 2παα??+=- ??? . x y +O — — + x y O — + + — + y O — + + — (3) 若 o|cosx| |cosx|>|sinx| |cosx|>|sinx| |sinx|>|cosx| sinx>cosx cosx>sinx 16. 几个重要结论:O O x y x y T M A O P x y
【全】初中数学 三角函数知识点总结
锐角三角函数 锐角三角函数 锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),(余割csc)都叫做角A的锐角三角函数。 正弦(sin)等于对边比斜边, 余弦(cos)等于邻边比斜边 正切(tan)等于对边比邻边; 余切(cot)等于邻边比对边 正割(sec)等于斜边比邻边 余割(csc)等于斜边比对边 正切与余切互为倒数 互余角的三角函数间的关系。 sin(90°-α)=cosα, cos(90°-α)=sinα, tan(90°-α)=cotα, cot(90°-α)=tanα. 同角三角函数间的关系 平方关系: sin^2(α)+cos^2(α)=1 tan^2(α)+1=sec^2(α) cot^2(α)+1=csc^2(α) ?积的关系: sinα=tanα?cosα cosα=cotα?sinα tanα=sinα?secα cotα=cosα?cscα secα=tanα?cscα cscα=secα?cotα ?倒数关系: tanα?cotα=1 sinα?cscα=1 cosα?secα=1
直角三角形ABC中, 角A的正弦值就等于角A的对边比斜边, 余弦等于角A的邻边比斜边 正切等于对边比邻边, 余切等于邻边比对边 三角函数值 (1)特殊角三角函数值 (2)0°~90°的任意角的三角函数值,查三角函数表。 (3)锐角三角函数值的变化情况 (i)锐角三角函数值都是正值 (ii)当角度在0°~90°间变化时, 正弦值随着角度的增大(或减小)而增大(或减小) 余弦值随着角度的增大(或减小)而减小(或增大) 正切值随着角度的增大(或减小)而增大(或减小) 余切值随着角度的增大(或减小)而减小(或增大) (iii)当角度在0°≤α≤90°间变化时, 0≤sinα≤1, 1≥cosα≥0, 当角度在0°<α<90°间变化时, tanα>0, cotα>0. 特殊的三角函数值 0° 30° 45° 60° 90° 0 1/2 √2/2 √3/2 1 ←sinα 1 √3/ 2 √2/2 1/2 0 ←cosα 0 √3/3 1 √3 None ←tanα None √3 1 √3/3 0 ←cotα 解直角三角形 勾股定理,只适用于直角三角形(外国叫“毕达哥拉斯定理”) a^2+b^2=c^2, 其中a和b分别为直角三角形两直角边,c为斜边。
高一三角函数题型总结
1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法:①画直角三角形 ②利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2. 2. 3. 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-236π)+cos 137π·tan4π -cos 133 π= ;
1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α=8 1,且4π<α<2π ,则cos α-sin α的值为 ( ) 33 (D)± 3 3.) 4. ) 5.) * 6.)
三角函数诱导公式 诱导公式可概括为把 απ ±?k 2 的三角函数值转化成角α的三角函数值。(k 指奇数或者偶数, α相当锐角) 口诀“奇变偶不变,符号看象限。”其中奇偶是指2 π 的奇数倍还是偶数倍,变与不变指函数名称的变化。 公式一:=+)2sin(απk =+)2c o s (απk =+)2t a n (απk
三角函数诱导公式练习题 1.若(),2,5 3 cos παππα<≤= +则()πα2sin --的值是 ( ) A . 53 B . 53- C . 54 D . 5 4 - 2.sin (-6 π 19)的值是( ) A 3 6 )= . 10.α是第四象限角,,则αsin 等于________. 13 12 cos =α
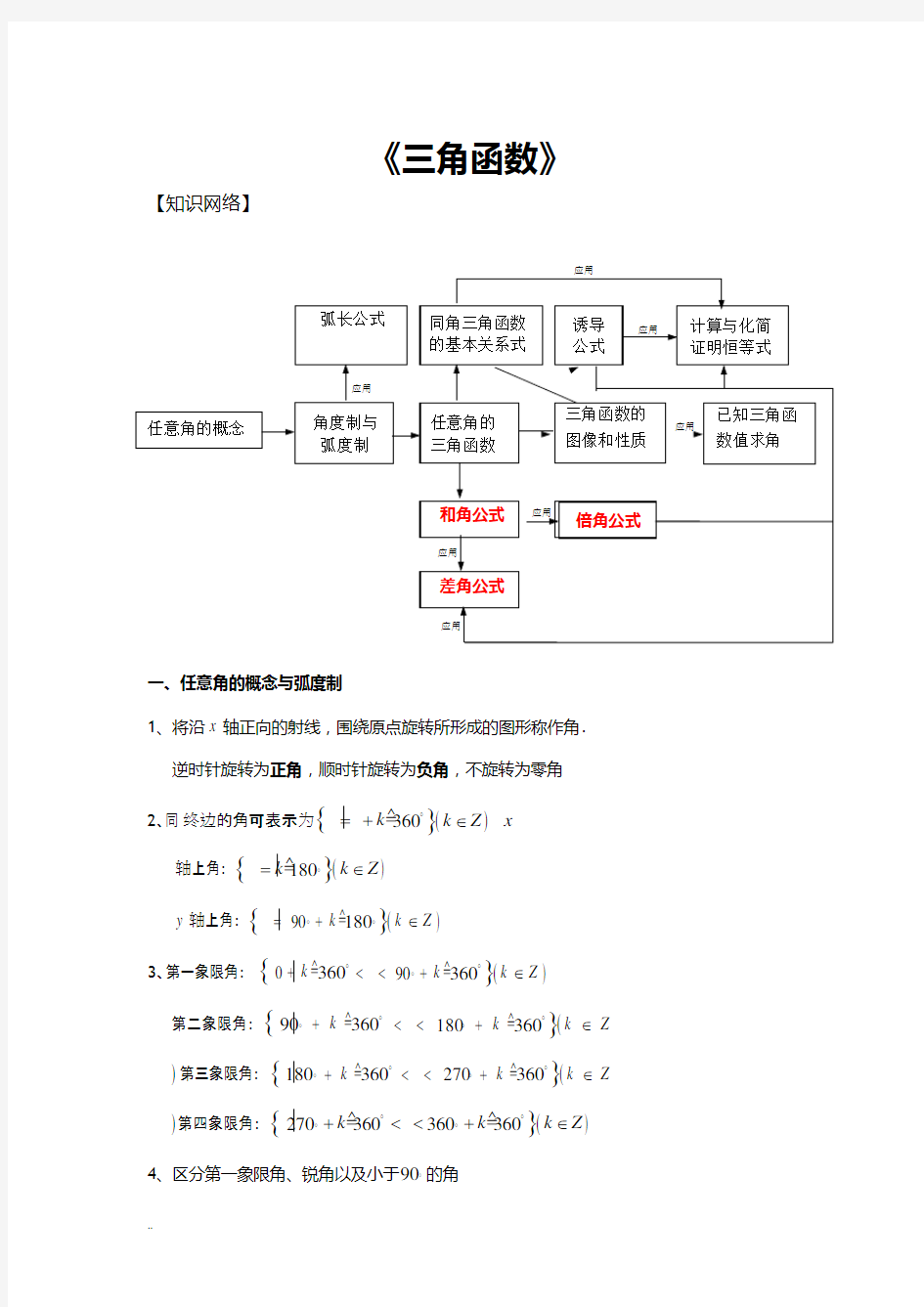
高中数学三角函数知识点归纳总结
《三角函数》 【知识网络】 一、任意角的概念与弧度制 1、将沿x 轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角 2、同终边的角可表示为 {}()360k k Z ααβ? =+∈g x 轴上角:{}()180k k Z αα=∈o g y 轴上角:{}()90180k k Z αα=+∈o o g 3、第一象限角:{}()036090360k k k Z αα? ?+<<+∈o g g 第二象限角:{}()90 360180360k k k Z αα??+<<+∈o o g g 第三象限角:{}()180360270360k k k Z αα? ?+<<+∈o o g g 第四象限角: {}()270 360360360k k k Z αα??+<<+∈o o g g 4、区分第一象限角、锐角以及小于90o 的角 第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈o g g 锐角: {}090αα<,2 4 , 0π απ ≤ ≤=k ,2 345, 1παπ≤≤=k 所以 2 α 在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.0180 1≈=?π 815730.571801'?=?≈? = π 9、弧长与面积计算公式 弧长:l R α=?;面积:211 22 S l R R α=?=?,注意:这里的α均为弧度制. 二、任意角的三角函数 1、正弦:sin y r α=;余弦cos x r α=;正切tan y x α= 其中(),x y 为角α终边上任意点坐标,r = 2、三角函数值对应表: 3、三角函数在各象限中的符号
三角函数知识点汇总
三角函数知识点 考点1、弧度制 1.弧长公式与扇形面积公式: 弧长l r α= ?,扇形面积21 122 S lr r α==扇形(其中r 是圆的半径,α是弧所对圆心角的弧度数). 2.角度制与弧度制的换算: 180π=;180 10.017451()57.305718'180 rad rad rad π π = ≈=≈=; 考点2、任意角的三角函数 1. 定义:在角α上的终边上任取一点(,)P x y ,记22r OP x y ==+ 则sin y r α= , cos x r α=, tan y x α= 2. 三角函数值在各个象限内的符号:(一全二正弦,三切四余弦) 考点3、同角三角函数间的基本关系式 1. 平方关系: 1cos sin 2 2 =+αα 2. 商数关系: α α αcos sin tan =
考点4、诱导公式“奇变偶不变,符号看象限” sin()sin ,cos()cos ,tan()tan .πααπααπαα+=-+=-+= sin()sin ,cos()cos ,tan()tan .αααααα-=--=-=- sin()sin ,cos()cos ,tan()tan . πααπααπαα-=-=--=- sin()cos , 2 cos()sin .2π ααπαα-=-= sin()cos ,2cos()sin .2πααπαα+=+=-3sin()cos ,23cos()sin .2πααπαα-=--=- 3sin()cos , 2 3cos()sin . 2 πααπαα+=-+= 考点5、三角函数的图象和性质 名称 sin y x = cos y x = tan y x = 定义域 x R ∈ x R ∈ {|,}2 x x k k Z π π≠+ ∈ 值 域 [1,1]- [1,1]- (,)-∞+∞ 图象 奇偶性 奇函数 偶函数 奇函数 单 调 性 单调增区间: [2,2]22 k k π π ππ- +(k Z ∈) 单调减区间: 3[2,2]2 2 k k π π ππ+ + k Z ∈) 单调增区间: [2,2]k k πππ-(k Z ∈) 单调减区间: [2,2]k k πππ+(k Z ∈) 单调增区间: (,)22 k k π π ππ- +(k Z ∈) 周期性 2T π= 2T π= T π= 对 称 性 对称中心: (,0)k π,k Z ∈ 对称轴: 2 x k π π=+ ,k Z ∈ 对称中心:(,0)2 k π π+ ,k Z ∈ 对称轴: x k π=, k Z ∈ 对称中心:( ,0)2 k π ,k Z ∈ 对称轴:无 最 值 2,2x k k z π π=+ ∈时,max 1y =; 32,2 x k k z π π=+∈时,min 1y =- 2,x k k z π=∈时,max 1y =; 2,x k k z ππ=+∈,min 1y =- 无 考点6、“五点法”作图
三角函数题型学霸总结(含答案)-
三角函数题型学霸总结(含答案) 阳光老师:祝你学业有成 一、选择题(本大题共30小题,共150.0分) 1.点在函数的图象上,则m等于 A. 0 B. 1 C. D. 2 【答案】C 【解析】 【分析】本题主要考查了正弦函数的性质,属于基础题由题意知,求得m 的值. 【解答】解:由题意知, 所以, 所以. 2.用五点法画,的图象时,下列哪个点不是关键点 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的作法,属于基础题. 熟练掌握五点法作图即可. 【解答】 解:用“五点法”画,的简图时, 横坐标分别为, 纵坐标分别为0,1,0,,0, 故选A. 3.函数y x,x的大致图象是
A. B. C. D. 【答案】B 【解析】 【分析】 本题主要考查三角函数的图像,属于基础题利用“五点法”画出函数图像即可得出答案. 【解答】 解:“五点法”作图: x0 0100 10121 故选B. 4.用“五点法”作出函数的图象,下列点中不属于五点作图中的五个关 键点的是 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的画法以及余弦函数的性质,属于基础题. 分别令,,,,得,3,4,3,2,即可得到五点,再对照选项,即可得到答案. 【解答】 解:,分别令,,,,得,3,4,3,2,
所以五个关键点为,,,,, 可知A不属于. 故选A. 5.已知函数的图象与直线 恰有四个公共点,,,,其中,则 A. B. 0 C. 1 D. 【答案】A 【解析】 【分析】 本题考查了三角函数图象的作法及利用导数求函数图象的切线方程,属于较难题. 由三角函数图象及利用导数求函数图象的切线方程可得:切点坐标为,切线方程为:,又切线过点,则,即,得解. 【解答】 解:由 得 其图象如图所示,
初中三角函数知识点总结(中考复习)
初中三角函数知识点总结(中考复习)
锐角三角函数知识点总结 1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。 2、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4、任意锐角的正切值等于它的余角的余切值;任意锐角的余 A 90 B 90 ∠ - ? = ∠ ? = ∠ + ∠ 得 由B A C
切值等于它的余角的正切值。 5、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 6、正弦、余弦的增减性: 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 7、正切、余切的增减性: 当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。 1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 依据:①边的关系:2 2 2 c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法) 2、应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。 仰角铅垂线 水平线 视线 视线俯角 (2)坡面的铅直高度h 和水平宽度l 的比叫做坡度 (坡比)。用字 母i 表示,即h i l =。坡度一般写成1:m 的形式,如1:5i =等。 把坡面与水平面的夹角记作α(叫做坡角),那么tan h i l α==。 3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。 4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。 反比例函数知识点整理 一、 反比例函数的概念 :i h l =h l α
高中部分三角函数知识点总结
★高中三角函数部分总结 1.任意角的三角函数定义: 设α为任意一个角,点),(y x P 是该角终边上的任意一点(异于原点),),(y x P 到原点的距离为22y x r += ,则: )(tan ),(cos ),(sin y x x y x r x y r y ?=== 正负看正负看正负看ααα 2.特殊角三角函数值: sin30°=1/2 sin45°=√2/2 sin60°=√3/2 cos30°=√3/2 cos45°=√2/2 cos60°=1/2 tan30°=√3/3 tan45°=1 tan60°=√3 cot30°=√3 cot45°=1 cot60°=√3/3 sin15°=(√6-√2)/4 sin75°=(√6+√2)/4 cos15°=(√6+√2)/4 cos75°=(√6-√2)/4(这四个可根据sin (45°±30°)=sin45°cos30°±cos45°sin30°得出) sin18°=(√5-1)/4 (这个值 3.同角三角函数公式: αααααααααα αtan 1 cot ,sin 1csc ,cos 1sec 1cos sin ,cos sin tan 22= ===+= 4.三角函数诱导公式: (1))(;tan )2tan(,cos )2cos( ,sin )2sin(Z k k k k ∈=+=+=+απααπααπα (2);tan )tan(,cos )cos( ,sin )sin(απααπααπα=+-=+-=+ (3);tan )tan(,cos )cos(,sin )sin(αααααα-=-=--=- (函数名称不变,符号看象限)
初中三角函数知识点题型总结+课后练习
锐角三角函数知识点 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4 5、0 锐角三角函数题型训练 类型一:直角三角形求值 1.已知Rt △ABC 中,,12,4 3 tan ,90== ?=∠BC A C 求AC 、AB 和cos B . 2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?= ∠4 3sin AOC 求:AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4.已知A ∠是锐角,17 8 sin = A ,求A cos ,A tan 的值 类型二. 利用角度转化求值:
1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B . 2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,则 tan EFC ∠的值为 ( ) A.34 B.43 C.35 D. 4 5 3. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一点,若1tan 5 DBA ∠= ,则AD 的长为( )A .2 C .1 D .4. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD = 3 16求∠ B 的度数及边B C 、AB 的长. 例2.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,?=3 sin A (1)求AB 边上的高CD ; (2)求△ABC 的面积S ; (3)求tan B . 例3.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5. 求:sin ∠ABC 的值. 对应训练 1.(2012?重庆)如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号) 2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B . 类型四:利用网格构造直角三角形 对应练习: 1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______. 特殊角的三角函数值 例1.求下列各式的值 ?-?+?30cos 245sin 60tan 2=. 计算:3-1+(2π-1)0- 3 3 tan30°-tan45°= 0 30tan 2345sin 60cos 221 ??? ? ???-?+?+= ?-?+?60tan 45sin 230cos 2 tan 45sin 301cos 60?+? -? = B
高一三角函数题型总结
1.已知角围和其中一个角的三角函数值求任意角三角函数值 方法:?画直角三角形 ?利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的?分式 ?齐次式 可以实现αtan 之间的转化 例题:1.已知sin 2cos 5,tan 3sin 5cos αα ααα-=-+那么的值为_____________. 2.已知2tan =α,则1.α αα αcos sin cos sin -+=_____________. 2. α αα α2 2cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.(“1”的代换) 3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法:等式两边完全平方(注意三角函数中判断正负利用角的围进行取舍) 例题:已知πα<∠<0,αsin +αcos =2 1 ,求?αsin .αcos ?αcos -αsin 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-23 6π)+cos 137π·tan4π -cos 133 π= ;
1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)4 3 (D)4 3- 2.已知sin αcos α=8 1,且4π<α<2π ,则cos α-sin α的值为 ( ) (A)2 3 (B)4 3 (C) (D)± 2 3 3.设是第二象限角,则 sin cos αα ( ) (A) 1 (B)tan 2α (C) - tan 2α (D) 1- 4.若tan θ= 3 1,π<θ<3 2π,则sin θ·cos θ的值为 ( ) (A)±3 10 (B) 3 10 5.已知 sin cos 2sin 3cos αααα-+=5 1 ,则tan α的值是 ( ) (A)±83 (B)83 (C)83 - (D)无法确定 * 6.若α是三角形的一个角,且sin α+cos α= 3 2 ,则三角形为 ( ) (A)钝角三角形 (B)锐角三角形 (C)直角三角形 (D)等腰三角形
高中数学三角函数知识点总结(珍藏版)
高中数学三角函数知识点总结 1.特殊角的三角函数值: 2.角度制与弧度制的互化: ,23600π= ,1800 π= 1rad =π 180°≈57.30°=57°18ˊ 1°= 180 π≈0.01745(rad ) 3.弧长及扇形面积公式 (1)弧长公式:r l .α= α----是圆心角且为弧度制 (2)扇形面积公式:S=r l .2 1 r-----是扇形半径 4.任意角的三角函数 设α是一个任意角,它的终边上一点p (x,y ), r=22y x + (1)正弦sin α= r y 余弦cos α=r x 正切tan α=x y (2)各象限的符号: 记忆口诀:一全正,二正弦,三两切,四余弦
sin α cos α tan α 5.同角三角函数的基本关系: (1)平方关系:s in 2α+ cos 2α=1 (2)商数关系:ααcos sin =tan α(z k k ∈+≠,2 ππ α) 6.诱导公式: 记忆口诀:把2 k π α±的三角函数化为α的三角函数,概括为:奇变偶不变,符号看象限。 ()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-. 口诀:函数名称不变,符号看象限. ()5sin cos 2π αα??-= ???,cos sin 2παα?? -= ??? . ()6sin cos 2π αα??+= ???,cos sin 2παα?? +=- ??? . 口诀:正弦与余弦互换,符号看象限. x y O — + + — + y O — + + —
三角函数题型分类总结
专题 三角函数题型分类总结 三角函数公式一览表 ............................................................................................................... 错误!未定义书签。 一 求值问题 ........................................................................................................................................................... - 1 - 练习 ................................................................................................................................................................. - 1 - 二 最值问题 ........................................................................................................................................................... - 2 - 练习 ................................................................................................................................................................. - 3 - 三 单调性问题 ....................................................................................................................................................... - 3 - 练习 ................................................................................................................................................................. - 3 - 四.周期性问题 ........................................................................................................................................................ - 4 - 练习 ................................................................................................................................................................. - 4 - 五 对称性问题 ....................................................................................................................................................... - 5 - 练习 ................................................................................................................................................................. - 5 - 六.图象变换问题 .................................................................................................................................................... - 6 - 练习 ................................................................................................................................................................. - 7 - 七.识图问题 ......................................................................................................................................................... - 7 - 练习 ................................................................................................................................................................. - 9 - 一 求值问题 类型1 知一求二 即已知正余弦、正切中的一个,求另外两个 方法:根据三角函数的定义,注意角所在的范围(象限),确定符号; 例 4 s i n 5 θ=,θ是第二象限角,求cos ,tan θθ 类型2 给值求值 例1 已知2tan =θ,求(1) θ θθθsin cos sin cos -+;(2)θθθθ2 2cos 2cos .sin sin +-的值. 练习 1、sin 330?= tan 690° = o 585sin = 2、(1)α是第四象限角,12 cos 13 α=,则sin α= (2)若4 sin ,tan 05 θθ=- >,则cos θ= . (3)已知△ABC 中,12 cot 5 A =-,则cos A = . (4) α是第三象限角,2 1)sin(=-πα,则αcos = )25cos(απ += 3、(1) 已知5 sin ,5 α= 则44sin cos αα-= .
(推荐)高一三角函数题型总结
题型总结 1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法:画直角三角形 利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的分式 齐次式 可以实现αtan 之间的转化 例题:1.已知 sin 2cos 5,tan 3sin 5cos ααααα -=-+那么的值为_____________. 2.已知2tan =α,则1.α αα αcos sin cos sin -+=_____________. 2.α αα α22cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.(“1”的代换)
3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法:等式两边完全平方(注意三角函数中判断正负利用角的范围进行取舍) 例题:已知πα<∠<0,αsin +αcos =2 1 ,求αsin .αcos αcos -αsin 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-236π)+cos 137π·tan4π -cos 13 3 π= ; 练习题 1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α= 8 1,且4π<α< 2π ,则cos α-sin α的值为 ( ) (A) 2 3 (B)4 3 (C)3 (D)± 2 3
高一三角函数知识点梳理总结
高一三角函数知识 §1.1任意角和弧度制 ?? ? ??零角负角:顺时针防线旋转正角:逆时针方向旋转 任意角..1 2.象限角:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 3.. ①与α(0°≤α<360°)终边相同的角的集合:{} Z k k ∈+?=,360|αββ ②终边在x 轴上的角的集合: {} Z k k ∈?=,180| ββ ③终边在y 轴上的角的集合:{} Z k k ∈+?=,90180| ββ ④终边在坐标轴上的角的集合:{} Z k k ∈?=,90| ββ ⑤终边在y =x 轴上的角的集合:{ } Z k k ∈+?=,45180| ββ ⑥终边在x y -=轴上的角的集合:{} Z k k ∈-?=,45180| ββ ⑦若角α与角β的终边关于x 轴对称,则角α与角β的关系:Z k k ∈-=,βα 360 ⑧若角α与角β的终边关于y 轴对称,则α与角β的关系:Z k k ∈-+=,βα 180360 ⑨若角α与角β的终边在一条直线上,则α与角β的关系:Z k k ∈+=,βα 180 ⑩角α与角β的终边互相垂直,则α与角β的关系:Z k k ∈++=, 90180βα 4. 弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。360度=2π弧度。若圆心角所对 的弧长为l ,则其弧度数的绝对值|r l = α,其中r 是圆的半径。 5. 弧度与角度互换公式: 1rad =(π 180)°≈57.30° 1°=180 π 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. 6.. 第一象限的角:? ?? ? ??∈+< 三角函数知识点汇总
1三角函数的概念 【知识网络】 【考点梳理】 考点一、角的概念与推广 1.任意角的概念:正角、负角、零角 2.象限角与轴线角: 与α终边相同的角的集合:},2|{Z k k ∈+=απββ 第一象限角的集合:{|22,}2 k k k Z π βπβπ<<+∈ 第二象限角的集合:{| 22,}2 k k k Z π βπβππ+<<+∈ 第三象限角的集合:3{|22,}2 k k k Z π βππβπ+<<+∈ 第四象限角的集合:3{| 222,}2 k k k Z π βπβππ+<<+∈ 终边在x 轴上的角的集合:{|,}k k Z ββπ=∈ 终边在y 轴上的角的集合:{|,}2 k k Z π ββπ=+∈ 终边在坐标轴上的角的集合:{|,}2 k k Z π ββ=∈ 要点诠释: 要熟悉任意角的概念,要注意角的集合表现形式不是唯一的,终边相同的角不一定相等,但相等的角终边一定相同,还要注意区间角与象限角及轴线角的区别与联系. 三角函数的概念 角的概念的推广、弧度制 正弦、余弦的诱导公式 同角三角函数的基本关系式 任意角的三角函数
考点二、弧度制 1.弧长公式与扇形面积公式: 弧长l r α= ?,扇形面积21 122 S lr r α==扇形(其中r 是圆的半径,α是弧所对圆心角的弧度数). 2.角度制与弧度制的换算: 180π=o ;18010.017451()57.305718'180 rad rad rad π π = ≈=≈=o o o o ; 要点诠释: 要熟悉弧度制与角度制的互化以及在弧度制下的有关公式. 考点三、任意角的三角函数 1. 定义:在角α上的终边上任取一点(,)P x y ,记r OP ==则sin y r α= , cos x r α=, tan y x α=,cot x y α=,sec r x α=,csc r y α= 2. 三角函数线:如图,单位圆中的有向线段MP ,OM ,AT 分别叫做α的正弦线,余弦线,正切线. 3. 三角函数的定义域:sin y α=,cos y α=的定义域是R α∈;tan y α=,sec y α=的定义域是 {|,}2 k k Z π ααπ≠+ ∈;cot y α=,csc y α=的定义域是{|,}k k Z ααπ≠∈. 4. 三角函数值在各个象限内的符号: 考点四、同角三角函数间的基本关系式 1. 平方关系:2 2 2222sin cos 1;sec 1tan ;csc 1cot α+α=α=+αα=+α. 2. 商数关系:sin cos tan ;cot cos sin α α α= α= α α . 3. 倒数关系:tan cot 1;sin csc 1;cos sec 1α?α=αα=α?α= 要点诠释: ①同角三角函数的基本关系主要用于:(1)已知某一角的三角函数,求其它各三角函数值;(2)证明三角恒等式;(3)化简三角函数式. ②三角变换中要注意“1”的妙用,解决某些问题若用“1”代换,如2 2 1sin cos =α+α, 221sec tan tan 45=α-α==o L ,则可以事半功倍;同时三角变换中还要注意使用“化弦法”、消去法 及方程思想的运用. 考点五、诱导公式 1.2(),,,2k k Z πααπαπα+∈-±-的三角函数值等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值所在象限的符号.
三角函数总结经典例题
第三章 三角函数 3.1任意角三角函数 一、知识导学 1.角:角可以看成由一条射线绕着端点从一个位置旋转到另一个位置所形成的几何图形.角的三要素是:顶点、始边、终边.角可以任意大小,按旋转的方向分类有正角、负角、零角. 2.弧度制:任一已知角α的弧度数的绝对值r l = α,其中l 是以α作为圆心角时所对圆弧的长,r 为圆的半径.规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.用“弧度”做单位来度量角的制度叫做弧度制. 3.弧度与角度的换算:rad π2360=ο ;rad 1745.01801≈=π ο ;1ο ο 30.57180≈?? ? ??=πrad .用弧度为单位表示角的 大小时,弧度(rad )可以省略不写.度()ο 不可省略. 4.弧长公式、扇形面积公式:,r l α= 2||2 1 21r lr S α= =扇形,其中l 为弧长,r 为圆的半径.圆的周长、面积公式是弧长公式和扇形面积公式中当πα2=时的情形. 5.任意角的三角函数定义:设α是一个任意大小的角,角α终边上任意一点P 的坐标是()y x ,,它与原点的距离是 )0(>r r ,那么角α的正弦、余弦、正切、余切、正割、余割分别是 y r x r y x x y r x r y ====== ααααααcsc ,sec ,cot ,tan ,cos ,sin .这六个函数统称为三角函数. 三角函数 定义域 x y sin = R x y cos = R x y tan = ? ?????∈+≠Z k k x x ,2π π x y cot = {}Z k k x x ∈≠,π x y sec = ? ?????∈+≠Z k k x x ,2π π x y csc = {}Z k k x x ∈≠,π 7.三角函数值的符号:各三角函数值在第个象限的符号如图所示(各象限注明的函数为正,其余为负值) 可以简记为“一全、二正、三切、四余”为正. 二、疑难知识导析