中考数学二次函数与四边形综合专题

72

x = B(0,4)

A(6,0)

E

F

x

y

O

二次函数与四边形综合专题

一．二次函数与四边形的形状

例1. 如图，抛物线2

23y x x =--与x 轴交A 、B 两点（A 点在B 点左侧），直线l 与抛物线交于A 、C 两点，其中C 点的横坐标为2．

（1）求A 、B 两点的坐标及直线AC 的函数表达式；

（2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点，求线段PE 长度的最大值； （3）点G 是抛物线上的动点，在x 轴上是否存在点F ，使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F 点坐标；如果不存在，请说明理由．

解：（1）令y=0，解得11x =-或23x =∴A （-1，0）B （3，0）；将C 点的横坐标x=2代入2

23y x x =--

得y=-3，∴C （2，-3）∴直线AC 的函数解析式是y=-x-1 （2）设P 点的横坐标为x （-1≤x ≤2）则P 、E 的坐标分别为：

P （x ，-x-1），E （2(,23)x x x --

∵P 点在E 点的上方，PE=22(1)(23)2x x x x x -----=-++ ∴当1

2

x =

时，PE 的最大值=94

（3）存在4个这样的点F ，分别是1234(1,0),(3,0),(470),(47,0)F F F F -+-，

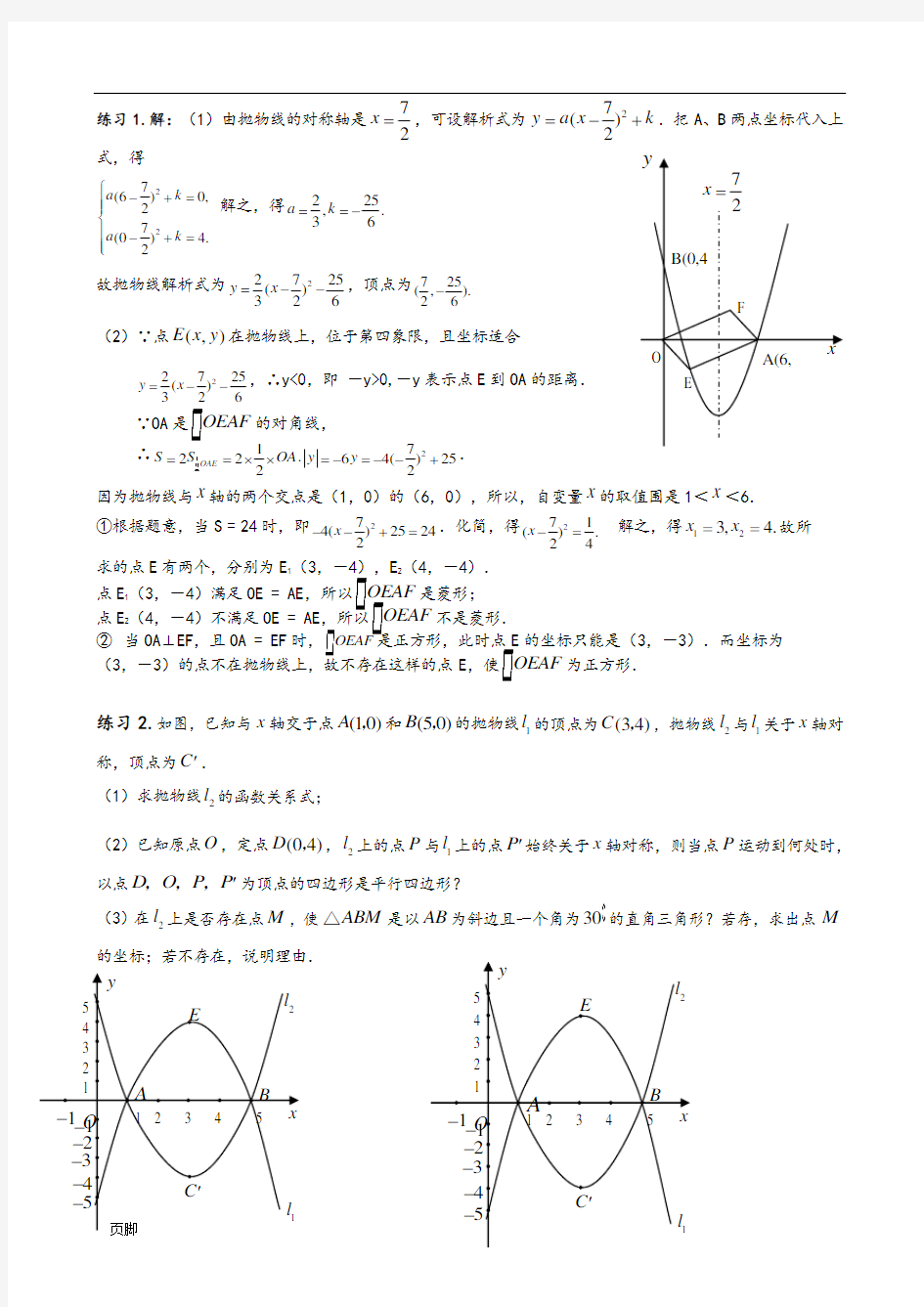
练习1.如图，对称轴为直线7

2

x =

的抛物线经过点A （6，0）和B （0，4）． （1）求抛物线解析式及顶点坐标； （2）设点E （x ，y ）是抛物线上一动点，且位于第四象限，四边形OEAF 是以OA 为对角线的平行四边形．求平行四边形OEAF 的面积S 与x 之间的函数关系式，并写出自变量x 的取值围； ①当平行四边形OEAF 的面积为24时，请判断平行四边形OEAF 是否为菱形？

②是否存在点E ，使平行四边形OEAF 为正方形？若存在，求出点E 的坐标；若不存在，请说明理由．

A

练习1.解：（1）由抛物线的对称轴是

7

2

x=，可设解析式为2

7

()

2

y a x k

=-+．把A、B两点坐标代入上式，得

2

2

7

(6)0,

2

7

(0) 4.

2

a k

a k

?

-+=

??

?

?-+=

??

解之，得225

,.

36

a k

==-

故抛物线解析式为2

2725

()

326

y x

=--，顶点为725

(,

26

-

（2）∵点(,)

E x y在抛物线上，位于第四象限，且坐标适合

2

2725

()

326

y x

=--，∴y<0，即－y>0,－y表示点E到OA的距离．

∵OA是OEAF的对角线，

∴2

17

2264()25

22

OAE

S S OA y y

==???=-=--+．

因为抛物线与x轴的两个交点是（1，0）的（6，0），所以，自变量x的取值围是1＜x＜6．

①根据题意，当S = 24时，即2

7

4()2524

2

x

--+=．化简，得2

71

(.

24

x-=解之，得12

3, 4.

x x

==故所

求的点E有两个，分别为E1（3，－4），E2（4，－4）．

点E1（3，－4）满足OE = AE，所以OEAF是菱形；

点E2（4，－4）不满足OE = AE，所以OEAF不是菱形．

②当OA⊥EF，且OA = EF时，OEAF是正方形，此时点E的坐标只能是（3，－3）．而坐标为

（3，－3）的点不在抛物线上，故不存在这样的点E，使OEAF为正方形．

练习2.如图，已知与x轴交于点(10)

A，和(50)

B，的抛物线

1

l的顶点为(34)

C，，抛物线

2

l与

1

l关于x轴对称，顶点为C'．

（1）求抛物线

2

l的函数关系式；

（2）已知原点O，定点(04)

D，，

2

l上的点P与

1

l上的点P'始终关于x轴对称，则当点P运动到何处时，以点D O P P'

，，，为顶点的四边形是平行四边形？

（3）在

2

l上是否存在点M，使ABM

△是以AB为斜边且一个角为30的直角三角形？若存，求出点M 的坐标；若不存在，说明理由．

练习3. 如图，已知抛物线

1

C与坐标轴的交点依次是(40)

A-，，(20)

B-，，(08)

E，．

（1）求抛物线

1

C关于原点对称的抛物线

2

C的解析式；

（2）设抛物线

1

C的顶点为M，抛物线

2

C与x轴分别交于C D

，两点（点C在点D的左侧），顶点为N，四边形MDNA的面积为S．若点A，点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；

与此同时，点M，点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A与点D重合为止．求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值围；

（3）当t为何值时，四边形MDNA的面积S有最大值，并求出此最大值；

（4）在运动过程中，四边形MDNA能否形成矩形？若能，求出此时t的值；若不能，请说明理由．

二．二次函数与四边形的面积

例1.如图10，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：

x …-3 -2 1 2 …

y …-

5

2

-4 -

5

2

0 …

(1) 求A、B、C三点的坐标；

(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，

并指出m的取值围；

(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，

若点M不在抛物线P上，求k的取值围.

图10

练习1.如图，平面直角坐标系中有一直角梯形OMNH ，点H 的坐标为（－8，0），点N 的坐标为（－6，－4）．

（1）画出直角梯形OMNH 绕点O 旋转180°的图形OABC ，并写出顶点A ，B ，C 的坐标（点M 的对应点为A ， 点N 的对应点为B ， 点H 的对应点为C ）； （2）求出过A ，B ，C 三点的抛物线的表达式；

（3）截取CE =OF =AG =m ，且E ，F ，G 分别在线段CO ，OA ，AB 上，求四边形BEFG 的面积S 与m 之间的函数关系式，并写出自变量m 的取值围；面积S 是否存在最小值?若存在，请求出这个最小值；若不存在，请说明理由；

（4）在（3）的情况下，四边形BEFG 是否存在邻边相等的情况，若存在，请直接写出此时m 的值，并指出相等的邻边；若不存在，说明理由．

练习2.如图，正方形ABCD 的边长为2cm ，在对称中心O 处有一钉子．动点P ，Q 同时从点A 出发，点P 沿A B C →→方向以每秒2cm 的速度运动，到点C 停止，点Q 沿A D →方向以每秒1cm 的速度运动，到点D 停止．P ，Q 两点用一条可伸缩的细橡皮筋联结，设x 秒后橡皮筋扫过的面积为2

cm y ．

（1）当01x ≤≤时，求y 与x 之间的函数关系式； （2）当橡皮筋刚好触及钉子时，求x 值；

（3）当12x ≤≤时，求y 与x 之间的函数关系式，并写出橡皮筋从触及钉子到运动停止时POQ ∠的变化围；

（4）当02x ≤≤时，请在给出的直角坐标系中画出y 与x 之间的函数图象．

B C

P

O D Q

A B

P

C

O

D

Q A

y

3

2 1 O

1 2 x

练习3. 如图，已知抛物线l1：y=x2-4的图象与x轴相交于A、C两点，B是抛物线l1上的动点(B不与A、C重合)，抛物线l2与l1关于x轴对称，以AC为对角线的平行四边形ABCD的第四个顶点为D.

(1) 求l2的解析式；

(2) 求证：点D一定在l2上；

(3) □ABCD能否为矩形？如果能为矩形，求这些矩形公共部分的面积(若

只有一个矩形符合条件，则求此矩形的面积)；如果不能为矩形，请说明

理由. 注：计算结果不取近似值

.

三．二次函数与四边形的动态探究

例1.如图1，在平面直角坐标系中，有一矩形纸片OABC，已知O(0，0)，A(4，0)，C(0，3)，点P是OA 边上的动点(与点O、A不重合)．现将△PAB沿PB翻折，得到△PDB；再在OC边上选取适当的点E，将△POE 沿PE翻折，得到△PFE，并使直线PD、PF重合．

(1)设P(x，0)，E(0，y)，求y关于x的函数关系式，并求y的最大值；

(2)如图2，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；

(3)在(2)的情况下，在该抛物线上是否存在点Q，使△PEQ是以PE为直角边的直角三角形？若不存在，说

明理由；若存在，求出点Q的坐标．

图1

图2

例2. 已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB

（1）求A、B、C三点的坐标；

（2）求此抛物线的表达式；

（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值围；（4）在（3）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

例3. 如图，矩形ABCD中，AB＝3，BC＝4，将矩形ABCD沿对角线A平移，平移后的矩形为EFGH（A、E、C、G始终在同一条直线上），当点E与C重时停止移动．平移中EF与BC交于点N，GH与BC的延长线交于点M，EH与DC交于点P，FG与DC的延长线交于点Q．设S表示矩形PCMH的面积，S'表示矩形NFQC的面积．

（1）S与S'相等吗？请说明理由．

（2）设AE＝x，写出S和x之间的函数关系式，并求出x取何值时S有最大值，最大值是多少？

（3）如图11，连结BE，当AE为何值时，ABE

?是等腰三角形．

练习1.如图12，四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）．点M从O出发以每秒

x

N

M

Q

P H

G

F

E

D

C

B

A

图11

Q

P

N

M

H

G

F

E

D

C

B

A

图10

2个单位长度的速度向A 运动；点N 从B 同时出发，以每秒1个单位长度的速度向C 运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N 作NP 垂直x 轴于点P ，连结AC 交NP 于Q ，连结MQ ． （1）点 （填M 或N ）能到达终点；

（2）求△AQM 的面积S 与运动时间t 的函数关系式，并写出自变量t 的取值围，当t 为何值时，S 的值最大；

（3）是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标，若不存在，说明理由．

练习2. 实验与探究

（1）在图1，2，3中，给出平行四边形ABCD 的顶点A B D ，，的坐标（如图所示），写出图1，2，3中的顶点C 的坐标，它们分别是(52)，， ， ；

（2）在图4中，给出平行四边形ABCD 的顶点A B D ，，的坐标（如图所示），求出顶点C 的坐标（C 点坐标用含a b c d e f ，，，，，的代数式表示）；

归纳与发现

（3）通过对图1，2，3，4的观察和顶点C 的坐标的探究，你会发现：无论平行四边形ABCD 处于直角坐标系中哪个位置，当其顶点坐标为()()()()A a b B c d C m n D e f ，，，，，，，（如图4）时，则四个顶

点的横坐标a c m e ，，，之间的等量关系为 ；纵坐标b d n f ，，，之间的等量关系为

x

图1

x

图2

x

图3

)

x

图4

图12