第五节振型向量正交性

第五节振型向量正交性
对多自由度系统振动问题的分析与两自由度系统没有本质上的区别。只是由于自由度上的增多导致数学上计算变得复杂多了。因此,在研究多自由度系统振动问题时,应找出一种便于分析的方法,这就是模态分析法(振型叠加法)。为此,首先讨论有关耦合与解耦的方法。
一、耦合与解耦(教材6.7和6.8)
举例说明什么是耦合与解耦。
D
y
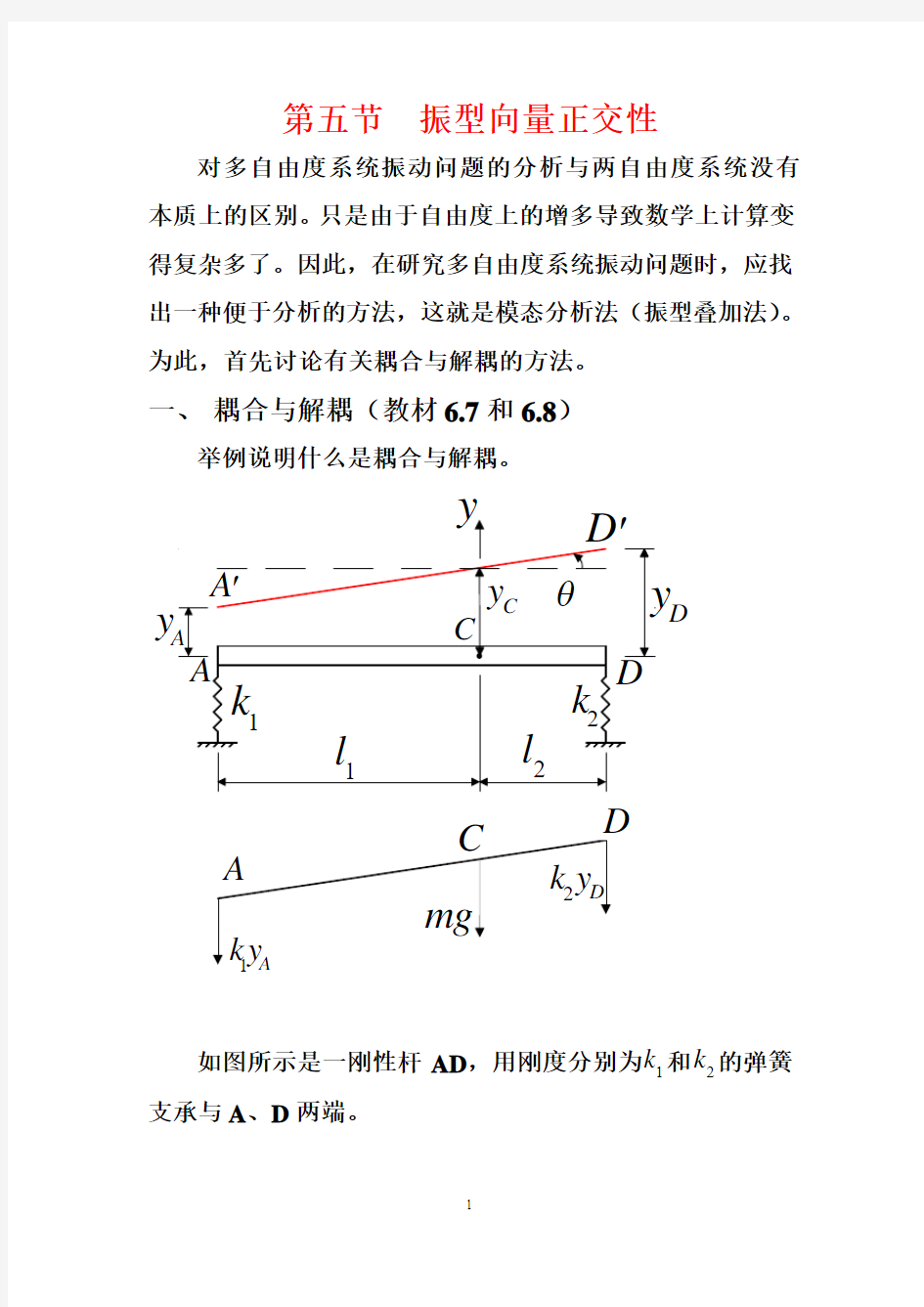
如图所示是一刚性杆AD,用刚度分别为
1
k和
2
k的弹簧支承与A、D两端。
(1) 取质心C 点的垂直位移C y 和刚性杆绕C 点的转角θ为广义坐标。则刚性杆在振动中任一瞬时的受力如图所示。由几何关系,得
12112212D A C A C D C D A l y l y y y y l l l y y l y y l l θ
θ
θ+?=?=-+??
??
?
=+-??=?+?
由牛顿运动定律,的系统的振动微分方程为
121122
C A D
A D my k y k y J k y l k y l θ=--??
=-? (a ) 式中m 是刚性杆AD 的质量,J 是刚性杆AD 绕质心C 的转动惯量。整理式(a ),得
()()()()12221122
221111220
C C C my k k y k l k l J k l k l y k l k l θθθ+++-=???+-++=?? (b ) 写成矩阵的形式
12221122221111220000C C y k k k l k l y m J k l k l k l k l θθ+-????????
??+=??????????-+?????
????? (c ) 在上式中,质量矩阵是一个对角矩阵,反映在方程组中,就是两个微分方程的第一个方程仅包含一个广义坐标的二阶导数(加速度)C y ,第二个方程仅包含另一个广义坐标的二阶导数θ,这种加速度(惯性力)之间没有耦合的情况,称之为惯性解耦。 刚度矩阵是非对角矩阵,反映在
方程组中,也就是两个微分方程的每一个方程都包含广义坐标C y 和θ,这种坐标之间有耦合的情况,称之为弹性耦合(静力耦合)。
(2)如果在杆上另取一点B ,令31AB l l e ==-,
42BD l l e ==+,其中e BC = ,且令
1324
k l k l =
以B 点的纵坐标B y 和杆的转角θ为广义坐标,则系统的振动微分方程为
12222
1324()0
()()0
B B B my me k k y mey J me k l k l θθθ?+++=??++++=?? 写成矩阵形式
1222213240
000
B B y k k m
me y k l k l me J me θθ+??????????
+=?
?????????++??
???????? 在新的坐标写出的方程中,刚度矩阵是一个对角矩阵,反映在方程组中,就是两个微分方程的第一个方程仅包含一个广义坐标B y ,第二个方程仅包含另一个广义坐标θ,这种坐标之间没有耦合的情况,称之为弹性解耦(静力解耦)。而质量矩阵是非对角矩阵,反映在方程组中,也就是两个微分方程的每一个方程都包含广义坐标的二阶导数C y 和θ,这种加速度(惯性力)之间有耦合的情况,称之为惯性耦合。
(3)若以弹簧支承处的位移A y 和D y 为广义坐标,则振动微分方程为
2111221211212122()()0
()()0
A D A D A D A D ml y ml y k l l y k l l y Jy Jy k l l l y k l l l y +++++=??
-+-+++=? 写成矩阵形式
1122122111212122()
()0()()0A A D D y k l l k l l y ml ml y k l l l k l l l y J J ++??????????+=??????????-++-??
????????由此可见此时,刚度矩阵和质量矩阵都不是对角矩阵,即方程组中同时存在着惯性耦合和弹性耦合。
有以上分析可以看出,同一个振动系统可以选择不同的广义坐标来建立它的运动方程。但若选择的坐标不同,系统的运动方程的形式和耦合情况也不同。这表明:运动方程的耦合并不是振动系统所固有的本性,而完全取决于坐标的选择。即[]k 和[]M 与选取的坐标系有关。换句话说,描述系统的坐标系不同,则[]k 和[]M 也不同。
我们知道,求解一个耦合的运动方程是十分复杂的,尤其是实际工程问题,有的系统自由度多达上百数千,因此即使利用计算机求解这样一个耦合的方程组,也是十分困难的。但如果选取的坐标恰好使系统的运动微分方程组的耦合项全等于零,既无弹性耦合,又无惯性耦合,也就是使质量矩阵和刚度矩阵同时为对角矩阵,那么n 个联立的微分方程就成为n 个独立的微分方程了,于是求解就很容易了。
二、振型正交性(教材6.12)
一个n 个自由度系统具有n 个固有频率和n 组对应的振型向量。设第i 阶固有频率为ni ω,对应的振型为{}i u ,则有如下的关系
[]{}[]{}2
ni i i k u M u ω= (a )
同样nj ω和{}j u 也满足
[]{}[]{}2nj j j k u M u ω= (b )
用{}T j u 前乘以(a )两端,用{}T
i u 前乘以(b )两端,得 {}[]{}{}[]{}2
T
T
ni j i j i u k u u M u ω
= (c )
{}[]{}{}[]{}2T T
nj
i j i j u k u u M u ω= (d )
因为[]k 和[]M 都是对称矩阵,则将(d )式两边转置,得 {}[]{}{}[]{}2T
T
nj
j i j i u k u u M u ω= (e )
(c )-(e ),得
{}[]{}2
2()0T
ni
nj
j i u M u ωω-= (f )
在一般情况下,当i j ≠时,ni nj ωω≠,所以有
{}[]{}0T
j i u M u = (4-45)
将上式代入(e )式,得
{}[]{}0T
j i u k u = (4-46)
式(4-45)和(4-46)表示,对应于不同固有频率的两个振
型向量之间存在着对质量矩阵[]M 和刚度矩阵[]k 的正交性。这个性质就称为振型向量正交性。
将式(a )两边前乘以{}T
i u ,得
{}[]{}{}[]{}2T T
ni
i i i i u k u u M u ω= (g )
令
{}[]{}(1,2,,)T
i i i
i n M u M u == (h )
因质量矩阵[]M 是正定的,则i M 总是一个正实数。称为第i
阶主质量。
令
{}[]{}(1,2,,)T
i i i
i n K u k u == (i )
称为第i 阶主刚度。 则由式(g ),得
{}[]{}{}[]{}2(1,2,,)T
i i i ni
T
i
i i
u k u K M u M i n u ω=== (j ) 由此可见,第i 阶固有频率的平方就等于第i 阶主刚度
除以第i 阶主质量。
三、主质量矩阵和主刚度矩阵
把n 个振型向量依次排列,构成一个n 阶方阵,记为
[]{}{}{}12
1112221
2
n n n n n n n u u u u u u u u u u u u u ???=??
??
??
??
??????????????????=???????????????
?????????????????
(6-44) 称为振型矩阵。则
[][][]{}{}{}[]{}{}{}{}[]{}{}[]{}{}[]{}{}[]{}{}[]{}{}[]{}{}[]{}{}[]{}{}[]{}121
2
1
112
1212221
2
=T T T
n T n T T
T
n T T
T
n T T
T
n n n n u u u M u M u u u u u M u u M u u M u u M u u M u u M u u M u u M u u M u ????
????=????
????????
??
??
?????????
?
注意到: {}[]{}0T
j i u M u = (i j ≠
)
和
{}[]{}T
i i i u M u M =
则上式变成
[][][]12
0000
00T n M M
u M u M
M ??
??
??????==???
?????
???
?
称为主质量矩阵(模态质量矩阵)。
同理,有
[][][]12
000
00T n K K
u k u K
K ??
??
??????==???
?????
???
?
称为主刚度矩阵(模态刚度矩阵)。
例题2:验证振型正交性。
对于图示系统(例1)
123m m m m ===,1234k k k k k ====
质量矩阵[]000000m M m m ????=??????,
刚度矩阵[]20202k k
k k k k k k -??
??=--??-????
系统的三个固有频率
123,,n n n ωωω=
=
=
振型向量为
{}{}{}12
3111,
0,111u u u ???????
??===?????????-??
??
?
?
证:
{}[]{
}120011100000110001T m u M u m m m m m m ??
????????=??????
??-????
????????==+-=??????-??
{}[]{
}1220111200211(22(2(201(20(20
T k k u k u k k k k k k k k k k -??
????????=--??
??????--????
????????=---??????-??=-+--=
{}[]{
}1111001
1000011241T
m M u M u m m m m m m m m ??
??????==????????????
??
??==++=?
?
????
{}[]{
}1111201120211(21)(21(21)(24(2T k k K u k u k k k k k k k k k k k k
??
-??????==--????
??-??????????=---??
????=-+-+-=-
2
11
14(2(24n K k k M m m
ω--===
四、正则振型向量和正则(主)坐标 1. 正则振型向量
由于振型向量仅表示各坐标间幅值的相对大小。因此,只有通过归一化,这才能确定振型向量中元素的具体数值。所以,如果归一化不同,则由振型向量构成的振型矩阵,按下式计算时
[][][]12
0000
00T n M M
u M u M
M ??
??
??????==???
?????
????
求得的主质量i M 的值各不相同。
故为了方便起见,将各阶振型向量正则化,令
{
}}1
(1,2,,)i i u i n ?=
= (6-48)
称为第i 阶正则振型向量。
{}[]{
}}[
}111
1(1,2,
,)
T
T
i i i i i i
M u M u M i n M ??=
=?==(6-49)
即正则振型向量所对应的主质量等于1。
{}[]{
}}[
}2
111(1,2,
,)
T
T
i i i i i ni
i
k u k u K i n M ??ω=
=?==(6-50)
即正则振型向量所对应的主刚度等于2
ni ω。
把n 个正则振型向量依次排列,构成一个n 阶方阵,记为
[]{}{}{
}
}}{}12
1211
1
n n n n u u u M ??????Φ=??
??=???
则矩阵
[]Φ称为正则振型矩阵。
由于正则振型向量是振型向量中的特定一组,因此正则振型向量也满足振型向量正交性。即
{}[]{}0(,1,2,,)T
j i M i j n i j ??==≠ {}[]{}0
(,1,2,
,)T
j i k i j n i j ??==≠
所以有
[][][][]T
M I ΦΦ=
[][][][]212
2
2n
T n nn k ωωω??
??
?
?ΦΦ==Λ????????
2. 正则(主)坐标
若以[]Φ为变换矩阵,
对原广义坐标{}x 进行线性变换,令
{}[]{}()()x t z t =Φ (6-51)
则
{}[]1
2
()T
n z t z z z = 称为正则主坐标,简称正
则坐标。将(6-51)式代入多自由度系统的振动微分方程,
得
[][]{}[][]{}{}()()()M z t k z t F t Φ+Φ=
上式两边前乘以
[]
T
Φ,
[][][]{}[][][]{}[]{}
()()()T
T
T
M z t k z t F t ΦΦ+ΦΦ=Φ令
{}[]{}()()T
P t F t =Φ (6-53)
为对应于正则坐标的激励力。则有
{}[]{}{}()()()z t z t P t +Λ= (6-52)
展开上式,得
2
11112
22222z ()
z ()
z ()n
n n nn n n
z P t z P t z P t ωωω?+=?+=??
?
?+=
? 上式是采用正则坐标来描述的系统振动微分方程,是最简单的运动方程式,它是n 个独立的微分方程。因而求解就很容易了。
a1,a2,a3是规范正交向量组,
竭诚为您提供优质文档/双击可除a1,a2,a3是规范正交向量组, 篇一:第三讲向量组 第三讲向量组 --------------------------------------------------- 向量作为工具可以描述空间中的点、矩阵中的行或列、线性方程组中的方程等等。研究向量的线性运算[加法与数乘]、向量组线性相关性、向量组的秩[矩阵秩]与最大无关组、等价向量组等概念可以解决线性方程组的理论。 向量组是线性代数的重难点之一,概念多,内容抽象,推理逻辑性强,描述要求准确,与矩阵、方程组相互交织,可以相互转换。例如,向量组秩、最大无关组是线性方程组解的判定、结构定理的理论基础;向量组的秩和相应矩阵秩一致,是向量组与矩阵结合点,反映了向量组和矩阵的本质。 向量组主要分三大部分: ■线性表示与线性相关性:向量的线性组合和线性表示;向量组的线性表示与等价向量组;向量组的线性相关性; ■向量组的秩:向量组的最大无关组与秩的概念、性质
及求法,向量组秩与矩阵秩关系;秩与线性相关性的关系; ■向量空间:向量空间及其基、维数;向量在基下的坐标;两基间的过渡矩阵;基的规范正交化: 正交阵及其性质。 教材:第四,第五章第1节。 ----------------------------------------------------------------------------------------- 一、主要内容 1、向量及其线性运算 ----概念 ------------------------------------------ (1)n个数组成的有序数组称为n维向量;写成一行的称为行向量,写成一列的称为列向量;若干个同维行(列)向量的集合称为向量组; (2)设有向量a(a1,a2,,an),b(b1,b2,,bn),实数kR,则下列运算 ka(ka1,ka2,,kan),ab(a1b1,a2b2,,anbn), 称为向量的线性运算; (3)设有向量组a1,a2,,an和向量b,若存在常数 k1,k2,,kn,使得有 bk1a1k2a2knan,
向量正交化
Gram-Schmidt 正交化方法 正射影 设欧式空间V 中向量s ααα ,,21线性无关,令 ;11αβ= 11 11 22,,ββββααβ-=; (1) 22 2231111333,,,,ββββ αββββααβ-- =; (11) 11 22221111,,,,,,--------=s s s s s s s s s ββββαββββαββββααβ . 则s βββ,,,21 均非零向量,且两两正交.再令,1 i i i ββγ= s i ,.2,1 = 则},,,{21s γγγ 为规范正交组. 将(1)重新写成i i i i i i t t βββα+++=--11,11, , s i ,,2,1 = 其中k k k i ik t βββα,,= ,,,,2,1s i = .1,,2,1-=i k {}, ,,2,1,s j i ∈? 有 ∑∑-=-=++= 1 1 1 1 ,,j k j k jk i k i k ik j i t t ββββαα()???? ? ?? ? ?? ??? ????????? ? ? =-001,000,000,0,,0,1,,,1112222111,21 j j j i i i i t t t t t t ββββββ 令??????? ? ? ?=---10 001001011,2,2,11,1,121 s s s s s s t t t t t t T
则 T T s s s s s s s s s s s s s s ??????? ? ??=????? ? ?? ? ?-----ββββββββααααααααααααααααααααααα,0 00 0,0000,0 000,,,,,,,,,,,,,1 12211/2 1 1211122 21 212111 上式左端的实方阵是s ααα,,,21 的格兰母矩阵,记为:()s G ααα,,,21 ,上式右端中 间 的 对 角 阵 是 s βββ,,,21 的Gram 矩阵.即 有:()()T G T G s s βββααα,,,,,,21/21 = 因此()()s s s s G G βββββββββααα,,,,,,det ,,,det 22112121 == 注意:对任意一个向量组,无论它是线性相关,还是线性无关,它总有Gram 矩阵(或者事先给出定义). 例1 设s ααα,,,21 欧式空间V 中向量,则 (1)()?≠0,,,det 21s G ααα s ααα,,,21 线性无关; (2)()?=0,,,det 21s G ααα s ααα,,,21 线性相关. 证明:只证(2) )?设s ααα,,,21 线性相关,则存在一个向量,不妨设为1α,可由其余向量线性 表示: s s k k ααα++= 221给s 阶的行列式()s G ααα,,,det 21 的第i 行乘数()i k -加到 第1行,s i ,,3,2 =得 ( )s s s s s s i s i i s s i i i s i i i s k k k G αααααααααααααααααααααααααα,,,,,,,,,,,,,,,det 21 22 21 22 12 2 212 1 1121 ∑∑∑===---= 0= )?法一:由上页证明推理过程立即得证。 法二:当()0,,,det 21=s G ααα 时,()s G ααα,,,21 的行向量组线性相关,因此存在不全为零的实数12,,,s k k k ,使
§4.4 向量的正交化
例4-13 证明)0,21,21(1=α ,)0,2 1 ,21(2-=α ,)1,0,0(3=α 是R 3的一组标准正交基. 分析:证明已知量是一组标准正交基,可以分两步证明: (1)证明所给向量两两正交,且为基. 方法:求所给向量的两两内积,如果内积等于零,则两向量正交; (2)每个向量的长度等于1. 方法:求每个向量的长度,判断长度是否等于1. 证明: (1)证明所给向量两两正交. 000)2 1(21212121=?+- ?+ ?= ?αα ,所以,1α 与2α 正交; 01002 102131=?+?+ ?= ?αα ,所以,1α 与3α 正交; 0100)2 1(02132=?+?- +?= ?αα ,所以,3α 与2α 正交; 有以上证明可知,所给向量1α 、2α 、3α 两两正交. 又由于三个向量都是3维向量,所以1α 、2α 、3α 是R 3的一组正交基. (2)证明1α 、2α 、3α 的长度都是1. 10 )2 1( )21(2 22 1=++= α ; 10 )2 1()2 1( 2 22 2=+- += α ; 11002 2 2 3=++= α . 有以上证明可知,所给向量1α 、2α 、3α 是R 3的一组标准正交基. 例4-14 设)3,2,1(=α ,)3,1,4(-=β 是R 3中的向量, 试求α 在β 上的投影向量,投影长度;β 在α 上的投影向量和投影长度. 解:βα ?=1×4+2×(-1)+3×3=11, 14321222=++=α , 263)1(42 22=+-+=β , α 在β 上的投影向量为 )3,1,4(2611)3,1,4()26(112 21-=-=?=ββ βαγ α 在β 上的投影纯量,或称为投影长度为 26111=?=β βαγ β 在α 上的投影向量为 )3,2,1(1411)3,2,1()14(112 22==?=αα βαγ β 在α 上的投影纯量或称为投影长度为
线性代数第六章向量空间及向量的正交性讲义
一、n 维向量的定义及运算 一、n 维向量的定义及运算二、向量空间 二、向量空间第一节向量空间 第二节向量的正交性
一、向量空间及其维数和基 一、向量空间及其维数和基 二、向量在基下的坐标 二、向量在基下的坐标
例1 设V 是一些n 维实向量的组成的非空集合,如果V 关 于向量的加法与数乘封闭(线性运算封闭),即 (1) ?a , b ∈V , 有a +b ∈V . (2) ?a ∈V , k ∈R , 有k a ∈V . 则称V 是一个实向量空间. 一、向量空间及其维数和基 定义1全体n 维向量的集合{(x 1, x 2, …, x n )T | x i ∈R ,i=1, 2, …, n }是一个向量空间,记为R n . 特别的 n = 1 时全体实数R 是一个向量空间; n = 3 时全体三维向量{(x 1, x 2, x 3)T |x i ∈R ,i= 1, 2, 3 } 是一个向量 空间,记为R 3. n = 2 时全体平面中的向量{(x 1, x 2 )T | x i ∈R ,i=1, 2} 是一个向量空 间,记为R 2. 注:向量空间中必含有零向量。
例3 例2而W = {(a 1, a 2, …, a n )T |}01∑==n i i a 是一向量空间. }1|),,,{(1 21∑==…=n i i T n a a a a S 不是一向量空间, 因为它关于加法与数乘均不封闭,也不含零向量.仅含一个n 维零向量0=(0, 0, …, 0)T 的集合{0}构成一 个向量空间,称为零空间.除零空间之外的所有向量空间均称为非零空间。 设V 是一个向量空间,W V , W ≠?. 如果W 关于向量的加法与数乘也封闭,则称W 是V 的子空间. 定义2若W V ,并且V W , 则称两个向量空间相等,记为W=V. ???
施密特正交化)
施密特正交化 在中,如果上的一组向量能够张成一个,那么这一组向量就称为这个子空间的一个基。Gram-Schmidt正交化提供了一种方法,能够通过这一子空间上的一个基得出子空间的一个,并可进一步求出对应的。 这种正交化方法以和命名,然而比他们更早的(Laplace)和(Cauchy)已经发现了这一方法。在李群分解中,这种方法被推广为()。 在数值计算中,Gram-Schmidt正交化是的,计算中累积的舍入误差会使最终结果的正交性变得很差。因此在实际应用中通常使用或进行正交化。 记法 ?:为n的内积空间 ?:中的元素,可以是向量、,等等 ?:与的 ?:、……张成的 ?:在上的 基本思想 图1v在V2上投影,构造V3上的正交基β Gram-Schmidt正交化的基本想法,是利用投影原理在已有正交基的基础上构造一个新的正交基。 设。V k是V n上的k维子空间,其标准正交基为,且v不在V k上。由投影原理知,v与其在V k上的投影之差 是正交于子空间V k的,亦即β正交于V k的正交基ηi。因此只要将β单位化,即 那么{η 1,...,η k+1 }就是V k在v上扩展的子空间span{v,η 1 ,...,η k }的标准正交 基。
根据上述分析,对于向量组{v 1,...,v m }张成的空间V n,只要从其中一个向量(不 妨设为v 1)所张成的一维子空间span{v 1 }开始(注意到{v 1 }就是span{v 1 }的正交 基),重复上述扩展构造正交基的过程,就能够得到V n的一组正交基。这就是Gram-Schmidt正交化。 算法 首先需要确定扩展正交基的顺序,不妨设为。Gram-Schmidt正交化的过程如下: 这样就得到上的一组正交基,以及相应的标准正交基。 例 考察如下R n中向量的,欧氏空间上内积的定义为
第五节振型向量正交性
第五节振型向量正交性 对多自由度系统振动问题的分析与两自由度系统没有本质上的区别。只是由于自由度上的增多导致数学上计算变得复杂多了。因此,在研究多自由度系统振动问题时,应找出一种便于分析的方法,这就是模态分析法(振型叠加法)。为此,首先讨论有关耦合与解耦的方法。 一、耦合与解耦(教材6.7和6.8) 举例说明什么是耦合与解耦。 D y 如图所示是一刚性杆AD,用刚度分别为 1 k和 2 k的弹簧支承与A、D两端。
(1) 取质心C 点的垂直位移C y 和刚性杆绕C 点的转角θ为广义坐标。则刚性杆在振动中任一瞬时的受力如图所示。由几何关系,得 12112212D A C A C D C D A l y l y y y y l l l y y l y y l l θ θ θ+?=?=-+?? ?? ? =+-??=?+? 由牛顿运动定律,的系统的振动微分方程为 121122 C A D A D my k y k y J k y l k y l θ=--?? =-? (a ) 式中m 是刚性杆AD 的质量,J 是刚性杆AD 绕质心C 的转动惯量。整理式(a ),得 ()()()()12221122 221111220 C C C my k k y k l k l J k l k l y k l k l θθθ+++-=???+-++=?? (b ) 写成矩阵的形式 12221122221111220000C C y k k k l k l y m J k l k l k l k l θθ+-???????? ??+=??????????-+????? ????? (c ) 在上式中,质量矩阵是一个对角矩阵,反映在方程组中,就是两个微分方程的第一个方程仅包含一个广义坐标的二阶导数(加速度)C y ,第二个方程仅包含另一个广义坐标的二阶导数θ,这种加速度(惯性力)之间没有耦合的情况,称之为惯性解耦。 刚度矩阵是非对角矩阵,反映在
第一讲正交向量组及施密特正交法
第一讲 Ⅰ 授课题目: §5.1 预备知识:向量的内积 Ⅱ 教学目的与要求: 1.了解向量的内积及正交向量组的概念; 1.了解把线性无关的向量组正交规范化的施密特(Smidt)方法; 2.了解正交矩阵概念及性质。 Ⅲ 教学重点与难点: 重点:正交向量组及正交矩阵 难点:施密特正交化方法 Ⅳ 讲授内容: 一、向量的内积 前面曾介绍过向量的线性运算,但在许多实际问题中,还需要考虑向量的长度等方面的度量性质.在此,作为解析几何中向量的数量积的推广,引进向量的内积运算. 定义1 设有n 维向量 ??????? ??=n x x x x 21,?????? ? ??=n y y y y 21, 令 []n x y x y x y x +++= 2211,, []y x ,称为向量x 与y 的内积. 内积是向量的一种运算,用矩阵记号表示,当x 与y 都是列向量时,有 []y x y x T =,. 内积具有下列性质(其中z y x ,,为n 维向量,λ为实数): ① [][]x y y x ,,=; ② [][]y x y x ,,λλ=; ③ [][][]z x y x z y x ,,,+=+.
例1 设有两个四维向量??????? ??-=5121α,???? ?? ? ??--=56 03β.求[]βα,及[]αα,. 解 []3425603,-=--+-=βα []3125141,=+++=αα n 维向量的内积是数量积的一种推广,但n 维向量没有3维向量那样直观的长度和夹 角的概念,因此只能按数量积的直角坐标计算公式来推广.并且反过来,利用内积来定义 n 维向量的长度和夹角: 定义2 令x = []2 2221,n x x x x x ++= ,则x 称为n 维向量x 的长度(或范数). 向量的长度具有下列性质: ① 非负性 当0≠x 时,0>x ,当0=x 时,0=x ; ② 齐次性 x x λλ=; ③ 三角不等式 y x y x +≤+. 向量的内积满足施瓦兹不等式 [][][]y y x x y x ,,,2 ?≤ 由此可得 [] 1 ,≤y x y x (当0y ≠x 时) 于是有下面的定义: 当0≠x ,0≠y 时, [] y ,arccos x y x =θ 称为n 维向量的夹角. 二、正交向量组 当[]0,=y x 时,称向量x 与y 正交.显然,若0=x ,则x 与任意向量都正交. 两两正交的非零向量组称为正交向量组. 定理 1 若n 维向量r ααα ,,21是一组两两正交的非零向量组,则r ααα ,,21线性无关. 证明 设有r λλλ ,,21使 02211=+++r r αλαλαλ ,
