正态分布
一、正态分布
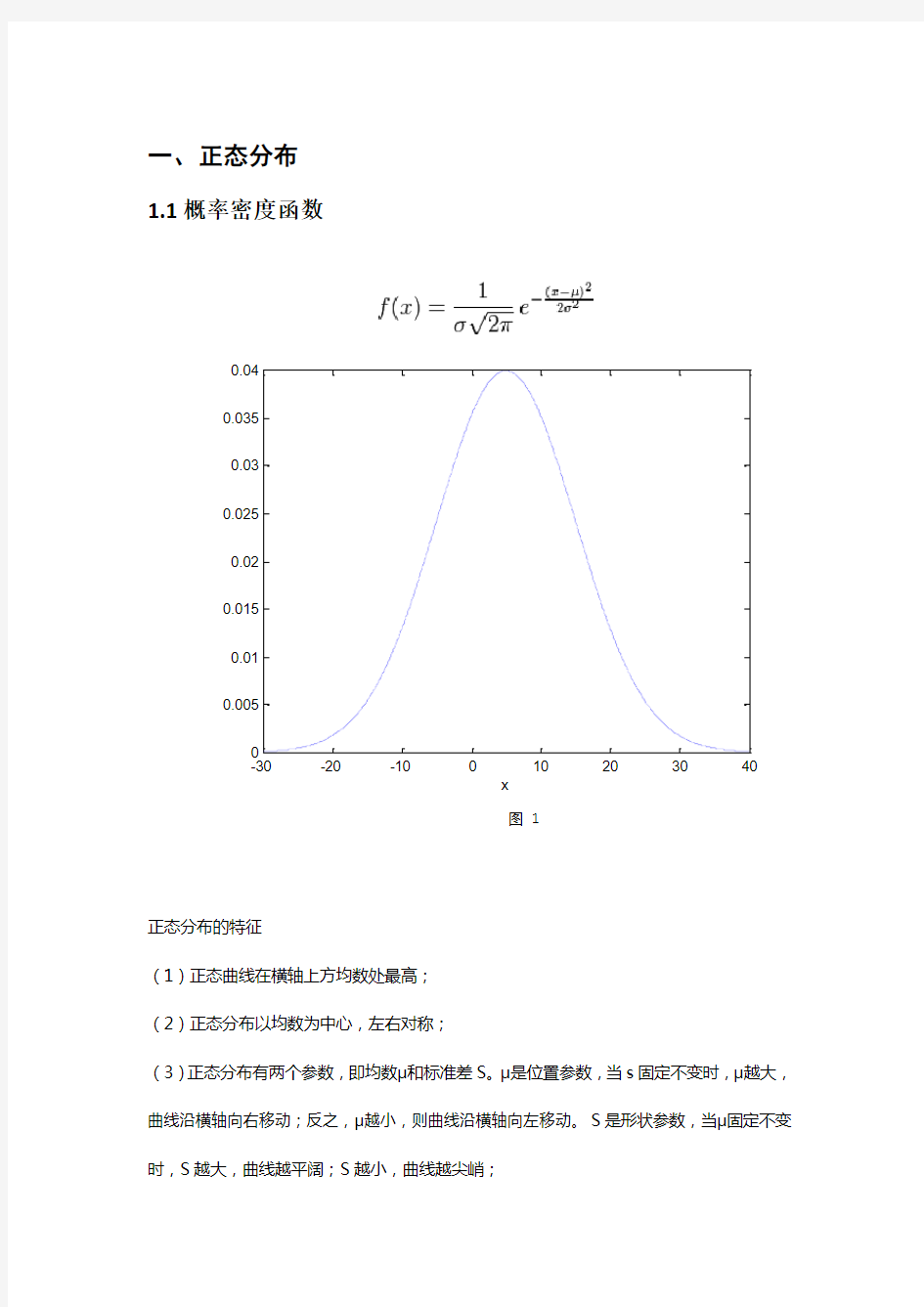
1.1概率密度函数
正态分布的特征
(1)正态曲线在横轴上方均数处最高;
(2)正态分布以均数为中心,左右对称;
(3)正态分布有两个参数,即均数μ和标准差S。μ是位置参数,当s固定不变时,μ越大,曲线沿横轴向右移动;反之,μ越小,则曲线沿横轴向左移动。S是形状参数,当μ固定不变时,S越大,曲线越平阔;S越小,曲线越尖峭;
(4)正态曲线下面积的分布有一定规律:
①正态分布时区间(μ-1s,μ+1s)的面积占总面积的68.27%;②正态分布时区间(μ-1.96s,μ+1.96s)的面积占总面积的95%;③正态分布时区间(μ-2.58s,μ+2.58s)的面积占总面积的99%。
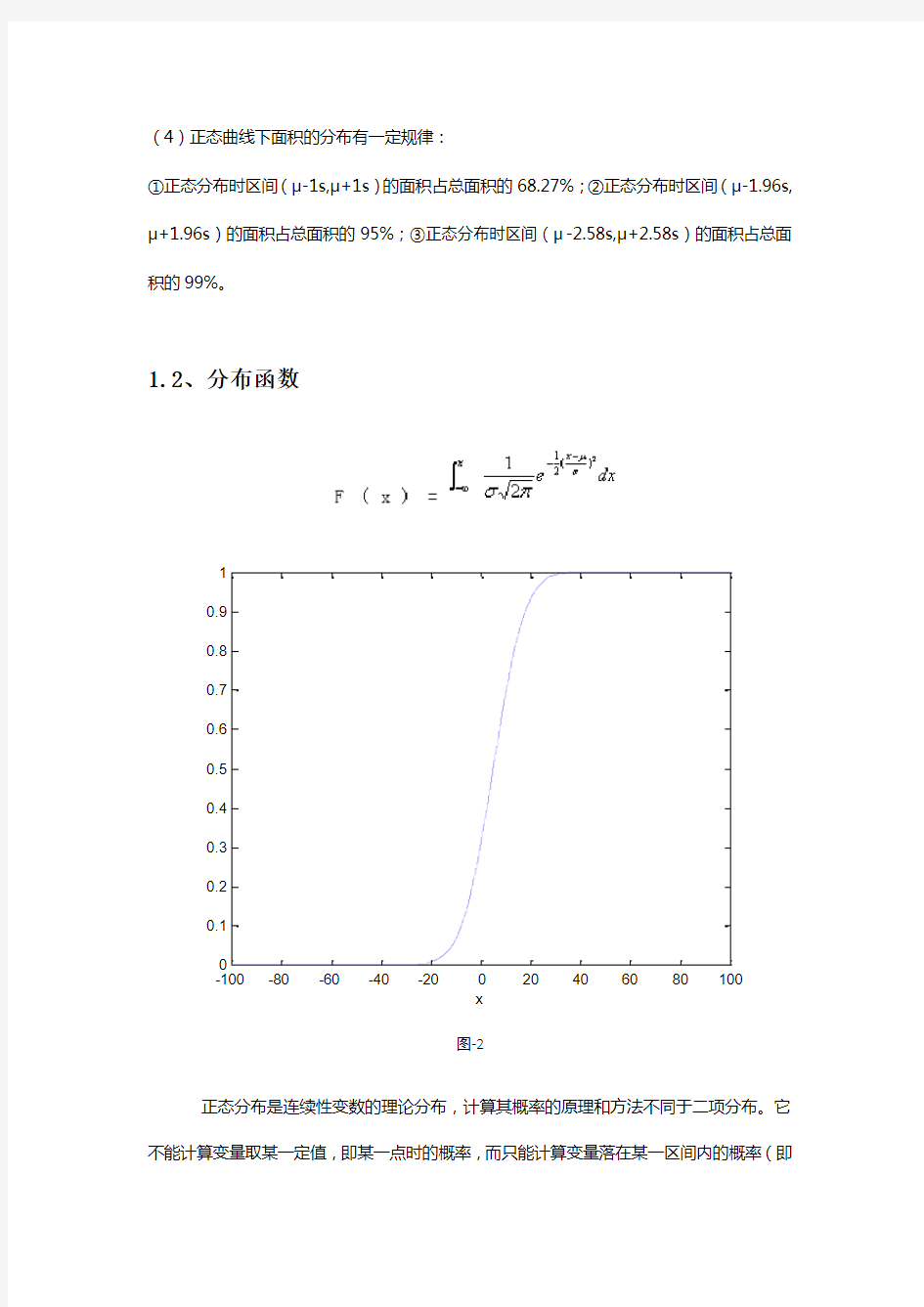
1.2、分布函数
图-2
正态分布是连续性变数的理论分布,计算其概率的原理和方法不同于二项分布。它不能计算变量取某一定值,即某一点时的概率,而只能计算变量落在某一区间内的概率(即
概率密度)。
对于任何正态分布随机变量x 落入任意区间(a ,b )的概率可以表示为:P(a 1.3、正态分布可度函数 图3 1.4、正态分布失效率函数 (x) =f(x)/R(x) 图 4 1.5、应用、问题、案例 考察某个工程的质量,由于偶然误码差的存在,其实际质量评分是不相同的,如将所有的数值按一定的组距进行大小分组整理,每组的分值个数叫做频率。以频率为纵坐标,数值为横坐标,可求出各组坐标,用线段把这些点连接起来,就可得到“中间高,两边低,左右近似对称”的折线。这折线叫实验分布曲线。由于它近似于理论分布曲线,可根据理论分布曲线的数学表达式,对工程质量的情况进行研究和讨论。 这就是说,废品率-=1--合格率。当质量评分分布曲线符合正态分布时,在士3s的范围内,实际上几乎包含了整个工程质量评分数。 单位混凝土预制构件厂1999 年3 ~6 月份为某电厂生产混凝土预制桩过程中混凝土试块抗压实验数据为例 用正态分布法检查混凝土构件的质量 。根据甲方要求 混凝土预制桩设计强度等级为C35平均强度达到C35 以上即35N mm2 为合格同时为了和致造成浪费规定其上限值不能高于设计强度的20 即42N mm 。其测试数据见表 我们把组距为1. SN/mm2,对以上数据进行分组,每组中数据个数就是频数m;,把有关数值列成表2 算数平均值=41 .078 (N/mm2) 标准差=3 .024 (N/mm2) 根据表2,第二、三两栏资料,画出实验分布曲线见图3中的虚线条形“频数分布直方图”分散范围66=6X 3. 024=18.144 (N/mm2),或写成士9. 024(N/mm2(,画出正态分布曲线,根据规定,大于35 . 00(N/mm2)且小于42 . OON/r之间的为合格品,所以合格品分为A,B两部分计算。则合格率为} (ZA ) = 0. 4778,不合格率为(ZA )' = 0. 0222则合格率为.(ZB)> = 0 .1779,不合格率为:=0.3821,则废品总率为ZA = 0 . 0222 +0 . 3821 = 0 . 4043 即有40.43%属废品。这说明:超下限的废品率2.22%不算太大,混凝土质量基本上是好的;但超过上限的废品率为38.21 0 o,虽不能算作废品,但毕竟是个很大的浪费,尤其在当 前,某些施工单位常以多有水泥来提高混凝土强度,这是技术经济管理上所不能允许的。应该采取措施,适当降低平均值(x)为缩小标准差(6},以求得即满足质量要求,又符合经济的原则。 通过以上分析,我们可以看出,运用正态分布对工程中的质量问题进行分析和评定,可随时控制和掌握生产过程的质量动态,并针对生产过程中出现的质量问题,及时采取措施和对策以解决,从而保证生产质量始终处于控制状态,最终达到生产质量的稳定,并可降低成本,提高经济效益。同时也可促进和提高质量管理工作的效益和效率。 二、对数正态分布 2.1、概率密度函数 图5 变量的频数或频率呈中间最多,两端逐渐对称地减少,表现为钟形的一种概率分布。σ的大小改变图形的高度与峰值的大小,μ决定图形的位置。若X 是一个随机变量,Y=ln(X)服从正态分布:Y=ln(X)~N(μ,σ2)则称X 服从对数正态分布。μ和σ不是对数正态分布的均值和标准差,而分别称为它的对数均值和对数标准差。期望与方差分别是: 2.2、分布函数 图6 2.3、可靠度函数 图7 2.4、失效率函数 图8 2.5、应用、问题、案例 半导体器件的沾污、扩散、电流密.度和电压梯度等引起的器件失效,都可以看作是化学的或物理化学的过程所产生的结果,因此在半导体器件的寿命和加速寿命试验中,对数正态分布得到了广泛的应用。另外,对数正态分布还适合于电子设备维修时问的数学模型和反映电子元器件的可靠性增长过程。 钢筋混凝土结构的耐久性可靠性分析是内容复杂且丰富的研究课题,涉及的学科多.美国混凝土学会201委员会将混凝土耐久性破坏的过程概括为冻融循环君化学侵蚀卿磨蚀缪 钢筋锈蚀卿碱骨料反应.与耐久性有关的随机变量统计参数的观测和统计分析是结构耐久性评估的基础工作,但当前的诸如碳化深度、氯离子侵深度等实测资料相等缺乏,因而其变量分布概型,碳化深度或氯离子锈蚀深度预测等问题都有待进一步研究.。 对于在0- t1段上的任意时点t混凝土碳化深,度(或氯离子侵蚀深度)x可以调查,从而可建立其极限状态方程为:Z=D-x=0。式中,D为混凝土保护层的厚度;;x为碳化(或氯离子侵蚀)深度. 最保守的寿命预测或结构使用性能评估应认为Z> 0时为结构可靠状态.而Z<0结构则处于耐久性失效状态. 对于x的实测值处理,文献[4狱均匀锈蚀(大气环境下)x 近似服从正态分布;而局部锈蚀(海洋环境氯离子侵蚀)x应用极值I型分布近似描述.但由于前述原因,x的分布类型还不能完全肯定,由此,可用上述拟对数正态分布的优势,将x拟合成对数正态分布,至于D,可按正态分布计算。 根据对数正态分布的特点,根据在役工程结构实际情况(可能原变量的变异系数较大),对在役结构可靠度分析中常遇到的各类非对数正态分布随机变量,采用比正态分布形态更丰富的对数正态分布来描述;讨论了拟对数正态分布验算点法(对应于JC法中的当量正态分布法),其计算较简单,且精度更高;通过对钢筋混凝土钢筋锈蚀的耐久性可靠度分析,说明了拟对数正态分布法可应用于在役结构可靠性的分析。 三、威布尔分布 3.1、概率密度函数 图9 其中β为形状参数η为尺度参数 to为位置参数 形状参数决定了曲线的形状β>1时,密度函数曲线为单峰型,且随值的减小峰逐渐降低,在3-4时,接近于正态分布当为1时三参数变为两参数指数分布密度函数。位置参数to反映了函数在横轴上的位置变化,在可靠性分析中,to有极限的含义,也称为最小寿命。η尺度参数是当to=0时威尔布分布的特征寿命。β为函数中最有意义的参数。 3.2、分布函数 图10 3.3、可靠度函数 R(x) =1-F(x) 图11 3.4、失效率函数 (t)=f(t)/R(t) 图12 3.5、应用、问题、案例 威布尔分布是一种连续分布,它能够描述各种类型机械零部件失效数据的分布规律,在寿命数据分析、可靠性设计、疲劳可靠性分析、维修决策、保修策略制定等方面得到了一定程度的应用。标准的威布尔分布有二参数和三参数两种形式。常用来估计威布尔分布参数的方法可以分为两大类,图解法和解析法。图解法包括经验分布图法、威布尔概率图法和风险率统计图法等;解析法包括极大似然估计法和回归估计法等。这些传统的参数估计方法在样本数据较少时,难以获得较好的结果。 在一些样本数据较为复杂的条件下,比如不同失效模式的数据、不同质量的产品失效数据混合在一起时,传统的威布尔分布不能得到令人满意的拟合结果,传统的参数估计方法也不适用。在可靠性和统计学文献中,提出了在威布尔分布基本模型基础之上的改进模型,如混合模型、分段模型和竞争风险模型等,对于这三种模型的应用和参数估计方法目前也有了一些研究。 (1)基于支持向量回归机(Support Vector Regression,SVR)的威布尔分布参数估计。支持向量回归机是在统计学习理论基础上发展的用于预测输入输出量之间函数关系的一种方法,可以实现线性回归和非线性回归,特别适合于小样本情况。建立威布尔分布的线性回归估计模型,用支持向量回归机求解回归模型中的未知参数,从而获得威布尔分布的形状参数和位置参数的估计值,并讨论支持向量回归机在小样本和大样本条件下的适用性及在小样本条件下的优势。 (2)疲劳剩余寿命可靠性建模。疲劳可靠性中的一个重要问题就是疲劳剩余寿命预测,现有的研究大多是假设疲劳寿命服从正态分布或对数正态分布。威布尔分布在中、长寿命区都适用,也是描述疲劳寿命分布的理想模型。 (3)疲劳寿命服从威布尔分布的P-S-N曲线参数估计。在抗疲劳设计中常用到S-N曲线,考虑疲劳寿命可靠度的一组S-N曲线称为P-S-N曲线,它是进行疲劳可靠性设计的基础工具。获取P-S-N曲线的传统方法是成组试验法,将各种应力水平下疲劳寿命分布曲线上可靠度相等的点用光滑曲线连接而成。假定在各应力水平下,疲劳寿命为独立同分布随机变量,分别服从一个三参数威布尔分布,S-N曲线采用三参数方程来描述,通过寻找疲劳寿命可靠度函数与S-N曲线方程之间的关系,建立非线性方程组,其中的未知数即为S-N 曲线方程的三个参数。通过求解非线性方程组,可以获得各种可靠度时的,S-N曲线方程系数,从而可以求解P-S-N曲线方程的表达式。 威布尔分布由于含有二个或三个参数,与指数分布相比多了一个形状参数m。因此,它比指数分布适应能力强,对浴盆曲线的三个失效阶段,即早期失效型、偶然失效型、耗损失效型都可以适应。在航天产品中,普遍认为惯性平台产品其寿命遵从威布尔分布。 当形状参数m<1时,威布尔的失效率,随着产品工作时间的增加而减少,m越小,减少得越快。当m> 1时,威布尔的失效率,随着产品工作时间的增加而增大,m越大,增大得越快。而当m=1时,就成为指数分布,失效率为常数,与产品工作时间无关。这正好对应于浴盆曲线的早期失效型,耗损失效型和偶然失效型三种情况。 可靠性评估中采用信息折合是一种普遍使用的方法,文献对二参数威布尔分布且形状参数m已知的信息折合提出了一种方法,即若有n,台产品试验到t,时刻没有失效,而产品的任务时间为t。小时,则试验信息可折合为执行n次没有失效.这样就可以通过执行任 务的成败次数来评估产品的可靠度。 上述方法在寿命服从威布尔分布的一次性使用产品上可以得到很好的应用。例如,液体 火箭发动机是一次性使用产品,假定该型发动机的额定工作时间2分钟,通过长寿命地而试车例如4分钟来获得更多的信息。但对于要多次使用的产品(包含测试),例如惯性平台,每次定期检测中都要通电工作,最后上天时产品已经工作了一段时间,折合时就要谨慎一些。 以失效率为桥梁,利用热储备系统求解温储备系统的可靠度,避免了用可靠度的定义直接求解或运用马尔可夫理论求解的繁琐,并且可以将此方法扩展到冷储备系统。在计算时,可以用此算法同时处理三种储备系统,便于编程实现。实例证明了此方法的有效性。 四、指数分布 4.1、概率密度 其中λ > 0是分布的一个参数,常被称为率参数即每单位时间内发生某事件的次数。指数分布的区间是[0,∞)。如果一个随机变量X呈指数分布,则可以写作:X~ Exp(λ)。指数函数的一个重要特征是无记忆性。这表示如果一个随机变量呈指数分布当s,t≥0时有P(T>s+t|T>t)=P(T>s)即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。 4.2、分布函数 图14 4.3、可靠性函数 R(x) =1-F(x) 图15 4.5、应用、问题、案例 在概率论和统计学中,指数分布是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况,产品的失效是偶然失效时,其寿命服从指数分布。指数分布可以看作当威布尔分布中的形状系数等于1的特殊分布,指数分布的失效率是与时间t无关的常数,所以分布函数简单。 在电子元器件的可靠性研究中,通常用于描述对发生的缺陷数或系统故障数的测量结果。这种分布表现为均值越小,分布偏斜的越厉害。 指数分布应用广泛,在日本的工业标准和美国军用标准中,半导体器件的抽验方案都是采用指数分布。此外,指数分布还用来描述大型复杂系统(如计算机)的平均故障间隔时 间MTBF的失效分布。但是,由于指数分布具有缺乏“记忆”的特性.因而限制了它在机械可靠性研究中的应用,所谓缺乏“记忆”,是指某种产品或零件经过一段时间t0的工作后,仍然如同新的产品一样,不影响以后的工作寿命值,或者说,经过一段时间t0的工作之后,该产品的寿命分布与原来还未工作时的寿命分布相同,显然,指数分布的这种特性,与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的,它违背了产品损伤累积和老化这一过程。所以,指数分布不能作为机械零件功能参数的分布形式。 指数分布虽然不能作为机械零件功能参数的分布规律,但是,它可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型,特别是在部件或机器的整机试验中得到广泛的应用。 在电子元器件的可靠性研究中,指数分布应用广泛,在日本的工业标准和美国 军用标准中,半导体器件的抽验方案都是采用指数分布.假定某种产品的使用寿命服从指数分布,那么指数分布随机变量的无记忆性表明,无论它已经被使用了多长一段时间x,只要还没有损坏,它能再使用一段时间v的概率与一件新产品能使用到时间v的概率一样.就是说,这种产品将“永远年轻”.显然,指数分布的这种特性,与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的,它违背了产品损伤累积和老化这一过程.所以,指数分布不能作为机械零件功能参数的分布形式.这说明以指数分布作为寿命分布是有缺陷的.尽管如此在有些场合人们还是愿意采用这种易于计算的分布作为寿命的模型. 标准正态分布表 集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY- 标准正态分布表 4432198653 1.80.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0.970 6 1.90.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0.975 6 0.976 2 0.976 7 20.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.10.982 1 0.982 6 0.983 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0.985 4 0.985 7 2.20.986 1 0.986 4 0.986 8 0.987 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.989 2.30.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.40.991 8 0.992 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.50.993 8 0.994 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.60.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0.996 1 0.996 2 0.996 3 0.996 4 2.70.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0.997 1 0.997 2 0.997 3 0.997 4 2.80.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0.998 1 2.90.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x00.10.20.30.40.50.60.70.80.9 30.998 7 0.999 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 正态分布概率表 Φ( u ) = t分布介绍 在概率论和统计学中,学生 t - 分布(t -distribution ),可简称为 t 分布,用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。 t 分布曲线形态与 n(确切地说与自由度 df )大小有关。与标准正态分布曲线相比,自由度df 越小, t 分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度 df 愈大, t 分布曲线愈接近正态分布曲线,当自由度 df= ∞时, t 分布曲线为标准正态分布曲线。 中文名t 分布应用在对呈正态分布的总体 外文名t -distribution 别称学生 t 分布 学科概率论和统计学相关术语t 检验 目录 1历史 2定义 3扩展 4特征 5置信区间 6计算 历史 在概率论和统计学中,学生 t -分布( Student's t-distribution )经常应用在对呈正态分布的总体的均值进行估计。它是对两个样本均值差异进行显著性测试的学生t 测定的基础。 t 检定改进了Z 检定(en:Z-test ),不论样本数量大或小皆可应用。在样本数量大(超过 120 等)时,可以应用Z 检定,但 Z 检定用在小的样本会产生很大的误差,因此样本很小的情况下得改用学生t 检定。在数据有三组以上时,因为误差无法压低,此时可以用变异数分析代替学生t 检定。 当母群体的标准差是未知的但却又需要估计时,我们可以运用学生t-分布。 学生 t-分布可简称为t 分布。其推导由威廉·戈塞于 1908 年首先发表,当时他还在都柏林的健力士酿酒厂工作。因为不能以他本人的名义发表,所以论文使用了学生(Student )这一笔名。之后t 检验以及相关理论经由罗纳德·费雪的工作发扬光大,而正是他将此分布称为学生分布。 定义 标准正态分布表 x 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0 0.500 0 0.504 0 0.508 0 0.512 0 0.516 0 0.519 9 0.523 9 0.527 9 0.531 9 0.535 9 0.1 0.539 8 0.543 8 0.547 8 0.551 7 0.555 7 0.559 6 0.563 6 0.567 5 0.571 4 0.575 3 0.2 0.579 3 0.583 2 0.587 1 0.591 0 0.594 8 0.598 7 0.602 6 0.606 4 0.610 3 0.614 1 0.3 0.617 9 0.621 7 0.625 5 0.629 3 0.633 1 0.636 8 0.640 4 0.644 3 0.648 0 0.651 7 0.4 0.655 4 0.659 1 0.662 8 0.666 4 0.670 0 0.673 6 0.677 2 0.680 8 0.684 4 0.687 9 0.5 0.691 5 0.695 0 0.698 5 0.701 9 0.705 4 0.708 8 0.712 3 0.715 7 0.719 0 0.722 4 0.6 0.725 7 0.729 1 0.732 4 0.735 7 0.738 9 0.742 2 0.745 4 0.748 6 0.751 7 0.754 9 0.7 0.758 0 0.761 1 0.764 2 0.767 3 0.770 3 0.773 4 0.776 4 0.779 4 0.782 3 0.785 2 0.8 0.788 1 0.791 0 0.793 9 0.796 7 0.799 5 0.802 3 0.805 1 0.807 8 0.810 6 0.813 3 0.9 0.815 9 0.818 6 0.821 2 0.823 8 0.826 4 0.828 9 0.835 5 0.834 0 0.836 5 0.838 9 1 0.841 3 0.843 8 0.846 1 0.848 5 0.850 8 0.853 1 0.855 4 0.857 7 0.859 9 0.86 2 1 1.1 0.864 3 0.866 5 0.868 6 0.870 8 0.872 9 0.87 4 9 0.877 0 0.879 0 0.881 0 0.883 0 1.2 0.884 9 0.886 9 0.888 8 0.890 7 0.892 5 0.894 4 0.89 6 2 0.898 0 0.899 7 0.901 5 1.3 0.903 2 0.904 9 0.906 6 0.90 8 2 0.90 9 9 0.911 5 0.913 1 0.914 7 0.916 2 0.917 7 1.4 0.919 2 0.920 7 0.922 2 0.923 6 0.925 1 0.926 5 0.927 9 0.929 2 0.930 6 0.931 9 1.5 0.933 2 0.934 5 0.935 7 0.937 0 0.938 2 0.939 4 0.940 6 0.941 8 0.943 0 0.944 1 1.6 0.945 2 0.946 3 0.947 4 0.948 4 0.949 5 0.950 5 0.951 5 0.952 5 0.953 5 0.953 5 1.7 0.955 4 0.956 4 0.957 3 0.958 2 0.959 1 0.959 9 0.960 8 0.961 6 0.962 5 0.963 3 1.8 0.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0 0.970 6 1.9 0.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0 0.975 6 0.976 2 0.976 7 2 0.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.1 0.982 1 0.982 6 0.983 0 0.983 4 0.983 8 0.984 2 0.984 6 0.98 5 0 0.985 4 0.985 7 2.2 0.98 6 1 0.986 4 0.986 8 0.98 7 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.98 9 0 2.3 0.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.4 0.991 8 0.992 0 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.5 0.993 8 0.994 0 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.6 0.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0 0.996 1 0.996 2 0.996 3 0.996 4 2.7 0.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0 0.997 1 0.997 2 0.997 3 0.997 4 2.8 0.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0 0.998 1 2.9 0.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 3 0.998 7 0.999 0 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 0 2.4正态分布 复习引入: 总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线 b 单位 O 频率/组距 a 它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a,b)内取值的概率等于总体密度曲线,直线x=a,x=b及x轴所围图形的面积. 观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示: 2 2 () 2 , 1 (),(,) 2 x x e x μ σ μσ ? πσ - - =∈-∞+∞ 式中的实数μ、)0 (> σ σ是参数,分别表示总体的平均数与标准差,, ()x μσ ? 的图象为正态分布密度曲线,简称正态曲线. 讲解新课: 一般地,如果对于任何实数a b <,随机变量X 满足 ,()()b a P a X B x dx μσ?<≤=?, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2 σ μN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN . 经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位. 说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计. 2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布. 2.正态分布),(2 σ μN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响 标准正态分布 标准正态分布(英语:standard normal distribution,德语Standardnormalverteilung),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。期望值μ=0,即曲线图象对称轴为Y轴,标准差σ=1条件下的正态分布,记为N(0,1)。 定义: 标准正态分布又称为u分布,是以0为均数、以1为标准差的正态分布,记为N(0,1)。标准正态分布曲线下面积分布规律是:在-1.96~+1.96范围内曲线下的面积等于0.9500,在-2.58~+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表(自由度为∞时),借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。 正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数均数为0, 尺度参数:标准差为1的正态分布 特点: 密度函数关于平均值对称 平均值与它的众数(statistical mode)以及中位数(median)同一数值。 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。 95.449974%的面积在平均数左右两个标准差的范围内。 99.730020%的面积在平均数左右三个标准差的范围内。 99.993666%的面积在平均数左右四个标准差的范围内。 函数曲线的反曲点(inflection point)为离平均数一个标准差距离的位置。 标准偏差: 深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中,此范围所占比率为全部数值之68%,根据正态分布,两个标准差之内的比率合起来为95%;三个标准差之内的比率合起来为99%。 在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则” 附表1. 标准正态分布表 x0.000.010.020.030.040.050.060.070.080.09 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.90.500 0 0.539 8 0.579 3 0.617 9 0.655 4 0.691 5 0.725 7 0.758 0 0.788 1 0.815 9 0.841 3 0.864 3 0.884 9 0.903 2 0.919 2 0.933 2 0.945 2 0.955 4 0.964 1 0.971 3 0.977 2 0.982 1 0.986 1 0.989 3 0.991 8 0.993 8 0.995 3 0.996 5 0.997 4 0.998 1 0.504 0 0.543 8 0.583 2 0.621 7 0.659 1 0.695 0 0.729 1 0.761 1 0.791 0 0.818 6 0.843 8 0.866 5 0.886 9 0.904 9 0.920 7 0.934 5 0.946 3 0.956 4 0.964 8 0.971 9 0.977 8 0.982 6 0.986 4 0.989 6 0.992 0 0.994 0 0.995 5 0.996 6 0.997 5 0.998 2 0.508 0 0.547 8 0.587 1 0.625 5 0.662 8 0.698 5 0.732 4 0.764 2 0.793 9 0.821 2 0.846 1 0.868 6 0.888 8 0.906 6 0.922 2 0.935 7 0.947 4 0.957 3 0.965 6 0.972 6 0.978 3 0.983 0 0.986 8 0.989 8 0.992 2 0.994 1 0.995 6 0.996 7 0.997 6 0.998 2 0.512 0 0.551 7 0.591 0 0.629 3 0.666 4 0.701 9 0.735 7 0.767 3 0.796 7 0.823 8 0.848 5 0.870 8 0.890 7 0.908 2 0.923 6 0.937 0 0.948 4 0.958 2 0.966 4 0.973 2 0.978 8 0.983 4 0.987 1 0.990 1 0.992 5 0.994 3 0.995 7 0.996 8 0.997 7 0.998 3 0.516 0 0.555 7 0.594 8 0.633 1 0.670 0 0.705 4 0.738 9 0.770 3 0.799 5 0.826 4 0.850 8 0.872 9 0.892 5 0.909 9 0.925 1 0.938 2 0.949 5 0.959 1 0.967 2 0.973 8 0.979 3 0.983 8 0.987 4 0.990 4 0.992 7 0.994 5 0.995 9 0.996 9 0.997 7 0.998 4 0.519 9 0.559 6 0.598 7 0.636 8 0.673 6 0.708 8 0.742 2 0.773 4 0.802 3 0.828 9 0.853 1 0.874 9 0.894 4 0.911 5 0.926 5 0.939 4 0.950 5 0.959 9 0.967 8 0.974 4 0.979 8 0.984 2 0.987 8 0.990 6 0.992 9 0.994 6 0.996 0 0.997 0 0.997 8 0.998 4 0.523 9 0.563 6 0.602 6 0.640 4 0.677 2 0.712 3 0.745 4 0.776 4 0.805 1 0.835 5 0.855 4 0.877 0 0.896 2 0.913 1 0.927 9 0.940 6 0.951 5 0.960 8 0.968 6 0.975 0 0.980 3 0.984 6 0.988 1 0.990 9 0.993 1 0.994 8 0.996 1 0.997 1 0.997 9 0.998 5 0.527 9 0.567 5 0.606 4 0.644 3 0.680 8 0.715 7 0.748 6 0.779 4 0.807 8 0.834 0 0.857 7 0.879 0 0.898 0 0.914 7 0.929 2 0.941 8 0.952 5 0.961 6 0.969 3 0.975 6 0.980 8 0.985 0 0.988 4 0.991 1 0.993 2 0.994 9 0.996 2 0.997 2 0.997 9 0.998 5 0.531 9 0.571 4 0.610 3 0.648 0 0.684 4 0.719 0 0.751 7 0.782 3 0.810 6 0.836 5 0.859 9 0.881 0 0.899 7 0.916 2 0.930 6 0.943 0 0.953 5 0.962 5 0.970 0 0.976 2 0.981 2 0.985 4 0.988 7 0.991 3 0.993 4 0.995 1 0.996 3 0.997 3 0.998 0 0.998 6 0.535 9 0.575 3 0.614 1 0.651 7 0.687 9 0.722 4 0.754 9 0.785 2 0.813 3 0.838 9 0.862 1 0.883 0 0.901 5 0.917 7 0.931 9 0.944 1 0.953 5 0.963 3 0.970 6 0.976 7 0.981 7 0.985 7 0.989 0 0.991 6 0.993 6 0.995 2 0.996 4 0.997 4 0.998 1 0.998 6 x0.00.10.20.30.40.50.60.70.80.9 30.998 70.999 00.999 30.999 50.999 70.999 80.999 80.999 90.999 9 1.000 0 若n个相互独立的随机变量ξ?,ξ?,...,ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。 目录 1简介 2定义 3性质 4概率表 简介 分布在数理统计中具有重要意义。分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。 定义 若n个相互独立的随机变量ξ?、ξ?、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为分布(chi-square distribution), 卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。 对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。 性质 1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数 的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。 2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。 3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。 4) 若互相独立,则:服从分布,自由度为 。 5) 分布的均数为自由度,记为 E( ) = 。 6) 分布的方差为2倍的自由度( ),记为 D( ) = 。 概率表 分布不象正态分布那样将所有正态分布的查表都转化为标准正态分布去查,在 分布中得对每个分布编制相应的概率值,这通过分布表中列出不同的自由度来表示, 查分布概率表时,按自由度及相应的概率去找到对应的值。如上图所示的单侧概率(7)=的查表方法就是,在第一列找到自由度7这一行,在第一行中找到概率这一列,行列的交叉处即是。 表中所给值直接只能查单侧概率值,可以变化一下来查双侧概率值。例如,要在自由度为7的卡方分布中,得到双侧概率为所对应的上下端点可以这样来考虑:双侧概率指的是在 正态分布 1.关于正态分布N (μ,σ2),下列说法正确的是( ) A .随机变量落在区间长度为3σ的区间之外是一个小概率事件 B .随机变量落在区间长度为6σ的区间之外是一个小概率事件 C .随机变量落在(-3σ,3σ)之外是一个小概率事件 D .随机变量落在(μ-3σ,μ+3σ)之外是一个小概率事件 2.已知随机变量ξ服从正态分布N (4,σ2),则P (ξ>4)=( ) A.15 B .14 C.13 D .12 3.若随机变量X 的密度函数为f (x )=12π·e -x 22,X 在区间(-2,-1)和(1,2)内取值的概率分别为p 1,p 2,则p 1,p 2的关系为( ) A .p 1>p 2 B .p 1 c )=p ,则p 的值为( ) A .0 B .0.5 C .1 D .不确定 9.已知随机变量X ~N (0,σ2).若P (X >2)=0.023,则P (-2≤X ≤2)=( ) A .0.477 B .0.628 C .0.954 D .0.977 10.某地区高二女生的体重X (单位:kg)服从正态分布N (50,25),若该地区共有高二女生2 000人,则体重在50 kg ~65 kg 间的女生共有( ) A .683人 B .954人 C .997人 D .994人 11.图是三个正态分布X ~N (0,0.25),Y ~N (0,1),Z ~N (0,4)的密度曲线,则三个随机变量X ,Y ,Z 对应曲线分别是图中的________、________、________. 12.设随机变量ξ服从正态分布N (2,9),若P (ξ>c +1)=P (ξ 正态分布 以平均值为中心呈对称分布的钟形曲线。正态分布是最常见的统计分布,因为许多物理、生物和社会方面的测量值都自然近似于正态。许多统计分析均要求数据来自正态分布总 体。 例如,居住在宾夕法尼亚州的所有成年男性的身高近似于正态分布。因此,大多数男性的身高都将接近于 69 英寸的平均身高。高于和矮于 69 英寸的男性的数量相近。只有一小部分身材特别高或特别矮。 平均值 (μ) 和标准差 (σ) 是定义正态分布的两种参数。平均值是钟形曲线的波峰或中心。标准差决定数据的散布情况。大约有 68% 的观测值与平均值相差不到 +/- 1 个标准差;95% 与平均值相差不到 +/- 2 个标准差;而 99% 的观测值与平均值相差不到 +/- 3 个标准差。 就宾夕法尼亚州男性的身高而言,平均身高为 69 英寸,标准差为 2.5 英寸。 大约68% 的宾夕法尼亚男性身高介于66.5 (μ- 1σ) 和71.5 (μ+ 1σ) 英寸之间。 大约95% 的宾夕法尼亚男性身高介于64 (μ- 2σ) 和74 (μ+ 2σ) 英寸之间。 大约99% 的宾夕法尼亚男性身高介于61.5 (μ- 3σ) 和76.5 (μ+ 3σ) 英寸之间。 过程能力 生产或提供满足根据客户需要定义的规格的产品或服务的能力。例如,影印机制造商要求橡胶辊筒的宽度必须介于 32.523 cm 与 32.527 cm 之间,才能避免卡纸。能力分析揭示了制造过程满足这些规格的程度,并提供有关如何改进该过程和维持改进的见解。 在评估过程能力之前,必须确保过程是稳定的。不稳定的过程是无法预测的。如果过程稳定,则可以预测将来的性能并改进其能力。 应定期测量并分析过程的能力。能力分析有助于回答以下问题: ?过程是否满足客户规格? ?过程将来的性能如何? ?过程是否需要改进? ?过程是保持了这些改进还是回复到了原来的未改进状态? 可使用过程指标(如 Cp、Pp、Cpk 和 Ppk)来分析过程能力。 潜在(组内)能力和整体能力 大多数能力评估都可以分组为两种类别中的一种:潜在(组内)能力和整体能力。每种能力都表示对过程能力的唯一度量。潜在能力通常称为过程的“权利”:它忽略子组之间的差异并表示当消除了子组之间的偏移和漂移时执行过程的方法。另一方面,整体能力是客户所体验到的;它考虑了子组之间的差异。评估潜在能力的能力指标包括 Cp、CPU、CPL 和 Cpk。评估整体能力的能力指标包括 Pp、PPU、PPL、Ppk 和 Cpm。 例如,您检查某一糖果厂的设备,其中包括将特定重量的糖果装入容器的机器。糖果每周从工厂出货一次。为评估此过程的能力,在一周内的每天,对袋子样本进行称重;每个样本在分析中表示一个子组。观察发现,每个子组内的变异性很小,但由于子组平均值每天都有偏移,因此袋子重量的总体变异性很大。因此,整个一周的出货在袋子重量上与给定日期内生产的袋子重量之间存在较大的变异性。在下图中,较小的分布表示连续七天内每天的袋子重量的分布。最上面的分布表示整周的出货,它是子组的合计。 标准正态分布表 0.000.010.020.030.040.050.060.070.080.09 0.00.50000.50400.50800.51200.51600.51990.52390.52790.53190.5359 0.10.53980.54380.54780.55170.55570.55960.56360.56750.57140.5753 0.20.57930.58320.58710.59100.59480.59870.60260.60640.61030.6141 0.30.61790.62170.62550.62930.63310.63680.64060.64430.64800.6517 0.40.65540.65910.66280.66640.67000.67360.67720.68080.68440.6879 0.50.69150.69500.69850.70190.70540.70880.71230.71570.71900.7224 0.60.72570.72910.73240.73570.73890.74220.74540.74860.75170.7549 0.70.75800.76110.76420.76730.77040.77340.77640.77940.78230.7852 0.80.78810.79100.79390.79670.79950.80230.80510.80780.81060.8133 0.90.81590.81860.82120.82380.82640.82890.83150.83400.83650.8389 1.00.84130.84380.84610.84850.85080.85310.85540.85770.85990.8621 1.10.86430.86650.86860.87080.87290.87490.87700.87900.88100.8830 1.20.88490.88690.88880.89070.89250.89440.89620.89800.89970.9015 1.30.90320.90490.90660.90820.90990.91150.91310.91470.91620.9177 1.40.91920.92070.92220.92360.92510.92650.92790.92920.93060.9319 1.50.93320.93450.93570.93700.93820.93940.94060.94180.94290.9441 1.60.94520.94630.94740.94840.94950.95050.95150.95250.95350.9545 1.70.95540.95640.95730.95820.95910.95990.96080.96160.96250.9633 1.80.96410.96490.96560.96640.96710.96780.96860.96930.96990.9706 1.90.97130.97190.97260.97320.97380.97440.97500.97560.97610.9767 2.00.97720.97780.97830.97880.97930.97980.98030.98080.98120.9817 2.10.98210.98260.98300.98340.98380.98420.98460.98500.98540.9857 2.20.98610.98640.98680.98710.98750.98780.98810.98840.98870.9890 2.30.98930.98960.98980.99010.99040.99060.99090.99110.99130.9916 2.40.99180.99200.99220.99250.99270.99290.99310.99320.99340.9936 2.50.99380.99400.99410.99430.99450.99460.99480.99490.99510.9952 2.60.99530.99550.99560.99570.99590.99600.99610.99620.99630.9964 2.70.99650.99660.99670.99680.99690.99700.99710.99720.99730.9974 2.80.99740.99750.99760.99770.99770.99780.99790.99790.99800.9981 2.90.99810.99820.99820.99830.99840.99840.99850.99850.99860.9986 3.00.99870.99870.99870.99880.99880.99890.99890.99890.99900.9990 标准正态分布表 就力二「冷=亡P(X 正态分布概率表 0( u ) t F(t)t F(0t F( t)t F(t) 0+00O.COOO0,230.181 90,460.354 50.690.509 8 0.010.008 00.24o, m70.470,361 60J00.516 1 0+020.016 00,250,197 40,480.368 80+710,522 3 0+030023 90 260.205 10,490.375 91720.528 5 0.04 C.031 90.270.212 80.500.382 90.730.534 6 0.050+039 90.280.220 50.510.389 90.740.540 7 0.060.047 80 290. 22S 20.520.396 90.750.546 7 0,070,055 S0. 300.235 80.530.403 90.760.552 7 0.0S0.063 8(1. 310.243 40.540.410 80.770.558 7 0 + 090.071 7C,320.251 00&0.417 70+780.564 6 (k 1U0079 7(J. 330.258 60.560.424 50+790.570 5 0.11O.fi87 6 C. 340.266 10.570.431 3o.so0, 57 6 3 4 120.09 5 50 350.273 70,5S0,43S 1 0.S10.582 1 A130.103 1 C. 360.281 20.590.444 80,820.587 8 0.140,111 30. 370.288 60.600.451 50.S30.593 5 0+150.119 20.380,29 6 10.610.458 1 (U40*599 1 0.160,12 7 ] 0.390, 303 50.620.464 70.350,604 7 0.170 135 0G.400310 80.630.471 30, R60.6102 0.180J42 S0.410.31 8 20.640.477 S0+870,15 7 0.190.150 70 420325 50.650.484 30+880.621 1 0.200.158 50.430. 332 80.660.490 70.890 . 62 6 5 0,210J66 3C,440.340 10.670.497 1 0.900.631 9 A 220.174 ] 0.45(L 347 30.680.503 50.910.637 2 正态分布 (normal distribution ) 一、 定义 如果连续型随机变量取值分布呈现单峰、对称、两侧均匀变动的钟 形分布,且能用下列函数描述其位置和形状特征的,则称之为正态分布。 概率密度函数 , -∞ 四、 应用 1、描述资料分布 2、依据面积分布规律求医学参考值范围 3、质量控制方法中随机误差分布符合正态,可用一定范围作为质量警戒线和 控线 4、标准正态分布的U 值,可视为重要统计量,是大样本参数估计和假设检验 的基础。而且用于求资料某一定范围内分布的理论频数(n 、x 、s )已计算出 例:已知x =50,S=10,N=200,求45 正态分布的前世今生 【德国马克上的高斯头像和正态分布曲线】 正态曲线虽然看上去很美,却不是一拍脑袋就能想到的。我们在本科学习数理统计的 时候,课本一上来介绍正态分布就给出密度分布函数,却从来不说明这个分布函数是通过 什么原理推导出来的。所以我一直搞不明白数学家当年是怎么找到这个概率分布曲线的, 又是怎么发现随机误差服从这个奇妙的分布的。我们在实践中大量的使用正态分布,却对 这个分布的来龙去脉知之甚少,正态分布真是让人感觉既熟悉又陌生。直到我读研究生的 时候,我的导师给我介绍了陈希儒院士的《数理统计学简史》这本书,看了之后才了解了 正态分布曲线从发现到被人们重视进而广泛应用,也是经过了几百年的历史。 正态分布的这段历史是很精彩的,我们通过讲一系列的故事来揭开她的神秘面纱。标准正态分布表
(完整版)t分布的概念及表和查表方法.doc
标准正态分布表
正态分布讲解(含标准表)
标准正态分布
标准正态分布查询表
卡方分布概念及表和查表方法
正态分布
正态分布分析
标准正态分布表
标准正态分布表
正态分布
正态分布的前世今生(完整版)
一、正态分布,熟悉的陌生人
学过基础统计学的同学大都对正态分布非常熟悉。这个钟型的分布曲线不但形状优雅, 其密度函数写成数学表达式
12π??√σexp(?(x?μ)22σ2)
也非常具有数学的美感。其标准化后的概率密度函数
12π??√exp(?x22) 更加的简洁漂亮,两个最重要的数学常量 π,e 都出现在了公式之中。在我个人的审美之中,
它也属于 top-N 的最美丽的数学公式之一, 如果有人问我数理统计领域哪个公式最能让人感觉 到上帝的存在,那我一定投正态分布的票。因为这个分布戴着神秘的面纱,在自然界中无处不 在,让你在纷繁芜杂的数据背后看到隐隐的秩序。
【正态分布曲线】
正态分布又通常被称为高斯分布,在科学领域,冠名权那是一个很高的荣誉。早年去 过德国的兄弟们还会发现,德国的钢镚和 10 马克的纸币上都留有高斯的头像和正态密度 曲线。正态分布被冠名高斯分布,我们也容易认为是高斯发现了正态分布,其实不然,不 过高斯对于正态分布的历史地位的确立是起到了决定性的作用。
1
二、邂逅,正态曲线的首次发现
第一个故事和概率论的发展密切相关,主角是棣莫弗(De Moivre)和拉普拉斯 (Laplace)。拉普拉斯是个大科学家,被称为法国的牛顿;棣莫弗名气可能不算很大,不 过大家应该都熟悉这个名字,因为我们在高中数学学复数的时候我们都学过棣莫弗定理
(cosθ+isinθ)n=cos(nθ)+isin(nθ). 古典概率论发源于赌博,惠更斯、帕斯卡、费马、贝努利都是古典概率的奠基人,他们那
会研究的概率问题大都来自赌桌上,最早的概率论问题是赌徒梅累在 1654 年向帕斯卡提出的 如何分赌金的问题。 统计学中的总体均值之所以被称为期望(Expectation), 就是源自惠更斯、 帕斯卡这些人研究平均情况下一个赌徒在赌桌上可以期望自己赢得多少钱。
棣莫弗(De Moivre)
拉普拉斯 (Laplace)
2
