您的位置：360文档中心› 正态分布及其经典习题和答案44733

正态分布及其经典习题和答案44733

正态分布及其经典习题和答案44733

正态分布及其经典习题和答案44733

专题：正态分布

例：（1）已知随机变量X 服从二项分布，且E （X ）=，V （X ）=，则二项分布的参数n ，p 的值为 A ．n=4，p=

B ．n=6,p=

C ．n=8，p=

D ．n=24，p=

答案：B 。解析：()4.2==np X E ，()44.1)1(=-=p np X V 。

（2）正态曲线下、横轴上，从均数到∞+的面积为( )。

A ．95%

B ．50%

C ．%

D ．不能确定（与标准差的大小有关）答案：B 。解析：由正态曲线的特点知。

（3）某班有48名同学，一次考试后的数学成绩服从正态分布，平均分为80，标准差为10，理论上说在80分到90分的人数是

（）

A 32

B 16

C 8

D 20 答案：B 。解析:数学成绩是X —N(80,102)，

80809080(8090)(01)0.3413,480.3413161010P X P Z P Z --??≤≤=≤≤=≤≤≈?≈ ???

。（4）从1，2，3，4，5这五个数中任取两个数，这两个数之积的数学期望为___________ 。

答案：。解析：设两数之积为X ，

∴E(X)=.

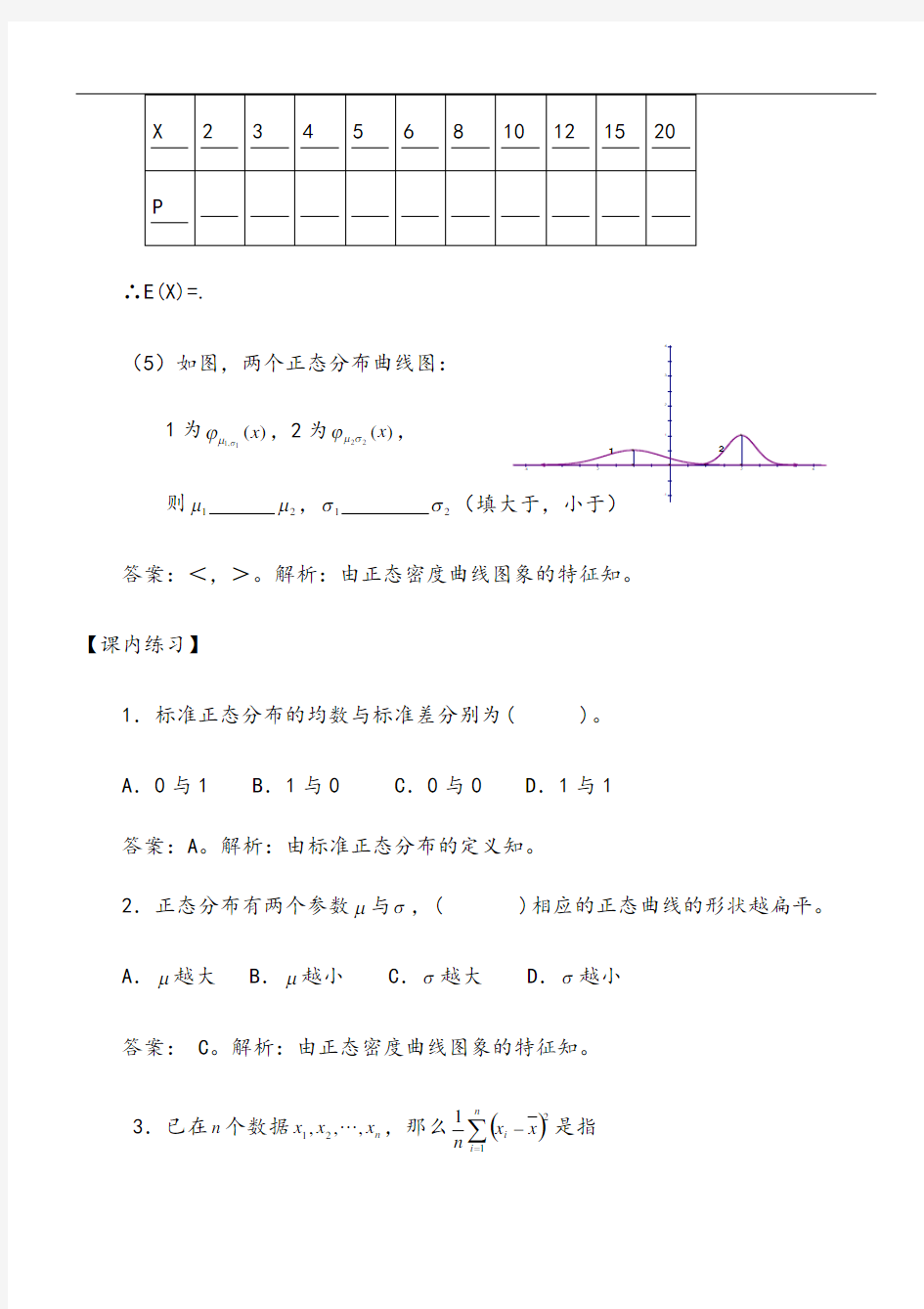
（5）如图，两个正态分布曲线图：

1为)(1

,1x σμ?，2为)(2

2

x σμ?，

则1μ 2μ，1σ 2σ答案：＜，＞。解析：由正态密度曲线图象的特征知。【课内练习】

1．标准正态分布的均数与标准差分别为( )。 A ．0与1 B ．1与0 C ．0与0 D ．1与1 答案：A 。解析：由标准正态分布的定义知。

2．正态分布有两个参数μ与σ，( )相应的正态曲线的形状越扁平。 A ．μ越大 B ．μ越小 C ．σ越大 D ．σ越小答案： C 。解析：由正态密度曲线图象的特征知。

3．已在n 个数据n x x x ,,,21 ，那么()

∑=-n

i i x x n 1

21是指

A ．σ

B ．μ

C ．2σ

D ．2μ（）答案：C 。解析：由方差的统计定义知。

4．设),(~p n B ξ，()12=ξE ，()4D ξ=，则n 的值是。答案：4。解析：()12==np E ξ，()(1)4D np p ξ=-=

5．对某个数学题，甲解出的概率为23

，乙解出的概率为34

，两人独立解题。记X

为解出该题的人数，则E （X ）= 。

答案：1712

。解析：11121145(0),(1),34

12343412P X P X ==?=

==?+?=231(2)342

P X ==?=。 ∴15

117

()0122

12

212

E X =?+?+?

=。 6．设随机变量ξ服从正态分布)1,0(N ，则下列结论正确的是。 (1))0)(|(|)|(|)|(|>=+<=-<=<-=>-=

答案：(1),(2),(4)。解析：(||)0P a ξ==。

7．抛掷一颗骰子，设所得点数为X ，则D （X ）= 。答案：3512

。解析：1(),1,2,

P X k k ===，按定义计算得735

。【作业本】 A 组

1．袋中装有5只球，编号为1，2，3，4，5，从中任取3球，以X 表示取出球的

答案：C 。解析：X 的分布列为

故E （X ）=?+?+?=。 2

22)(x e x f -=π

221)(x e x f π

答案：B 。解析：选项B 是标准正态分布密度函数。

3．正态总体为1,0-==σμ概率密度函数)(x f 是（） A ．奇函数 B ．偶函数 C ．非奇非偶函数 D ．既是奇函数又是偶函数答案：B 。解析：2

4．已知正态总体落在区间()+∞,2.0的概率是0．5，那么相应的正态曲线在=x

时达到最高点。

答案：。解析：正态曲线关于直线x μ=对称，由题意知0.2μ=。

5．一次英语测验由40道选择题构成，每道有4个选项，其中有且仅有一个是正确的，每个选对得3分，选错或不选均不得分，满分120分，某学生选对一道题的概率为，求该生在这次测验中的成绩的期望为；方差为。

答案：84；。解析：设X 为该生选对试题个数，η为成绩，则X ～B （50，），η=3X ∴E(X)=40×=28 V(X)=40××=

故E(η)=E(3X)=3E(X)=84 V(η)=V(3X)=9V(X)=

6．某人进行一个试验，若试验成功则停止，若实验失败，再重新试验一次，若试验三次均失败，则放弃试验，若此人每次试验成功的概率为3

，求此人试验次数X 的分布列及期望和方差。

解：X 的分布列为

E X =?+?+?=，22211338()149()3

V X =?+?+?-=。

7．甲、乙两名射击运动员，甲射击一次命中10环的概率为，乙射击一次命中10环的概率为s ，若他们独立的射击两次，设乙命中10环的次数为X ，则EX=3

为甲与乙命中10环的差的绝对值.求s 的值及Y 的分布列及期望. 答案：解：由已知可得),2(~s B X ，故3

42===s s EX 所以．有Y 的取值可以是0，1，2.

甲、乙两人命中10环的次数都是0次的概率是36

?，甲、乙两人命中10环的次数都是1次的概率是9

132)(21212121(=?+??+?，甲、乙两人命中10环的次数都是2次的概率是9

1)3232)(2121(=?? 所以36

=Y P ；甲命中10环的次数是2且乙命中10环的次数是0次的概率是36

?，甲命中10环的次数是0且乙命中10环的次数是2次的概率是9

?? 所以36591361)2(=

)2()0(1)1(==-=-==Y P Y P Y P 所以Y 的分布列是

所以 Y 的期望是E （Y ）=9

1．某产品的废品率为，从中取出10个产品，其中的次品数X 的方差是（）

答案：B 。解析：X —B （10，），()100.050.950.475V X =??=。 2．若正态分布密度函数()2

∈，下列判断正确的是（）

A ．有最大值，也有最小值

B ．有最大值，但没最小值

C ．有最大值，但没最大值

D ．无最大值和最小值答案：B 。

3．在一次英语考试中，考试的成绩服从正态分布)36,100(，那么考试成绩在区间(]112,88内的概率是

D ．0．9974 答案：C 。解析：由已知X —N （100，36），

故88100112100(88112)()(22)2(2)10.95446

P X P Z P Z P Z --<≤=<≤=-<≤=≤-=。

4．袋中有4个黑球，3个白球，2个红球，从中任取2个球，每取到一个黑球得0分，每取到一个白球得1分，若取到一个红球则得2分，用X 表示得分数，则E （X ）=________；D(X)= _________.

。解析：由题意知，X 可取值是0，1，2，3，4。易得其概率分布如下：

1136＋3×16＋4×136＝14

V(X)= 20×16+21×13＋22×1136＋23×16＋24×136－2

162165 注：要求次品数的数学期望与方差，应先列出次品数X 的分布列。 5．若随机变量X 的概率分布密度函数是())(,221)(8

答案：-5。解析：2,2,(21)2()12(2)15E X E X σμ==--=-=?--=-。

6．一本书有500页，共有100个错字，随机分布在任意一页上，求一页上错字个数X 的均值、标准差。

解：∵X —B 1111

(100,),()1000.2,()100(1)0.1996500500500500

E X V X ∴=?==??-= X 的标准差

8．一批电池（一节）用于手电筒的寿命服从均值为小时、标准差为小时的正态分布，随机从这批电池中任意取一节，问这节电池可持续使用不少于40小时的概率是多少

答案：解：电池的使用寿命X —N,

则35.64035.6(40)()(1)1(1)0.15874.4

X P X P P Z P Z --≥=≥=≥=-≤=

即这节电池可持续使用不少于40小时的概率是。正态分布双基自测

1．设有一正态总体，它的概率密度曲线是函数f (x )的图象，且f (x )＝1

，则这个正态总体的平均数与标准差分别是( )．

D ．2与10 解析由1

，可知σ＝2，μ＝10.答案

2．(2011·湖北)已知随机变量ξ服从正态分布N (2，σ2)，且P (ξ＜4)＝，则P (0＜ξ＜2)等于( )．

解析由P (ξ＜4)＝知P (ξ＞4)＝P (ξ＜0)＝，故P (0＜ξ＜2)＝.故选C.答案 C

3．(2010·广东)已知随机变量X 服从正态分布N (3,1)，且P (2≤X ≤4)＝ 6，则P (X ＞4)等于( )．

解析由正态曲线性质知，其图象关于直线x ＝3对称，∴P (X ＞4)＝－1

2P (2≤X ≤4)

× 6＝ 7.故选B

4．(2010·山东)已知随机变量X 服从正态分布N (0，σ2)，若P (X >2)＝，则P (－2≤X ≤2)等于( )．

D ．解析 P (－2≤X ≤2)＝1－2P (X >2)＝.答案 C

5．设随机变量X 服从正态分布N (2,9)，若P (X >c ＋1)＝P (X

∵μ＝2，由正态分布的定义知其函数图象关于x ＝2对称，于是c ＋1＋c －1

∴c ＝2.答案 B

考向一正态曲线的性质

【例1】?若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值为1

(1)求该正态分布的概率密度函数的解析式； (2)求正态总体在(－4,4]的概率．

解 (1)由于该正态分布的概率密度函数是一个偶函数，所以其图象关于y 轴对称，即μ＝0.由12πσ＝1

，得σ＝4，故该正态分布的概率密度函数的解析式

是φμ，σ(x )＝142πe －x 2

，x ∈(－∞，＋∞)．

【训练1】设两个正态分布N (μ1，σ21)(σ1＞0)和N (μ2，σ2

2)(σ2＞0)的密度函数

图象如图所示，则有( )． A ．μ1＜μ2，σ1＜σ2 B ．μ1＜μ2，σ1＞σ2 C ．μ1＞μ2，σ1＜σ2 D ．μ1＞μ2，σ1＞σ2

解析根据正态分布N (μ，σ2)函数的性质：正态分布曲线是一条关于直线x ＝μ对称，在x ＝μ处取得最大值的连续钟形曲线；σ越大，曲线的最高点越低且较平缓；反过来，σ越小，曲线的最高点越高且较陡峭，故选A. 考向二服从正态分布的概率计算【例2】?设X ～N (1,22)，试求

× 4－ 6)＝ 9.

(3)∵P(X≥5)＝P(X≤－3)，∴P(X≥5)＝1

[1－P(μ－2σ

×(1－ 4)＝ 8.

【训练2】随机变量ξ服从正态分布N(1，σ2)，已知P(ξ＜0)＝，则P(ξ＜2)＝________.

解析由题意可知，正态分布的图象关于直线x＝1对称，所以P(ξ＞2)＝P(ξ＜0)＝，P(ξ＜2)＝1－＝.答案

考向三正态分布的应用

【例3】?2011年中国汽车销售量达到1 700万辆，汽车耗油量对汽车的销售有着非常重要的影响，各个汽车制造企业积极采用新技术降低耗油量，某汽车制造公司为调查某种型号的汽车的耗油情况，共抽查了1 200名车主，据统计该种型号的汽车的平均耗油为百公里升，并且汽车的耗油量ξ服从正态分布N(8，σ2)，已知耗油量ξ∈[7,9]的概率为，那么耗油量大于9升的汽车大约有________辆．

解由题意可知ξ～N(8，σ2)，故正态分布曲线以μ＝8为对称轴，又因为P(7≤ξ≤9)＝，故P(7≤ξ≤9)＝2P(8≤ξ≤9)＝，所以P(8≤ξ≤9)＝，而P(ξ≥8)＝，所以P(ξ＞9)＝，故耗油量大于9升的汽车大约有1 200×＝180辆．

【训练3】工厂制造的某机械零件尺寸X 服从正态分布N ?

4，19，问在一次正常的试

验中，取1 000个零件时，不属于区间(3,5]这个尺寸范围的零件大约有多少个

解 ∵X ～N ?

????4，19，∴μ＝4，σ＝1

3.∴不属于区间(3,5]的概率为

P (X ≤3)＋P (X ＞5)＝1－P (3＜X ≤5)＝1－P (4－1＜X ≤4＋1)＝1－P (μ－3σ＜X ≤μ＋3σ)

＝1－ 4＝ 6≈，∴1 000×＝3(个)，

即不属于区间(3,5]这个尺寸范围的零件大约有3个．阅卷报告19——正态分布中概率计算错误

【问题诊断】正态分布是高中阶段唯一连续型随机变量的分布，这个考点虽然不是高考的重点，但在近几年新课标高考中多次出现，其中数值计算是考查的一个热点，考生往往不注意对这些数值的记忆而导致解题无从下手或计算错误．

【防范措施】对正态分布N (μ，σ2)中两个参数对应的数值及其意义应该理解透彻并记住，且注意第二个数值应该为σ2而不是σ，同时，记住正态密度曲线的六条性质．

【示例】? 已知某次数学考试的成绩服从正态分布N (116，64)，则成绩在140分以上的考生所占的百分比为

错因 (1)不能正确得出该正态分布的两个参数μ，σ导致计算无从下手．(2)对正态分布中随机变量在三个区间内取值的概率数值记忆不准，导致计算出错．

实录同学甲 A 同学乙 B 同学丙 C

正解依题意，μ＝116，σ＝8，所以μ－3σ＝92，μ＋3σ＝140，而服从正态分布的随机变量在(μ－3σ，μ＋3σ)内取值的概率约为，所以成绩在区间(92,140)内的考生所占百分比约为%，从而成绩在140分以上的考生所占的百分比为1－%

【试一试】在正态分布N ?

0，19中，数值落在(－∞，－1)∪(1，＋∞)内的概率为

解析 ∵μ＝0，σ＝1

3，∴P (x ＜－1或x ＞1)＝1－P (－1≤x ≤1)＝1－P (μ－

3σ≤x ≤μ＋3σ)＝1－ 4＝ 6. 答案 D

一元二次方程应用题经典题型汇总含答案

z一元二次方程应用题经典题型汇总一、增长率问题例1　恒利商厦九月份的销售额为200万元，十月份的销售额下降了20%，商厦从十一月份起加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了193.6万元，求这两个月的平均增长率. 解　设这两个月的平均增长率是x.，则根据题意，得200(1－20%) (1+x)2＝193.6，即(1+x)2＝1.21，解这个方程，得x1＝0.1，x2＝－2.1（舍去）. 答　这两个月的平均增长率是10%. 说明　这是一道正增长率问题，对于正的增长率问题，在弄清楚增长的次数和问题中每一个数据的意义，即可利用公式m(1+x)2＝n求解，其中m＜n.对于负的增长率问题，若经过两次相等下降后，则有公式m(1－x)2＝n即可求解，其中m＞n. 二、商品定价例2　益群精品店以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品售价a元，则可卖出（350－10a）件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400元，需要进货多少件？每件商品应定价多少？解　根据题意，得(a－21)(350－10a)＝400，整理，得a2－56a+775＝0，解这个方程，得a1＝25，a2＝31. 因为21×(1+20%)＝25.2，所以a2=31不合题意，舍去. 所以350－10a＝350－10×25＝100（件）. 答　需要进货100件，每件商品应定价25元. 说明　商品的定价问题是商品交易中的重要问题，也是各种考试的热点.

三、储蓄问题例3　王红梅同学将1000元压岁钱第一次按一年定期含蓄存入“少儿银行”，到期后将本金和利息取出，并将其中的500元捐给“希望工程”，剩余的又全部按一年定期存入，这时存款的年利率已下调到第一次存款时年利率的90%，这样到期后，可得本金和利息共530元，求第一次存款时的年利率.（假设不计利息税）解　设第一次存款时的年利率为x. 则根据题意，得[1000(1+x)－500](1+0.9x)＝530.整理，得 90x2+145x－3＝0. 解这个方程，得x1≈0.0204＝2.04%，x2≈－1.63.由于存款利率不能为负数，所以将x2≈－1.63舍去. 答　第一次存款的年利率约是2.04%. 说明　这里是按教育储蓄求解的，应注意不计利息税. 四、趣味问题例4　一个醉汉拿着一根竹竿进城，横着怎么也拿不进去，量竹竿长比城门宽4米，旁边一个醉汉嘲笑他，你没看城门高吗，竖着拿就可以进去啦，结果竖着比城门高2米，二人没办法，只好请教聪明人，聪明人教他们二人沿着门的对角斜着拿，二人一试，不多不少刚好进城，你知道竹竿有多长吗？解　设渠道的深度为xm，那么渠底宽为(x+0.1)m，上口宽为 (x+0.1+1.4)m. 则根据题意，得 (x+0.1+x+1.4+0.1)·x＝1.8，整理，得x2+0.8x－1.8＝0. 解这个方程，得x1＝－1.8（舍去），x2＝1. 所以x+1.4+0.1＝1+1.4+0.1＝2.5. 答　渠道的上口宽2.5m，渠深1m.

随机变量及其分布列经典例题

随机变量及其分布列典型例题【知识梳理】一.离散型随机变量的定义 1定义:在随机试验中,确定一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果变化而变化的变量称为随机变量、 ①随机变量就是一种对应关系;②实验结果必须与数字对应; ③数字会随着实验结果的变化而变化、 2.表示:随机变量常用字母X ,Ｙ,ξ,η,…表示. 3、所有取值可以一一列出的随机变量,称为离散型随机变量 ( dis ｃｒe ｔｅｒan ｄｏm ｖar ｉa ｂle ) . 二、离散型随机变量的分布列 1.一般地,若离散型随机变量X 可能取的不同值为x 1,x 2,…,ｘi ,…,x n, X 取每一个值x i (ｉ=1,2,…, ｎ)的概率P (X =ｘｉ)=ｐi ,则称表: 为离散型随机变量X Ｐ(X =x i )＝p i , i =１,２,…,n, 也可以用图象来表示X 的分布列、 2.离散型随机变量的分布列的性质 ①ｐi ≥0,ｉ=１,2,…,n ;②11 =∑=n i i p . 三.两个特殊分布 1.两点分布),1(~P B X 若随机变量X 的分布列具有上表形式,则称服从两点分布,并称p =P (X ＝1)为成功概率. 2、超几何分布),,(~n M N H X 一般地,在含有M 件次品的N 件产品中,任取ｎ件,其中恰有X 件次品,则P (X ＝k )= n N k n M N k M C C C --,k =0,１,2,…,m ,其中m =min {}n M ,,且n ≤N ,M ≤N ,n ,Ｍ,N ∈N ＊ . 三、二项分布一般地,在n 次独立重复试验中,用 X 表示事件A 发生的次数,设每次试验中事件Ａ发生的概率为p ,则P (Ｘ=k )=C 错误!p k (1－ｐ)n － k ,ｋ=０,1,2,…,n 、此时称随机变量Ｘ服从二项分布,记作X ～B (n ,ｐ),并称p 为成功概率.易得二项分布的分布列如下;

第2章随机变量及其分布习题解答

第二章随机变量及其分布 1、解：设公司赔付金额为X ，则X 的可能值为；投保一年内因意外死亡：20万，概率为0.0002 投保一年内因其他原因死亡：5万，概率为0.0010 投保一年内没有死亡：0，概率为1-0.0002-0.0010=0.9988 所以X 2、一袋中有5X 表示取出的三只球中的最大号码，写出随机变量X 的分布律解：X 可以取值3，4，5，分布律为 10 61)4,3,2,1,5()5(1031)3,2,1,4()4(10 11)2,1,3()3(35 2 435 2 335 2 2=?= === ?==== ?= ==C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为也可列为下表 X ： 3， 4，5 P ：10 6, 103,101 3、设在15只同类型零件中有2只是次品，在其中取三次，每次任取一只，作不放回抽样，以X 表示取出次品的只数，（1）求X 的分布律，（2）画出分布律的图形。解：任取三只，其中新含次品个数X 可能为0，1，2个。 35 22 )0(315313= ==C C X P 3512)1(3 15213 12=?==C C C X P 35 1)2(3 15 113 22= ?= =C C C X P 再列为下表 X ： 0， 1， 2 P ： 35 1, 3512,3522 4、进行重复独立实验，设每次成功的概率为p ，失败的概率为q =1－p (0

代数式经典测试题及答案

代数式经典测试题及答案一、选择题 1．若（x +1）（x +n ）＝x 2+mx ﹣2，则m 的值为（） A ．﹣1 B ．1 C ．﹣2 D ．2 【答案】A 【解析】【分析】先将(x+1)(x+n)展开得出一个关于x 的多项式，再将它与x 2+mx-2作比较，即可分别求得m ，n 的值．【详解】解：∵(x+1)(x+n)=x 2+(1+n)x+n ， ∴x 2+(1+n)x+n=x 2+mx-2， ∴12n m n +=??=-? ， ∴m=-1，n=-2．故选A ．【点睛】本题考查了多项式乘多项式的法则以及类比法在解题中的运用． 2．下列各运算中，计算正确的是( ) A ．2a?3a ＝6a B ．(3a 2)3＝27a 6 C ．a 4÷a 2＝2a D ．(a+b)2＝a 2+ab+b 2 【答案】B 【解析】试题解析：A 、2a ?3a =6a 2，故此选项错误； B 、（3a 2）3=27a 6，正确； C 、a 4÷a 2=a 2，故此选项错误； D 、（a+b ）2=a 2+2ab +b 2，故此选项错误；故选B ．【点睛】此题主要考查了积的乘方运算以及同底数幂的除法运算、完全平方公式、单项式乘以单项式等知识，正确化简各式是解题关键． 3．下列运算正确的是（） A ．21ab ab -= B 3=± C ．222()a b a b -=- D ．326()a a = 【答案】D 【解析】【分析】主要考查实数的平方根、幂的乘方、同类项的概念、合并同类项以及完全平方公式.

解： A 项，2ab ab ab -=，故A 项错误； B 3=，故B 项错误； C 项，222()2a b a ab b -=-+，故C 项错误； D 项，幂的乘方，底数不变，指数相乘，32236()a a a ?==. 故选D 【点睛】本题主要考查：（1）实数的平方根只有正数，而算术平方根才有正负. （2）完全平方公式：222()2a b a ab b +=++，222()2a b a ab b -=-+. 4．已知：1+3＝4＝22，1+3+5＝9＝32，1+3+5+7＝16＝42，1+3+5+7+9＝25＝52，…，根据前面各式的规律可猜测：101+103+105+…+199＝（） A ．7500 B ．10000 C ．12500 D ．2500 【答案】A 【解析】【分析】用1至199的奇数的和减去1至99的奇数和即可. 【详解】解：101+103+10 5+107+…+195+197+199 ＝22119919922++????- ? ????? ＝1002﹣502，＝10000﹣2500，＝7500，故选A ．【点睛】本题考查了规律型---数字类规律与探究，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题． 5．下列各式中，计算正确的是（） A ．835a b ab -= B ．352()a a = C ．842a a a ÷= D ．23a a a ?= 【答案】D 【解析】【分析】分别根据合并同类项的法则、同底数幂的乘法法则、幂的乘方法则以及同底数幂除法法则解答即可．

二项分布专题练习

二项分布专题练习 1．已知随机变量X 服从二项分布，X ～B 16,3?? ??? ，则P (X ＝2)＝( )． A ． 316 B ． 4243 C ． 13 243 D ． 80 243 2．设某批电子手表正品率为 34，次品率为1 4 ，现对该批电子手表进行测试，设第X 次首次测到正品，则P (X ＝3)等于( )． A ．223 13C 44??? ??? B ．2 2331C 44 ??? ? ?? C ．2 1344 ??? ??? D ．2 3144 ??? ??? 3．甲、乙两名篮球队员轮流投篮直至某人投中为止，设甲每次投篮命中的概率为0.4，乙投中的概率为0.6，而且不受其他次投篮结果的影响，设投篮的轮数为X ，若甲先投，则P (X ＝k )等于( )． A ．0.6k － 1×0.4 B ．0.24k －1×0.76 C ．0.4k －1×0.6 D ．0.76k － 1×0.24 4．10个球中有一个红球，有放回地抽取，每次取出一球，直到第n 次才取得k (k ≤n )次红球的概率为( )． A ．2191010n k -???? ? ? ???? B ． 191010k n k -???? ? ? ???? C ．1119C 1010k n k k n ---???? ? ????? D ．1 1119C 1010k n k k n ----???? ? ??? ?? 5．在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为 65 81 ，则事件A 在1次试验中发生的概率为( )． A ． 13 B ． 25 C ． 56 D ． 34 6．某一批花生种子，如果每一粒发芽的概率为4 5 ，那么播下4粒种子恰有2粒发芽的概率是__________． 7．一个病人服用某种新药后被治愈的概率为0.9，则服用这种新药的4个病人中至少3人被治愈的概率为__________．(用数字作答) 8．假定人在365天中的任意一天出生的概率是一样的，某班级中有50名同学，其中有两个以上的同学生于元旦的概率是多少？(结果保留四位小数)

(完整版)数据分析(梅长林)第1章习题答案

第1章习题一、习题1.1 解：（1）利用题目中的数据，通过SAS 系统proc univariate 过程计算得到： 139.0=x 7.06387S = 49.898312=S 0.142众数= 51.0g 1-= 08192.5=CV 126129.0g 2-=由得到的数据特征可知道，偏度为负，所以呈做偏态，峰度为负，所以均值两侧的极端值较少。（2） 139.0=M 31.0=R 0.135Q 1= 5.144Q 3= 5.9R 131=-=Q Q 375.1394 1 2141M 31=++= ∧ Q M Q (3) 通过SAS 系统proc capability 得到直方图，并拟合正态分布曲线：

(4) 通过SAS 系统proc univariate 可以画出茎叶图，从茎叶图可以看出数据大致呈对称分布，由于所给数据都是整数，所以叶所代表的小位数都是０。 (5) 通过SAS 系统proc univariate 过程计算得到: 0.971571W 0= 00()H p P W W =≤= 0.1741 取0.05=α，因α>=0.1742p ，故不能拒绝0H ，认为样本来自正态总体分布。通过画ＱＱ图和经验分布曲线和理论分布函数曲线，从图中可以看出ＱＱ图近似的在一条直线上，经验分布曲线的拟合程度也相当好，所以可以进一步说明此样本来自正态总体分布。

二、习题１.２ 7.8574027=x 1.62568785 S = 2.642860982=S 0.13721437g 1= 20.6898884=CV -1.4238025g 2= 由得到的数据特征可知道，偏度为正，所以呈右偏态，峰度为负，所以均值两侧的极端值较少。（2）

《概率论与数理统计》习题随机变量及其分布

第二章随机变量及其分布一. 填空题 1. 设随机变量X ～B(2, p), Y ～B(3, p), 若P(X ≥ 1) =9 5 , 则P(Y ≥ 1) = _________. 解. 9 4951)1(1)0(=-=≥-==X P X P 94)1(2 = -p , 3 1=p 2. 已知随机变量X 只能取－1, 0, 1, 2四个数值, 其相应的概率依次为c c c c 162 , 85,43,21, 则c = ______. 解. 2,16321628543211==+++= c c c c c c 3. 用随机变量X 的分布函数F(x)表示下述概率: P(X ≤ a) = ________. P(X = a) = ________. P(X > a) = ________. P(x 1 < X ≤ x 2) = ________. 解. P(X ≤ a) = F(a) P(X = a) = P(X ≤ a)－P(X < a) = F(a)－F(a －0) P(X > a) = 1－F(a) P(x 1 < X ≤ x 2) = F(x 2)－F(x 1) 4. 设k 在(0, 5)上服从均匀分布, 则02442 =+++k kx x 有实根的概率为_____. 解. k 的分布密度为??? ??=0 51 )(k f 其它50≤≤k P{02442 =+++k kx x 有实根} = P{03216162 ≥--k k } = P{k ≤－1或k ≥ 2} =5 3 515 2=?dk 5. 已知2}{,}{k b k Y P k a k X P =-== =(k = 1, 2, 3), X 与Y 独立, 则a = ____, b = ____, 联合概率分布_____, Z = X + Y 的概率分布为_____. 解. 116,132==++ a a a a . 49 36 ,194= =++b b b b (X, Y)

七年级数学二元一次方程经典练习题及答案

二元一次方程组练习题100道（卷一）（范围：代数：二元一次方程组）一、判断 1、??? ??-==312y x 是方程组?????? ?=-=-9 1032 6 5 23y x y x 的解 …………（） 2、方程组? ? ?=+-=5231y x x y 的解是方程3x -2y =13的一个解（） 3、由两个二元一次方程组成方程组一定是二元一次方程组（） 4、方程组???????=-++=+++2 5323 473 5 23y x y x ，可以转化为???-=--=+27651223y x y x （） 5、若(a 2-1)x 2 +(a -1)x +(2a -3)y =0是二元一次方程，则a 的值为±1（） 6、若x +y =0，且|x |=2，则y 的值为2 …………（） 7、方程组? ? ?=+-=+81043y x x m my mx 有唯一的解，那么m 的值为m ≠-5 …………（） 8、方程组?? ???=+=+62 3 131 y x y x 有无数多个解 …………（） 9、x +y =5且x ，y 的绝对值都小于5的整数解共有5组 …………（） 10、方程组? ? ?=+=-351 3y x y x 的解是方程x +5y =3的解，反过来方程x +5y =3的解也是方程组 ?? ?=+=-3 51 3y x y x 的解 ………（） 11、若|a +5|=5，a +b =1则3 2 -的值为b a ………（） 12、在方程4x -3y =7里，如果用x 的代数式表示y ，则4 37y x += （）二、选择： 13、任何一个二元一次方程都有（）（A ）一个解；（B ）两个解；（C ）三个解；（D ）无数多个解； 14、一个两位数，它的个位数字与十位数字之和为6，那么符合条件的两位数的个数有（）

二项分布经典例题+测验题资料

二项分布经典例题+测验题

二项分布 1．n 次独立重复实验一般地，由n 次实验构成，且每次实验相互独立完成，每次实验的结果仅有两种对立的状态，即A 与A ，每次实验中()0P A p =>。我们将这样的实验称为n 次独立重复实验，也称为伯努利实验。（1）独立重复实验满足的条件第一：每次实验是在同样条件下进行的；第二：各次实验中的事件是互相独立的；第三：每次实验都只有两种结果。（2）n 次独立重复实验中事件A 恰好发生k 次的概率 ()P X k ==(1)k k n k n C p p --。 2．二项分布若随机变量X 的分布列为()P X k ==k k n k n C p q -，其中 0 1.1,0,1,2,,,p p q k n <<+==则称X 服从参数为,n p 的二项分布，记作(,)X B n p 。 1．一盒零件中有9个正品和3个次品，每次取一个零件，如果取出的次品不再放回，求在取得正品前已取出的次品数X 的概率分布。 3.甲乙两人各进行3次射击，甲每次击中目标的概率为2 1，乙每次击中目标的概率为3 2. （1）记甲击中目标的此时为ξ，求ξ的分布列及数学期望；（2）求乙至多击中目标2次的概率；（3）求甲恰好比乙多击中目标2次的概率. 【巩固练习】

1.（2012年高考（浙江理））已知箱中装有4个白球和5个黑球, 且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和. (Ⅰ)求X的分布列。 (Ⅱ)求X的数学期望E(X). 2．（2012年高考（重庆理））(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.) 甲、乙两人轮流投篮,每人每次投一球,.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为1 3,乙每次投篮投中的概率为1 2 ,且各次投篮互不影响. (Ⅰ) 求甲获胜的概率。 (Ⅱ) 求投篮结束时甲的投篮次数的分布列与期望 3．设篮球队A与B进行比赛，每场比赛均有一队胜，若有一队胜4场则比赛宣告结束，假定,A B在每场比赛中获胜的概率都是 1 2 ，试求需要比赛场数的期望． 3．（2012年高考（辽宁理））电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图。

二维随机变量及其分布题目

一、单项选择题 1．设随机变量21,X X 独立，且2 1 }1{}0{= ===i i X P X P （2,1=i ），那么下列结论正确的是（） A .21X X = B .1}{21==X X P C .2 1 }{21= =X X P D .以上都不正确 2设X 与Y 相互独立，X 服从参数为12的0—1分布，Y 服从参数为1 3 的0—1分布，则方程 220t Xt Y ++=中t 有相同实根的概率为（A ） 13 （B ）12 （C ）16 （D ）2 3 [] 3．设二维随机变量（X ，Y ）的概率密度为 ()22 ,02,14, (,)0, .k x y x y f x y ?+<<<

北师大版七年级数学上册《代数式》典型例题(含答案)

《代数式》典型例题例1 列代数式，并求值．有两种学生用本，一种单价是0.25元，另一种单价是0.28元，买这两种本的数分别是m 和n ．（1）问共需要多少元？（2）如果单价是0.25元的本和单价是0.28元的本分别买了20和25本，问共花了多少钱？例2 某城市居民用电每千瓦时（度）0.33元，某户本月底电能表显示数m ，上月底电能表显示数为n ，（1）用m 和n 把本月电费表示出来；（2）若本月底电能表显示数是1601，上月底电能表显示数为1497，问本月的电费是多少？例3 春节前夕，铁路为了控制客流，使其卧铺票票价上浮20％，春节期间按原价下浮10％，若某地到北京的卧铺票原价是x 元，如果在春节期间乘坐要比春节前少花多少钱，用x 表示出；当228=x 时，求这个代数式的值。例4 22b a -可以解释为___________．例5 一个三位数，百位数上的数是a ，十位上的数是b ，个位上的数是c ．（1）用代数式表示这个三位数．（2）把它的三位数字颠倒过来，所得的三位数又该怎样表示？例6 选择题 1．x 的3倍与y 的2倍的和，除以x 的2倍与y 的3倍的差，写成的代数式是（） A ． y x y x 3223-+ B ．x y y x 2323-+ C ．y x y x 3223-+ D ．y x y x 2223-+ 2．如图，正方形的边长是a ，圆弧的半径也是a ，图中阴影部分的面积是（）

A ．224a a -π B ．22a a π- C ．22a a -π D ．224a a π- 例7 通过设2003 1413121,20021413121++++=++++= b a 来计算： ).20021413121()200314131211()20031413121()200214131211(++++?+++++-++++?+++++ 例8 按给的例子，把输出的数据填上例9 对于正数，运算“*”定义为b a a b b a +=*，求)333**（．

二项分布经典例题+测验题

二项分布 1．n 次独立重复实验一般地，由n 次实验构成，且每次实验相互独立完成，每次实验的结果仅有两种对立的状态，即A 与A ，每次实验中()0P A p =>。我们将这样的实验称为n 次独立重复实验，也称为伯努利实验。（1）独立重复实验满足的条件第一：每次实验是在同样条件下进行的；第二：各次实验中的事件是互相独立的；第三：每次实验都只有两种结果。（2）n 次独立重复实验中事件A 恰好发生k 次的概率 ()P X k ==(1)k k n k n C p p --。 2．二项分布若随机变量X 的分布列为()P X k == k k n k n C p q -，其中 0 1.1,0,1,2,,,p p q k n <<+==则称X 服从参数为,n p 的二项分布，记作(,)X B n p 。 1．一盒零件中有9个正品和3个次品，每次取一个零件，如果取出的次品不再放回，求在取得正品前已取出的次品数X 的概率分布。 3.甲乙两人各进行3次射击，甲每次击中目标的概率为2 1，乙每次击中目标的概率为3 2 . （1）记甲击中目标的此时为ξ，求ξ的分布列及数学期望；（2）求乙至多击中目标2次的概率；（3）求甲恰好比乙多击中目标2次的概率. 【巩固练习】 1.（2012年高考（浙江理））已知箱中装有4个白球和5个黑球,且

规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和. (Ⅰ)求X的分布列。 (Ⅱ)求X的数学期望E(X). 2．（2012年高考（重庆理））(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.) 甲、乙两人轮流投篮,每人每次投一球,.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为1 3,乙每次投篮投中的概率为1 2 ,且各次投篮互不影响. (Ⅰ) 求甲获胜的概率。 (Ⅱ) 求投篮结束时甲的投篮次数的分布列与期望 3．设篮球队A与B进行比赛，每场比赛均有一队胜，若有一队胜 4场则比赛宣告结束，假定,A B在每场比赛中获胜的概率都是1 2 ，试求需要比赛场数的期望． 3．（2012年高考（辽宁理））电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查. 下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图。

第二章__随机变量及其概率分布_考试模拟题答案

第二章随机变量及其概率分布考试模拟题 (共90分) 一．选择题(每题2分共20分) 1．F(X)是随机变量X 的分布函数，则下列结论不正确的是（ B ） A.≤0F(x )1≤ B.F(x )=P{X=x } C.F(x )=P{X x ≤} D.F(∞+)=1, F(∞-)=0 解析： A,C,D 都是对于分布函数的正确结论，请记住正确结论！B 是错误的。 2．设随机变量X 的分布函数律为如下表格：F(x)为其分布函数，则F(5)=( C ) A.0.3 B.0.5 C.0.6 D.0.4 解析：由分布函数定义F(5)=P{X ≤5}=P{X=0}+P{X=2}+P{X=4}=0.1+0.2+0.3=0.6 3．下列函数可以作为随机变量分布函数的是（ D ） 4x 01≤≤x 2x 10<≤x A.F(x)= B.F(x)= 1 其它 2 其它 -1 x<0 0 x<0 C.F(x)= 2x 10<≤x D.F(x)= 2x 5.00<≤x 1 其它 1 x ≥0.5 解析：由分布函数F(x)性质：01)(≤≤x F ，A,B,C 都不满足这个性质，选D 4 x 31<<-x 4．设X 的密度函数为f(x)= 则P{-2

A. 0 B.83 C. 43 D. 85 解析：P{-2

代数式知识点、经典例题、习题及答案(供参考)

1.2 代数式【考纲说明】 1、理解字母表示数的意义及用代数式表示规律。 2、用代数式表示实际问题中的数量关系，求代数式的值。【知识梳理】 1、代数式：指含有字母的数学表达式。 2、一个代数式由数、表示数的字母、运算符号组成。单个字母或数字也是代数式。 3、代数式的值：一般地，用数值代替代数式里的字母，计算后所得的结果叫做代数式的值。 4、用字母表示数的规范格式：（1）、数和表示数的字母相乘，或字母和字母相乘时，乘号可以省略不写，或用“.”来代替。（2）、当数和字母相乘，省略乘号时，要把数字写到前面，字母写后面。如：100a或100?a，na或n?a。（3）、后面接单位的相加式子要用括号括起来。如：（5s ）时（4）、除法运算写成分数形式。（5）、带分数与字母相乘时，带分数要写成假分数的形式。 5、列代数式时要注意：（1）语言叙述中关键词的意义，如“大”“小”“增加”“减少”。 “倍”“几分之几”等词语与代数式中的运算符号之间的关系。（2）要理清运算顺序和正确使用括号，以防出现颠倒等错误，例如“积的和”与“和的积”“平方差”“差的平方”等等。（3）在同一问题中，不同的数量必须用不同的字母表示。【经典例题】【例1】（2012重庆，9，4分）下列图形都是由同样大小的五角星按一定的规律组成。其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五

角星，…，则第⑥个图形中的五角星的个数为（）【解析】仔细观察图形的特点，它们都是轴对称图形，每一行的个数都是偶数，分别是2，4，6，…，6,4,2，故第⑥个图形中五角星的个数为2+4+6+8+10+12+10+8+6+4+2=72。答案：D 【例2】（2011甘肃兰州，20，4分）如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去，已知第一个矩形的面积为1，则第n 个矩形的面积为 . 【解析】由中点四边形的性质可知，每次所得新中点四边形的面积是前一个图形的 12，故后一个矩形的面积是前一个矩形的14 ，所以第n 个矩形的面积是第一个矩形面积的1221142n n --????= ? ?????，已知第一个矩形面积为1，则第n 个矩形的面积为2212n -?? ???。【例3】按一定规律排列的一列数依次为 111111,,,,,,2310152635 …，按此规律，第7个数是。【解析】先观察分子：都是1；再观察分母：2,3,10,15,26，…与一些平方数1,4,9,16，…都差1,2=12+1，3=22-1，10=32+1，15=42-1，26=52+1，…，这样第7个数为 2117150=+。答案：150 【例4】已知： 114a b -=，则2227a ab b a b ab ---+的值为（） A ．6 B ．--6 C ．215- D ．27 - 【解析】由已知114a b -=，得4b a ab -=， ∴4,4, 2()242 6.2272()787b a ab a b ab a ab b a b ab ab ab a b ab a b ab ab ab ∴-=-=-------∴===-+-+-+答案：A 【课堂练习】 1、（2012湖北武汉，9，3分）一列数a1，a2，a3，…，其中a1= 111,21n n a a -=+（n 为不

正态分布及其经典习题和答案

专题：正态分布【知识网络】 1、取有限值的离散型随机变量均值、方差的概念； 2、能计算简单离散型随机变量的均值、方差，并能解决一些实际问题； 3、通过实际问题，借助直观（如实际问题的直观图），认识正态分布、曲线的特点及曲线所表示的意义。【典型例题】例1：（1）已知随机变量X 服从二项分布，且E （X ）=2.4，V （X ）=1.44，则二项分布的参数n ，p 的值为（） A ．n=4，p=0.6 B ．n=6,p=0.4 C ．n=8，p=0.3 D ．n=24，p=0.1 答案：B 。解析：()4.2==np X E ，()44.1)1(=-=p np X V 。（2）正态曲线下、横轴上，从均数到∞+的面积为( )。 A ．95% B ．50% C ．97.5% D ．不能确定（与标准差的大小有关）答案：B 。解析：由正态曲线的特点知。（3）某班有48名同学，一次考试后的数学成绩服从正态分布，平均分为80，标准差为10，理论上说在80分到90分的人数是（） A 32 B 16 C 8 D 20 答案：B 。解析:数学成绩是X —N(80,102)， 8080 9080(8090)(01)0.3413,480.34131610 10P X P Z P Z --??≤≤=≤≤=≤≤≈?≈ ???。（4）从1，2，3，4，5这五个数中任取两个数，这两个数之积的数学期望为___________ 。答案：8.5。解析：设两数之积为X ， ∴E(X)=8.5. （5）如图，两个正态分布曲线图： 1为)(1 ,1x σμ?，2为)(22x σμ?，则1μ 2μ，1σ 2σ答案：＜，＞。解析：由正态密度曲线图象的特征知。例2：甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格. （Ⅰ）求甲答对试题数ξ的概率分布及数学期望；（Ⅱ）求甲、乙两人至少有一人考试合格的概率. 答案：解：（Ⅰ）依题意，甲答对试题数ξ的概率分布如下：甲答对试题数ξ的数学期望 E ξ=5 9 61321210313010=?+?+?+? . （Ⅱ）设甲、乙两人考试合格的事件分别为A 、B ，则

代数式求值经典题型(含详细答案)

代数式求值经典题型【编著】黄勇权经典题型： 1、x+x 1 =3，求代数式 x 2 -2 x 1的值。 2、已知a+b=3ab ，求代数式b 1 a 1+的值。 3、已知 x 2 -5x+1=0,求代数式x 1x +的值。 4、已知x-y=3，求代数式（x+1） 2 -2x+y （y-2x ）的值。 5、已知x-y=2，xy=3，求代数式x 2 -xy 6+y 2的值。 6、已知y x =2，则x y -x 的值是多少？

7、若2y 1x 1=+，求代数式：3y xy -3x y 3xy -x ++的值。 8、已知5-x =4y-4-y 2，则代数式2x-3+4y 的值是多少？ 9、化简求值，12x x 1-x 2 ++÷）（1x 2 1+-，其中x=13- 10、x 2-4x+1=0，求代数式：x 2 +2 x 1 的值。【答案】 1、x+x 1 =3，求代数式：x 2 -2 x 1的值。解：x 2 -2 x 1 =（x+x 1）（x-x 1 ） =（x+x 1 ）2x 1-x ）（ =（x+x 1 ）2 2x 12x +- =（x+x 1）4x 12x 2 2 -++ =（x+x 1）4x 1x 2 -+）（将 x+x 1 =3 代入式中

=3×432- =35 2、已知a+b=3ab ，求代数式：b 1 a 1+的值。解：b 1 a 1+ =ab b a + 将a+b=3ab 代入式中 =3 3、已知x 2 -5x+1=0,求代数式：x 1 x +的值。解：因x 2 -5x+1=0，等式两边同时除以x 则有：x 0 x 1x x 5x x 2=+- 化简得：x-5+x 1 =0 把-5移到等号的右边，得： x 1 x +=5

二项分布经典例题练习题

二项分布 1．n 次独立重复试验一般地，由n 次试验构成，且每次试验相互独立完成，每次试验的结果仅有两种对立的状态，即A 与A ，每次试验中()0P A p =>。我们将这样的试验称为n 次独立重复试验，也称为伯努利试验。（1）独立重复试验满足的条件第一：每次试验是在同样条件下进行的；第二：各次试验中的事件是互相独立的；第三：每次试验都只有两种结果。（2）n 次独立重复试验中事件A 恰好发生k 次的概率()P X k ==(1)k k n k n C p p --。 2．二项分布若随机变量X 的分布列为()P X k ==k k n k n C p q -，其中0 1.1,0,1,2,,,p p q k n <<+==L 则称X 服从参数为,n p 的二项分布，记作(,)X B n p :。 1．一盒零件中有9个正品和3个次品，每次取一个零件，如果取出的次品不再放回，求在取得正品前已取出的次品数X 的概率分布。 2.一名学生每天骑车上学，从他家到学校的途中有6个交通岗，假设他在各个交通岗遇到红灯的事件是相互独立的，并且概率都是31 . (1)设ξ为这名学生在途中遇到红灯的次数，求ξ的分布列； (2)设η为这名学生在首次停车前经过的路口数，求η的分布列；

(3)求这名学生在途中至少遇到一次红灯的概率. 3.甲乙两人各进行3次射击，甲每次击中目标的概率为 21，乙每次击中目标的概率为3 2. （1）记甲击中目标的此时为ξ，求ξ的分布列及数学期望；（2）求乙至多击中目标2次的概率；（3）求甲恰好比乙多击中目标2次的概率. 【巩固练习】 1.（2012年高考（浙江理））已知箱中装有4个白球和5个黑球,且规定:取出一个白球的 2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X 为取出3球所得分数之和. (Ⅰ)求X 的分布列; (Ⅱ)求X 的数学期望E (X ). 2．（2012年高考（重庆理））(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.) 甲、乙两人轮流投篮,每人每次投一球,.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为1 3 ,乙每次投篮投中的概率为1 2 ,且各次投篮互不影响. (Ⅰ)求甲获胜的概率; (Ⅱ)求投篮结束时甲的投篮次数ξ的分布列与期望

第二章随机变量与分布函数习题

第二章：随机变量与分布函数习题一、“离散型随机变量与分布函数”习题： 1. 射手对靶子进行射击，用X 表示击中的环数，已知击中一环的概率为0.2，击中两环的概率为0.8；求：（1）X 的分布列及分布函数；（2）()()10,1≤<≥X P X P . 2. 射手对靶子进行射击，一次射击的命中率为0.8，现在连续射击三枪，用X 表示三枪中命中的次数，求：（1）X 的分布列及分布函数；（2）A “至少命中两枪”的概率. 3. 设随机变量X 的分布函数为 ()()???? ???≥<≤<≤--<=≤=31 318.0114.010 x x x x x X P x F 求：X 的分布列. 4. 设随机变量X 的分布函数为 ()??? ? ????? >≤≤<=2120sin 00ππx x x A x x F 求：（1）A =？（2）??? ??<6πx P . 5. 设随机变量X 的分布列为??? ? ??--22121101q q ；求：（1）q=？（2）X 的分布函数. 6. 某设备由三个独立工作的元件构成，该设备在一次试验中每个元件发生故障的概率为 0.1，求该设备在一次试验在中发生故障的元件数的分布列. 7. 将一颗骰子投掷两次，以X 表示两次所得点数之和、Y 表示两次中所得的小的点数；分别求X 与Y 的分布列. 8. 设随机变量X ~()p B ,2，随机变量Y ~()p B ,3；已知()9 5 1=≥X P ，求：()1≥Y P . 二、“连续型随机变量与分布函数”习题： 1. 设()()??? ??<>≥=-00 0,0212 x a x e a x x f a x ； ()?????<<=其他0 0cos 21 2 πx x x f ； ()????? <<-=其他0 22cos 3ππx x x f ；（1）以上()()()x f x f x f 321,,是否是某随机变量X 的分布密度函数？

正态分布附其经典习题及答案

25.3正态分布【知识网络】 1、取有限值的离散型随机变量均值、方差的概念； 2、能计算简单离散型随机变量的均值、方差，并能解决一些实际问题； 3、通过实际问题，借助直观（如实际问题的直观图），认识正态分布、曲线的特点及曲线所表示的意义。【典型例题】例1：（1）已知随机变量X 服从二项分布，且E （X ）=2.4，V （X ）=1.44，则二项分布的参数n ，p 的值为（） A ．n=4，p=0.6 B ．n=6,p=0.4 C ．n=8，p=0.3 D ．n=24，p=0.1 答案：B 。解析：()4.2==np X E ，()44.1)1(=-=p np X V 。（2）正态曲线下、横轴上，从均数到∞+的面积为( )。 A ．95% B ．50% C ．97.5% D ．不能确定（与标准差的大小有关）答案：B 。解析：由正态曲线的特点知。（3）某班有48名同学，一次考试后的数学成绩服从正态分布，平均分为80，标准差为10，理论上说在80分到90分的人数是（） A 32 B 16 C 8 D 20 答案：B 。解析:数学成绩是X —N(80,102 )， 8080 9080(8090)(01)0.3413,480.3413161010P X P Z P Z --??≤≤=≤≤=≤≤≈?≈ ???。（4）从1，2，3，4，5这五个数中任取两个数，这两个数之积的数学期望为___________。 ∴ （5）如图，两个正态分布曲线图： 1为)(1 ,1x σμ?，2为)(22x σμ?，则1μ2μ，1σ2σ（填大于，小于）答案：＜，＞。解析：由正态密度曲线图象的特征知。例2 ：甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格. （Ⅰ）求甲答对试题数ξ的概率分布及数学期望；（Ⅱ）求甲、乙两人至少有一人考试合格的概率. 答案：解：（Ⅰ）依题意，甲答对试题数ξ的概率分布如下：甲答对试题数ξ的数学期望 E ξ=5 9 61321210313010=?+?+?+? . （Ⅱ）设甲、乙两人考试合格的事件分别为A 、B ，则

相关文档

最新文档