初中常用数学模型完整版.doc
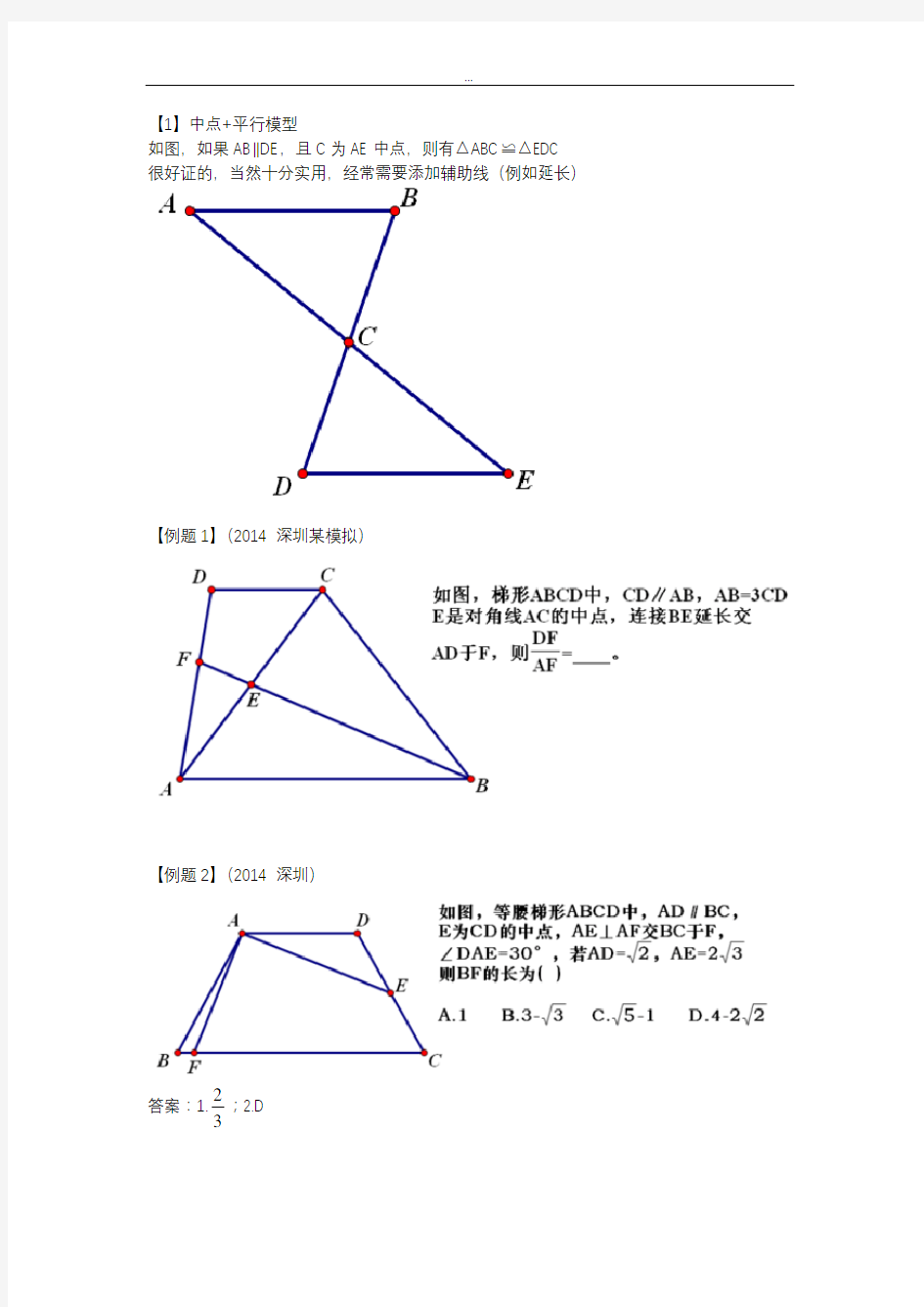
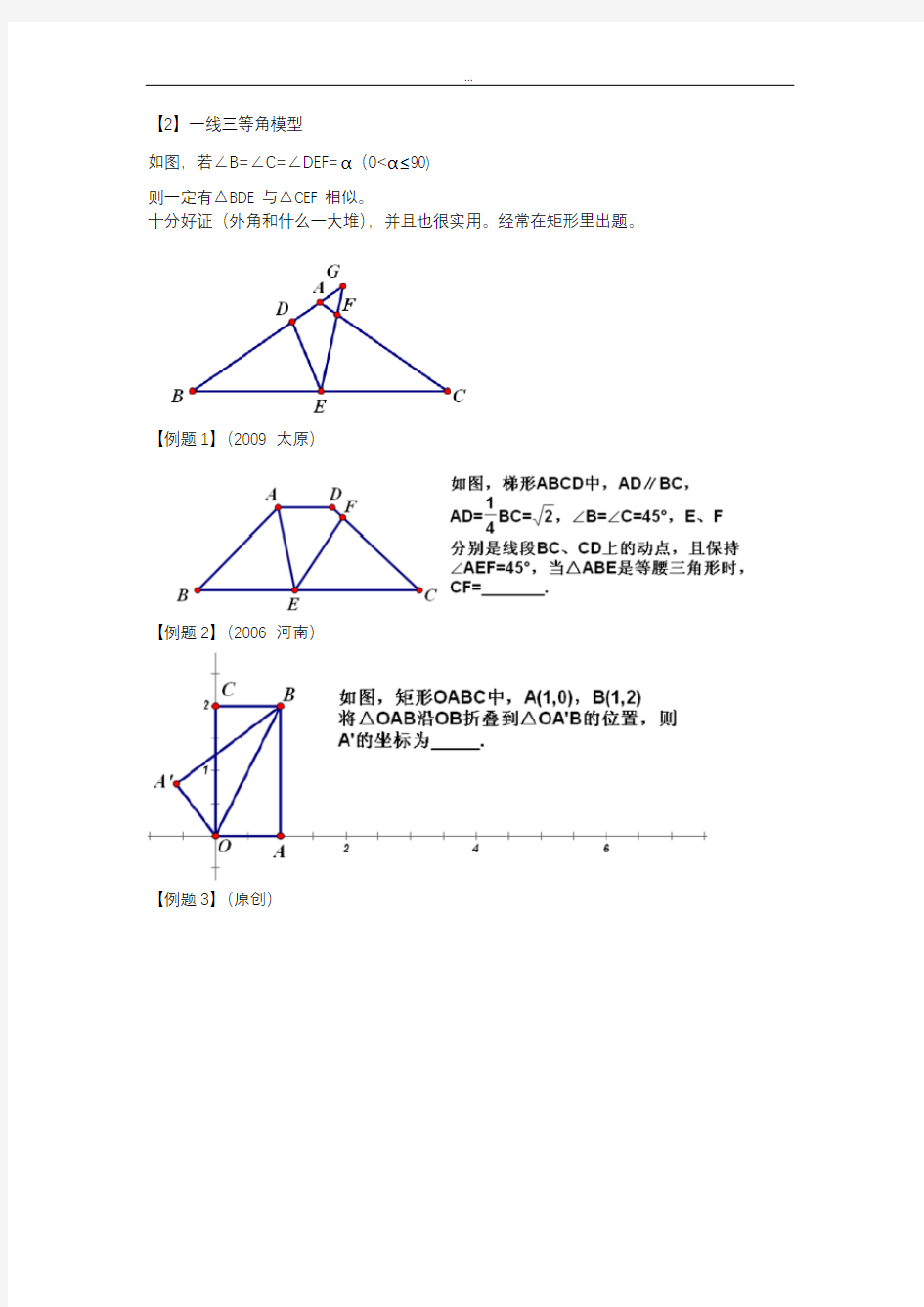
如图,如果AB ‖DE ,且C 为AE 中点,则有△ABC ≌△EDC 很好证的,当然十分实用,经常需要添加辅助线(例如延长)
【例题1】(2014 深圳某模拟)
【例题2】(2014 深圳)
答案:1.3
2
;2.D
如图,若∠B=∠C=∠DEF=α(0<α≤90)
则一定有△BDE与△CEF相似。
十分好证(外角和什么一大堆),并且也很实用。经常在矩形里出题。
【例题1】(2009 太原)
【例题2】(2006 河南)
【例题3】(原创)
答案:1. 2或3-24或
2
5
2.(5453-,)
【3】巧造旋转模型
在某些几何题中,往往有一些奇怪的结论,此时可以通过几何三大变换之一【旋转】求解。 巧造旋转往往要有一定的等量关系和特殊角度,如下题:
通过观察可得∠ABC=∠C=45°,AB=AC 。
我们可以将△ACD 绕A 顺时针旋转90°得到△ABE ,使得AC 与AB 重合。 那么就有EB ⊥BC ,而在RT △AED 中,DE 2=2AD 2(等腰直角三角形) 所以BE 2+BD 2=DE 2,即BD 2+CD 2=2AD 2
是不是赶脚很难想到?要学会判断,这种感觉是要练出来的! 【例题1】(2014 武汉)
【例题2】
【例题3】(2014 菏泽改编)
答案:1.41 2.9 3.(1.)2,(2.)直角三角形,旋转后证全等,证明略【4】等腰模型
这是一个很基础的模型——什么样的结构会生成等腰三角形
首先:平行+角平分线,
如图,若AD‖BE,BC平分∠ABE,则AB=AC,很好证的,导角即可。
其次:垂直+角平分
这个不难理解,因为等腰三角形三线合一。
这种模型很常用,常常需要做辅助线(延长之类)
【例题1】(原创)
AB‖CD
【例题2】(原创)
【例题3】(改编)
1.11
2.3
3.延长CD交AB于M,利用中位线,证明略【5】倍长中线法
常考,选填大证明都可能会用。
是的!又是中点,中点用的很多啊= =
这个模型怎么用?先要判断。做题的时候看见中点,先找有没有可以直接用的,没有就找就没有平行+中点,再没有就要想了没事摆个中点在这里有啥用?这时试试倍长中线。记住一句话:“倍长中线,定得全等”
先来举一个例子,吧里很经典的一题。←_←
解:延长AD,使DE=AD,连接CE(做这种题不变的辅助线说明)
∵AD=DE,BD=CD,∠ADB=∠CDE
∴△ADB≌△EDC
∴CE=AB=3
∴4-3 故1/2 这样就迎刃而解了,还有好多好多题,需要用到这个 【例题1】(改编) 【例题2】(改编) 2 1.6 2.证明略,( 3.)2 【6】几何最值模型.1 最值是中考最常考的题目,选择、填空、大题都可能有。 几何最值——当然数学书上是找不到的,所以这要我们平时多了解这种题的做题技巧 一般有三种:线段最值、折线最值、周长面积最值 最值不好学,先从简单学起。 1.首先最简单的:点到直线的距离垂线段最短、化曲为直,这是最基础的。 2.其次:通过对称寻找最值,经典的【建设奶站】模型。 3.折叠最值:三角形三边关系解题,寻找【三点共线】最关键。 举个例子: 第一问做一个垂线就行了。 第二问是重点,作C关于l的对称点C',连接C'B,则C'B与l的交点为Q,此时BQ+CQ 最小值为BC'。用三角形三边关系证明,尝试一下吧 第三问同样重点(虽然没第二问那么常考),M可不是AD与l的交点,这时因为A、D在异 侧讨论差值不方便,故作对称。则AD'延长线与l 的交点为M ,此时lAM-DMl 的最小值为D'M 。这同样用三角形三边关系证。 考试的时候辅助线要写,道理不用。 简单归纳,同侧最小找轴对称、异侧最大对称加延长,注意图形对称性 好了先到这里,下面是例题 【例题1】(改编) 【例题2】(原创) 1.4 2.(1.)2-6;(2.)①62;②F ABG 、?=∠15为BG 的垂直平分线与BC 的交点 【7】几何最值模型.2 初中大部分的几何最值都要化曲为直,一般我们称为【三点共线】,下面是折叠的一题。 做这种题,最重要找的是不变量。如图,CD 是不变量6,AD 也是不变量√61,只有E 、F 在动 现在开始分析,先把AD连接,得到一个不变的线段。而在△ADF中,由三边公式可知 AF>AD-DF,这有什么用?这个意思是万一A、F、D三点共线了,不就是AF=AD-DF了?就是说当形成了三角形的时候,AF都是大于AD-DF的,三点共线时,AF=AD-DF,这样AF 不就最短了吗?所以AFmin=√61 -6 还有一种经典的题: 照样先找不变量,发现AB、BC不变为4,其余没有。这种题的不变量一般隐藏在某些条件中 分析一下:等边你还没用,∠AOB=90°的条件也没用,综合考虑,取AB中点,因为直角三角形斜边中线等于斜边一半,所以OD=2,由等边三角形,可知CD=2√3,现在用三点共线,很快得到OC=OD+CD时OC最大,所以OC最大值为2+2√3 这种题要多练,寻找感觉。主要是找不变量,这在动点问题中十分重要。 【例题1】 【例题2】(呵呵你会发现我偷懒了) 【例题3】 14 答案:1.5 2.1 3. 2 【8】十分重要! 反比例函数中的模型 俗话说的好,选填里面出得最难的不是几何题,而是反比例综合,要想稳拿3分,先掌握这些 首先简单搞起 ①这个很简单,已知某点坐标(m,n)求过该点的反比例函数表达式y=k/x,则k=mn(k≠0) ②已知反比例函数图象分别交矩形AOBC的边AC、BC于D、E,连接OC,则: S△OCD=S△OEC ③在上图的基础上,有AD:CD=BE:CE, 当然如果连接DE、AB,DE和AB一定是平行的。 ④这个不大常用,但是也挺重要,如图,任意直线AB与双曲线交于G、H,则AG=BH 那么看到AG=GH的话就立马反应过来三段都等了。 ⑤这个十分常用,在上图的基础上,S△OGH=S梯形GEFH ⑥看着不爽系列(雾)补全图形,常常有些梯形是要补全成矩形的,如此挖掘隐含条件就差不多是这些,记住做反比例函数题的核心点:面积转换最重要,各种垂直显神通意思就是没思路的时候做些垂直的辅助线,会有相似等。 【例题1】 【例题2】 【例题3】 【例题4】 答案:1.3 7 2.x y 43 3.4 4.
