行走机器人避障问题数学建模

机器人行走问题

摘要

本文研究了机器人避障最短路径的问题。主要研究了在一个区域中存在四个障碍物，由出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的两种情形。我们通过证明具有圆形限定区域的最短路径是由两部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界，这两部分是相切的，互相连接的。依据这个结果，我们可以认为最短路径一定是由线和圆弧做组成，因此我们建立了线圆结构，这样无论路径多么复杂，我们都可以将路径划分为若干个这种线圆结构来求解。对于途中经过节点的再到达目标点的状况，我们采用了两种方案，一种是在拐点和节点都采用最小转弯半径的形式，另一种是适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点。然后建立了最优化模型对两种方案分别进行求解。

问题一，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径：

R→A 最短路径为：70.5076

R→B 最短路径为：107.9587

R→C 最短路径为：102.0514

问题二，我们方案都进行优化，求得最终结果：

第一种方案最短路径为：156.471

第二种方案最短路径为：157.752

关键词最短路径最优化模型避障路径解析几何

一、问题重述

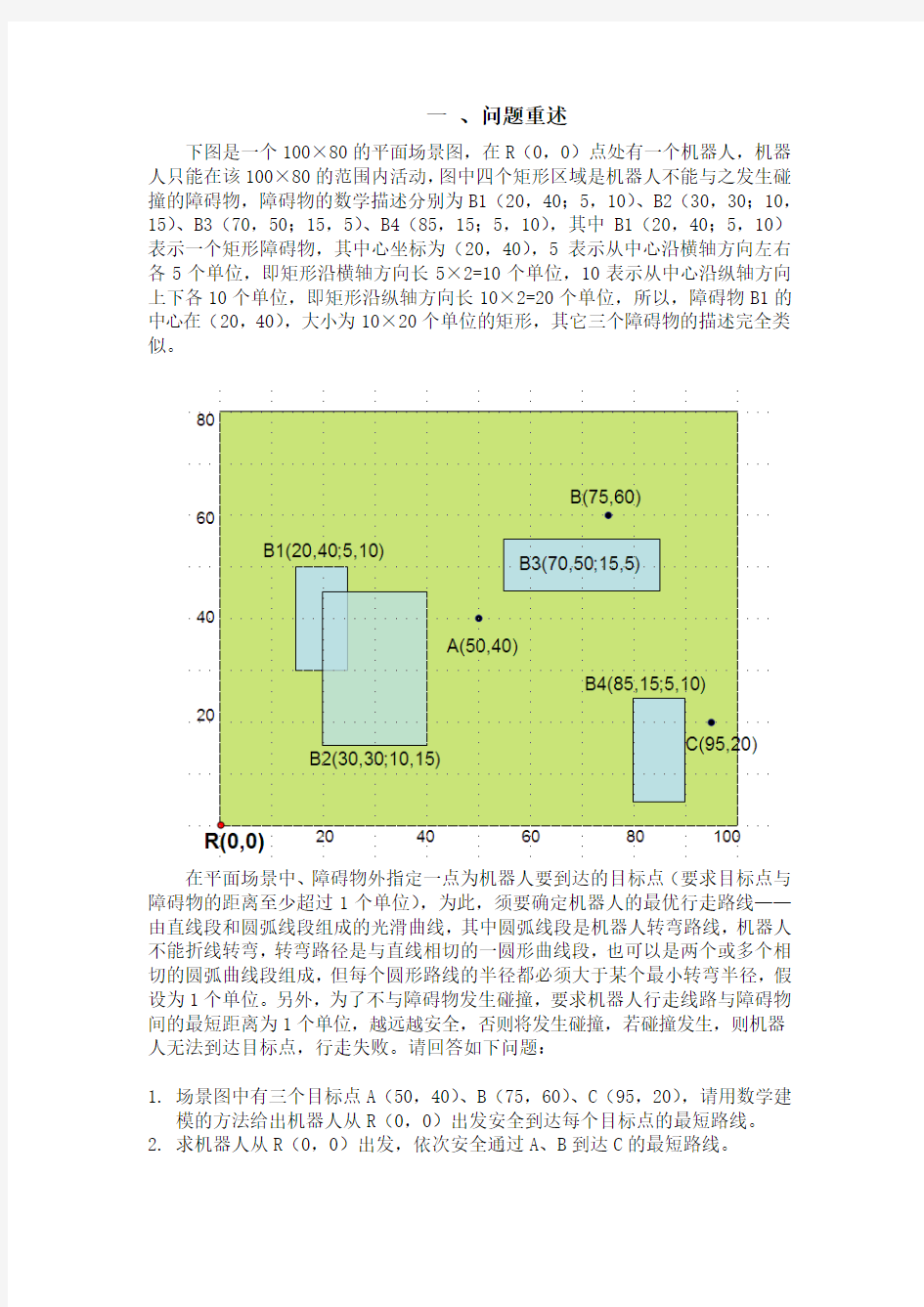
下图是一个100×80的平面场景图，在R（0，0）点处有一个机器人，机器人只能在该100×80的范围内活动，图中四个矩形区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述分别为B1（20，40；5，10）、B2（30，30；10，15）、B3（70，50；15，5）、B4（85，15；5，10），其中B1（20，40；5，10）表示一个矩形障碍物，其中心坐标为（20，40），5表示从中心沿横轴方向左右各5个单位，即矩形沿横轴方向长5×2=10个单位，10表示从中心沿纵轴方向上下各10个单位，即矩形沿纵轴方向长10×2=20个单位，所以，障碍物B1的中心在（20，40），大小为10×20个单位的矩形，其它三个障碍物的描述完全类似。

在平面场景中、障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过1个单位），为此，须要确定机器人的最优行走路线——由直线段和圆弧线段组成的光滑曲线，其中圆弧线段是机器人转弯路线，机器人不能折线转弯，转弯路径是与直线相切的一圆形曲线段，也可以是两个或多个相切的圆弧曲线段组成，但每个圆形路线的半径都必须大于某个最小转弯半径，假设为1个单位。另外，为了不与障碍物发生碰撞，要求机器人行走线路与障碍物间的最短距离为1个单位，越远越安全，否则将发生碰撞，若碰撞发生，则机器人无法到达目标点，行走失败。请回答如下问题：

1.场景图中有三个目标点A（50，40）、B（75，60）、C（95，20），请用数学建

模的方法给出机器人从R（0，0）出发安全到达每个目标点的最短路线。

2.求机器人从R（0，0）出发，依次安全通过A、B到达C的最短路线。

二、问题分析

1、问题一中要求求定点R（0, 0）按照一定的行走规则绕过障碍物到达目标点

的最短路径，我们先可以包络线画出机器人行走的危险区域，这样的话，拐角处就是一个半径为1的四分之一圆弧，通过那么然后采用拉绳子的方法寻找可能的最短路径（比如求R和A之间的最短路径，我们就可以连接R和A 之间的一段绳子，以拐角处的圆弧为支撑拉紧，那么这段绳子的长度便是R 到A的一条可能的最短路径），然后采用穷举法列出R到每个目标点的可能路径的最短路径，然后比较其大小便可得出R到目标点的最短路径。

2、问题二中要求求定点R（0， 0）经过中间的若干点按照一定的规则绕过障碍

物到达目标点，这使我们考虑就不仅仅是经过障碍物拐点的问题，也应该考虑经过路径中的目标点处转弯的问题，这时简单的线圆结构就不能解决这种问题，我们在拐点及途中目标点处都采用最小转弯半径的形式，也可以适当的变换拐点处的拐弯半径，使机器人能够沿直线通过途中的目标点，然后建立优化模型对这两种方案分别进行优化，最终求得最短路径。

三、模型假设

1、假设障碍物全是矩形。

2、假设机器人能够抽象成点来处理。

四、符号说明

五、模型的建立

5.1先来证明一个猜想：

猜想一：具有圆形限定区域的最短路径是由两部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界，这两部分是相切的，互相连接的。（即问题分析中的拉绳子拉到最紧时的状况）

证明：假设在平面中有A （a ，0）和B （-a ，0）两点，中间有一个半圆形的障碍物，证明从A 到B 的最路径为A

B 。

平面上连接两点最短的路径是通过这两点的直线段，但是连接两点的线段于障碍物相交，所以设法尝试折线路径。在y 轴上取一点C （0，y ），若y 适当大，则折线ACB 与障碍物不相交，折线ACB 的长度为：

||ACB =显然||ACB 随着y 的减小而减小，减小y 得y →1y ，即1C C →,使得1AC 与1C B 与障碍物相切，切点分别为E 和F,显然1AC B 是这种折线路径中最短的。由于满足0<<

2π的角满足<,所以易知弧度EF 小于1EC F 的长， 即

AE ++FB<1AC B ,记线段AE 、弧度EF 、线段FB 为AEFB,那么AEFB 比任何折线路径都短。

下面在考察一条不穿过障碍物的任何一条路径，设其分别于OE 和OF 的延长线交与P 、Q 两点，记A 和P 之间的路径长度为，显然>|AP|,又由AE ⊥EO,

所以|AP|>AE,从而>AE,同理可得>BF 。 再来比较PQ 之间路径长度和圆弧EF 的长度的大小。若PQ 之间的路径可

有极坐标方程

,则有,可得：

=≥-3π-

亦即路径APQB 的长度超过路径AEFB 的长度。以上证明足以说明了AEFB 是满足条件A 到B 的最短路径。

5.2 模型准备一

有了4.1中的定理，我们就可以这样认为，起点到目标点无论中间障碍物有多少，最短路径都应该是若干个线圆结构所组成。在本题中存在障碍物的状况，且障碍物在拐点处的危险区域是一个半径为1的圆弧，所以结合定理一，我们易知，求两点之间的最短路径中的转弯半径我们应该按照最小的转弯半径来算才能达到最优。

线圆结构5.21

1）如上图，设A （为起点，B （为目标点，C （和D （分别为机器人经过拐点分别于隔离危险线拐角小圆弧的切点，圆心为O （，圆的半径为r ，AB 的长度为a ，AO 的长度为b ，BO 的长度为c ，

角度AOB ∠=, AOC ∠=, BOD ∠=，COD θ∠=

.求A

B 的长度，设为L.

解法如下：

如上图可得有以下关系：

a b c ?=??=??=??

AOB ?在中：

在Rt AOC ?： =arccos r b β

在Rt AOC ?中：

arccos r

c γ=

所以：

2θπαβγ=---

从而可得：

L r θ=

2）而对于下图两种情况我们不能直接采用线圆的结构来解决，需要做简单的变换。

情况一：

222arccos()2b c a bc

α+-=

线圆结构5.22

我们假设两圆心坐标分别为11(,)O x y 和22(,)O x y ',半径均为r ，M 点坐标为33(,)x y ，那么我们很容易可以求得:

12312

322

x x x y y y +?=???+?=?? 这样我们就可以利用1）中的方法，先求A 到M ，再求M 到B ，这样分两段就可以求解。同理如果有更多的转弯，我们同样可以按照此种方法分解。

情况二：

线圆结构5.23

这里我们依然设圆心坐标分别为11(,)O x y 和22(,)O x y ',半径均为r ，这样我们可以得到：

2121

OO y y K x x '-=- 那么OO '直线方程为：

11()OO y K x x y '=-+

因为公切线DE 与OO '平行，那么DE 的直线方程可以表示为：

11()OO y K x x y C '=-++

其中：

C =

那么把公切线的方程于圆的方程联立，渴可以求得切点D 和E 的坐标。这样用D 和E 任意一点作为分割点都可以将上图分割成两个4.21所示的线圆结构，这样就可以对其进行求解。同理多个这样的转弯时，用同样的方法可以进行分割。

5.3 模型准备二

一、对于从起点经过若干点然后再到达目标点的状况，因为不能走折线路径，我们就必须考虑在经过路径中的一个目标点时转弯的状况。为了研究这个问题的方便，我们先来证明一个猜想：

猜想二:如果一个圆环可以绕着环上一个定点转动，那么过圆环外两定点连接一根绳子，并以该圆环为支撑拉紧绳子，达到平衡状态时，圆心与该顶点以及两条切线的延长线的交点共线。

图5.31

证明猜想：

如图4.31所示，E 点就是圆环上的一个顶点，A B 就是拉紧的绳子，2O 就是切线AC 和BD 的延长线的交点，证明1O 、E 、2O 三点共线。

我们可以用力学的知识进行证明，因为是拉紧的绳子，所以两边的绳子拉力

相等，设为F ，它们的合力设为0F ，定点对圆环的作用力设为1F 。

那么由几何学的知识我们可以知道0F 一定与12O O 共线，而又由力的平衡条

件可知：

0F =-1F

即12O O 与2EO 共线。

综上所述1O 、E 和2O 三点一定共线。

二、有了以上这个定理我们可以建立以下模型：

如图4.32，要求求出机器人从A 绕过障碍物经过M 点到达目标点B 的最短路径，我们采用以下方法：

用一根钉子使一个圆环定在M 点，使这个圆环能够绕M 点转动。然后连接A 和B 的绳子并以这些转弯处的圆弧为支撑（这里转弯处圆弧的半径均按照最小转弯半径来计算），拉紧绳子，那么绳子的长度就是A 到B 的最短距离。我们可以把路径图抽象为以下的几何图形。下面我们对这段路径求解：

图5.32

如图，A 11(,)x y 是起点，B 22(,)x y 是终点，1O 33(,)x y 和3O 44(,)x y 是两个固定的圆，2O 是一个可以绕M(p ，q)点转动的圆环，三个圆的半径均为r ，C 、D 、E 、F 、G 、H 均为切点。a 、b 、c 、e ，f 分别是A 1O 、1O 2O 、A 2O 、A 3O 、23O O 的长度。A 、B 、1O 、3O 均是已知点，2O 是未知点。那么最短路径就可以表示为： L=|AC|++|DE|++|FG|++|HB|

因为2O 点的坐标未知，所以我们就不能用模型一中的线圆结构对其进行求解。

故得先求出2O 点的坐标。设2O 坐标为（m ，n ），1A O C ∠、12AO O ∠、21AO O ∠、

23AO O ∠、32O O F ∠分别为i α（i =1、2、3、4、5）

，1C O D ∠、2EO F ∠、2EO M ∠分别为1θ、2θ、θ。这样便有以下关系：

a b c e f ?=??=??=

??=

??=??

在1Rt AOC ?中： 1arccos r a

α=

在12AO O ?中： 222

2arccos 2a b c ab

α+-= 222

3arccos 2b c a bc

α+-= 在23AO O ?中：

222

4arccos 2c f e cf

α+-= 在2Rt NO F ?中：

52arccos

r f

α= 则： 11223453232

πθααπθααα?=--????=---?? 又因为2MO 一定会在2EO F ∠的角平分线上，所以满足：

2

2θθ=

2θ我们采用向量的形式来求，易知12O O 的一个方向向量：

212(1,)y m x n

l -=- 而2O E 与12O O 垂直，故其一个方向向量：

222(1,)x n l y m

-=-- 而：

2(,)O M p m q n =--

所以：

2222ar ccos ||||l O M l O M θ?= 综合以上式子可以求得2O 的坐标，从而可以得出路径的长为：

120L r b r l θθ=+++ 0l =+HB ，这可以采用模型一中的线圆结构来求解。

5.4 模型准备三

求解从起点经过若干个点再到达目标点的问题，与4.4不同，我们还可以有另一种方案，即适当扩大障碍物拐点处的拐弯半径使机器人能够沿直线通过路径中的目标点。这样拐点处拐弯圆弧的半径和圆心都是个变量，对于该题，那么我们可以首先设定三个圆心1O 、2O 、3O ,然后按照以下步骤进行作图：

1） 给定1R ，以1O 为圆心，1R 为半径，画圆，然后过R 点做圆1O 的切线1L ，切

点为D 。然后过A 点做1O 的切线设为2L ，切点为E 。

2） 然后做2O F 垂直于2L ，垂足为F ，2O F 的长就是2R ，然后以2O 为圆心，2R 为

半径画圆。很显然2R 能由1R 来确定，即21=f(R )R 。

3） 然后过B 点做2O 的切线为3L ，切点为G ，再过3O F 垂直于3L ，垂足为H ，那

么3O H 的长度就是3R ，然后以3O 为圆心，3R 为半径，画圆。很显然3R 能

由2R 来确定，即3R =2f(R )。

4） 过C 做3O 的切线。这就完成了由R 经过A 和B 在到达C 的路径。

5） 然后再变换1O 、2O 、3O 、1R 、2R 、3R ，可得到新的路径。找出最小者即可。

5.5 模型的建立

假设机器人从起点R 到到目标点0M ，由4.2知路径一定是由圆弧和线段组成，设有m 条线段，n 条圆弧。那么目标函数可以表示为：

11

min m n

i j i j L d l ===+∑∑

11.r k s t ≥??≥?

= 用此模型就可以对起点到目标点之间的路径进行优化求解。

六、模型的求解

6.1 问题一

一、以下给出了R 到个目标点的可能路径的最短路径：

1）如图一，解决的就是R 到目标点A 的最短路径问题，很显然的一个问题是机器人从的上方走的最短路径肯定是大于机器人从下方走的最短路径，

所以机器人从方向走的最优路线我们在图一中没有给出。图一中，蓝线就可以为机器人隔出了危险区域，红线表示的就是通过

点的圆为支撑而拉紧的绳子，这样计算出绳子的长度就是R 到A 的最短路径。

2）如图二，解决的是R 到目标点B 的最短路径问题，图中给出了可能的三条路径的最短路径（图中的红线所示），我们可以分别计算出三条可能路径的最短路径的长度，然后进行比较，取最小者就是R 到目标点B 的最优路径。

3)如图三，解决的是R 到目标点C 的最短路径问题。图中给出了两条可能路径的最短路径（图中的红线所示），我们同样可以分别计算出两条可能的最短路径，取最小者就是R 到目标点C 的最优路径。

图5.11

图6.12

图6.13

二、然后用matlab求解

结果如下：

1)R到目标点A的最短距离为70.5076

2)R到目标点B的可能路径有三条，即就有三条可能的最短路径。

①如图二，机器人走最

上面这条路径到达B，直接用matlab求得最短路径为114.1611

②而机器人经过中间

一条路径到达B,这条路径由三条线段和两段圆弧组成，直接用三中

的解法是结不出来的。于是我们做了如下变换，先求出中间一条直线

的中点设为F，那么可以采用三中的解法，分别求R到F和F到B

的最短路径，然后两段相加，便可求出R到B的最短路径。求解结

果为107.9587

③机器人经过最下边

一条路径，同理这条路径由四条直线和三个圆弧组成，同样可以采取

②中的变换，分三部分求解。求解结果如下为116.1256

综合①②③所述，R到目标点B的最短路径为107.9587 3）R到目标点C的可能路径由两条，和2中的方法一样，最终求解结果R 到目标点C的最短路径为102.0514

6.2 问题二

一、我们先按照4.3中的思想来进行求解，这样我们可以做出5.21所示的

示意图：

图6.21

采用模型准备二中的计算方法，用lingo求解的结果最短路径为：156.471 二、我们在采用模型准备三中的算法进行求解，可以画出5.22所示的示意图：

图5.22

采用模型进行优化，运用lingo求解的最短路径为：157.752

显然运用模型准备二中的方法求解的结果小于用模型准备三中的方法求解的结

果，说明模型准备二的方法优于模型准备三的方法。

七、模型推广

7.1问题深入分析

在本题中只有四个障碍物，按照线圆结构画出从起点到达目标点的路径是有限的，我们完全可以采用穷举法把这些路径列出来，然后比较大小取最小者即可，但是我们可以设想如果这个区域内有n个障碍物，那么按照线圆结构从起点到达目标点的可能路径就有无数多条，这时我们如果在采用穷举法是不现实的。所以我们必须寻求新的算法来解决这个问题。

由上述分析我们有了这样一个想法：先求出所有的切线，包括出发点和目标点到所有圆弧的切线以及所有圆弧与圆弧之间的切线，然后把这且曲线看成是图6.11中的，给这些定点赋一个等于切线长度的权值，如果某两条切线有一个公切圆弧，则代表这两条曲线的顶点是一条直线的两个端点，边上的权值等于这两条切线之间的劣弧长度。然后在这张图中加一个源点和终点，那么在所有代表出发点与其它圆弧之间切线的顶点与源点连成一条边，权值均为0，同理在所有代表目标点到其它圆弧切线的顶点与终点连成一条边，权值均为0，这样题目就转化成了求源点到达终点之间的最短路径问题了，这里最短路径就是指经过所有顶点与边的权值之和最小。我们可以采用Dijkstra算法进行求解。

7.2 模型的进一步求解

根据6.1的分析，在有若干个障碍物的区域中，我们把按照线圆结构画出从出发点到目标点的路径图依据6.1中的想法转换成了下面这张图，图中的A和G 点就是添加的源点和终点，其它节点均是出发点和目标点到圆弧的切线和圆弧与圆弧之间的切线转化而成。

图7.21

对于最短路径的求解，有以下步骤：

1）我们画出出发点和目标点和各个圆弧的切线，以及圆弧与圆弧之间的切线，但是切线有可能经过障碍物的内部或危险区域，也可能出现切线重复的状况，既有很多不合法的切线。于是我们对模型做了以下修正：

1、 检验切线两个端点是否在障碍物内部。

2、 检验切线是否障碍物的对角线相交。

3、 检验圆弧所对应的圆心，即障碍物的顶点到切线的距离是否小于1。

如果以上三种情况满足其一，我们规定对应这段切线的顶点为M （M 为无穷大）。

4、 另外还有如下图所示的一种特殊情况：

两个大小相同在同一水平或者竖直位置上，不考虑切线满足1、2、3的状况它们由2条内公切线，8条外公切线，但是有6条外公切线是重复的。因此我们作如下规定:如果某条切线与某段圆弧相切，且切点不在切线的端点上，则该切线为不合法。权值矩阵中表示它的顶点也为M 。

图7.22

2） 然后把合法的切线与这些切线之间的劣弧转化成如7.21所示的形式。假设转化过后有m 条合法切线，那么就有m 个顶点，设这些点的权值i E （1i m ≤≤），即第i 条合法曲线的长度。j D 为边的权值，即第j 条弧的长度。

3）然后把路径图转化成如图6.21所示，按照求得权值矩阵给图中的顶点及边

长赋值。

4）最后依据Dijkstra 算法求得最短路径。

八、模型评价

一、模型优点 1、运用多个方案对路径进行优化，在相对优化之中取得最优解。

2、模型优化后用解析几何进行求解，精确度较高。

3、模型简单易懂，便于实际检验及应用。

二、模型缺陷

1、此模型适于全局规划，获得精确解却失去了效率。

2、在障碍物较多时，且形状不规则时，模型需要进一步改进。

九、参考文献

[1]谭永基，数学模型，上海，复旦大学出版社，2011

[2]邦迪，图论及其应用，西安，西安科学出版社 1984

[3]胡海星，RPG游戏中精灵的移动问题，杂志《程序员》 2011；

[4]尤承业，解析几何，北京，北京大学出版社，2004

[5]周培德，计算几何—算法与设计，北京清华大学出版社，2005

十、附录

1）%求解一次转弯所经路线总长

%T：初始点 V:转弯圆弧圆心 W:到达点

function result=zongchang(T,W,V,r)

TV=sqrt((T(1)-V(1))^2+(T(2)-V(2))^2);

TW=sqrt((T(1)-W(1))^2+(T(2)-W(2))^2);

VW=sqrt((V(1)-W(1))^2+(V(2)-W(2))^2);

alpha1=acos((TV^2+VW^2-TW^2)/(2*TV*VW));

alpha2=acos(r/TV);

alpha3=acos(r/VW);

alpha4=2*pi-alpha1-alpha2-alpha3;%alpha4为转弯圆心角

TS1=sqrt(TV^2-r^2);%TS1,TS2均为圆弧切线%

S2W=sqrt(VW^2-r^2);

S1S2hu=r*alpha4;

result=TS1+S1S2hu+S2W;

2）%判定是否经过路障,采用跨立实验（计算几何算法）

function m=intersect(H1,H2,G1,G2)

if

min(H1(1),H2(1))<=max(G1(1),G2(1))&min(G1(1),G2(1))<=max(H1(1),H2(1)) &min(G1(2),G2(2))<=max(H1(2),H2(2))&min(H1(2),H2(2))<=max(G1(2),G2(2) )&((G1(1)-H1(1))*(H2(2)-H1(2))-(H2(1)-H1(1))*(G1(2)-H1(2)))*((H2(1)-H 1(1))*(G2(2)-H1(2))-(H2(2)-H1(2))*(G2(1)-H1(1)))>=0

m=1;

else

if

(abs((G2(2)*H2(1)-G2(2)*G1(1)-G1(2)*H2(1)+G1(1)*G1(2))/(G2(1)-G1(1))+ G1(2)-H2(2)))/(sqrt(1+(G2(2)-G1(2))^2/(G2(1)-G1(1))^2))<=1%保证障碍圆弧部分不与两点连线相切

m=1;

else

m=0;

end

3）%求解R经过中间节点到达目标点的最短路径

model:

min=d1+b+d3+u+v+t;

a=@sqrt(40^2+15^2);

b=@sqrt((x1-40)^2+(y1-15)^2);

c=@sqrt(x1^2+y1^2);

d1=3*3.1415926/2-@acos((a^2+b^2-c^2)/(2*a*b))-@acos(1/a);

(x1-50)^2+(y1-40)^2=1;

x1>49;

x1<50;

d2=@acos(@abs((50-x1+(1600-40*x1-40*y1+x1*y1)/(y1-15))/(@sqrt(1+(x1-4 0)^2/(y1-15)^2)*@sqrt((50-x1)^2+(40-y1)^2))));

e=@sqrt(55^2+55^2);