弹性力学简明教程-第四章-平面问题的极坐标解答习题详解

第四章 平面问题的极坐标解答
典型例题讲解
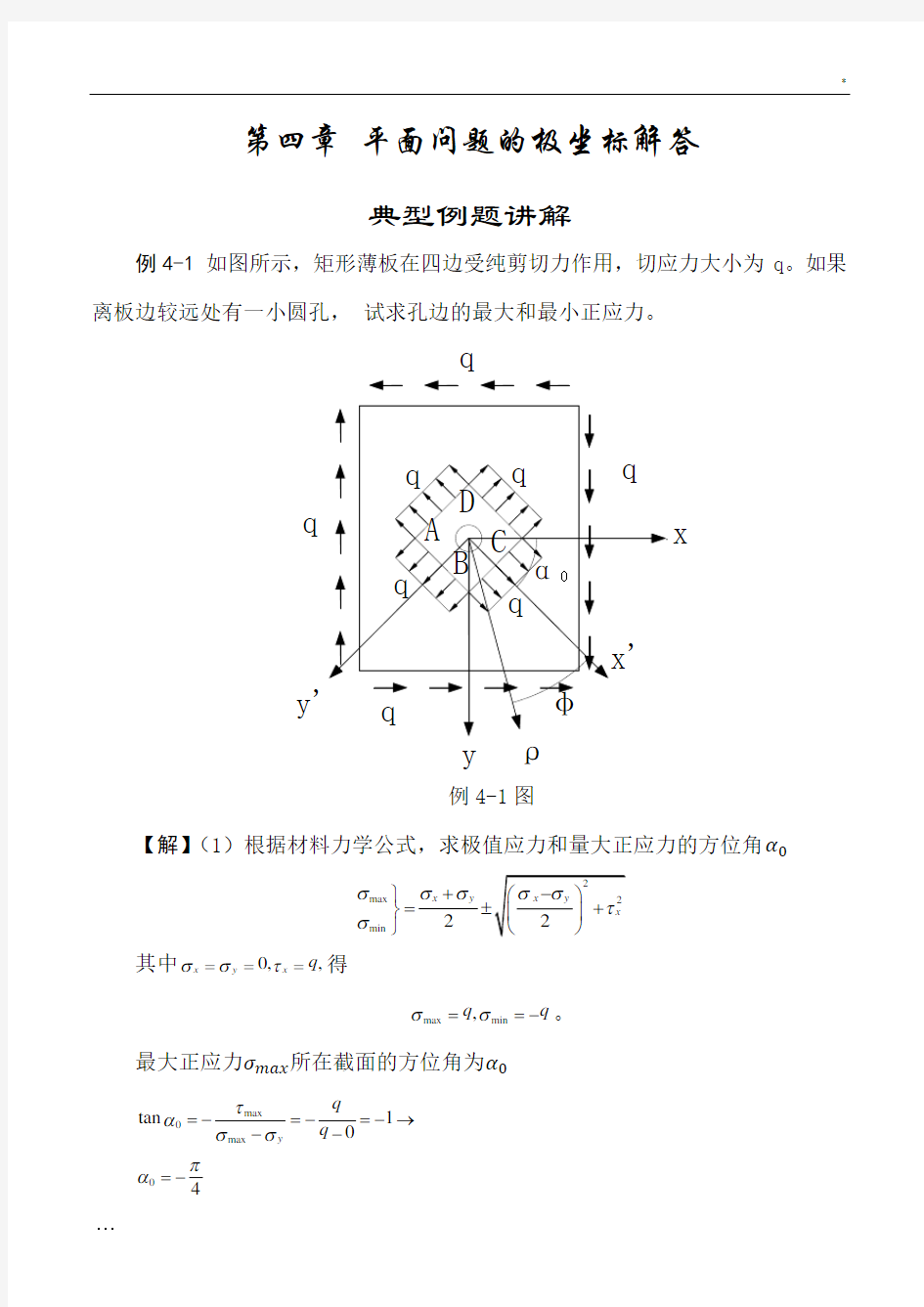
例4-1 如图所示,矩形薄板在四边受纯剪切力作用,切应力大小为q 。如果离板边较远处有一小圆孔, 试求孔边的最大和最小正应力。
例4-1图
【解】(1)根据材料力学公式,求极值应力和量大正应力的方位角α0
max min 2x y σσσσ+?=??其中0,,x y x q σστ===得
max min ,q q σσ==-。
最大正应力σmax 所在截面的方位角为α0
max 0max 0tan 10
4
y
q
q τασσπ
α=-
=-
=-→--=-
q
q
x
若在该纯剪切的矩形薄板中,沿与板边成π
4
方向截取矩形ABCD ,则在其边界
上便承受集度为q 的拉力和压力,如图所示。这样就把受纯剪切作用的板看作与一对边受拉,另一对边受压的板等效。
(2)取极坐标系如图。由
2222442222cos 2(1)(13),cos 2(13),(4-18)sin 2(1)(13).ρφρφr r σq φρρr σq φρr r τq φρρ?
=--?
?
??
=-+?
??
=--+?
??
得矩形薄板ABCD 内的应力分量为
()()()
22
224
422
22cos 2(1)(13)
cos 2(13)
sin 2(1)(13)
ρφρφ
a a σq φa ρρa σq φ
b ρa a τq φ
c ρρ
=--=-+=--+ 其中α为小孔的半径,而孔边最大与最小正应力由式(b ),在ρ=α处得到
4
4cos 2(13)4cos 2,φa σq φa
?=-+=-
当φ=0,π时,孔边最小正应力为(σφ)
min
=?4q ,
当φ=±π
2时,孔边最大正应力为(σφ)max
=4q 。
分析:矩形板ABCD 边界上各点的应力状态与板内无孔时的应力状态相同。也可以应用叠加法,求解薄板的各种较复杂的平面应力(应变)问题。
习题全解
4-1试比较极坐标和直角坐标中的平衡微分方程、几何方程和物理方程,指出哪些项是相似的,哪些项是极坐标中特有的?并说明产生这些项的原因。
【解】 (1)极坐标,直角坐标中的平衡微分方程
10210f f ρρ?ρ?
ρρ??ρ??στσσρρ?ρτστρ
ρ?ρ??-?+++=????
?
???+++=???? 00
yx
x x y xy y
f x
y f y x τσστ???++=?
????
??++=????
将极坐标中的平衡微分方程与直角坐标中的平衡微分方程相比较,第一式中,前两项与直角坐标相似;而σρ
ρ项是由于正ρ面上的面积大于负ρ面上的面积而产生
的,?
σφρ
是由于正负φ面上的正应力σφ在通过微分体中心的ρ方向有投影而引起的。
第二式中,前两项也与直角坐标相似;而τρφρ
是由于正ρ面面积大于负ρ面上的面
记而产生的;
τφρρ
是由于正负φ面上的切应力τφρ在通过微分体中心的φ方向有投
影而引起的。由于τρφ=τφρ,仍可将这两个切应力只作为一个未知函数处理。
(2)极坐标,直角坐标中的几何方程
11u u u u u u ρρρ??
ρ??
ρ?ερερρ?γρ?ρρ??
=??????=+??????=+-?????
x y
xy
u x v
y v u x y εεγ??=
?????=??????=+????
将极坐标中的几何方程与直角坐标的几何方程相比较,第二式中的第一项
u ρρ
是在极坐标中才有的,表示由于径向位移而引起的环形线段的伸长应变;第三式
中的?
u φρ
是由于环向位移而引起的环向钱段的转角,这项也是在极坐标中才有的。
(3)极坐标,直角坐标中的物理方程
1()1()
12(1)E E G E ρρ???ρρ?ρ?
ρ?εσνσεσνσνγττ?
=-??
?
=-??
+?==??
()()()1121x x y y y x xy xy E E E
εσμσεσμσμγτ?
=-??
?
=-???+=?? 极坐标中的物理方程与直角坐标的物理方程是相似的。 4-2试导出极坐标和直角坐标中位移分量的坐标变换式。 【解】 参看图,位移矢量是服从几何加减 运算法则的。
位移矢量为d ,它在(x,y )和(ρ,φ)坐标系中的分量分别表示为(u,v )和(u ρ,u φ),所以
cos sin sin cos u u u u ρ?
?υ?
?υ?=+???
=-+?? 写成矩阵形式
cos sin sin cos u u u ρ????
?υ??????
=??????-??????
?? 解4-2图
所以
cos sin sin cos u u u ρ???υ????
-????=????????
???
??? 若写成一般形式,则位移分量的变换关系为
cos sin sin cos u u u v u u ρ?ρ?????=-???
=+??
或 cos sin sin cos u u v u u v ρ???
??
=+???=-+??
4-3在轴对称位移问题中,试导出按位移求解的基本方程。并证明u ρ=Aρ+
B ρ
,u φ=0可以满足此基本方程。
【解】(1)设u ρ=u ρ(ρ),u φ=0,代入几何方程中,教材中式(4-2)得
形变分量
,,0u u ρρ
ρ?ρ?εεγρρ
?=
=
=? (a )
将式(a )代入物理方程,教材中式(4-3)得用位移表示的应力分量
22110u u E u u E ρρρρρ?ρ?σμμρρσμμρρτ????
=+? ?-???
?????
?=+? ?-???
?
?=???
(b ) 将(b )式代入平衡微分方程,教材中式(4-1),在轴对称问题中,平衡方程为
10210ρρ?ρ?
?ρ?ρ??σ?τσσ?ρρ??ρ?σ?ττρ??
?ρρ-?++=??
?
?++=?? (c ) 式(c )中的第二式自然满足,第一式为
22222222221011011101u u d E d du u du u E E d d d u du du u du u u d d d d u d d u d d u d u u d ρρ?ρ?ρ
ρρρρρρρρ
ρρρρρρρρρ?σ?τσσμ?ρρ??ρρμρρ
μμρμρρμρρμμμμρρμμρρμμρρρρρρρ
ρρρρρ-???
??++=→+?? ?-?????
?-?
????++-+=→?? ? ?--???
?????+-++--=→ +++??-?222
2010u d u du u d du d d ρ
ρρρ
ρρ
ρρρρρρ
-=→+
-= 上式即为求u ρ的基本方程。
(2)将u ρ=Aρ+B
ρ,u φ=0代入式(d ),很显然满足方程。
4-4试导出轴对称位移问题中,按应力求解时的相容方程。
【解】(1)在轴对称的情况下,τρφ=τφρ=0,只有σρ,σφ为基本未知函数,且
它们仅为ρ的函数。几何方程,教材中式(4-2)的前二式成为
1u du d u u u ρρρρ?ρ?
ερρερρ?ρ??
==???
?
??=+=???
(a ) 对式(a )中的第二式求导,得
1,d du u d dx ?
ρρερρρ??
=- ???
(b ) 将式(a )中的ερ,εφ代入式(b ),得
()1
,d d ?ρ
?εεερ
ρ
=
- (c )
(2)将物理方程,教材中式(4-3)、(4-4)中的用应力分量表示的形变分量代入式(c )中,就得到按应力求解时的相容方程,即
平面应力的相容方程:
()()()1
1111()()()11
()()1()1()()d d d d E E E d d d d ?
ρ??ρρ??ρ?ρρ?ρ?ρ??ρρ?εε
εσμσσμσσμσρρ
ρρσμσσσμσσμσσρρρ
μσμσσσρρ
????
=-→
-=---→ ???????
????-=-+-=+-→????+-=- 平面应变的相容方程:
221()11()12(1)
E E E ρρ???ρρ?ρ?μμ
εσσμμμεσσμμγτ?-=-?
-??-?
=-?-?
?+=?
??
(4-4)
()()()2221
1111()()()1111111()()1()()11111()(11d d d d E E E d d d d ?
ρ??ρρ??ρ?ρρ?ρ?ρ?ρ??ρρεμμμμμμ
εεσσσσσσρρρμρμμμμμσσσσσσσσσσρμρμρμρμμσσσρμρμ????---=-→-=---→ ???---????
??????????-=-+-=+-=-→???? ? ???----??????????-=--())()1d d ?ρ??ρσσσμσμσρρ
-→-??--=??4-5试用一阶导数的坐标变换式,导出二阶导数的坐标变换式[教材§4-3中的(a ),(b ),(c )]
【解】一阶导数的坐标变换公式
1
()1()12(1)E E G E
ρρ???ρρ?ρ?ρ?
εσνσεσνσνγττ=
-=-+==(4-3)
sin cos cos sin x x x y y y ΦΦρΦ?Φ?
Φ
?ρ?ρρ?ΦΦρΦ?Φ?
Φ?ρ?ρρ?
???????=?+?=-??????????????=?+?=+??????? 二阶导数的变换可以由一阶导数得出
22
22
222222
sin sin ()(cos )(cos )sin sin sin cos (cos )(cos )
1cos s 11sin cos sin c 1s in o in cos 1sin cos s x x x ΦΦ?Φ?Φ
??ρρ?ρρ?
Φ?Φ?Φ?Φ
???ρρρ?ρ?ρΦΦ????
ρρ?ρρρ?
ΦΦ??
?ρΦ??ρ?ρ?ρρ????????==--???????????--???????=---????????=+???+?+?22
2
2
222
22
22
2
222
2
222222
22222
221sin 11cos sin sin 1112s cos sin 11cos 12sin co si in cos 12sin s c n os 1Φ?ρρΦΦΦ??Φ??ρρρρρΦΦΦ??ρρρρΦ?Φ??ρ?ρρ?ΦρΦΦΦ??ρρ?Φ??ρ?ρρ?ρρ?+????=++????????=++- ?????????=+?-??+?????+????-+ ????
????22sin cos 1?Φρ?ρ?ρ??????? ????- ?????
????(a )
22
22
22222cos cos 1sin cos ()s 11sin cos si in sin cos cos cos sin sin sin s 1co i c s s o n n y y y ΦΦ?Φ?Φ??ρρ?ρρ?Φ?Φ?Φ?Φ???ρρρ?ρΦ??ρΦΦ????
ρρΦ?ρρ?ρρρ????Φρ?????
???????==++ ??????????????
????
??????=+++ ?
?????????+???-+???=?????+22
2
2
222
22222
22
2
22
222
222
22222
22
1cos 1112sin cos 12sin c cos cos 11c sin sin 1sin cos 12sin cos os 1co 1i os s s n Φ?ρ?ΦΦ??ρρρ?ΦΦ?ρ?Φ??ρ?Φ??ρ?ρρρΦ??ρ?Φ????Φ?ρΦ?ρΦ?ρ?ρρΦ??=??=????+????+ ????+???++???????++ ?????+?-??-??-??
=?222112sin cos ?ΦΦ?ρΦρρ?ρ?ρ?????+?? ??????+ ????????
???(b )
弹性力学简明教程(第四版)_课后习题解答
弹性力学简明教程(第四版)课后习题解答 徐芝纶 第一章绪论 1、试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体? 【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各 向异性体,就是不满足均匀性假定,但满足各向同性假定。 【解答】均匀的各项异形体如:竹材,木材。 非均匀的各向同性体如:混凝土。 1.2 一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体? 【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性, 各向同性假定。 【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和 岩质地基不可以作为理想弹性体。 1.3五个基本假定在建立弹性力学基本方程时有什么作用? 【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。引用这一假定后,物体的应力、形变和位移等物理 量就可以看成是连续的。因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。 均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。 各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。 小变形假定:假定位移和变形是微小的。亦即,假定物体受力以后整个物体所有各点的 位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。这样在建立物体变形以后的 平衡方程时,就可以方便的用变形以前的尺寸来代替变形以后的尺寸。在考察物体的位移与 形变的关系时,它们的二次幕或乘积相对于其本身都可以略去不计,使得弹性力学中的微分
弹性力学概念汇总
1、五个基本假定在建立弹性力学基本方程时有什么用途? 答:连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可以看成是连续的,因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 完全弹性假定:引用这一完全弹性的假定还包含形变与形变引起的正应力成正比的含义,亦即二者成线性的关系,符合胡克定律,从而使物理方程成为线性的方程。 均匀性假定:在该假定下,所研究的物体内部各点的物理性质显然都是相同的。因此,反映这些物理性质的弹性常数(如弹性模量E和泊松比μ等)就不随位置坐标而变化 各向同性假定:所谓“各向同性”是指物体的物理性质在各个方向上都是相同的。进一步地说,就是物体的弹性常数也不随方向而变化。 小变形假定:我们研究物体受力后的平衡问题时,不用考虑物体尺寸的改变而仍然按照原来的尺寸和形状进行计算。同时,在研究物体的变形和位移时,可以将他们的二次幂或乘积略去不计,使得弹性力学中的微分方程都简化为线性微分方程。 在上述假定下,弹性力学问题都化为线性问题,从而可以应用叠加原理。 2、试分析简支梁受均布荷载时,平面截面假设是否成立? 解:弹性力学解答和材料力学解答的差别,是由于各自解法不同。简言之,弹性力学的解法,是严格考虑区域内的平衡微分方程,几何方程和物理方程,以及边界上的边界条件而求解的,因而得出的解答是比较精确的。而在材料力学中没有严格考虑上述条件,因而得出的是近似解答。例如,材料力学中引用了平面假设而简化了几何关系,但这个假设对一般的梁是近似的。所以,严格来说,不成立。 3、为什么在主要边界(占边界绝大部分)上必须满足精确的应力边界条件,教材中式(2-15),而在次要边界(占边界很小部分)上可以应用圣维南原理,用三个积分的应力边界条件(即主矢量、主矩的条件)来代替?如果在主要边界上用三个积分的应力边界条件代替教材中式(2-15),将会发生什么问题? 解:弹性力学问题属于数学物理方程中的边值问题,而要边界条件完全得到满足,往往遇到很大的困难。这时,圣维南原理可为简化局部边界上的应力边界条件提供很大的方便。将物体一小部分边界上的面力换成分布不同,但静力等效的面力(主矢、主矩均相同),只影响近处的应力分布,对远处的应力影响可以忽略不计。如果在占边界绝大部分的主要边界上用三个应力边界条件来代替精确的边界条件。教材中式(2-15),就会影响大部分区域的应力分布,会使问题的解答具有的近似性。 4、在导出平面问题的三套基本方程时,分别应用了哪些基本假定?这些方程的适用条件是什么? 答:1、在导出平面问题的平衡微分方程和几何方程时应用的基本假定是:物体的连续性,小变形和均匀性。在两种平面问题中,平衡微分方程和几何方程都适用。2、在导出平面问题的物理方程时应用的基本假定是:物体的连续性,完全弹性,均匀性,小变形和各向同性,即物体为小变形的理想弹性体。在两种平面问题中的物理方程不一样,如果将平面应力问题的物理方程中的E换为换为,就得到平面应变问题的物理方程。 5、简述材料力学和弹性力学在研究对象、研究方法方面的异同点。 在研究对象方面,材料力学基本上只研究杆状构件,也就是长度远大于高度和宽度的构件;而弹性力学除了对杆状构件作进一步的、较精确的分析外,还对非杆状结构,例如板和壳,以及挡土墙、堤坝、地基等实体结构加以研究。在研究方法方面,材料力学研究杆状构件,除了从静力学、几何学、物理学三方面进行分析以外,大都引用了一些关于构件的形变状态或应力分布的假定,这就大简化了数学推演,但是,得出的解答往往是近似的。弹性力学研究杆状构件,一般都不必引用那些假定,因而得出的结果就比较精确,并且可以用来校核材料力学里得出的近似解答。另一份答案:弹力研究方法:在区域V内严格考虑静力学、几何学和物理学三方面条件,建立平衡微分方程、几何方程和物理方程;在边界s上考虑受力或约束条件,并在边界条件下求解上述方程,得出较精确的解答。 在研究内容方面:材料力学研究杆件(如梁、柱和轴)的拉压、弯曲、剪切、扭转和组合变形等问题;结构力学在
弹性力学试题参考答案与弹性力学复习题
弹性力学复习资料 一、简答题 1.试写出弹性力学平面问题的基本方程,它们揭示的是那些物理量之间的相互关系在应用这些方程时,应注意些什么问题 答:平面问题中的平衡微分方程:揭示的是应力分量与体力分量间的相互关系。应注意两个微分方程中包含着三个未知函数σx、σy、τxy=τyx ,因此,决定应力分量的问题是超静定的,还必须考虑形变和位移,才能解决问题。 平面问题的几何方程: 揭示的是形变分量与位移分量间的相互关系。应注意当物体的位移分量完全确定时,形变量即完全确定。反之,当形变分量完全确定时,位移分量却不能完全确定。 平面问题中的物理方程:揭示的是形变分量与应力分量间的相互关系。应注意平面应力问题和平面应变问题物理方程的转换关系。 2.按照边界条件的不同,弹性力学问题分为那几类边界问题试作简要说明。 答:按照边界条件的不同,弹性力学问题分为位移边界问题、应力边界问题和
混合边界问题。 位移边界问题是指物体在全部边界上的位移分量是已知的,也就是位移的边界值是边界上坐标的已知函数。 应力边界问题中,物体在全部边界上所受的面力是已知的,即面力分量在边界上所有各点都是坐标的已知函数。 混合边界问题中,物体的一部分边界具有已知位移,因而具有位移边界条件;另一部分边界则具有应力边界条件。 3.弹性体任意一点的应力状态由几个应力分量决定试将它们写出。如何确定它们的正负号 答:弹性体任意一点的应力状态由6个应力分量决定,它们是:x 、y 、z 、xy 、yz 、、zx 。正面上的应力以沿坐标轴正方向为正,沿坐标轴负方向为负。负面上的应力以沿坐标轴负方向为正,沿坐标轴正方向为负。 4.在推导弹性力学基本方程时,采用了那些基本假定什么是“理想弹性体”试举例说明。 答:答:在推导弹性力学基本方程时,采用了以下基本假定: (1)假定物体是连续的。 (2)假定物体是完全弹性的。 (3)假定物体是均匀的。 (4)假定物体是各向同性的。 (5)假定位移和变形是微小的。 符合(1)~(4)条假定的物体称为“理想弹性体”。一般混凝土构件、一般土质地基可近似视为“理想弹性体”。 5.什么叫平面应力问题什么叫平面应变问题各举一个工程中的实例。 答:平面应力问题是指很薄的等厚度薄板只在板边上受有平行于板面并且不沿厚度变化的 面力,同时体力也平行于板面并且不沿厚度变化。如工程中的深梁以及平板坝的平板 支墩就属于此类。 平面应变问题是指很长的柱型体,它的横截面在柱面上受有平行于横截面而且不沿长 度变化的面力,同时体力也平行于横截面而且也不沿长度变化,即内在因素和外来作 用都不沿长度而变化。 6.在弹性力学里分析问题,要从几方面考虑各方面反映的是那些变量间的关系 答:在弹性力学利分析问题,要从3方面来考虑:静力学方面、几何学方面、物理学方面。 平面问题的静力学方面主要考虑的是应力分量和体力分量之间的关系也就是平面问 题的平衡微分方程。平面问题的几何学方面主要考虑的是形变分量与位移分量之间的 关系,也就是平面问题中的几何方程。平面问题的物理学方面主要反映的是形变分量与应力分量之 间的关系,也就是平面问题中的物理方程。 7.按照边界条件的不同,弹性力学平面问题分为那几类试作简要说明 答:按照边界条件的不同,弹性力学平面问题可分为两类: (1)平面应力问题 : 很薄的等厚度板,只在板边上受有平行于板面并且不沿厚度变化的面力。这一类问题可以简化为平面应力问题。例如深梁在横向力作用下的受力分析问题。在该种问题中只存在 yx xy y x ττσσ=、、三个应力分量。 (2)平面应变问题 : 很长的柱形体,在柱面上受有平行于横截面并且不沿长度变化的面力,而且体力
弹性力学简明教程(第四版)_习题解答
【2-9】试列出图2-17,图2-18所示问题的全部边界条件。在其端部小边界上,应用圣维南原理列出三个积分的应力边界条件。 x y 2 h 1h b g ρo () 2h b >> h x y l /2/2 h M N F S F 1 q q 图2-17 图2-18 【分析】有约束的边界上可考虑采用位移边界条件,若为小边界也可写成圣维南原理的三个积分形式,大边界上应精确满足公式(2-15)。 【解答】图2-17: 上(y =0) 左(x =0) 右(x =b ) l 0 -1 1 m -1 () x f s () 1g y h ρ+ () 1g y h ρ-+ () y f s 1gh ρ 代入公式(2-15)得 ①在主要边界上x=0,x=b 上精确满足应力边界条件: ()()100(),0;===-+=x xy x x g y h σρτ ()()1b b (),0; ===-+=x xy x x g y h σρτ ②在小边界0y =上,能精确满足下列应力边界条件: () () ,0y xy y y gh σρτ===-= ③在小边界2y h =上,能精确满足下列位移边界条件: ()()2 2 0,0 ====y h y h u v 这两个位移边界条件可以应用圣维南原理,改用三个积分的应力边界条件来代替,当板厚=1δ时,可求得固定端约束反力分别为: 10,,0s N F F gh b M ρ==-=
由于2y h =为正面,故应力分量与面力分量同号,则有: ()()()222 10000 0b y y h b y y h b xy y h dx gh b xdx dx σρστ===?=-???=???=????? ⑵图2-18 ①上下主要边界y=-h/2,y=h/2上,应精确满足公式(2-15) l m x f (s) y f (s) 2h y =- 0 -1 0 q 2 h y = 1 -1q -/2()y y h q σ==-,-/2()0yx y h τ==,/2()0y y h σ==,/21()yx y h q τ==- ②在x =0的小边界上,应用圣维南原理,列出三个积分的应力边界条件:负面上应力与面力符号相反,有 /20/2/2 0/2/20 /2()()()h xy x S h h x x N h h x x h dx F dx F ydx M τσσ=-=-=-?=-??=-???=-???? ③在x=l 的小边界上,可应用位移边界条件0,0====l x l x v u 这两个位移边界条件也可改用三个积分的应力边界条件来代替。 首先,求固定端约束反力,按面力正方向假设画反力,如图所示,列平衡方程求反力: 110,x N N N N F F F q l F q l F ''=+=?=-∑ 0,0y S S S S F F F ql F ql F ''=++=?=--∑ 2 211110,'02222 A S S q lh ql M M M F l ql q lh M M F l =+++-=?=---∑ 由于x=l 为正面,应力分量与面力分量同号,故 M ' N F 'S F '
清华大学弹性力学讲义chap2_Elasticity of Solids
2.Elasticity of Solids References J.H.Weiner ,Statistical mechanics of elasticity, Wiley, 1981 Green & Zerna ,Theoretical elasticity, 1968 Ashby & Jones ,Engineering materials 2.1 Definition of Elasticity Elasticity σ F Figure 2.1 An elastic response. An elastic response of the material can be abstracted mathematically as ()X F ,T σ= (2.1) where σ denotes the stress tensor, T the response function that depends only on the current values of the deformation gradient X x F ??=, with X denoting the material coordinates of a point while x the spatial coordinates. If the material is homogeneous within the domain under consideration, the explicit dependence on X in (2.1) can be eliminated. Several remarks can be made to the definition in (2.1): (1) In the claim of ()()X t X, F ,T σ=, one pins down an elastic response as the one prtrayed by the current status of deformation, and henceforth irrelevant to the
弹性力学习题(新)
1-3 五个基本假定在建立弹性力学基本方程时有什么用途? 答:1、连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可以看成是连续的,因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 2、完全弹性假定:引用这一完全弹性的假定还包含形变与形变引起的正应 力成正比的含义,亦即二者成线性的关系,符合胡克定律,从而使物理方程成为线性的方程。 3、均匀性假定:在该假定下,所研究的物体内部各点的物理性质显然都是 相同的。因此,反映这些物理性质的弹性常数(如弹性模量E和泊松比μ等)就不随位置坐标而变化。 4、各向同性假定:所谓“各向同性”是指物体的物理性质在各个方向上都是 相同的。进一步地说,就是物体的弹性常数也不随方向而变化。 5、小变形假定:我们研究物体受力后的平衡问题时,不用考虑物体尺寸的 改变而仍然按照原来的尺寸和形状进行计算。同时,在研究物体的变形和位移时,可以将他们的二次幂或乘积略去不计,使得弹性力学中的微分方程都简化为线性微分方程。 在上述假定下,弹性力学问题都化为线性问题,从而可以应用叠加原理。
2-1 已知薄板有下列形变关系:式中A,B,C,D皆为常数,试检查在形变过程中是否符合连续条件,若满足并列出应力分量表达式。 解: 1、相容条件: 将形变分量带入形变协调方程(相容方程)
其中 所以满足相容方程,符合连续性条件。 2、在平面应力问题中,用形变分量表示的应力分量为 3、平衡微分方程
其中 若满足平衡微分方程,必须有
分析:用形变分量表示的应力分量,满足了相容方程和平衡微分方程条件,若要求出常数A,B,C,D还需应力边界条件。 例2-2 如图所示为一矩形截面水坝, 其右侧面受静水压力(水的密度为ρ), 顶部受集中力P作用。试写出水坝的应 力边界条件。 解: 根据在边界上应力与面力的关系 左侧面:
弹性力学复习重点+试题及答案【整理版】
弹性力学2005 期末考试复习资料 一、简答题 1.试写出弹性力学平面问题的基本方程,它们揭示的是那些物理量之间的相互关系?在应用这些方程时,应注意些什么问题? 答:平面问题中的平衡微分方程:揭示的是应力分量与体力分量间的相互关系。应注意两个微分方程中包含着三个未知函数σx、σy、τxy=τyx ,因此,决定应力分量的问题是超静定的,还必须考虑形变和位移,才能解决问题。 平面问题的几何方程: 揭示的是形变分量与位移分量间的相互关系。应注意当物体的位移分量完全确定时,形变量即完全确定。反之,当形变分量完全确定时,位移分量却不能完全确定。 平面问题中的物理方程:揭示的是形变分量与应力分量间的相互关系。应注意平面应力问题和平面应变问题物理方程的转换关系。 2.按照边界条件的不同,弹性力学问题分为那几类边界问题? 试作简要说明。 答:按照边界条件的不同,弹性力学问题分为位移边界问题、应力边界问题和 混合边界问题。 位移边界问题是指物体在全部边界上的位移分量是已知的,也就是位移的边界值是边界上坐标的已知函数。 应力边界问题中,物体在全部边界上所受的面力是已知的,即面力分量在边界上所有各点都是坐标的已知函数。 混合边界问题中,物体的一部分边界具有已知位移,因而具有位移边界条件;另一部分边界则具有应力边界条件。 3.弹性体任意一点的应力状态由几个应力分量决定?试将它们写出。如何确定它们的正负号? 答:弹性体任意一点的应力状态由6个应力分量决定,它们是:x 、y 、z 、xy 、yz、、zx。正面上的应力以沿坐标轴正方向为正,沿坐标轴负方向为负。负面上的应力以沿坐标轴负方向为正,沿坐标轴正方向为负。 4.在推导弹性力学基本方程时,采用了那些基本假定?什么是“理想弹性体”?试举例说明。 答:答:在推导弹性力学基本方程时,采用了以下基本假定:(1)假定物体是连续的。 (2)假定物体是完全弹性的。 (3)假定物体是均匀的。 (4)假定物体是各向同性的。 (5)假定位移和变形是微小的。 符合(1)~(4)条假定的物体称为“理想弹性体”。一般混凝土构件、一般土质地基可近似视为“理想弹性体”。 5.什么叫平面应力问题?什么叫平面应变问题?各举一个工程中的实例。 答:平面应力问题是指很薄的等厚度薄板只在板边上受有平行于板面并且不沿厚度变化的 面力,同时体力也平行于板面并且不沿厚度变化。如工程中的深梁以及平板坝的平板 支墩就属于此类。 平面应变问题是指很长的柱型体,它的横截面在柱面上受有平行于横截面而且不沿长 度变化的面力,同时体力也平行于横截面而且也不沿长度变化,即内在因素和外来作 用都不沿长度而变化。 6.在弹性力学里分析问题,要从几方面考虑?各方面反映的是那些变量间的关系? 答:在弹性力学利分析问题,要从3方面来考虑:静力学方面、几何学方面、物理学方面。 平面问题的静力学方面主要考虑的是应力分量和体力分量之间的关系也就是平面问 题的平衡微分方程。平面问题的几何学方面主要考虑的是形变分量与位移分量之间的 关系,也就是平面问题中的几何方程。平面问题的物理学方 面主要反映的是形变分量与应力分量之间的关系,也就是平 面问题中的物理方程。 7.按照边界条件的不同,弹性力学问题分为那几类边界问题? 试作简要说明 答:按照边界条件的不同,弹性力学问题可分为两类边界问题:
弹性力学作业习题
HOMEWORK OF THEORETICAL ELASTICITY 1. DATE: 2001-9-20 1. 设地震震中距你居住的地方直线距离为l ,地层的弹性常数ν,E 和密度ρ均为已知。假 设你在纵波到达0t 秒后惊醒。问你在横波到达之前还有多少时间跑到安全地区试根据Km 200=l ,GPa 20=E ,3.0=ν,36g/m 100.2?=ρ,s 30=t 来进行具体估算。 2. 假定体积不可压缩,位移112(,)u x x 与212(,)u x x 很小,30u ≡。在一定区域内已 知22 12 11(1) ()u x a bx cx =-++,其中a ,b ,c 为常数,且120ε=,求212(,)u x x 。 3. 给定位移分量 21123()u cx x x =+,22213()u cx x x =+,23312()u cx x x =+,此处c 为一个很小的常数。求 应变分量ij ε及旋转分量ij Q 。 4. 证明 ,1 122 i ijk jk ijk k j e Q e u ω== 其中i ω为转动矢量。 5. 设位移场为22131232123()()u a x x e a x x e ax x e =-++-,其中a 为远小于1的常数。确定在 (0,2,1)P -点的小应变张量分量,转动张量分量和转知矢量分量。 6. 试分析以下应变状态能否存在。 (1)22111 22()k x x x ε=+,2 2223kx x ε=,330ε=,121232kx x x γ=,23310γγ== (2)22111 2()k x x ε=+,2222kx x ε=,330ε=,12122kx x γ=,23310γγ== (3)21112ax a ε=,22212ax x ε=,3312ax x ε=,120γ=,22332ax bx γ=+,22 3112ax bx γ=+ 其中,,k a b 为远小于1的常数。 2. DATE: 2001-9-17 1. 证明对坐标变换?? ? ?????????-=? ??? ??2121cos sin sin cos x x x x αααα ,33x x =,无论α为何值均有
弹性力学模拟练习题
一、判断题 1、连续性假定是指整个物体的体积都被组成这个物体的介质所填满,不留下任 何空隙。 (√) 2、如果某一问题中,0===zy zx z ττσ,只存在平面应力分量x σ,y σ,xy τ,且它 们不沿z 方向变化,仅为x ,y 的函数,此问题是平面应力问题。 (√) 3、如果某一问题中,0===zy zx z γγε,只存在平面应变分量x ε,y ε,xy γ,且它们 不沿z 方向变化,仅为x ,y 的函数,此问题是平面应变问题。 (√) 4、当物体的形变分量完全确定时,位移分量却不能完全确定。 (√) 5、当物体的位移分量完全确定时,形变分量即完全确定。 (√) 6、在有限单元法中,结点力是指结点对单元的作用力。 (√) 7、在平面三结点三角形单元的公共边界上应变和应力均有突变。 (√) 10、体力作用于物体部的各个质点上,所以它属于力。 (×) 解答:外力。它是质量力。 11、在弹性力学和材料力学里关于应力的正负规定是一样的。 (×) 解答:两者正应力的规定相同,剪应力的正负号规定不同。 12、当问题可当作平面应力问题来处理时,总有 0===yz xz z ττσ。 (√) 解答:平面应力问题,总有0===yz xz z ττσ 13、当物体可当作平面应变问题来处理时,总有 0===yz xz z γγε。 (√) 解答:平面应变问题,总有0 ===yz xz z γγε 14、已知位移分量函数() xy k v y x k u 2221,=+=,21,k k 为常数,由它们所求得形变分量不一定能满足相容方程。 (×) 解答:由连续可导的位移分量按几何方程求得的形变分量也一定能满足相 容方程。因为几何方程和相容方程是等价的。 15、形变状态()()0,2,,222≠==+=k kxy ky y x k xy y x γεε是不可能存在的。 (×) 解答:所给形变分量能满足相容方程,所以该形变分量是可能存在的。 16、在y 为常数的直线上,如0=u ,则沿该线必有0=x ε。 (√)
弹性力学简明教程(第四版)习题解答
弹性力学简明教程(第四版) 习题解答 第一章绪论 【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体? 【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。 【解答】均匀的各项异形体如:竹材,木材。 非均匀的各向同性体如:混凝土。 【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体? 【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。 【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。 【1-3】五个基本假定在建立弹性力学基本方程时有什么作用? 【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。 均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。 各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。 小变形假定:假定位移和变形是微小的。亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。这样在建立物体变形以后的平衡方程时,就可以方便的用变形以前的尺寸来代替变形
弹性理论习题及答案
第三章弹性理论 姓名班级学号考试时间:20分钟 一、单项选择题 1、点弹性和弧弹性之间()关系 A、有 B、没有 C、不确定 2、冰棒的需求价格弹性()药品的需求价格弹性 A、大于 B、小于 C、等于 D、大于或等于 3、供给弹性()点弹性和弧弹性的区分 A、有 B、没有 C、不确定 4、垂直的需求曲线是()弹性 A、完全有 B、富有 C、完全无 5、水平的供给曲线是()弹性 A、完全有 B、富有 C、完全无 6、一种商品价格下降,另外一种商品需求上升,则两种商品之间是()关系 A、互补品 B、替代品 C、正常品 D、劣品 7、在长期中,供给曲线更()弹性 A、缺乏 B、富有 C、不确定 D、依商品而定 8、容易被替代的商品,其需求弹性() A、大 B、小 C、不确定 二、多项选择题 1、弹性一般分为()弹性 A、供给 B、需求 C、价格 D、收入 2、利用价格需求弹性可以区分出() A、生活必须品 B、奢侈品 C、经济商品 D、免费物品 三、简答题 1、影响商品需求价格弹性的因素 2、需求价格弹性的五种情况
答案 一.单项选择题 2. A 二.多项选择题 三.简答题 1. 影响商品需求价格弹性的因素 (1). 必需品与奢侈品 一般地说,奢侈品需求对价格是有弹性的,而必需品则是缺乏弹性的。 (2). 相近替代品的可获得性 一般来说,相近替代品越多的商品越富有弹性。替代品多,消费者从这种商品转向购买其他商品较为容易,对商品价格更敏感(如,香烟)。 (3). 商品所划定范畴的大小 一般来说,如果某产品存在着很接近的替代品的数量愈多,其需求价格弹性愈大。 (4). 时间的长短 计算某种商品价格弹性系数所考虑的时间愈长,其系数会愈大。当某一商品价格上升时,消费者需要一段时间去寻找可以接受的替代品,因此,短期内对该商品的需求量变化不大,而长期内消费者更可能转向其他替代品,因此,该提价商品的需求量变化会更加明显些。 2. 需求价格弹性的五种情况 (1). 当e=0时,需求对价格是完全无弹性的,即需求量与价格无关。则需求曲线为一条垂直于x轴的直线。如,垄断价格;婚丧用品,特效药等接近于完全无弹性。 (2). 当e=1时,需求对价格为单位弹性,即价格变化的百分比与需求量变化的百分比相等。 (3). 当e=∞时,需求对价格是完全有弹性,即需求曲线为一条垂直于P轴的直线。如,银行以某一固定的价格收购黄金;实行保护价的农产品。 (4). 当e>1时,需求对价格富有弹性,即需求变化的幅度大于价格变化的幅度。如,奢侈品。 (5). 当e<1时,需求队价格缺乏弹性,即需求变化的幅度小于价格变化的幅度。如,生活必需品。
弹性力学简明教程(第四版)-习题解答
【2-9】【解答】图2-17: 上(y =0) 左(x =0) 右(x =b ) l -1 1 m -1 () x f s () 1g y h ρ+ () 1g y h ρ-+ () y f s 1gh ρ 代入公式(2-15)得 ①在主要边界上x=0,x=b 上精确满足应力边界条件: ()()100(),0;===-+=x xy x x g y h σρτ()()1b b (),0; ===-+=x xy x x g y h σρτ ②在小边界0y =上,能精确满足下列应力边界条件:() () ,0y xy y y gh σρτ===-= ③在小边界2y h =上,能精确满足下列位移边界条件:()()2 2 0,0 ====y h y h u v 这两个位移边界条件可以应用圣维南原理,改用三个积分的应力边界条件来代替,当板 厚=1δ时,可求得固定端约束反力分别为: 10,,0s N F F gh b M ρ==-= 由于2y h =为正面,故应力分量与面力分量同号,则有: ()()()22210000 0b y y h b y y h b xy y h dx gh b xdx dx σρστ===?=-???=???=?? ??? ⑵图2-18 ①上下主要边界y=-h/2,y=h/2上,应精确满足公式(2-15) l m x f (s) y f (s) 2h y =- 0 -1 0 q 2 h y = 1 -1q -/2()y y h q σ==-,-/2()0yx y h τ==,/2()0y y h σ==,/21()yx y h q τ==- ②在x =0的小边界上,应用圣维南原理,列出三个积分的应力边界条件:负面上应力
(完整)[2018年最新整理]弹性力学简明教程(第四版)-课后习题解答
【3-1】为什么在主要边界(大边界)上必须满足精确的应力边界条件式(2-15),而在小边界上可以应用圣维南原理,用三个积分的应力边界条件(即主矢量、主矩的条件)来代替?如果在主要边界上用三个积分的应力边界条件代替式(2-15),将会发生什么问题? 【解答】弹性力学问题属于数学物理方程中的边值问题,而要使边界条件完全得到满足,往往比较困难。这时,圣维南原理可为简化局部边界上的应力边界条件提供很大的方便。将物体一小部分边界上的面力换成分布不同,但静力等效的面力(主矢、主矩均相同),只影响近处的应力分布,对远处的应力影响可以忽略不计。如果在占边界绝大部分的主要边界上用三个积分的应力边界条件来代替精确的应力边界条件(公式2-15),就会影响大部分区域的应力分布,会使问题的解答精度不足。 【3-2】如果在某一应力边界问题中,除了一个小边界条件,平衡微分方程和其它的应力边界条件都已满足,试证:在最后的这个小边界上,三个积分的应力边界条件必然是自然满足的,固而可以不必校核。 【解答】区域内的每一微小单元均满足平衡条件,应力边界条件实质上是边界上微分体的平衡条件,即外力(面力)与内力(应力)的平衡条件。研究对象整体的外力是满足平衡条件的,其它应力边界条件也都满足,那么在最后的这个次要边界上,三个积分的应力边界条件是自然满足的,因而可以不必校核。 【3-3】如果某一应力边界问题中有m 个主要边界和n 个小边界,试问在主要边界和小边界上各应满足什么类型的应力边界条件,各有几个条件? 【解答】在m 个主要边界上,每个边界应有2个精确的应力边界条件,公式(2-15),共2m 个;在n 个次要边界上,如果能满足精确应力边界条件,则有2n 个;如果不能满足公式(2-15)的精确应力边界条件,则可以用三个静力等效的积分边界条件来代替2个精确应力边界条件,共3n 个。 【3-4】试考察应力函数3 ay Φ=在图3-8所示的矩形板和坐标系中能解决什么问题(体力不计)? 【解答】⑴相容条件: 不论系数a 取何值,应力函数3 ay Φ=总能满足应力函数表示的相容方程,式(2-25). ⑵求应力分量 当体力不计时,将应力函数Φ代入公式(2-24),得 6,0,0x y xy yx ay σσττ==== ⑶考察边界条件 上下边界上应力分量均为零,故上下边界上无面力.
弹性力学试题及标准答案
弹性力学与有限元分析复习题及其答案 一、填空题 1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。 2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。 3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。 4、物体受外力以后,其内部将发生内力,它的集度称为应力。与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。应力及其分量的量纲是L -1 MT -2 。 5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。 6、平面问题分为平面应力问题和平面应变问题。 7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa , =2σ0MPa ,=1α6135'ο。 8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512 MPa , =2σ-312 MPa ,=1α-37°57′。 9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa , =2σ-2052 MPa ,=1α-82°32′。 10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。 11、表示应力分量与体力分量之间关系的方程为平衡微分方程。 12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。分为位移边界条件、应力边界条件和混合边界条件。 13、按应力求解平面问题时常采用逆解法和半逆解法。 14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。其具体步骤分为单元分析和整体分析两部分。 15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。 16、每个单元的应变一般总是包含着两部分:一部分是与该单元中各点的位置坐标有关的,是各点不相同的,即所谓变量应变;另一部分是与位置坐标无关的,是各点相同的,即所谓常量应变。 17、为了能从有限单元法得出正确的解答,位移模式必须能反映单元的刚体位移和常量应变,还应当尽可能反映相邻单元的位移连续性。 18、为了使得单元内部的位移保持连续,必须把位移模式取为坐标的单值连续函数,为了使得相邻单元的位移保持连续,就不仅要使它们在公共结点处具有相同的位移时,也能在整个公共边界上具有相同的位移。 19、在有限单元法中,单元的形函数N i 在i 结点N i =1;在其他结点N i =0及∑N i =1。 20、为了提高有限单元法分析的精度,一般可以采用两种方法:一是将单元的尺寸减小,以便较好地反映位移和应力变化情况;二是采用包含更高次项的位移模式,使位移和应力的精度提高。
弹性力学简明教程_第四章_课后作业题答案
第四章 平面问题的极坐标解答 【4-8】 实心圆盘在r ρ=的周界上受有均布压力q 的作用,试导出其解答。 【解答】实心圆盘是轴对称的,可引用轴对称应力解答,教材中的式(4-11),即 2 2(12ln )2(32ln )20A B C A B C ρ?ρ? σρρσρρτ? =+++? ???=-+++?? ?? =?? (a) 首先,在圆盘的周界(r ρ=)上,有边界条件()=r q ρρσ=-,由此得 -q 2 (12ln )2A B C ρσρρ = +++= (b) 其次,在圆盘的圆心,当0ρ→时,式(a )中ρσ,?σ的第一、第二项均趋于无限大,这是不可能的。按照有限值条件(即,除了应力集中点以外,弹性体上的应力应为有限值。),当=0ρ时,必须有0A B ==。 把上述条件代入式(b )中,得 /2C q =-。 所以,得应力的解答为 -q 0ρ?ρ?σστ===。 【4-9】 半平面体表面受有均布水平力q ,试用应力函数 2(sin 2)ΦρB φC φ=+求解应力分量(图4-15)。 【解答】(1)相容条件: 将应力函数Φ代入相容方程40?Φ=,显然满足。 (2)由Φ求应力分量表达式 =-2sin 222sin 222cos 2B C B C B C ρ?ρ?σ?? σ??τ??+?? =+??=--??
(3)考察边界条件:注意本题有两个?面,即2 π ?=± ,分别为?±面。在?±面 上,应力符号以正面正向、负面负向为正。因此,有 2()0,??πσ=±= 得0C =; -q 2 (),ρ??πτ=±= 得2 q B =-。 将各系数代入应力分量表达式,得 sin 2sin 2cos 2q q q ρ?ρ?σ?σ?τ? ?=?? =-??=?? 【4-14】 设有内半径为r 而外半径为R 的圆筒受内压力q ,试求内半径和外半径的改 变量,并求圆筒厚度的改变量。 【解答】本题为轴对称问题,只有径向位移而无环向位移。当圆筒只受内压力q 的情况下,取应力分量表达式,教材中式(4-11),注意到B =0。 内外的应力边界条件要求 r r ()0,()0;(), ()0 R R q ρ?ρρ?ρρρρρττσσ=======-= 由表达式可见,前两个关于ρ?τ的条件是满足的,而后两个条件要求 r 2 22,20A C q A C R ?+=-??? ?+=??。 由上式解得 22 2 ,C () 2() 22 22 qr R qr A R -r R -r =-=。 (a) 把A ,B ,C 值代入轴对称应力状态下对应的位移分离,教材中式(4-12)。 ()()222211cos sin ,(R r )qr R u I K E ρμρμ??ρ?? =-++++??-? ? (b) sin cos 0u H I K ?ρ??=-+=。 (c) 式(c )中的ρ,?取任何值等式都成立,所以各自由项的系数为零
弹性力学习题
弹性力学习题 填空题 1。弹性力学是建立在连续性、完全弹性、均匀性、各项同性及小变形假定(假定形变和唯一是微小的)假定基础。 2。在平面应力问题中,其中应力分量不恒为零的有σx,σy,τxy=τyx。而在平面应变问题中,应变分量横为零的有?z,txz=tzx,tzy=tyz。两类问题的应力和应变位移都只是坐标x,y的函数,与z无关。 3。体力不计,两端受转向相反力偶作用的等截面质感扭转问题中,存在的应力有横截面上的切应力t,其余应力为0,其任一横截面在xy轴上的投影的形状相同,而只是转动一个角度a=kz。 4。相容方程是形变分量之间的变形协调方程,只有满足相容方程,才能保证位移分量的存在,实际位移值应包括u,v,w。 5。平面问题中,(a)已知一点的应力为61=62=6,那么任一方向的正应力6n为6。 tn为0。 6。空间问题一点的应力状态是由6个独立的应力分量决定的,分别是沿直角坐标系的正应力6x,6y,6z和切应力txy,txz,tyz。任一方向的正应力和切应力实际上是这些应力分量在该方向上的合成。 1。弹性力学是固体力学的一个分支,其基本任务是研究由于受外力作用或边界约束,温度改变等原因为发生的。 2。在平面应力问题中,应力分量为0的是6x,tzx,tzy,而在平面应变中,应力分量一般不为0的有6x,6y,6z,txy。计算两种状态的基本方程中,平衡威风方程和几何方程是一样的。
3。对轴对称问题,得出的位移公式却是非轴对称的,因为位移包含刚体位移分量,只有位移边界条件也是轴对称的,则位移才是轴对称的。 4。一点的应力状态由6个独立的应力分量决定的,分别是沿坐标面的正应力6x,6y,6z和切应力tzy,tyz,tzx。一点应变状态有6的独立的独立的应变分量决定的,分别沿坐标面的线应变?x,?y,?z,和切应变rxy,ryz,rzx。 5。弹性力学的基本做题方法有应力法,位移法。 6。平面问题中,艾里应力函数是在条件常体力下得到的,应满足区域内的相容方程。 简答题 1、简述弹性力学的基本假设,并说说建立弹性力学基本方程时分别用到哪些假设, a、连续性 2、完全弹性 3、均匀性 4、各向同性 5、小变形假设即形变和位移均是微小的平衡微分方程和几何方程:物体的连续性、均匀性、小变形物理方程:全部用到 2、简述弹性力学应力、应变、体力和面力的符号规定(可用文字说明)。正的切应力对应正的切应变吗, 应力:截面的外法线沿坐标轴正向,则此截面为正面,正面上的应力沿坐标轴正向为正、负向为负。相反,负面上的应力沿坐标轴负向为正、正向为负。 应变:线应变以伸长时为正、缩短时为负;切应变以直角变小时为正、变大时为负。体力:沿坐标轴正方向为正、沿坐标轴负方向为负。 面力:沿坐标轴正方向为正、沿坐标轴负方向为负。 正的切应力对应正的切应变。(图)τxy与τyx均为正的切应力,它们的作用是使DA与DB间的夹角有减小的趋势,而根据切应变定义,此时应变为正。 3、简述平面问题的几何方程是如何得到的, a、先求出一点沿坐标轴x、y的线应变ξx、ξy。
